第六章 特殊平行四边形 1 菱形的性质与判定 第2课时 菱形的判定(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 1 菱形的性质与判定 第2课时 菱形的判定(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
1 菱形的性质与判定
第2课时 菱形的判定
基 础 练
练点1 由对角线的关系判定菱形
1.如图,□ABCD的对角线 AC 和 BD 相交于点O,下列说法正确的是( )
A.若OB=OD,则□ABCD是菱形 B.若AC=BD,则 ABCD是菱形
C.若OA=OD,则 ABCD是菱形 D.若AC⊥BD,则□ABCD是菱形
(第1题) (第 2题)
2.如图,在 ABCD 中,点E,F分别在边 AD,BC 上,且DE=BF,则再添加一个条件:___________,可判定四边形AFCE是菱形.(只写一个即可)
3. 如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是____________.(只需写出一个条件即可)
(第3 题) (第4题)
练点2 由边的关系判定菱形
4.如图,在△ABC中, AB = AC,将△ABC 沿边 BC 翻折,得到的△DBC 与原△ABC 拼成四边形ABDC,则能直接判定四边形ABDC 是菱形的依据是( )
A.一组邻边相等的平行四边形是菱形 B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形 D.对角线互相垂直平分的四边形是菱形
5.如图,在平行四边形ABCD 中, AB =4,BC =6,将线段 AB水平向右平移 a个单位得到线段EF,若四边形ECDF 为菱形,则a的值为( )
A.1 B.2 C.3 D.4
纠易错 臆造菱形的判定方法导致出错
6.下列说法不正确的是( )
A. 四条边相等的四边形是菱形 B.对角线垂直的平行四边形是菱形
C. 对角线垂直且相等的四边形是菱形 D.邻边相等的平行四边形是菱形
提 升 练
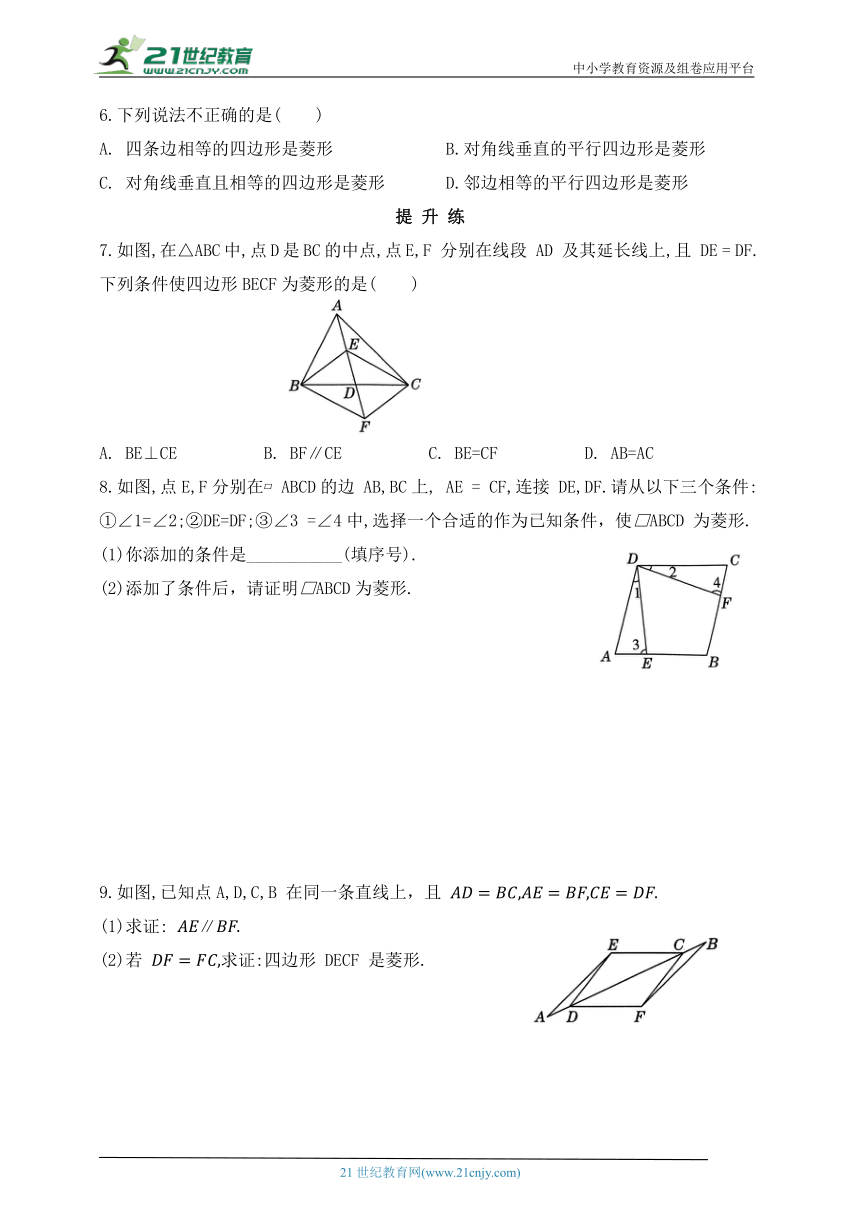
7.如图,在△ABC中,点D是BC的中点,点E,F 分别在线段 AD 及其延长线上,且 DE = DF.下列条件使四边形BECF为菱形的是( )
A. BE⊥CE B. BF∥CE C. BE=CF D. AB=AC
8.如图,点E,F分别在 ABCD的边 AB,BC上, AE = CF,连接 DE,DF.请从以下三个条件:
①∠1=∠2;②DE=DF;③∠3 =∠4中,选择一个合适的作为已知条件,使□ABCD 为菱形.
(1)你添加的条件是___________(填序号).
(2)添加了条件后,请证明□ABCD为菱形.
9.如图,已知点A,D,C,B 在同一条直线上,且
(1)求证: ∥
(2)若 求证:四边形 DECF 是菱形.
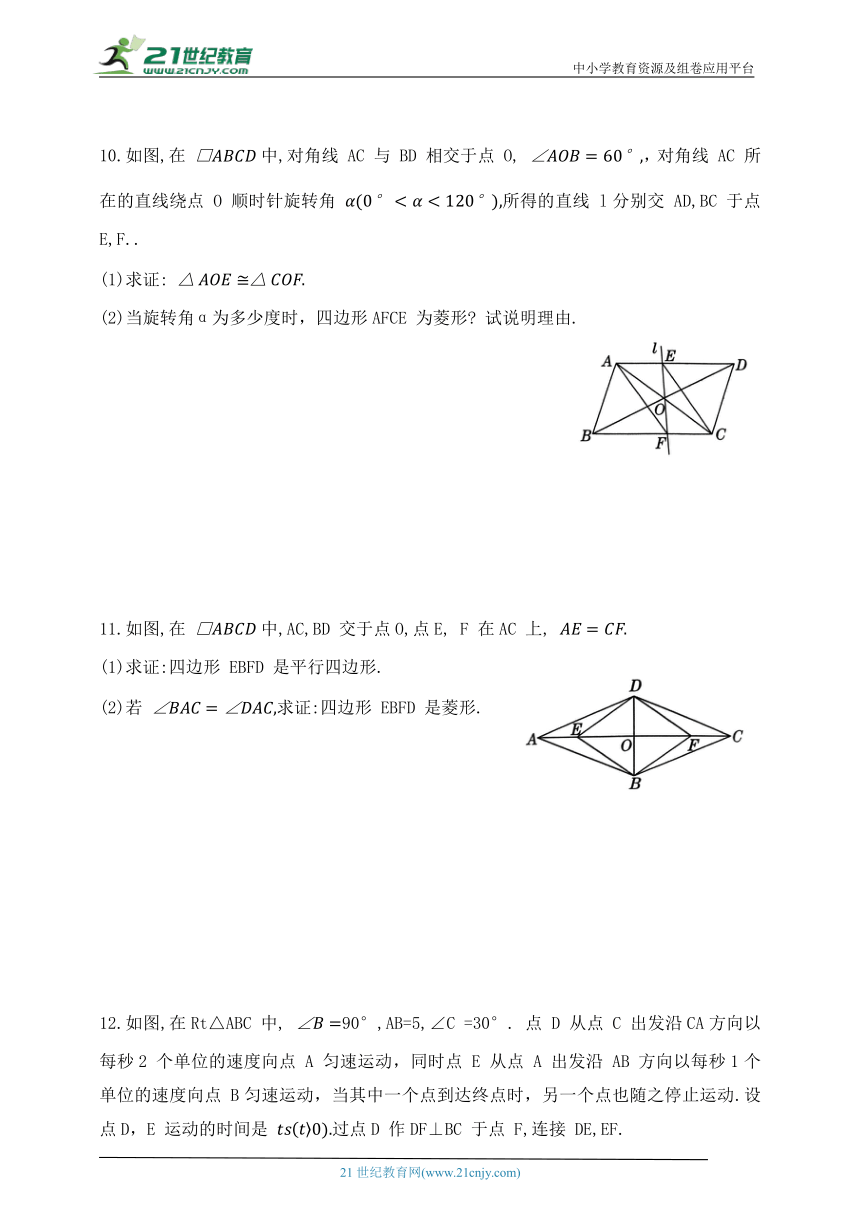
10.如图,在 中,对角线 AC 与 BD 相交于点 O, ,对角线 AC 所在的直线绕点 O 顺时针旋转角 所得的直线 l分别交 AD,BC 于点 E,F..
(1)求证:
(2)当旋转角α为多少度时,四边形AFCE 为菱形 试说明理由.
11.如图,在 中,AC,BD 交于点O,点E, F 在AC 上,
(1)求证:四边形 EBFD 是平行四边形.
(2)若 求证:四边形 EBFD 是菱形.
12.如图,在Rt△ABC 中, 90°,AB=5,∠C =30°. 点 D 从点 C 出发沿CA方向以每秒2 个单位的速度向点 A 匀速运动,同时点 E 从点 A 出发沿 AB 方向以每秒1个单位的速度向点 B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E 运动的时间是 过点D 作DF⊥BC 于点 F,连接 DE,EF.
(1)求证:四边形 AEFD 是平行四边形.
(2)四边形AEFD能够成为菱形吗 如果能,求出相应的 t值;如果不能,说明理由.
参考答案
(答案不唯一) (答案不唯一)
4. B 【点拨】由翻折的性质可得
因为 所以 所以根据“四边相等的四边形是菱形”可得四边形ABDC 是菱形.
5. B 【点拨】∵四边形ABCD 是平行四边形, ∥CD,CE∥FD,CD=AB=4.
∵将线段AB 水平向右平移得到线段EF,∴AB∥EF∥CD,∴四边形ECDF为平行四边形.
∴ 当 CD= CE=4时,□ECDF 为菱形,此时a =BE=BC-CE=6-4=2.
6. C
7. D 【点拨】∵AB =AC,点D是 BC 的中点,∴EF⊥BC,BD=DC.
∵ DE=DF,∴ 四边形BECF 是平行四边形.
∵ EF⊥BC,∴ 四边形BECF 是菱形. 选项 A,B,C 的条件都不能推出四边形BECF是菱形,只有选项 D 正确.
8.(1)①
(2)【证明】∵四边形ABCD 是平行四边形,∴∠A =∠C.
在△ADE 和△CDF 中 ∴△ADE≌△CDF(AAS),∴AD=CD,
∴□ABCD为菱形.
【点拨】本题答案不唯一.
9.【证明】(1)∵AD=BC,∴AD+CD=BC+CD,∴AC=BD.
∵AE=BF,CE =DF,∴△AEC≌△BFD(SSS), ∴∠A=∠B,∴AE∥BF.
(2)∵△AEC≌△BFD,∴ ∠ECA=∠FDB,∴ EC∥DF.
∵ EC = DF,∴ 四边形 DECF 是平行四边形.
∵DF=FC,∴四边形DECF 是菱形.
10.(1)【证明】∵ 四边形ABCD 是平行四边形,∴AD∥BC,AO = CO.∴ ∠AEO =∠CFO.
又∵ ∠AOE=∠COF,∴△AOE≌COF(AAS).
(2)【解】当α=90°时,四边形 AFCE 为菱形.理由:
∵△AOE≌△COF,∴ OE =OF.又∵AO=CO,∴四边形 AFCE 为平行四边形.
又∵α=90°,即∠AOE=90°,∴AC⊥EF.∴四边形AFCE为菱形.
11.【证明】(1)在 ABCD中,OA =OC,OB=OD.
∵AE=CF,∴OE=OF,∴四边形EBFD是平行四边形.
(2)∵四边形ABCD 是平行四边形,∴AB∥DC,∴∠BAC=∠DCA.
∵∠BAC=∠DAC,∴ ∠DCA=∠DAC,∴ DA = DC,∴ ABCD 为菱形,
∴DB⊥EF,∴□EBFD是菱形.
12.(1)【证明】∵∠B =90°,∴AB⊥BC.
又∵DF⊥BC,∴AE∥DF.
由题意得 AE =t,DC = 2t,∵ 在△DFC中,
DC =t,∴AE=DF.∴四边形AEFD 是平行四边形.
(2)【解】能.理由:由(1)知四边形 AEFD 是平行四边形.
∵∠C=30°,∠B=90°,∴AC=2AB=2×5=10,∴ AD=AC-DC = 10-2t.
若□AEFD 为菱形,则需AE=AD,即t =10-2t,解得
即当时,四边形AEFD为菱形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
1 菱形的性质与判定
第2课时 菱形的判定
基 础 练
练点1 由对角线的关系判定菱形
1.如图,□ABCD的对角线 AC 和 BD 相交于点O,下列说法正确的是( )
A.若OB=OD,则□ABCD是菱形 B.若AC=BD,则 ABCD是菱形
C.若OA=OD,则 ABCD是菱形 D.若AC⊥BD,则□ABCD是菱形
(第1题) (第 2题)
2.如图,在 ABCD 中,点E,F分别在边 AD,BC 上,且DE=BF,则再添加一个条件:___________,可判定四边形AFCE是菱形.(只写一个即可)
3. 如图,在四边形ABCD中,AC⊥BD,垂足为O,AB∥CD,要使四边形ABCD为菱形,应添加的条件是____________.(只需写出一个条件即可)
(第3 题) (第4题)
练点2 由边的关系判定菱形
4.如图,在△ABC中, AB = AC,将△ABC 沿边 BC 翻折,得到的△DBC 与原△ABC 拼成四边形ABDC,则能直接判定四边形ABDC 是菱形的依据是( )
A.一组邻边相等的平行四边形是菱形 B.四边相等的四边形是菱形
C.对角线互相垂直的平行四边形是菱形 D.对角线互相垂直平分的四边形是菱形
5.如图,在平行四边形ABCD 中, AB =4,BC =6,将线段 AB水平向右平移 a个单位得到线段EF,若四边形ECDF 为菱形,则a的值为( )
A.1 B.2 C.3 D.4
纠易错 臆造菱形的判定方法导致出错
6.下列说法不正确的是( )
A. 四条边相等的四边形是菱形 B.对角线垂直的平行四边形是菱形
C. 对角线垂直且相等的四边形是菱形 D.邻边相等的平行四边形是菱形
提 升 练
7.如图,在△ABC中,点D是BC的中点,点E,F 分别在线段 AD 及其延长线上,且 DE = DF.下列条件使四边形BECF为菱形的是( )
A. BE⊥CE B. BF∥CE C. BE=CF D. AB=AC
8.如图,点E,F分别在 ABCD的边 AB,BC上, AE = CF,连接 DE,DF.请从以下三个条件:
①∠1=∠2;②DE=DF;③∠3 =∠4中,选择一个合适的作为已知条件,使□ABCD 为菱形.
(1)你添加的条件是___________(填序号).
(2)添加了条件后,请证明□ABCD为菱形.
9.如图,已知点A,D,C,B 在同一条直线上,且
(1)求证: ∥
(2)若 求证:四边形 DECF 是菱形.
10.如图,在 中,对角线 AC 与 BD 相交于点 O, ,对角线 AC 所在的直线绕点 O 顺时针旋转角 所得的直线 l分别交 AD,BC 于点 E,F..
(1)求证:
(2)当旋转角α为多少度时,四边形AFCE 为菱形 试说明理由.
11.如图,在 中,AC,BD 交于点O,点E, F 在AC 上,
(1)求证:四边形 EBFD 是平行四边形.
(2)若 求证:四边形 EBFD 是菱形.
12.如图,在Rt△ABC 中, 90°,AB=5,∠C =30°. 点 D 从点 C 出发沿CA方向以每秒2 个单位的速度向点 A 匀速运动,同时点 E 从点 A 出发沿 AB 方向以每秒1个单位的速度向点 B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E 运动的时间是 过点D 作DF⊥BC 于点 F,连接 DE,EF.
(1)求证:四边形 AEFD 是平行四边形.
(2)四边形AEFD能够成为菱形吗 如果能,求出相应的 t值;如果不能,说明理由.
参考答案
(答案不唯一) (答案不唯一)
4. B 【点拨】由翻折的性质可得
因为 所以 所以根据“四边相等的四边形是菱形”可得四边形ABDC 是菱形.
5. B 【点拨】∵四边形ABCD 是平行四边形, ∥CD,CE∥FD,CD=AB=4.
∵将线段AB 水平向右平移得到线段EF,∴AB∥EF∥CD,∴四边形ECDF为平行四边形.
∴ 当 CD= CE=4时,□ECDF 为菱形,此时a =BE=BC-CE=6-4=2.
6. C
7. D 【点拨】∵AB =AC,点D是 BC 的中点,∴EF⊥BC,BD=DC.
∵ DE=DF,∴ 四边形BECF 是平行四边形.
∵ EF⊥BC,∴ 四边形BECF 是菱形. 选项 A,B,C 的条件都不能推出四边形BECF是菱形,只有选项 D 正确.
8.(1)①
(2)【证明】∵四边形ABCD 是平行四边形,∴∠A =∠C.
在△ADE 和△CDF 中 ∴△ADE≌△CDF(AAS),∴AD=CD,
∴□ABCD为菱形.
【点拨】本题答案不唯一.
9.【证明】(1)∵AD=BC,∴AD+CD=BC+CD,∴AC=BD.
∵AE=BF,CE =DF,∴△AEC≌△BFD(SSS), ∴∠A=∠B,∴AE∥BF.
(2)∵△AEC≌△BFD,∴ ∠ECA=∠FDB,∴ EC∥DF.
∵ EC = DF,∴ 四边形 DECF 是平行四边形.
∵DF=FC,∴四边形DECF 是菱形.
10.(1)【证明】∵ 四边形ABCD 是平行四边形,∴AD∥BC,AO = CO.∴ ∠AEO =∠CFO.
又∵ ∠AOE=∠COF,∴△AOE≌COF(AAS).
(2)【解】当α=90°时,四边形 AFCE 为菱形.理由:
∵△AOE≌△COF,∴ OE =OF.又∵AO=CO,∴四边形 AFCE 为平行四边形.
又∵α=90°,即∠AOE=90°,∴AC⊥EF.∴四边形AFCE为菱形.
11.【证明】(1)在 ABCD中,OA =OC,OB=OD.
∵AE=CF,∴OE=OF,∴四边形EBFD是平行四边形.
(2)∵四边形ABCD 是平行四边形,∴AB∥DC,∴∠BAC=∠DCA.
∵∠BAC=∠DAC,∴ ∠DCA=∠DAC,∴ DA = DC,∴ ABCD 为菱形,
∴DB⊥EF,∴□EBFD是菱形.
12.(1)【证明】∵∠B =90°,∴AB⊥BC.
又∵DF⊥BC,∴AE∥DF.
由题意得 AE =t,DC = 2t,∵ 在△DFC中,
DC =t,∴AE=DF.∴四边形AEFD 是平行四边形.
(2)【解】能.理由:由(1)知四边形 AEFD 是平行四边形.
∵∠C=30°,∠B=90°,∴AC=2AB=2×5=10,∴ AD=AC-DC = 10-2t.
若□AEFD 为菱形,则需AE=AD,即t =10-2t,解得
即当时,四边形AEFD为菱形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
