2022~2023学年黑龙江齐齐哈尔龙沙区恒昌中学高二上学期期中数学试卷(PDF版含解析)
文档属性
| 名称 | 2022~2023学年黑龙江齐齐哈尔龙沙区恒昌中学高二上学期期中数学试卷(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 08:48:28 | ||
图片预览



文档简介
2022~2023学年黑龙江齐齐哈尔龙沙区恒昌中学高二上学期期中数学试卷
一、单选题(本大题共8小题,每小题5分,共40分)
1、椭圆 上点 到上焦点的距离为4,则点 到下焦点的距离为( )
A.6
B.3
C.4
D.2
2、直线l的一个方向向量为 ,平面 的一个法向量为 ,若 ,则实数 ( )
A.
B.1
C.
D.
3、直线 恒过定点( )
A.
B.
C.
D.
4、唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的
数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样
走才能使总路程最短?在平面直角坐标系中,设军营所在的位置为 ,若将军从山脚下的点 处出
发,河岸线所在直线l的方程为 ,则“将军饮马”的最短总路程是( )
A.
B.
C.
D.
5、已知圆 ,则圆上的点到坐标原点的距离的最大值为( )
A.
B.
C.
D.
6、如图所示,在四面体 中, , , ,点 在 上,且 , 为 的中点,则
( )
A.
B.
C.
D.
7、如图为陕西博物馆收藏的国宝——唐 金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代
金银细作的典范之作.该杯的主体部分可以近似看作是双曲线 1(a>0,b>0)的右支与y轴及平行
于x轴的两条直线围成的曲边四边形ABMN绕y轴旋转一周得到的几何体,若该金杯主体部分的上口外直径为
,下底座外直径为 ,且杯身最细之处到上杯口的距离是到下底座距离的2倍,则杯身最细之处的周
长为( )
A.2 π
B.3π
C.2 π
D.4π
8、已知双曲线 的左焦点为 ,以 为直径的圆与双曲线 的渐近线交于不
同原点 的 , 两点,若四边形 的面积为 ,则双曲线 的渐近线方程为
A.
B.
C.
D.
二、多选题(本大题共4小题,每小题5分,共20分)
9、下列说法中,正确的有( )
A.直线 必过定点
B.直线 在 轴上的截距为1
C.直线 的倾斜角为
D.点 到直线 的距离为1
10、圆 和圆 的交点为A,B,则( )
A.公共弦AB所在直线的方程为
B.线段AB中垂线方程为
C.公共弦AB的长为
D.P为圆 上一动点,则P到直线AB距离的最大值为
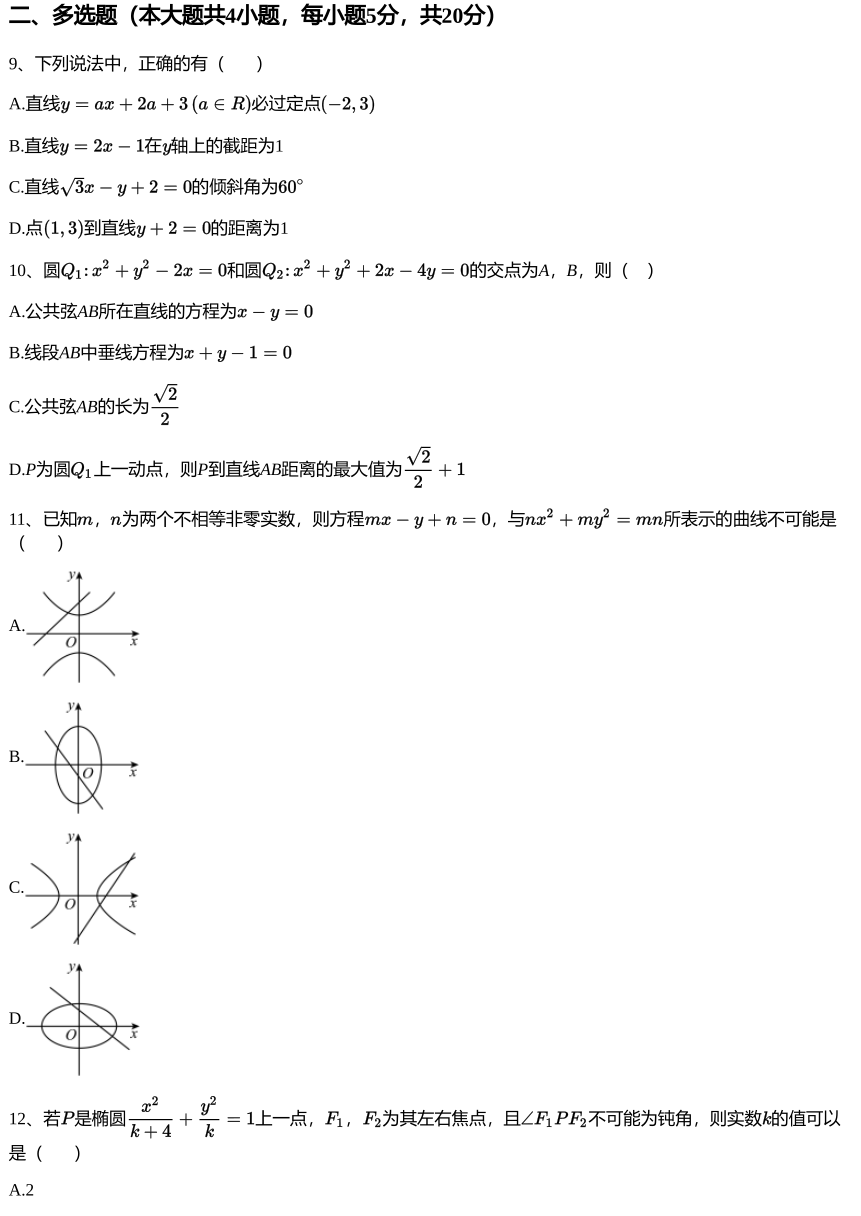
11、已知 , 为两个不相等非零实数,则方程 ,与 所表示的曲线不可能是
( )
A.
B.
C.
D.
12、若 是椭圆 上一点, , 为其左右焦点,且 不可能为钝角,则实数 的值可以
是( )
A.2
B.3
C.4
D.5
三、填空题(本大题共4小题,每小题5分,共20分)
13、明朝的一个葡萄纹椭圆盘如图1所示,清朝的一个青花山水楼阁纹椭圆盘如图2所示,北宋的一个汝窑椭圆
盘如图3所示,这三个椭圆盘的外轮廓均为椭圆,已知图(1)、图(2)、图(3)中椭圆的长轴长、短轴长的
比值分别为 、 、 ,则对应的椭圆盘最圆的是图 (填序号)
14、与椭圆 有公共焦点,且离心率为 的双曲线方程为 .
15、已知椭圆 ,过 , 点作直线 交椭圆 于 , 两点,且点 是 的中点,则直线 的方程
是 .
16、已知斜率为 的直线 经过双曲线 的上焦点 ,且与双曲线的上、下两支都相交,则双曲线的
离心率 的取值范围是 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
已知 的三个顶点的坐标分别为 , , .
(1)求 边上中线 所在直线的方程;
(2)求 边上高 所在直线的方程.
18、(本小题12分)
如图,在棱长为2的正方体 中,E为 的中点.
(1)求证: 平面 ;
(2)求直线 与平面 所成角的正弦值;
(3)求点C到平面 的距离.
19、(本小题12分)
已知圆
(1)若直线 过点 ,且与圆 相切,求直线 的方程;
(2)若圆 的半径为3,圆心在直线 上,且与圆 外切,求圆 的方程.
20、(本小题12分)
已知椭圆 : 的下焦点为 、上焦点为 ,其离心率 .过焦点 且与x轴不垂直的直线l交
椭圆于A、B两点.
(1)求实数m的值;
(2)求△ABO(O为原点)面积的最大值.
21、(本小题12分)
如图所示,在四棱锥 中,平面 平面 , 为等边三角形, ,
, ,点 是 的中点,
(1)求平面 与平面 夹角的余弦值;
(2)在线段 上是否存在一点 ,使得 平面 ?若存在,求出 的值;若不存在,请说明理由.
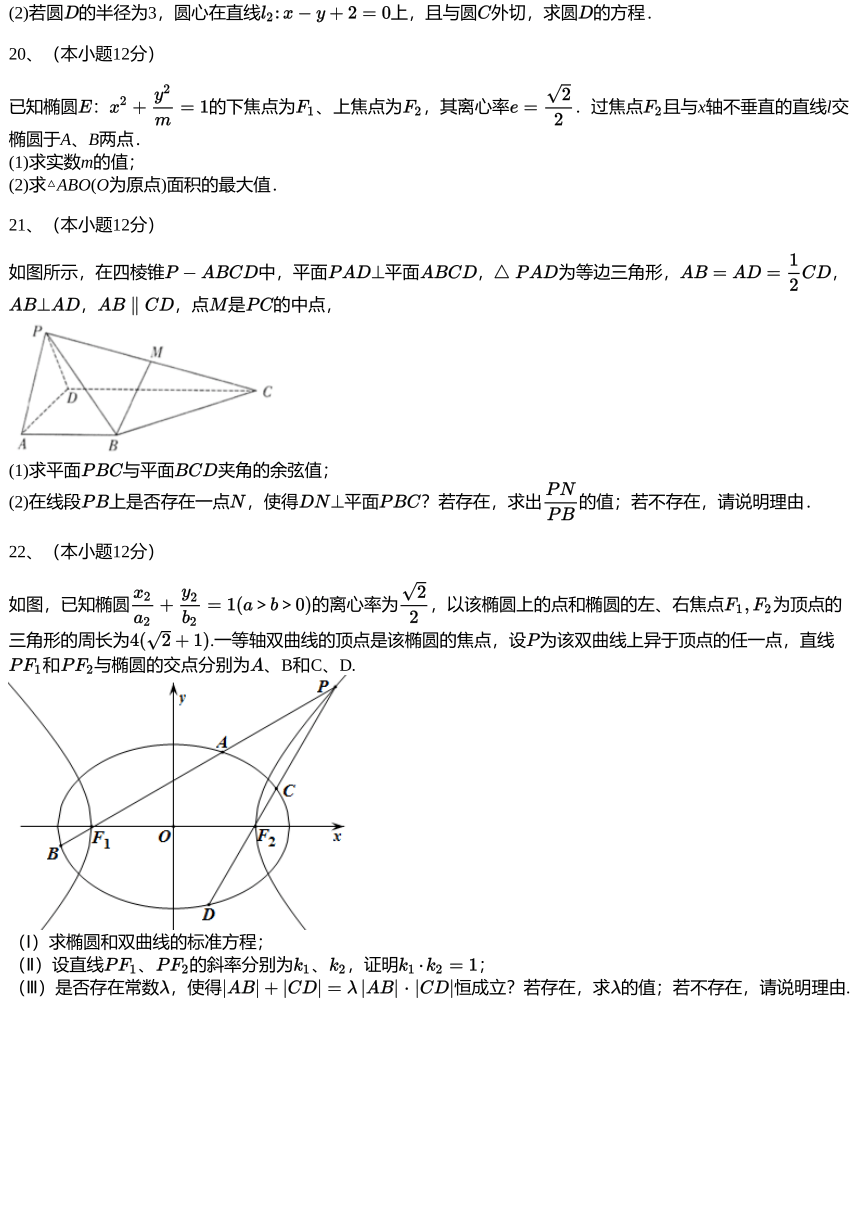
22、(本小题12分)
如图,已知椭圆 > > 的离心率为 ,以该椭圆上的点和椭圆的左、右焦点 为顶点的
三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设 为该双曲线上异于顶点的任一点,直线
和 与椭圆的交点分别为 、B和C、D.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线 、 的斜率分别为 、 ,证明 ;
(Ⅲ)是否存在常数 ,使得 恒成立?若存在,求 的值;若不存在,请说明理由.
参考答案
一、单选题
1、
【答案】
A
【分析】
根据椭圆方程求出 ,再根据椭圆的定义计算可得;
【详解】
解:椭圆 ,所以 ,即 ,设上焦点为 ,下焦点为 ,则
,因为 ,所以 ,即点 到下焦点的距离为 ;
故选:A
2、
【答案】
A
【分析】
由题意可知,直线 的方向向量与平面 的法向量平行,由此即可求出结果.
【详解】
直线l的一个方向向量为 ,平面 的一个法向量为 ,且 ,
所以 ,
所以 .
故选:A.
3、
【答案】
A
【分析】
将直线变形为 ,由 且 ,即可求出定点.
【详解】
将 变形为: ,令 且 ,解得
, ,
所以直线恒过定点 .
故选:A
4、
【答案】
D
【分析】
先求点 关于直线 对称的点 ,再根据两点之间线段最短,即可得解.
【详解】
如图,设 关于直线 对称的点为 ,
则有 ,可得 ,可得 ,
依题意可得“将军饮马”的最短总路程为 ,
此时 ,
故选:D.
5、
【答案】
D
【分析】
由圆的方程可确定圆心和半径,根据圆上点到定点距离最大值为 可求得结果.
【详解】
由 得: , 圆心 ,半径 ,
圆心到坐标原点的距离 ,
圆上的点到坐标原点的距离的最大值为 .
故选:D.
【点睛】
结论点睛:若圆心到圆外定点的距离为 ,半径为 ,则圆上的点到圆外定点距离的最大值为 ,最小值为
.
6、
【答案】
B
【分析】
解:通过题意分析可以得,连接 ,画图如下:
是 的中点,
,
,
,
.
因此正确答案为:B
7、
【答案】
C
【分析】
该金杯主体部分的上口外直径为 ,下底座外直径为 ,
且杯身最细之处到上杯口的距离是到下底座距离的2倍,
可设 代入双曲线方程可得
,
即 ,
作差可得 ,解得 ,
所以杯身最细处的周长为 .
因此正确答案为:C
8、
【答案】
C
【分析】
通过题意, ,双曲线 的焦点 到 的一条渐近线 的距离为 ,则 ,所
以 ,所以 ,所以 ,所以双曲线 的渐近线方程为 .
二、多选题
9、
【答案】
A;C
【分析】
对A,化简方程令 的系数为0求解即可.
对B,根据截距的定义辨析即可.
对C,求出直线的斜率再根据斜率与倾斜角的关系辨析即可.
对D,利用横纵坐标的差求解即可.
【详解】
对A,化简得直线 ,故定点为 .故A正确.
对B, 在 轴上的截距为 .故B错误.
对C,直线 的斜率为 ,故倾斜角 满足 , , ,
即 .故C正确.
对D, 因为直线 垂直于 轴,故 到 的距离为 .故D错误.
故选:AC.
10、
【答案】
A;B;D
【分析】
两圆方程作差后可得公共弦方程,从而可判断A的正误,求出圆 的圆心坐标后求出垂直平分线的方程后可判
断B的正误,利用垂径定理计算弦长后可判断C的正误,求出 到直线的距离后可求动点到直线距离的最大值,
从而可判断D的正误.
【详解】
对于选项A,因为圆 : , : ,
两式作差可得公共弦AB所在直线的方程为 ,即 ,故A正确;
对于选项B,圆 : 的圆心为 ,
则线段AB中垂线的斜率为 ,即线段AB中垂线方程为 ,
整理可得 ,故B正确;
对于选项C,圆心 到 的距离为 ,
又圆 的半径 ,所以 ,故C不正确;
对于选项D,P为圆 上一动点,圆心 到 的距离为 ,
又圆 的半径 ,所以P到直线AB距离的最大值为 ,故D正确.
故选:ABD.
11、
【答案】
A;B;D
【分析】
先变形得到 ,对四个选项一一分析,得到答案.
【详解】
变形得到 ,
A选项,双曲线交点在 轴上,故 ,
此时 应该经过第一,二,四象限,A不可能;
B选项,椭圆焦点在 轴上,故 ,
此时 经过第一,二,三象限,B不可能;
C选项,双曲线交点在 轴上,故 ,
此时 应该经过第一,三,四象限,C可能;
D选项,椭圆焦点在 轴上,故 ,
此时 经过第一,二,三象限,D不可能;
故选:ABD
12、
【答案】
C;D
【分析】
根据椭圆的几何性质可判断 为椭圆的短轴端点时,此时 最大,即可列不等式求解.
【详解】
由椭圆的性质可得当点 为椭圆的短轴端点时,此时 最大,
若 不可能为钝角,当点 为椭圆的短轴断点时,则 ,
则 ,即 ,
又焦点在 轴上 ,解得 ,
所以实数 的值可以是4,5,
故选:CD
三、填空题
13、
【答案】
(2)
【分析】
由椭圆的离心率大小即可求解椭圆的扁平程度.
【详解】
设椭圆方程的长半轴长与短半轴长分别为 , ,
则椭圆的离心率 ,
显然 越大, 越小,
由于三个椭圆的 分别为 ,且
又 则 ,
故椭圆盘(2)的离心率最小,故椭圆盘(2)最圆.
故答案为:(2)
14、
【答案】
【分析】
由椭圆方程求出焦点坐标,得出 的值,再由双曲线的离心率得出 ,进而可得双曲线的标准方程.
【详解】
由椭圆方程 ,可得焦点为
设双曲线的半焦距为 ,则 ,因双曲线的离心率为 ,则
故 ,所以 ,
所以双曲线的标准方程为:
故答案为:
15、
【答案】
【分析】
设 ,结合中点公式和“点差法”求得直线 的斜率,结合直线的点斜式方程,即可求解.
【详解】
设 ,
因为点 , 是 的中点,可得 ,
由 ,两式相减得 ,
即 ,所以直线 的方程为 ,即 .
故答案为: .
16、
【答案】
【分析】
根据已知直线的斜率,求出渐近线的斜率范围,推出 , 的关系,然后求出离心率的范围.
【详解】
由题意可得双曲线的渐近线方程为 ,
过双曲线上焦点 且平行于渐近线 的方程为 ,此直线与只与双曲线的上支有一个交点,要使
斜率为 的直线 经过双曲线的上焦点 的直线 与与双曲线的上、下两支相交,则 ,所以
,因此 ,
故答案为:
四、解答题
17、
【答案】
(1) ;(2) .
【分析】
(1) 中点为 , ,
直线 方程为: ,即 ;
(2) , ,
直线 方程为: ,即 .
18、
【答案】
(1)证明见解析;
(2) ;
(3)2.
【分析】
(1)在正方体 中, ,则四边形 为平行
四边形,
因此 ,而 平面 , 平面 ,
所以 平面 .
(2)在棱长为2的正方体 中,射线 两两垂直,以点A为原点建立如下图所
示的空间直角坐标系,
,棱 的中点 ,
,
设平面 的法向量 ,则 ,令 ,得
,
直线 与平面 所成的角为 ,则 ,
所以直线 与平面 所成角的正弦值为 .
(3)由(2)知, ,
所以点C到平面 的距离 .
19、
【答案】
(1) ,
(2) 或
【分析】
(1)根据题意,可分直线 的斜率不存在和存在两种情况讨论,结合直线与圆相切,利用点到直线的距离公
式,列出方程,即可求解;
(2)设 ,由两圆相外切,得到 ,列出方程求得 的值,即可求解.
【详解】
(1)解:由圆 ,可得原心 ,半径为 ,
当直线 的斜率不存在时,直线方程为 ,此时直线与圆相切,符合题意;
当直线 的斜率存在时,设直线 的方程为 ,即 ,
由圆心 到直线 的距离等于半径,可得 ,解得 ,
此时直线 的方程为 ,
综上可得,所求直线的方程为 或 .
(2)解:由圆 的半径为3,圆心在直线 上,
设 ,且圆 的圆心 ,半径为 ,
由两圆相外切,可得 ,即 ,
解得 或 ,所以 或 ,
所以所求圆的方程为 或 .
20、
【答案】
(1)2;
(2) ﹒
【分析】
(1)根据已知条件得 , ,结合离心率 ,即可解得答案.
(2)设直线的方程,与椭圆方程联立,利用弦长公式以及三角形的面积公式,基本不等式即可得出答案.
【详解】
(1)由题意可得, , ,
∵离心率 ,
∴ ,
∵ ,
∴ ,解得 .
(2)由(1)知,椭圆 ,上焦点 ,
设 , , , ,直线 的方程为: ,
联立 ,得 ,
∴ , ,
∴ ,
∴ ,
∴
,
当且仅当 ,即 时等号成立,
∴ 为原点)面积的最大值为 .
21、
【答案】
(1)
(2)不存在,理由见解析
【分析】
(1)建立空间直角坐标系,利用法向量的夹角求解即可,
(2)利用线面垂直的向量关系即可求解.
【详解】
(1)证明:取 中点 ,连接 .因为 ,所以 .
因为平面 平面 ,平面 平面 , 平面 ,
所以 平面 .取 中点 ,连接 ,则 .
以 为原点,如图建立空间直角坐标系,设 ,
则 , , , , , , .
平面 的法向量 ,设平面 的法向量 ,
由 ,得
令 ,则 .
所以 ,
所以平面 与平面 夹角的余弦值 ;
(2)在线段 上是不存在点 ,使得 平面 .
设点 ,且 , ,则 ,
所以 .
则 所以 , .
若 平面 ,则 ,即 ,此方程无解,
所以在线段 上不存在点 ,使得 平面 .
22、
【答案】
(Ⅰ)椭圆的标准方程为 ;双曲线的标准方程为
(Ⅱ) =1.(Ⅲ)存在常数 使得 恒成立,
【分析】
试题分析:(1)设椭圆的半焦距为c,通过题意知: ,
2a+2c=4( +1),所以a=2 ,c=2.
又a2=b2+c2,因此b=2.故椭圆的标准方程为 =1.
通过题意设等轴双曲线的标准方程为 =1(m>0),因为等轴双曲线的顶点是椭圆的焦点,所以m=2,
因此双曲线的标准方程为 =1.
(2)设A(x1,y1),B(x2,y2),P(x0,y0),则k1= ,k2= .
因为点P在双曲线x2-y2=4上,所以x-y=4.
因此k1·k2= · = =1,即k1·k2=1.
(3)由于PF1的方程为y=k1(x+2),将其代入椭圆方程得(2k +1)x
2-8k x+8k -8=0,
显然2k +1≠0,显然Δ>0.由韦达定理得x1+x2= ,x1x2= .
所以|AB|=
= .
同理可知|CD|= .
则 ,
又k1·k2=1,
所以 .
故|AB|+|CD|= |AB|·|CD|.
因此存在λ= ,使|AB|+|CD|=λ|AB|·|CD|恒成立.
考点:本题考查了圆锥曲线方程的求法及直线与圆锥曲线的位置关系
点评:对于直线与圆锥曲线的综合问题,往往要联立方程,同时结合一元二次方程根与系数的关系进行求解;
而对于最值问题,则可将该表达式用直线斜率k表示,然后通过题意将其进行化简结合表达式的形式选取最值的
计算方式
一、单选题(本大题共8小题,每小题5分,共40分)
1、椭圆 上点 到上焦点的距离为4,则点 到下焦点的距离为( )
A.6
B.3
C.4
D.2
2、直线l的一个方向向量为 ,平面 的一个法向量为 ,若 ,则实数 ( )
A.
B.1
C.
D.
3、直线 恒过定点( )
A.
B.
C.
D.
4、唐代诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的
数学问题——“将军饮马”问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样
走才能使总路程最短?在平面直角坐标系中,设军营所在的位置为 ,若将军从山脚下的点 处出
发,河岸线所在直线l的方程为 ,则“将军饮马”的最短总路程是( )
A.
B.
C.
D.
5、已知圆 ,则圆上的点到坐标原点的距离的最大值为( )
A.
B.
C.
D.
6、如图所示,在四面体 中, , , ,点 在 上,且 , 为 的中点,则
( )
A.
B.
C.
D.
7、如图为陕西博物馆收藏的国宝——唐 金筐宝钿团花纹金杯,杯身曲线内收,玲珑娇美,巧夺天工,是唐代
金银细作的典范之作.该杯的主体部分可以近似看作是双曲线 1(a>0,b>0)的右支与y轴及平行
于x轴的两条直线围成的曲边四边形ABMN绕y轴旋转一周得到的几何体,若该金杯主体部分的上口外直径为
,下底座外直径为 ,且杯身最细之处到上杯口的距离是到下底座距离的2倍,则杯身最细之处的周
长为( )
A.2 π
B.3π
C.2 π
D.4π
8、已知双曲线 的左焦点为 ,以 为直径的圆与双曲线 的渐近线交于不
同原点 的 , 两点,若四边形 的面积为 ,则双曲线 的渐近线方程为
A.
B.
C.
D.
二、多选题(本大题共4小题,每小题5分,共20分)
9、下列说法中,正确的有( )
A.直线 必过定点
B.直线 在 轴上的截距为1
C.直线 的倾斜角为
D.点 到直线 的距离为1
10、圆 和圆 的交点为A,B,则( )
A.公共弦AB所在直线的方程为
B.线段AB中垂线方程为
C.公共弦AB的长为
D.P为圆 上一动点,则P到直线AB距离的最大值为
11、已知 , 为两个不相等非零实数,则方程 ,与 所表示的曲线不可能是
( )
A.
B.
C.
D.
12、若 是椭圆 上一点, , 为其左右焦点,且 不可能为钝角,则实数 的值可以
是( )
A.2
B.3
C.4
D.5
三、填空题(本大题共4小题,每小题5分,共20分)
13、明朝的一个葡萄纹椭圆盘如图1所示,清朝的一个青花山水楼阁纹椭圆盘如图2所示,北宋的一个汝窑椭圆
盘如图3所示,这三个椭圆盘的外轮廓均为椭圆,已知图(1)、图(2)、图(3)中椭圆的长轴长、短轴长的
比值分别为 、 、 ,则对应的椭圆盘最圆的是图 (填序号)
14、与椭圆 有公共焦点,且离心率为 的双曲线方程为 .
15、已知椭圆 ,过 , 点作直线 交椭圆 于 , 两点,且点 是 的中点,则直线 的方程
是 .
16、已知斜率为 的直线 经过双曲线 的上焦点 ,且与双曲线的上、下两支都相交,则双曲线的
离心率 的取值范围是 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
已知 的三个顶点的坐标分别为 , , .
(1)求 边上中线 所在直线的方程;
(2)求 边上高 所在直线的方程.
18、(本小题12分)
如图,在棱长为2的正方体 中,E为 的中点.
(1)求证: 平面 ;
(2)求直线 与平面 所成角的正弦值;
(3)求点C到平面 的距离.
19、(本小题12分)
已知圆
(1)若直线 过点 ,且与圆 相切,求直线 的方程;
(2)若圆 的半径为3,圆心在直线 上,且与圆 外切,求圆 的方程.
20、(本小题12分)
已知椭圆 : 的下焦点为 、上焦点为 ,其离心率 .过焦点 且与x轴不垂直的直线l交
椭圆于A、B两点.
(1)求实数m的值;
(2)求△ABO(O为原点)面积的最大值.
21、(本小题12分)
如图所示,在四棱锥 中,平面 平面 , 为等边三角形, ,
, ,点 是 的中点,
(1)求平面 与平面 夹角的余弦值;
(2)在线段 上是否存在一点 ,使得 平面 ?若存在,求出 的值;若不存在,请说明理由.
22、(本小题12分)
如图,已知椭圆 > > 的离心率为 ,以该椭圆上的点和椭圆的左、右焦点 为顶点的
三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设 为该双曲线上异于顶点的任一点,直线
和 与椭圆的交点分别为 、B和C、D.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线 、 的斜率分别为 、 ,证明 ;
(Ⅲ)是否存在常数 ,使得 恒成立?若存在,求 的值;若不存在,请说明理由.
参考答案
一、单选题
1、
【答案】
A
【分析】
根据椭圆方程求出 ,再根据椭圆的定义计算可得;
【详解】
解:椭圆 ,所以 ,即 ,设上焦点为 ,下焦点为 ,则
,因为 ,所以 ,即点 到下焦点的距离为 ;
故选:A
2、
【答案】
A
【分析】
由题意可知,直线 的方向向量与平面 的法向量平行,由此即可求出结果.
【详解】
直线l的一个方向向量为 ,平面 的一个法向量为 ,且 ,
所以 ,
所以 .
故选:A.
3、
【答案】
A
【分析】
将直线变形为 ,由 且 ,即可求出定点.
【详解】
将 变形为: ,令 且 ,解得
, ,
所以直线恒过定点 .
故选:A
4、
【答案】
D
【分析】
先求点 关于直线 对称的点 ,再根据两点之间线段最短,即可得解.
【详解】
如图,设 关于直线 对称的点为 ,
则有 ,可得 ,可得 ,
依题意可得“将军饮马”的最短总路程为 ,
此时 ,
故选:D.
5、
【答案】
D
【分析】
由圆的方程可确定圆心和半径,根据圆上点到定点距离最大值为 可求得结果.
【详解】
由 得: , 圆心 ,半径 ,
圆心到坐标原点的距离 ,
圆上的点到坐标原点的距离的最大值为 .
故选:D.
【点睛】
结论点睛:若圆心到圆外定点的距离为 ,半径为 ,则圆上的点到圆外定点距离的最大值为 ,最小值为
.
6、
【答案】
B
【分析】
解:通过题意分析可以得,连接 ,画图如下:
是 的中点,
,
,
,
.
因此正确答案为:B
7、
【答案】
C
【分析】
该金杯主体部分的上口外直径为 ,下底座外直径为 ,
且杯身最细之处到上杯口的距离是到下底座距离的2倍,
可设 代入双曲线方程可得
,
即 ,
作差可得 ,解得 ,
所以杯身最细处的周长为 .
因此正确答案为:C
8、
【答案】
C
【分析】
通过题意, ,双曲线 的焦点 到 的一条渐近线 的距离为 ,则 ,所
以 ,所以 ,所以 ,所以双曲线 的渐近线方程为 .
二、多选题
9、
【答案】
A;C
【分析】
对A,化简方程令 的系数为0求解即可.
对B,根据截距的定义辨析即可.
对C,求出直线的斜率再根据斜率与倾斜角的关系辨析即可.
对D,利用横纵坐标的差求解即可.
【详解】
对A,化简得直线 ,故定点为 .故A正确.
对B, 在 轴上的截距为 .故B错误.
对C,直线 的斜率为 ,故倾斜角 满足 , , ,
即 .故C正确.
对D, 因为直线 垂直于 轴,故 到 的距离为 .故D错误.
故选:AC.
10、
【答案】
A;B;D
【分析】
两圆方程作差后可得公共弦方程,从而可判断A的正误,求出圆 的圆心坐标后求出垂直平分线的方程后可判
断B的正误,利用垂径定理计算弦长后可判断C的正误,求出 到直线的距离后可求动点到直线距离的最大值,
从而可判断D的正误.
【详解】
对于选项A,因为圆 : , : ,
两式作差可得公共弦AB所在直线的方程为 ,即 ,故A正确;
对于选项B,圆 : 的圆心为 ,
则线段AB中垂线的斜率为 ,即线段AB中垂线方程为 ,
整理可得 ,故B正确;
对于选项C,圆心 到 的距离为 ,
又圆 的半径 ,所以 ,故C不正确;
对于选项D,P为圆 上一动点,圆心 到 的距离为 ,
又圆 的半径 ,所以P到直线AB距离的最大值为 ,故D正确.
故选:ABD.
11、
【答案】
A;B;D
【分析】
先变形得到 ,对四个选项一一分析,得到答案.
【详解】
变形得到 ,
A选项,双曲线交点在 轴上,故 ,
此时 应该经过第一,二,四象限,A不可能;
B选项,椭圆焦点在 轴上,故 ,
此时 经过第一,二,三象限,B不可能;
C选项,双曲线交点在 轴上,故 ,
此时 应该经过第一,三,四象限,C可能;
D选项,椭圆焦点在 轴上,故 ,
此时 经过第一,二,三象限,D不可能;
故选:ABD
12、
【答案】
C;D
【分析】
根据椭圆的几何性质可判断 为椭圆的短轴端点时,此时 最大,即可列不等式求解.
【详解】
由椭圆的性质可得当点 为椭圆的短轴端点时,此时 最大,
若 不可能为钝角,当点 为椭圆的短轴断点时,则 ,
则 ,即 ,
又焦点在 轴上 ,解得 ,
所以实数 的值可以是4,5,
故选:CD
三、填空题
13、
【答案】
(2)
【分析】
由椭圆的离心率大小即可求解椭圆的扁平程度.
【详解】
设椭圆方程的长半轴长与短半轴长分别为 , ,
则椭圆的离心率 ,
显然 越大, 越小,
由于三个椭圆的 分别为 ,且
又 则 ,
故椭圆盘(2)的离心率最小,故椭圆盘(2)最圆.
故答案为:(2)
14、
【答案】
【分析】
由椭圆方程求出焦点坐标,得出 的值,再由双曲线的离心率得出 ,进而可得双曲线的标准方程.
【详解】
由椭圆方程 ,可得焦点为
设双曲线的半焦距为 ,则 ,因双曲线的离心率为 ,则
故 ,所以 ,
所以双曲线的标准方程为:
故答案为:
15、
【答案】
【分析】
设 ,结合中点公式和“点差法”求得直线 的斜率,结合直线的点斜式方程,即可求解.
【详解】
设 ,
因为点 , 是 的中点,可得 ,
由 ,两式相减得 ,
即 ,所以直线 的方程为 ,即 .
故答案为: .
16、
【答案】
【分析】
根据已知直线的斜率,求出渐近线的斜率范围,推出 , 的关系,然后求出离心率的范围.
【详解】
由题意可得双曲线的渐近线方程为 ,
过双曲线上焦点 且平行于渐近线 的方程为 ,此直线与只与双曲线的上支有一个交点,要使
斜率为 的直线 经过双曲线的上焦点 的直线 与与双曲线的上、下两支相交,则 ,所以
,因此 ,
故答案为:
四、解答题
17、
【答案】
(1) ;(2) .
【分析】
(1) 中点为 , ,
直线 方程为: ,即 ;
(2) , ,
直线 方程为: ,即 .
18、
【答案】
(1)证明见解析;
(2) ;
(3)2.
【分析】
(1)在正方体 中, ,则四边形 为平行
四边形,
因此 ,而 平面 , 平面 ,
所以 平面 .
(2)在棱长为2的正方体 中,射线 两两垂直,以点A为原点建立如下图所
示的空间直角坐标系,
,棱 的中点 ,
,
设平面 的法向量 ,则 ,令 ,得
,
直线 与平面 所成的角为 ,则 ,
所以直线 与平面 所成角的正弦值为 .
(3)由(2)知, ,
所以点C到平面 的距离 .
19、
【答案】
(1) ,
(2) 或
【分析】
(1)根据题意,可分直线 的斜率不存在和存在两种情况讨论,结合直线与圆相切,利用点到直线的距离公
式,列出方程,即可求解;
(2)设 ,由两圆相外切,得到 ,列出方程求得 的值,即可求解.
【详解】
(1)解:由圆 ,可得原心 ,半径为 ,
当直线 的斜率不存在时,直线方程为 ,此时直线与圆相切,符合题意;
当直线 的斜率存在时,设直线 的方程为 ,即 ,
由圆心 到直线 的距离等于半径,可得 ,解得 ,
此时直线 的方程为 ,
综上可得,所求直线的方程为 或 .
(2)解:由圆 的半径为3,圆心在直线 上,
设 ,且圆 的圆心 ,半径为 ,
由两圆相外切,可得 ,即 ,
解得 或 ,所以 或 ,
所以所求圆的方程为 或 .
20、
【答案】
(1)2;
(2) ﹒
【分析】
(1)根据已知条件得 , ,结合离心率 ,即可解得答案.
(2)设直线的方程,与椭圆方程联立,利用弦长公式以及三角形的面积公式,基本不等式即可得出答案.
【详解】
(1)由题意可得, , ,
∵离心率 ,
∴ ,
∵ ,
∴ ,解得 .
(2)由(1)知,椭圆 ,上焦点 ,
设 , , , ,直线 的方程为: ,
联立 ,得 ,
∴ , ,
∴ ,
∴ ,
∴
,
当且仅当 ,即 时等号成立,
∴ 为原点)面积的最大值为 .
21、
【答案】
(1)
(2)不存在,理由见解析
【分析】
(1)建立空间直角坐标系,利用法向量的夹角求解即可,
(2)利用线面垂直的向量关系即可求解.
【详解】
(1)证明:取 中点 ,连接 .因为 ,所以 .
因为平面 平面 ,平面 平面 , 平面 ,
所以 平面 .取 中点 ,连接 ,则 .
以 为原点,如图建立空间直角坐标系,设 ,
则 , , , , , , .
平面 的法向量 ,设平面 的法向量 ,
由 ,得
令 ,则 .
所以 ,
所以平面 与平面 夹角的余弦值 ;
(2)在线段 上是不存在点 ,使得 平面 .
设点 ,且 , ,则 ,
所以 .
则 所以 , .
若 平面 ,则 ,即 ,此方程无解,
所以在线段 上不存在点 ,使得 平面 .
22、
【答案】
(Ⅰ)椭圆的标准方程为 ;双曲线的标准方程为
(Ⅱ) =1.(Ⅲ)存在常数 使得 恒成立,
【分析】
试题分析:(1)设椭圆的半焦距为c,通过题意知: ,
2a+2c=4( +1),所以a=2 ,c=2.
又a2=b2+c2,因此b=2.故椭圆的标准方程为 =1.
通过题意设等轴双曲线的标准方程为 =1(m>0),因为等轴双曲线的顶点是椭圆的焦点,所以m=2,
因此双曲线的标准方程为 =1.
(2)设A(x1,y1),B(x2,y2),P(x0,y0),则k1= ,k2= .
因为点P在双曲线x2-y2=4上,所以x-y=4.
因此k1·k2= · = =1,即k1·k2=1.
(3)由于PF1的方程为y=k1(x+2),将其代入椭圆方程得(2k +1)x
2-8k x+8k -8=0,
显然2k +1≠0,显然Δ>0.由韦达定理得x1+x2= ,x1x2= .
所以|AB|=
= .
同理可知|CD|= .
则 ,
又k1·k2=1,
所以 .
故|AB|+|CD|= |AB|·|CD|.
因此存在λ= ,使|AB|+|CD|=λ|AB|·|CD|恒成立.
考点:本题考查了圆锥曲线方程的求法及直线与圆锥曲线的位置关系
点评:对于直线与圆锥曲线的综合问题,往往要联立方程,同时结合一元二次方程根与系数的关系进行求解;
而对于最值问题,则可将该表达式用直线斜率k表示,然后通过题意将其进行化简结合表达式的形式选取最值的
计算方式
