2023-2024学年高中数学人教A版必修第二册第八章立体几何初步练习卷(含答案)
文档属性
| 名称 | 2023-2024学年高中数学人教A版必修第二册第八章立体几何初步练习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 749.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 14:53:02 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年高中数学人教A版必修第二册第八章立体几何初步练习卷
一、选择题
1.已知圆锥的底面半径为2,高为,则该圆锥的侧面积为( )
A. B. C. D.
2. 如图,在正方体中,E、F为正方体内(含边界)不重合的两个动点,下列结论错误的是( ).
A.若,,则
B.若,,则平面平面
C.若,,则面
D.若,,则
3.已知l,m,n是三条不同的直线,,,是三个不同的平面,给出下列命题,其中为假命题的是( )
A.若,,,则
B.若,,,,,则
C.若,,,,则
D.若m与n异面,,,则存在,使得,,
4.在正方体中,给出下列四个推断:
①
②
③平面平面
④平面平面
其中正确的推断有( )
A.1个 B.2个 C.3个 D.4个
5.中国古代数学经典九章算术系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑如图为一个阳马与一个鳖臑的组合体,已知平面,四边形为正方形,,,若鳖臑的外接球的体积为,则阳马的外接球的表面积等于( )
A. B. C. D.
6.埃及胡夫金字塔是世界古代建筑奇迹之一,它的形状可视为一个正四棱雉,其侧面与底面所成角的余弦值为,则侧面三角形的底角的正切值为( )
A.2 B.3 C. D.
7.分形几何学是一门以不规则几何形态为研究对象的几何学,分形几何具有自身相似性,从它的任何一个局部经过放 大,都可以得到一个和整体全等的图形. 如图的雪花曲线,将一个边长为 1 的正三角形的每条边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图 2,如此继续下去,得图(3)...不断重复这样的过程,便产生了雪花曲线。
记 为第个图形的面积, 如果这个作图过程可以一直继续下去, 则将趋近于多少( )
A. B. C. D.
8.如图,水平放置的正四棱台玻璃容器的高为,两底面对角线、的长分别为、,水深为则玻璃容器里面水的体积是 ( )
A. B. C. D.
二、多项选择题
9. 下列物体,能够被半径为的球体完全容纳的有( )
A.所有棱长均为的四面体
B.底面棱长为,高为正六棱锥
C.底面直径为,高为的圆柱
D.上 下底面的边长分别为,高为的正四棱台
10.在正三棱柱中,,则下列说法正确的是( )
A.正三棱柱的体积为
B.三棱锥的体积为
C.二面角的大小为
D.点到平面的距离为
11.如图,在直三棱柱中,,,则( )
A.平面
B.平面平面
C.异面直线AC与A,B所成的角的余弦值为
D.点,A,B,C均在半径为的球面上
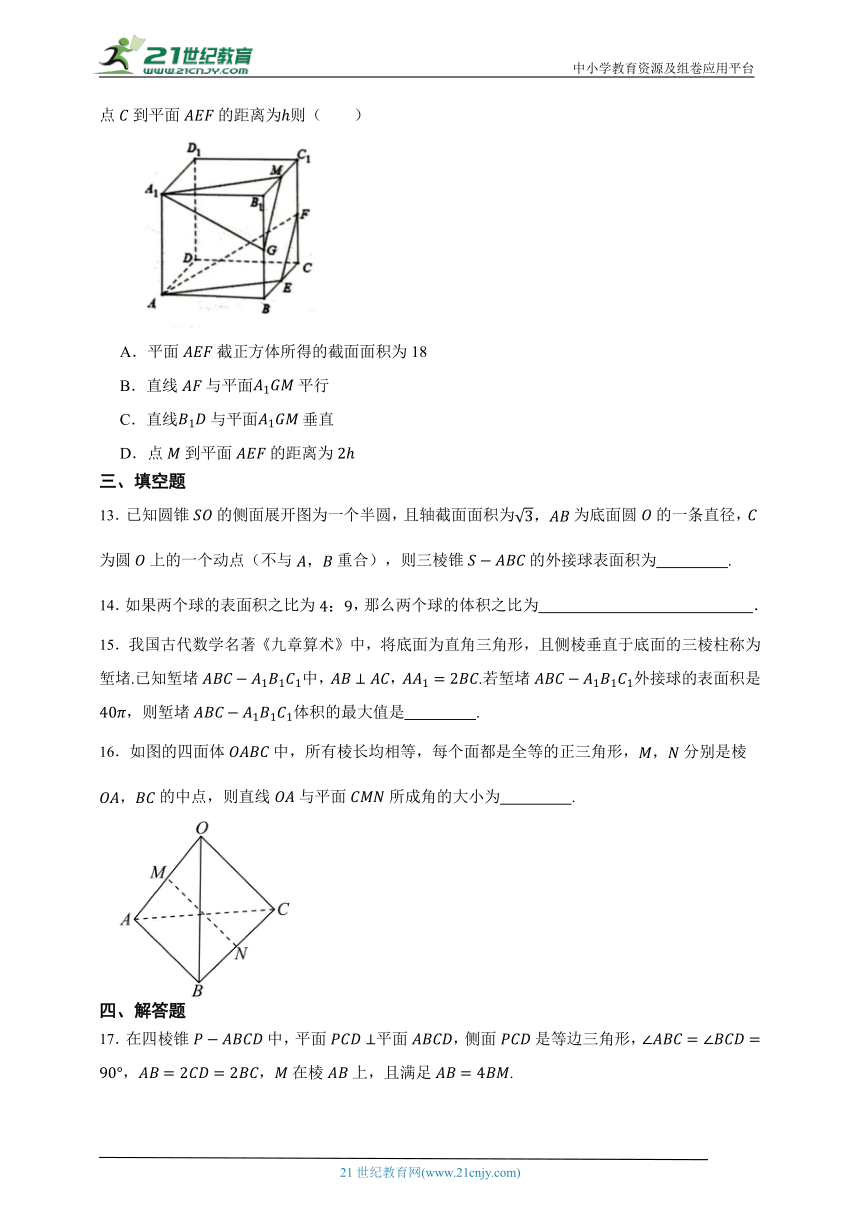
12.正方体的棱长为4,分别为的中点,点到平面的距离为则( )
A.平面截正方体所得的截面面积为18
B.直线与平面平行
C.直线与平面垂直
D.点到平面的距离为
三、填空题
13.已知圆锥的侧面展开图为一个半圆,且轴截面面积为为底面圆的一条直径,为圆上的一个动点(不与重合),则三棱锥的外接球表面积为 .
14.如果两个球的表面积之比为,那么两个球的体积之比为 .
15.我国古代数学名著《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵.已知堑堵中,,.若堑堵外接球的表面积是,则堑堵体积的最大值是 .
16.如图的四面体中,所有棱长均相等,每个面都是全等的正三角形,分别是棱的中点,则直线与平面所成角的大小为 .
四、解答题
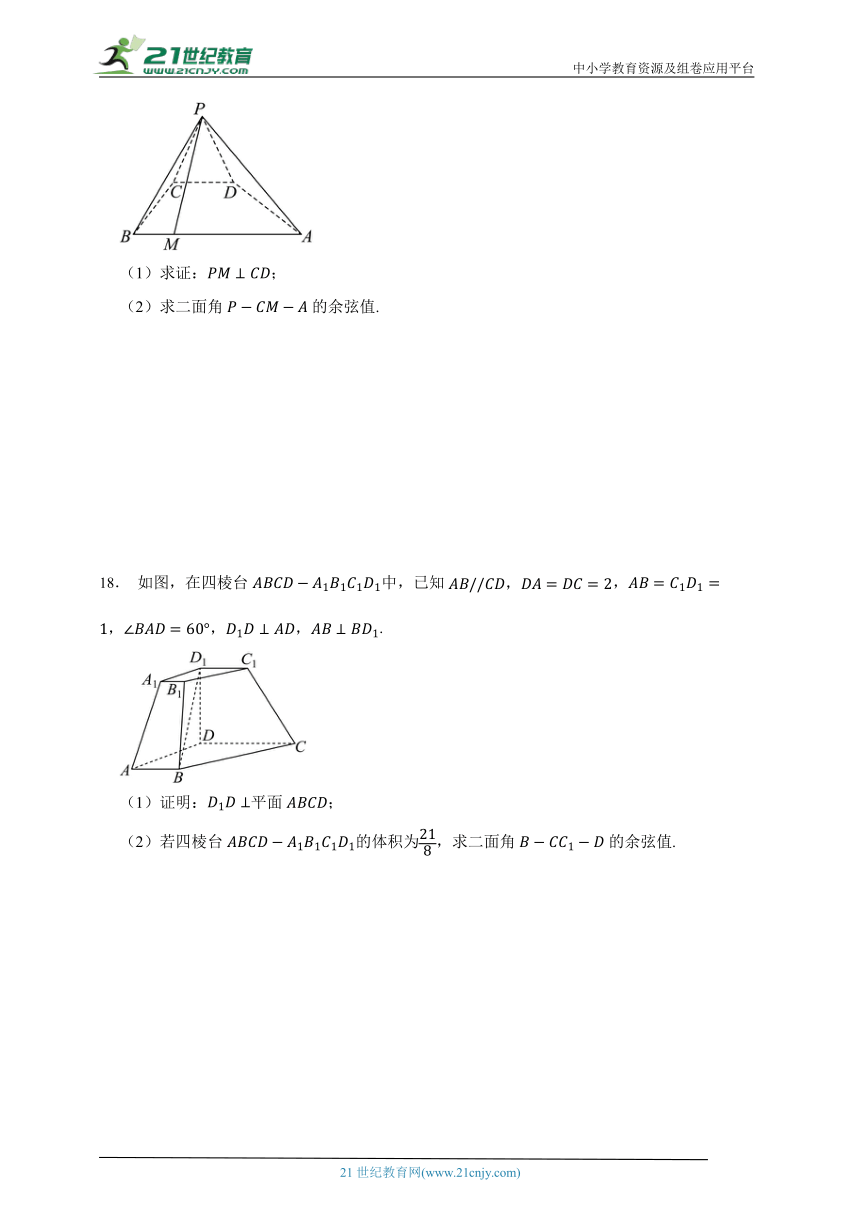
17.在四棱锥中,平面平面,侧面是等边三角形,,,在棱上,且满足.
(1)求证:;
(2)求二面角的余弦值.
18. 如图,在四棱台中,已知,.
(1)证明:平面;
(2)若四棱台的体积为,求二面角的余弦值.
19.三棱柱中,别为中点,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
20.如图,在四棱锥中,底面ABCD是边长为2的正方形,底面ABCD,,点E在棱PC上,平面EBD.
(1)试确定点E的位置,并说明理由;
(2)是否存在实数,使三棱锥体积为.
21.如图,四棱锥的底面为正方形,底面,、分别是、的中点.
(1)求证:平面;
(2)求证:平面平面.
22.如图,在四棱锥中,,四边形是菱形,是棱上的动点,且.
(1)证明:平面.
(2)是否存在实数,使得平面与平面所成锐二面角的余弦值是 若存在,求出的值;若不存在,请说明理由.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】A
9.【答案】A,B,D
10.【答案】A,C
11.【答案】A,B,C
12.【答案】A,B,D
13.【答案】
14.【答案】8:27(填也可以)
15.【答案】
16.【答案】
17.【答案】(1)证明略
(2)解:
18.【答案】(1)解:在四边形中,,
,
又平面
又平面;
(2)解:,
,
如图建系,
,
,设平面的一个法向量
平面的一个法向量,设二面角的平面角为,
显然为锐角,.
19.【答案】(1)解:连接,由于四边形是菱形,,
所以三角形是等边三角形,而是的中点,所以,
由于,平面,
所以平面,由于平面,所以,
由于四边形是菱形,,
所以三角形是等边三角形,所以.
由此以为空间坐标原点建立如图所示空间直角坐标系,
,
,
设平面的法向量为,
则,故可设,
所以,
由于平面,所以平面.
(2)解:,设直线与平面所成角为,
则.
20.【答案】(1)解:E是PC的中点.
证明:连结AC,交BD于点O,连结OE.
∵底面ABCD是正方形,
∴O是AC的中点.
∵平面EBD,平面平面,
∴.
∵O是AC的中点,
∴E是PC的中点.
(2)解:∵E为PC中点,
∴.
若,则.
∵.
∴.
∴存在,使三棱锥体积为.
21.【答案】(1)证明:如图,连接,则是的中点,
又是的中点,.
又平面,平面,
平面.
(2)证明:是正方形,,
平面,平面,,
又,平面,平面.
又平面,
故平面平面.
22.【答案】(1)证明:因为四边形是菱形,所以.
因为平面,且,所以平面.
因为平面,所以.
因为,所以,即.
因为平面,且,所以平面.
(2)解:取棱的中点,连接,易证两两垂直,
故以为原点,分别以的方向为轴的正方向,建立空间直角坐标系.
设,则,
故,
所以,
设平面的法向量为,则,
令,得.
平面的一个法向量为,设面与面所成的锐二面角为,
则,整理得,解得(舍去).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年高中数学人教A版必修第二册第八章立体几何初步练习卷
一、选择题
1.已知圆锥的底面半径为2,高为,则该圆锥的侧面积为( )
A. B. C. D.
2. 如图,在正方体中,E、F为正方体内(含边界)不重合的两个动点,下列结论错误的是( ).
A.若,,则
B.若,,则平面平面
C.若,,则面
D.若,,则
3.已知l,m,n是三条不同的直线,,,是三个不同的平面,给出下列命题,其中为假命题的是( )
A.若,,,则
B.若,,,,,则
C.若,,,,则
D.若m与n异面,,,则存在,使得,,
4.在正方体中,给出下列四个推断:
①
②
③平面平面
④平面平面
其中正确的推断有( )
A.1个 B.2个 C.3个 D.4个
5.中国古代数学经典九章算术系统地总结了战国、秦、汉时期的数学成就,书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑如图为一个阳马与一个鳖臑的组合体,已知平面,四边形为正方形,,,若鳖臑的外接球的体积为,则阳马的外接球的表面积等于( )
A. B. C. D.
6.埃及胡夫金字塔是世界古代建筑奇迹之一,它的形状可视为一个正四棱雉,其侧面与底面所成角的余弦值为,则侧面三角形的底角的正切值为( )
A.2 B.3 C. D.
7.分形几何学是一门以不规则几何形态为研究对象的几何学,分形几何具有自身相似性,从它的任何一个局部经过放 大,都可以得到一个和整体全等的图形. 如图的雪花曲线,将一个边长为 1 的正三角形的每条边三等分,以中间一段为边向形外作正三角形,并擦去中间一段,得图 2,如此继续下去,得图(3)...不断重复这样的过程,便产生了雪花曲线。
记 为第个图形的面积, 如果这个作图过程可以一直继续下去, 则将趋近于多少( )
A. B. C. D.
8.如图,水平放置的正四棱台玻璃容器的高为,两底面对角线、的长分别为、,水深为则玻璃容器里面水的体积是 ( )
A. B. C. D.
二、多项选择题
9. 下列物体,能够被半径为的球体完全容纳的有( )
A.所有棱长均为的四面体
B.底面棱长为,高为正六棱锥
C.底面直径为,高为的圆柱
D.上 下底面的边长分别为,高为的正四棱台
10.在正三棱柱中,,则下列说法正确的是( )
A.正三棱柱的体积为
B.三棱锥的体积为
C.二面角的大小为
D.点到平面的距离为
11.如图,在直三棱柱中,,,则( )
A.平面
B.平面平面
C.异面直线AC与A,B所成的角的余弦值为
D.点,A,B,C均在半径为的球面上
12.正方体的棱长为4,分别为的中点,点到平面的距离为则( )
A.平面截正方体所得的截面面积为18
B.直线与平面平行
C.直线与平面垂直
D.点到平面的距离为
三、填空题
13.已知圆锥的侧面展开图为一个半圆,且轴截面面积为为底面圆的一条直径,为圆上的一个动点(不与重合),则三棱锥的外接球表面积为 .
14.如果两个球的表面积之比为,那么两个球的体积之比为 .
15.我国古代数学名著《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵.已知堑堵中,,.若堑堵外接球的表面积是,则堑堵体积的最大值是 .
16.如图的四面体中,所有棱长均相等,每个面都是全等的正三角形,分别是棱的中点,则直线与平面所成角的大小为 .
四、解答题
17.在四棱锥中,平面平面,侧面是等边三角形,,,在棱上,且满足.
(1)求证:;
(2)求二面角的余弦值.
18. 如图,在四棱台中,已知,.
(1)证明:平面;
(2)若四棱台的体积为,求二面角的余弦值.
19.三棱柱中,别为中点,且.
(1)求证:平面;
(2)求直线与平面所成角的正弦值.
20.如图,在四棱锥中,底面ABCD是边长为2的正方形,底面ABCD,,点E在棱PC上,平面EBD.
(1)试确定点E的位置,并说明理由;
(2)是否存在实数,使三棱锥体积为.
21.如图,四棱锥的底面为正方形,底面,、分别是、的中点.
(1)求证:平面;
(2)求证:平面平面.
22.如图,在四棱锥中,,四边形是菱形,是棱上的动点,且.
(1)证明:平面.
(2)是否存在实数,使得平面与平面所成锐二面角的余弦值是 若存在,求出的值;若不存在,请说明理由.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】A
9.【答案】A,B,D
10.【答案】A,C
11.【答案】A,B,C
12.【答案】A,B,D
13.【答案】
14.【答案】8:27(填也可以)
15.【答案】
16.【答案】
17.【答案】(1)证明略
(2)解:
18.【答案】(1)解:在四边形中,,
,
又平面
又平面;
(2)解:,
,
如图建系,
,
,设平面的一个法向量
平面的一个法向量,设二面角的平面角为,
显然为锐角,.
19.【答案】(1)解:连接,由于四边形是菱形,,
所以三角形是等边三角形,而是的中点,所以,
由于,平面,
所以平面,由于平面,所以,
由于四边形是菱形,,
所以三角形是等边三角形,所以.
由此以为空间坐标原点建立如图所示空间直角坐标系,
,
,
设平面的法向量为,
则,故可设,
所以,
由于平面,所以平面.
(2)解:,设直线与平面所成角为,
则.
20.【答案】(1)解:E是PC的中点.
证明:连结AC,交BD于点O,连结OE.
∵底面ABCD是正方形,
∴O是AC的中点.
∵平面EBD,平面平面,
∴.
∵O是AC的中点,
∴E是PC的中点.
(2)解:∵E为PC中点,
∴.
若,则.
∵.
∴.
∴存在,使三棱锥体积为.
21.【答案】(1)证明:如图,连接,则是的中点,
又是的中点,.
又平面,平面,
平面.
(2)证明:是正方形,,
平面,平面,,
又,平面,平面.
又平面,
故平面平面.
22.【答案】(1)证明:因为四边形是菱形,所以.
因为平面,且,所以平面.
因为平面,所以.
因为,所以,即.
因为平面,且,所以平面.
(2)解:取棱的中点,连接,易证两两垂直,
故以为原点,分别以的方向为轴的正方向,建立空间直角坐标系.
设,则,
故,
所以,
设平面的法向量为,则,
令,得.
平面的一个法向量为,设面与面所成的锐二面角为,
则,整理得,解得(舍去).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
