寒假预习专项:圆柱与圆锥图形计算(含答案)数学六年级下册北师大版
文档属性
| 名称 | 寒假预习专项:圆柱与圆锥图形计算(含答案)数学六年级下册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 518.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 15:00:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
寒假预习专项:圆柱与圆锥图形计算-数学六年级下册北师大版
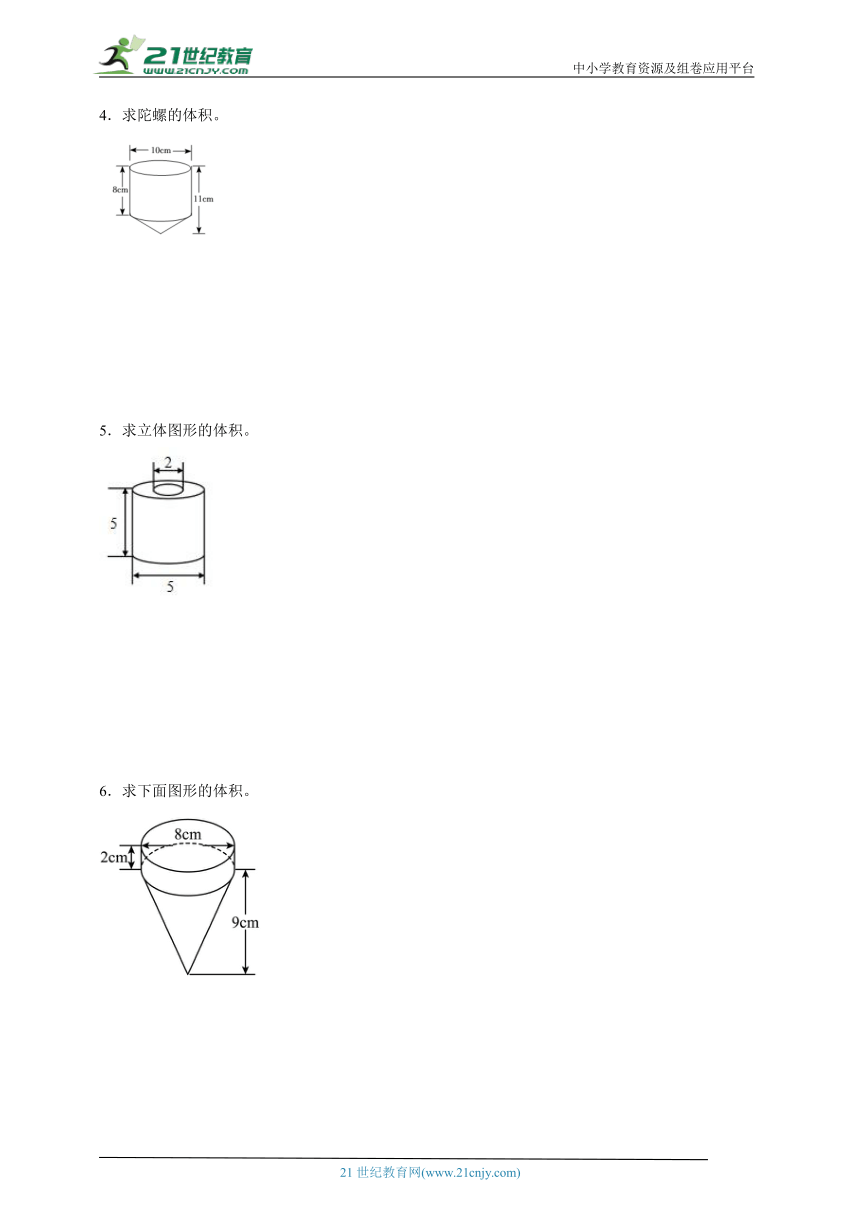
1.求圆柱的表面积和圆锥的体积。(单位:分米)
2.计算下面圆锥体的体积。
3.如图,把一根圆木锯成一半(单位:厘米),求这个半圆柱木料的体积。
4.求陀螺的体积。
5.求立体图形的体积。
6.求下面图形的体积。
7.求下面图形的表面积。
8.计算下面组合图形的体积。
9.计算下图的体积。
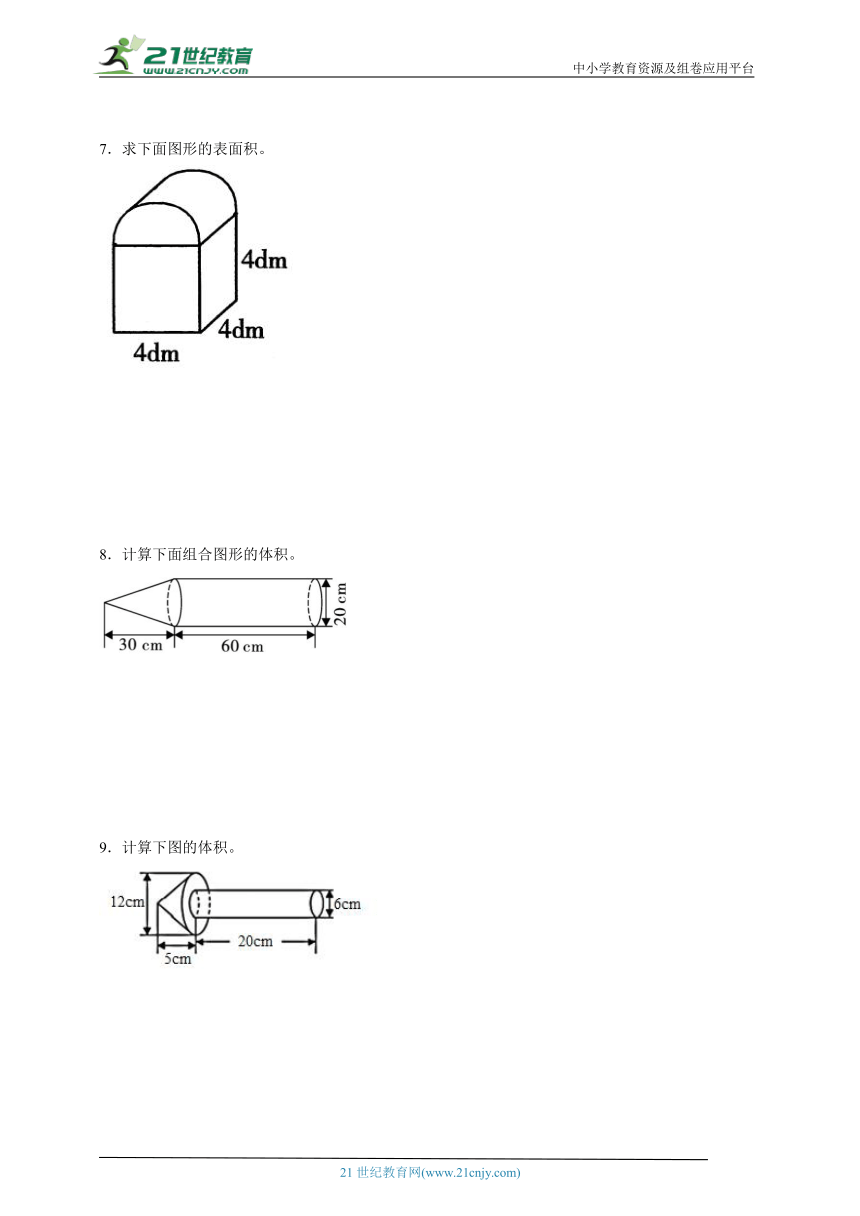
10.计算下面组合图形的体积。(单位:dm)
11.计算下面图形的体积。(单位:cm)
12.求如图中立体图形的体积。(单位:分米)
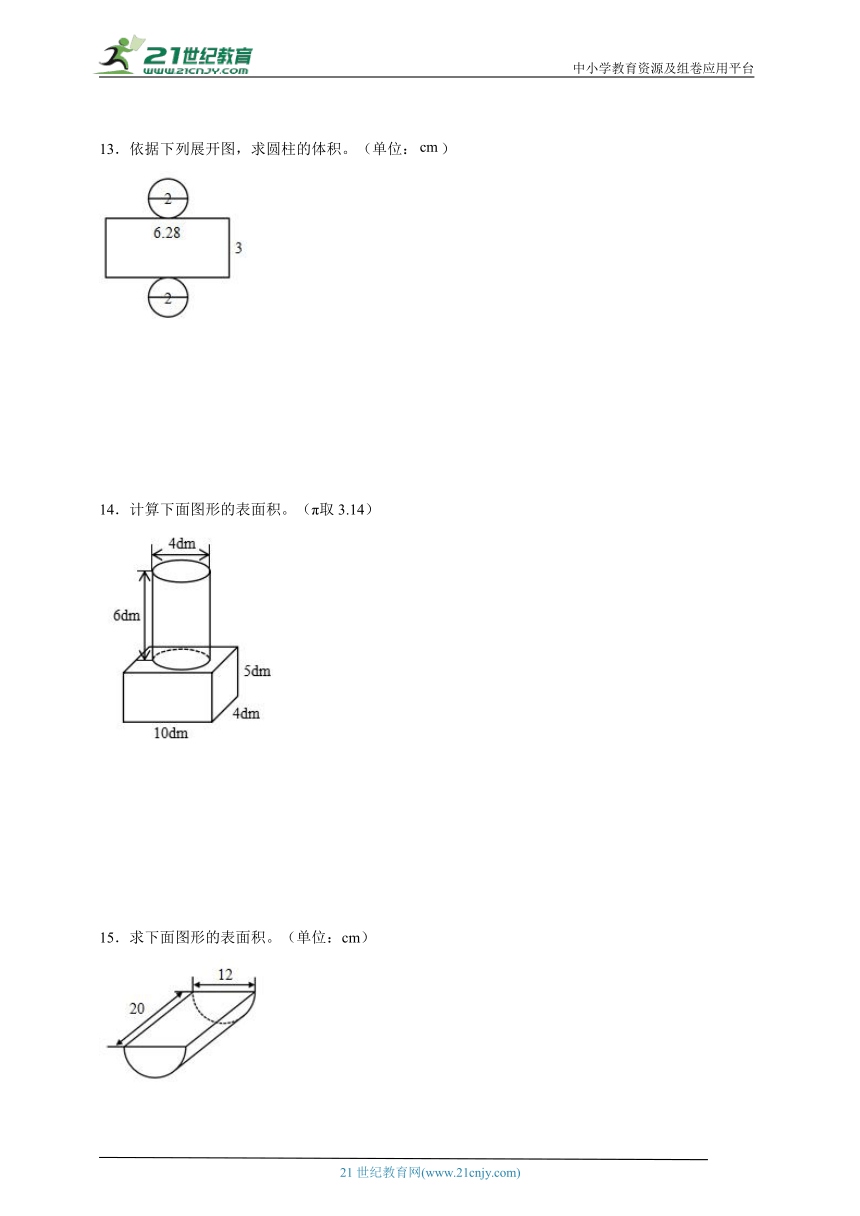
13.依据下列展开图,求圆柱的体积。(单位:)
14.计算下面图形的表面积。(π取3.14)
15.求下面图形的表面积。(单位:cm)
16.求下图组合体的体积。(单位:dm)
17.如图,将一个直角梯形以虚线为轴旋转一周后形成一个立体图形,求这个立体图形的体积。
18.求下面冰激凌的体积。(单位:cm)
参考答案:
1.158.256平方分米;100.48立方分米
【分析】根据圆柱的表面积公式:S=,圆锥的体积公式:V=,分别把数据代入到公式中,即可求出圆柱的表面积和圆锥的体积。
【详解】2×3.14×3×5.4+2×3.14×32
=6.28×3×5.4+6.28×9
=101.736+56.52
=158.256(平方分米)
=
=
=100.48(立方分米)
即圆柱的表面积是158.256平方分米,圆锥的体积是100.48立方分米。
2.75.36dm3
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】3.14×32×8
=3.14×9×8
=×9×3.14×8
=3×3.14×8
=75.36(dm3)
3.1130.4立方厘米
【分析】根据“”求出整个圆柱的体积,最后结果除以2求出半个圆柱木料的体积,据此解答。
【详解】3.14×(12÷2)2×20÷2
=3.14×62×20÷2
=113.04×20÷2
=2260.8÷2
=1130.4(立方厘米)
所以,这个半圆柱木料的体积是1130.4立方厘米。
4.706.5立方厘米
【分析】由题意可知:这个陀螺的体积等于直径为10厘米、高8厘米的圆柱的体积加上直径为10厘米、高(11-8)厘米的圆锥的体积,将数据代入圆柱、圆锥的体积公式计算即可。
【详解】3.14×(10÷2)2×8+×3.14×(10÷2)2×(11-8)
=3.14×52×8+×3.14×52×3
=3.14×25×8+×3×3.14×25
=628+78.5
=706.5(立方厘米)
5.82.425
【分析】这个立体图形的体积=底面直径是5,高是5的圆柱的体积-底面直径是2,高是5的圆柱的体积,根据圆柱的体积公式:底面积×高,代入数据,即可解答。
【详解】3.14×(5÷2)2×5-3.14×(2÷2)2×5
=3.14×6.25×5-3.14×1×5
=19.625×5-3.14×5
=98.125-15.7
=82.425
6.251.2立方厘米
【分析】上面是一个圆柱,圆柱的底面半径为(8÷2)厘米,高为2厘米,利用圆柱的体积公式:V=,代入求出上面圆柱的体积;下面是一个圆锥,圆锥的底面半径为(8÷2)厘米,高为9厘米,利用圆锥的体积公式:V=,代入求出上面圆锥的体积,把圆柱和圆锥的体积加起来,即可得解。
【详解】3.14×(8÷2)2×2+×3.14×(8÷2)2×9
=3.14×42×2+×9×3.14×42
=3.14×16×2+3×3.14×16
=100.48+150.72
=251.2(立方厘米)
7.117.68dm2
【分析】观察图形可知,该图形的表面积=正方体五个面的面积+圆柱的侧面积的一半+一个圆柱的底面积,根据正方体的表面积公式:S=6a2,圆柱的表面积公式:S=2πr2+πdh,据此解答即可。
【详解】4×4×5+3.14×4×4÷2+3.14×(4÷2)2
=16×5+25.12+12.56
=80+25.12+12.56
=105.12+12.56
=117.68(dm2)
8.21980cm3
【分析】组合图形的体积=底面直径是20cm,高是60cm的圆柱的体积+底面直径是20cm,高是30cm的圆锥的体积;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,代入数据,即可解答。
【详解】3.14×(20÷2)2×60+3.14×(20÷2)2×30×
=3.14×100×60+3.14×100×30×
=314×60+314×30×
=18840+9420×
=18840+3140
=21980(cm3)
9.753.6cm3
【分析】组合体的体积=底面直径6cm,高是20cm的圆柱的体积+底面直径12cm,高是5cm的圆锥的体积;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×;代入数据,即可解答。
【详解】3.14×(6÷2)2×20+3.14×(12÷2)2×5×
=3.14×9×20+3.14×36×5×
=28.26×20+113.04×5×
=565.2+565.2×
=565.2+188.4
=753.6(cm3)
10.110.56dm3
【分析】这个图形的体积等于圆锥和长方体的体积之和。长方体的体积=长×宽×高,圆锥的体积=底面积×高×=πr2h,据此代入数据求出两部分的体积,再把它们加起来即可。
【详解】
=110.56(dm3)
11.188.4cm3
【分析】用圆柱的体积减去空圆锥的体积即是所求图形的体积。圆柱的体积V=πr2h,圆锥的体积V=πr2h,据此代入数据计算。
【详解】3.14×(6÷2)2×8-×3.14×(6÷2)2×4
=3.14×72-3.14×12
=3.14×60
=188.4(cm3)
12.398.78立方分米
【分析】根据圆柱的体积=底面积×高,分别计算出两个圆柱的体积,再相加即可。
【详解】10÷2=5(分米)
6÷2=3(分米)
3.14×52×4
=3.14×25×4
=3.14×100
=314(立方分米)
3.14×32×3
=3.14×9×3
=28.26×3
=84.78(立方分米)
314+84.78=398.78(立方分米)
13.9.42cm3
【分析】因为3.14×2=6.28(cm),说明这个圆柱的底面直径是2cm,底面周长是6.28cm,可知高是3cm,先求出半径=2÷2=1(cm),再利用圆柱的体积公式:V=,代入求解即可。
【详解】2÷2=1(cm)
3.14×1×1×3
=3.14×3
=9.42(cm3)
所以这个圆柱的体积是9.42cm3。
14.295.36dm2
【分析】观察图形可知,图形的表面积=长是10dm,宽是4dm,高是5dm的长方体表面积+底面直径是4dm,高是6dm圆柱的侧面积;根据长方体表面积公式:(长×宽+长×高+宽×高)×2;圆柱的侧面积公式:底面周长×高,代入数据,即可解答。
【详解】(10×4+10×5+4×5)×2+3.14×4×6
=(40+50+20)×2+12.56×6
=(90+20)×2+75.36
=110×2+75.36
=220+75.36
=295.36(dm2)
15.729.84cm2
【分析】观察图形可知,图形的表面积是直径为12cm,高为20cm圆柱的表面积的一半,再加上长是20cm,宽是12cm的长方形面积;根据圆柱的表面积公式:底面积×2+侧面积;长方形面积公式:长×宽;代入数据,即可解答。
【详解】[3.14×(12÷2)2×2+3.14×12×20]÷2+20×12
=[3.14×36×2+37.68×20]÷2+240
=[113.04×2+753.6]÷2+240
=[226.08+753.6]÷2+240
=979.68÷2+240
=489.84+240
=729.84(cm2)
16.43.96dm3
【分析】V圆锥=,V圆柱=,组合体的体积=圆柱的体积+圆锥的体积×2,据此解答。
【详解】×3.14×(2÷2)2×3×2+3.14×(2÷2)2×(18-2×3)
=×3.14×1×3×2+3.14×1×(18-6)
=×3.14×1×3×2+3.14×1×12
=(×3)×(3.14×2)+3.14×12
=6.28+3.14×12
=6.28+37.68
=43.96(dm3)
17.160.14cm3
【分析】将一个直角梯形以虚线为轴旋转一周后,上方是一个圆锥,下方是一个圆柱,立体图形的体积=圆柱的体积+圆锥的体积,据此解答。
【详解】3.14×32×4+×3.14×32×(9-4)
=3.14×32×4+×3.14×32×5
=3.14×9×4+×3.14×9×5
=3.14×9×4+3.14×5×(×9)
=3.14×9×4+3.14×5×3
=3.14×(9×4+5×3)
=3.14×(36+15)
=3.14×51
=160.14(cm3)
18.122.46cm
【分析】冰激凌由两个圆锥组合而成,两个圆锥的半径相等,圆锥的体积,据此解答即可。
【详解】半径:6÷2=3(cm)
3.14×3 ×4×+3.14×3 ×9×
=3.14×9×4×+3.14×9×9×
=37.68+84.78
=122.46(cm )
【点睛】本题主要考查圆锥的体积,根据圆锥的体积公式“”解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
寒假预习专项:圆柱与圆锥图形计算-数学六年级下册北师大版
1.求圆柱的表面积和圆锥的体积。(单位:分米)
2.计算下面圆锥体的体积。
3.如图,把一根圆木锯成一半(单位:厘米),求这个半圆柱木料的体积。
4.求陀螺的体积。
5.求立体图形的体积。
6.求下面图形的体积。
7.求下面图形的表面积。
8.计算下面组合图形的体积。
9.计算下图的体积。
10.计算下面组合图形的体积。(单位:dm)
11.计算下面图形的体积。(单位:cm)
12.求如图中立体图形的体积。(单位:分米)
13.依据下列展开图,求圆柱的体积。(单位:)
14.计算下面图形的表面积。(π取3.14)
15.求下面图形的表面积。(单位:cm)
16.求下图组合体的体积。(单位:dm)
17.如图,将一个直角梯形以虚线为轴旋转一周后形成一个立体图形,求这个立体图形的体积。
18.求下面冰激凌的体积。(单位:cm)
参考答案:
1.158.256平方分米;100.48立方分米
【分析】根据圆柱的表面积公式:S=,圆锥的体积公式:V=,分别把数据代入到公式中,即可求出圆柱的表面积和圆锥的体积。
【详解】2×3.14×3×5.4+2×3.14×32
=6.28×3×5.4+6.28×9
=101.736+56.52
=158.256(平方分米)
=
=
=100.48(立方分米)
即圆柱的表面积是158.256平方分米,圆锥的体积是100.48立方分米。
2.75.36dm3
【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】3.14×32×8
=3.14×9×8
=×9×3.14×8
=3×3.14×8
=75.36(dm3)
3.1130.4立方厘米
【分析】根据“”求出整个圆柱的体积,最后结果除以2求出半个圆柱木料的体积,据此解答。
【详解】3.14×(12÷2)2×20÷2
=3.14×62×20÷2
=113.04×20÷2
=2260.8÷2
=1130.4(立方厘米)
所以,这个半圆柱木料的体积是1130.4立方厘米。
4.706.5立方厘米
【分析】由题意可知:这个陀螺的体积等于直径为10厘米、高8厘米的圆柱的体积加上直径为10厘米、高(11-8)厘米的圆锥的体积,将数据代入圆柱、圆锥的体积公式计算即可。
【详解】3.14×(10÷2)2×8+×3.14×(10÷2)2×(11-8)
=3.14×52×8+×3.14×52×3
=3.14×25×8+×3×3.14×25
=628+78.5
=706.5(立方厘米)
5.82.425
【分析】这个立体图形的体积=底面直径是5,高是5的圆柱的体积-底面直径是2,高是5的圆柱的体积,根据圆柱的体积公式:底面积×高,代入数据,即可解答。
【详解】3.14×(5÷2)2×5-3.14×(2÷2)2×5
=3.14×6.25×5-3.14×1×5
=19.625×5-3.14×5
=98.125-15.7
=82.425
6.251.2立方厘米
【分析】上面是一个圆柱,圆柱的底面半径为(8÷2)厘米,高为2厘米,利用圆柱的体积公式:V=,代入求出上面圆柱的体积;下面是一个圆锥,圆锥的底面半径为(8÷2)厘米,高为9厘米,利用圆锥的体积公式:V=,代入求出上面圆锥的体积,把圆柱和圆锥的体积加起来,即可得解。
【详解】3.14×(8÷2)2×2+×3.14×(8÷2)2×9
=3.14×42×2+×9×3.14×42
=3.14×16×2+3×3.14×16
=100.48+150.72
=251.2(立方厘米)
7.117.68dm2
【分析】观察图形可知,该图形的表面积=正方体五个面的面积+圆柱的侧面积的一半+一个圆柱的底面积,根据正方体的表面积公式:S=6a2,圆柱的表面积公式:S=2πr2+πdh,据此解答即可。
【详解】4×4×5+3.14×4×4÷2+3.14×(4÷2)2
=16×5+25.12+12.56
=80+25.12+12.56
=105.12+12.56
=117.68(dm2)
8.21980cm3
【分析】组合图形的体积=底面直径是20cm,高是60cm的圆柱的体积+底面直径是20cm,高是30cm的圆锥的体积;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×,代入数据,即可解答。
【详解】3.14×(20÷2)2×60+3.14×(20÷2)2×30×
=3.14×100×60+3.14×100×30×
=314×60+314×30×
=18840+9420×
=18840+3140
=21980(cm3)
9.753.6cm3
【分析】组合体的体积=底面直径6cm,高是20cm的圆柱的体积+底面直径12cm,高是5cm的圆锥的体积;根据圆柱的体积公式:底面积×高;圆锥的体积公式:底面积×高×;代入数据,即可解答。
【详解】3.14×(6÷2)2×20+3.14×(12÷2)2×5×
=3.14×9×20+3.14×36×5×
=28.26×20+113.04×5×
=565.2+565.2×
=565.2+188.4
=753.6(cm3)
10.110.56dm3
【分析】这个图形的体积等于圆锥和长方体的体积之和。长方体的体积=长×宽×高,圆锥的体积=底面积×高×=πr2h,据此代入数据求出两部分的体积,再把它们加起来即可。
【详解】
=110.56(dm3)
11.188.4cm3
【分析】用圆柱的体积减去空圆锥的体积即是所求图形的体积。圆柱的体积V=πr2h,圆锥的体积V=πr2h,据此代入数据计算。
【详解】3.14×(6÷2)2×8-×3.14×(6÷2)2×4
=3.14×72-3.14×12
=3.14×60
=188.4(cm3)
12.398.78立方分米
【分析】根据圆柱的体积=底面积×高,分别计算出两个圆柱的体积,再相加即可。
【详解】10÷2=5(分米)
6÷2=3(分米)
3.14×52×4
=3.14×25×4
=3.14×100
=314(立方分米)
3.14×32×3
=3.14×9×3
=28.26×3
=84.78(立方分米)
314+84.78=398.78(立方分米)
13.9.42cm3
【分析】因为3.14×2=6.28(cm),说明这个圆柱的底面直径是2cm,底面周长是6.28cm,可知高是3cm,先求出半径=2÷2=1(cm),再利用圆柱的体积公式:V=,代入求解即可。
【详解】2÷2=1(cm)
3.14×1×1×3
=3.14×3
=9.42(cm3)
所以这个圆柱的体积是9.42cm3。
14.295.36dm2
【分析】观察图形可知,图形的表面积=长是10dm,宽是4dm,高是5dm的长方体表面积+底面直径是4dm,高是6dm圆柱的侧面积;根据长方体表面积公式:(长×宽+长×高+宽×高)×2;圆柱的侧面积公式:底面周长×高,代入数据,即可解答。
【详解】(10×4+10×5+4×5)×2+3.14×4×6
=(40+50+20)×2+12.56×6
=(90+20)×2+75.36
=110×2+75.36
=220+75.36
=295.36(dm2)
15.729.84cm2
【分析】观察图形可知,图形的表面积是直径为12cm,高为20cm圆柱的表面积的一半,再加上长是20cm,宽是12cm的长方形面积;根据圆柱的表面积公式:底面积×2+侧面积;长方形面积公式:长×宽;代入数据,即可解答。
【详解】[3.14×(12÷2)2×2+3.14×12×20]÷2+20×12
=[3.14×36×2+37.68×20]÷2+240
=[113.04×2+753.6]÷2+240
=[226.08+753.6]÷2+240
=979.68÷2+240
=489.84+240
=729.84(cm2)
16.43.96dm3
【分析】V圆锥=,V圆柱=,组合体的体积=圆柱的体积+圆锥的体积×2,据此解答。
【详解】×3.14×(2÷2)2×3×2+3.14×(2÷2)2×(18-2×3)
=×3.14×1×3×2+3.14×1×(18-6)
=×3.14×1×3×2+3.14×1×12
=(×3)×(3.14×2)+3.14×12
=6.28+3.14×12
=6.28+37.68
=43.96(dm3)
17.160.14cm3
【分析】将一个直角梯形以虚线为轴旋转一周后,上方是一个圆锥,下方是一个圆柱,立体图形的体积=圆柱的体积+圆锥的体积,据此解答。
【详解】3.14×32×4+×3.14×32×(9-4)
=3.14×32×4+×3.14×32×5
=3.14×9×4+×3.14×9×5
=3.14×9×4+3.14×5×(×9)
=3.14×9×4+3.14×5×3
=3.14×(9×4+5×3)
=3.14×(36+15)
=3.14×51
=160.14(cm3)
18.122.46cm
【分析】冰激凌由两个圆锥组合而成,两个圆锥的半径相等,圆锥的体积,据此解答即可。
【详解】半径:6÷2=3(cm)
3.14×3 ×4×+3.14×3 ×9×
=3.14×9×4×+3.14×9×9×
=37.68+84.78
=122.46(cm )
【点睛】本题主要考查圆锥的体积,根据圆锥的体积公式“”解答。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
