等差数列前n项和第一课时(浙江省湖州市)
文档属性
| 名称 | 等差数列前n项和第一课时(浙江省湖州市) |

|
|
| 格式 | rar | ||
| 文件大小 | 262.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-27 00:00:00 | ||
图片预览






文档简介
课件22张PPT。一.复习回顾:等差数列性质:(1) 等差数列8,5,2,…,的第20项是 ;
(2)等差数列-5,-9,-13,…的第n项是 ;
(3) 已知{an}为等差数列,若a1=3,d= ,an=21,
则n = ;
(4) 已知{an}为等差数列,若a10= ,d= ,则
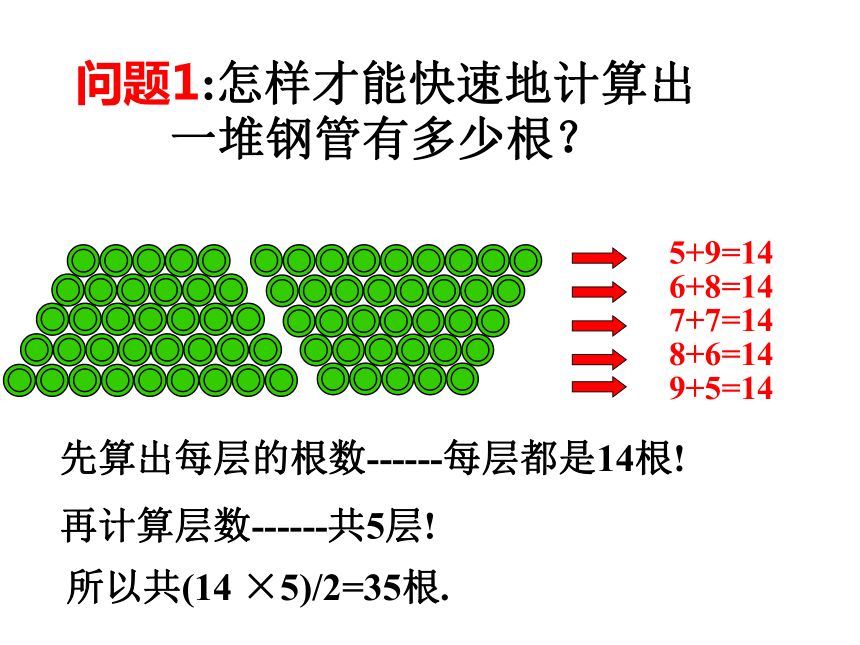
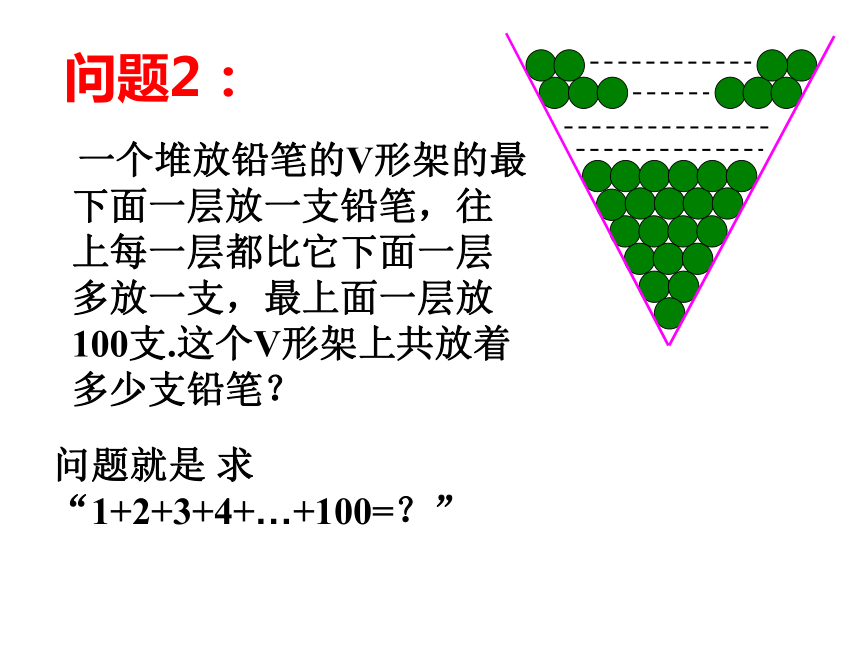
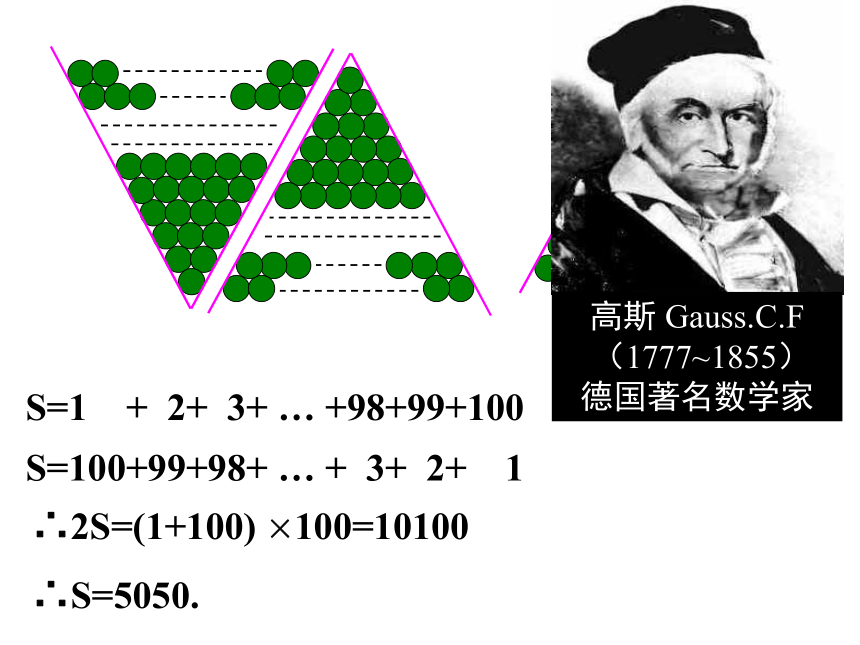
a3= .-4913(5)在数列{an}中a1=1,an= an+1+4,则a10= .-35复习巩固an = -5+(n-1).(-4)一、填空题:an=-4n-1CC 复习巩固二、选择题:等差数列的前n项和(一)学习目标:1、掌握等差数列前n项和公式及其推导过程;2、初步掌握公式的简单运用。教学重点、难点:重点是等差数列前n项和公式,难点是获得推导公式的思路。[克服难点的关键 是通过具体例子发现一般规律]问题1:怎样才能快速地计算出一堆钢管有多少根?5+9=146+8=147+7=148+6=149+5=14先算出每层的根数------每层都是14根!再计算层数------共5层!所以共(14 ×5)/2=35根.问题2: 一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支.这个V形架上共放着多少支铅笔?问题就是 求“1+2+3+4+…+100=?”S=1 + 2+ 3+ … +98+99+100 S=100+99+98+ … + 3+ 2+ 1 ∴2S=(1+100) ×100=10100
∴S=5050.问题3:求和:1+2+3+4+…+n=?记:S= 1 + 2 + 3 +…+(n-2)+(n-1)+nS= n+(n-1)+(n-2)+…+ 3 + 2 +1上述求解过程带给我们什么启示?(1)所求的和可以用首项、末项及项数来表示;
(2)等差数列中任意的第k项与倒数第k项的和都等于首项与末项的和。问题4:设等差数列 {an} 的首项为a1,公差为d,如何求等差数列的前n项和Sn= a1 +a2+a3+…+an?解:因为a1+an=a2+an-1=a3+an-2=… 两式左右分别相加,得倒序相加S=a1+ a2 +a3 +…+an-2+an-1+anS=an+an-1+an-2+…+a3 + a2 +a12Sn=(a1+an)+ (a2+an-1)+ (a3+an-2)+…+
(an-2+a3)+ (an-1+a2)+ (an+a1)=n(a1+an)变式:能否用
a1,n,d表示Sn?an=a1+(n-1)d公式与梯形面积:补成平形四边形分割成一个平行四边形和一个三角形 两个公式的共同已量是a1和n,不同的已知量是:公式(1)已知an,公式(2)已知d 。 已知三个量就可以求出Sn ,我们要根据具体题目,灵活采用这两个公式。 (n-1)d说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。
等差数列{an}的首项为a1,公差为d,项数为n,第n项为an,前n项和为Sn,请填写下表: 9550010022150.7604.5解:练习:
P42 2求和 (1) 1+3+5+ ··· +(2n-1) 例2 :(1)原式==n2解:
(2)-10,-6,-2, 2, ···, (4n-14)-10-6-2 + 2 + ··· +(4n-14)(2)原式=注意在运用公式时,
要看清等差数列的项数。 例3:等差数列-10,-6,-2,2,··· 前9项的和多少?
解:设题中的等差数列为{an}则 a1=-10,能用公式(1)计算吗? 应用公式时,要根据题目的具体条件,灵活选取这两个公式 。d=4,n=9 变式:等差数列-10,-6,-2,2,·······前多少项和是54 ? 解: 设题中的等差数列为{an}, 得 n2-6n-27=0
??????? 故 n1=9, n2=-3(舍去)。 在等差数列的求和公式中,含有四个量,运用方程的思想,知三可求一. d= -4 设 Sn= 54,则 a1= -10, 因此,等差数列 -10,-6,-2,2······· 前9项和是54。 1.推导等差数列前 n项和公式的方法
三.小结2.公式的应用中的数学思想.
-------倒序相加法
--------方程思想再见例6.在等差数列{an}中,
(1)已知d=3,an=20,Sn=65,
求a1和n以及此数列的后6项和;
(2) 已知an=11-3n,求Sn.
(3)已知a11=-1,求S21.备用:例7. 已知一个等差数列的前10项的和是310,前20项的和是1220,求其前n项和的公式.EX.1.若一个等差数列前3项和为34,最后三项和为146,且所有项的和为390,则这个数列共有______项。2.已知两个等差数列{an},{bn},它们的前n项和分别是Sn,Tn,若
(2)等差数列-5,-9,-13,…的第n项是 ;
(3) 已知{an}为等差数列,若a1=3,d= ,an=21,
则n = ;
(4) 已知{an}为等差数列,若a10= ,d= ,则
a3= .-4913(5)在数列{an}中a1=1,an= an+1+4,则a10= .-35复习巩固an = -5+(n-1).(-4)一、填空题:an=-4n-1CC 复习巩固二、选择题:等差数列的前n项和(一)学习目标:1、掌握等差数列前n项和公式及其推导过程;2、初步掌握公式的简单运用。教学重点、难点:重点是等差数列前n项和公式,难点是获得推导公式的思路。[克服难点的关键 是通过具体例子发现一般规律]问题1:怎样才能快速地计算出一堆钢管有多少根?5+9=146+8=147+7=148+6=149+5=14先算出每层的根数------每层都是14根!再计算层数------共5层!所以共(14 ×5)/2=35根.问题2: 一个堆放铅笔的V形架的最下面一层放一支铅笔,往上每一层都比它下面一层多放一支,最上面一层放100支.这个V形架上共放着多少支铅笔?问题就是 求“1+2+3+4+…+100=?”S=1 + 2+ 3+ … +98+99+100 S=100+99+98+ … + 3+ 2+ 1 ∴2S=(1+100) ×100=10100
∴S=5050.问题3:求和:1+2+3+4+…+n=?记:S= 1 + 2 + 3 +…+(n-2)+(n-1)+nS= n+(n-1)+(n-2)+…+ 3 + 2 +1上述求解过程带给我们什么启示?(1)所求的和可以用首项、末项及项数来表示;
(2)等差数列中任意的第k项与倒数第k项的和都等于首项与末项的和。问题4:设等差数列 {an} 的首项为a1,公差为d,如何求等差数列的前n项和Sn= a1 +a2+a3+…+an?解:因为a1+an=a2+an-1=a3+an-2=… 两式左右分别相加,得倒序相加S=a1+ a2 +a3 +…+an-2+an-1+anS=an+an-1+an-2+…+a3 + a2 +a12Sn=(a1+an)+ (a2+an-1)+ (a3+an-2)+…+
(an-2+a3)+ (an-1+a2)+ (an+a1)=n(a1+an)变式:能否用
a1,n,d表示Sn?an=a1+(n-1)d公式与梯形面积:补成平形四边形分割成一个平行四边形和一个三角形 两个公式的共同已量是a1和n,不同的已知量是:公式(1)已知an,公式(2)已知d 。 已知三个量就可以求出Sn ,我们要根据具体题目,灵活采用这两个公式。 (n-1)d说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。
等差数列{an}的首项为a1,公差为d,项数为n,第n项为an,前n项和为Sn,请填写下表: 9550010022150.7604.5解:练习:
P42 2求和 (1) 1+3+5+ ··· +(2n-1) 例2 :(1)原式==n2解:
(2)-10,-6,-2, 2, ···, (4n-14)-10-6-2 + 2 + ··· +(4n-14)(2)原式=注意在运用公式时,
要看清等差数列的项数。 例3:等差数列-10,-6,-2,2,··· 前9项的和多少?
解:设题中的等差数列为{an}则 a1=-10,能用公式(1)计算吗? 应用公式时,要根据题目的具体条件,灵活选取这两个公式 。d=4,n=9 变式:等差数列-10,-6,-2,2,·······前多少项和是54 ? 解: 设题中的等差数列为{an}, 得 n2-6n-27=0
??????? 故 n1=9, n2=-3(舍去)。 在等差数列的求和公式中,含有四个量,运用方程的思想,知三可求一. d= -4 设 Sn= 54,则 a1= -10, 因此,等差数列 -10,-6,-2,2······· 前9项和是54。 1.推导等差数列前 n项和公式的方法
三.小结2.公式的应用中的数学思想.
-------倒序相加法
--------方程思想再见例6.在等差数列{an}中,
(1)已知d=3,an=20,Sn=65,
求a1和n以及此数列的后6项和;
(2) 已知an=11-3n,求Sn.
(3)已知a11=-1,求S21.备用:例7. 已知一个等差数列的前10项的和是310,前20项的和是1220,求其前n项和的公式.EX.1.若一个等差数列前3项和为34,最后三项和为146,且所有项的和为390,则这个数列共有______项。2.已知两个等差数列{an},{bn},它们的前n项和分别是Sn,Tn,若
