等差数列前n项和第2课时
图片预览







文档简介
课件21张PPT。等差数列的前n项和(二)复习回顾1.等差数列前n项和Sn公式的推导
2.等差数列前n项和Sn公式:an=a1+(n-1)d说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。-------倒序相加法等差数列的性质:设数列{an}为等差数列,公差d仍成等差数列,其公差为k2d例1.已知等差数列{an}的前10项的和是 310,第11项到第20项的和是910,求第21项到第30项的和。解:设等差数列的首项为a1,公差为d,由题意,得例1.已知等差数列{an}的前10项的和是 310,第11项到第20项的和是910,求第21项到第30项的和。解:设等差数列的首项为a1,公差为d,由题意,得思考:P42变题1.已知等差数列{an}的前m项的和是
30,前2m项的和是100,求前3m项
的和。变题2.已知等差数列{an}中,S10=100,
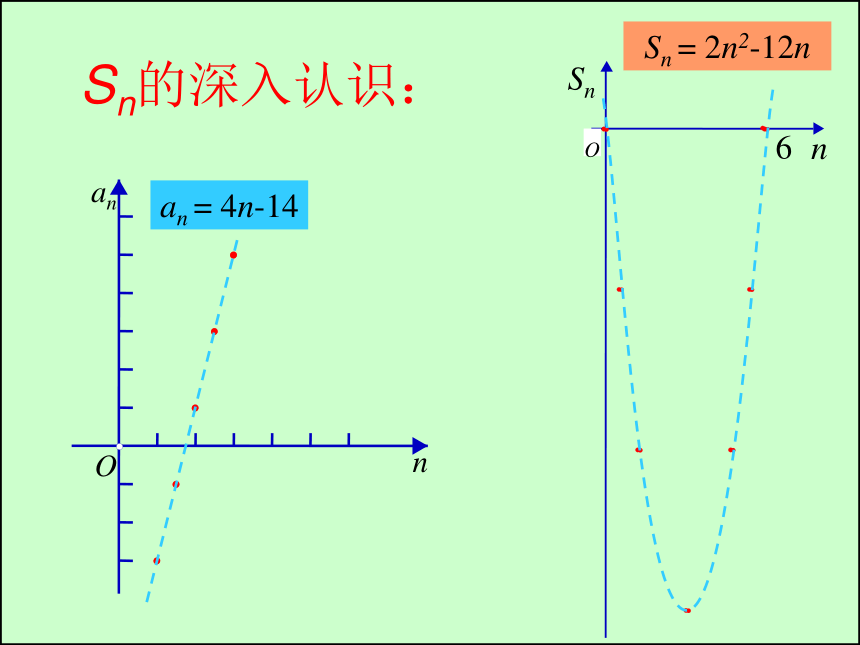
S100=10,求S110。练习 P42 3 4例2 .若数列{an}的前n项和sn=-2n2+n,{an}是否为等差数列?若是,给予证明,若不是,说明理由。变式.数列{an}的前n项和sn=-2n2+n+1,{an}是否为等差数列?若是,给予证明,若不是,说明理由。证明:所以数列{an}是等差数列反思:1.an=?;从函数的角度怎样理解?an = 4n-14Sn = 2n2-12n2. Sn呢?等差数列-10,-6,-2,2, …Sn的深入认识:an = 4n-14Sn = 2n2-12n反思公式思考:当首项、公差确定时,Sn的结构有什么特征?2.当d不为0时,点(n,Sn)是在常数项为0的一个二次函数的图象上。 结论1:{an}为等差数列? ,这是一个关于 的
没有 的“ ” Sn=an2+bn常数项二次函数( 注意 a 还可以是 0)n判断等差数列的方法:一.定义法:三.通项法:二.等差中项法:四.前n项和法:证明方法解法1:设所给数列为{an},则a1=16,d=-2.于是8 ..9例3:已知等差数列16,14,12,10, … 问:前多少项的和最大?并求出最大值。= -n2+17nSnn解法2:设所给数列为{an},则a1=16,d=-2.于是自我小结:一个等差数列的前n项和Sn,在什么时候 有最大值? 什么时候有最小值? 例3:已知等差数列16,14,12,10, … 问:前多少项的和最大?并求出最大值。ann设所给数列为{an},前n项和最大,则 练习2.等差数列{an}中,已知an=2(n-12),求此数列前n项和的最小值。归纳:(1)当a1>0,d>0时,Sn有最小值无最大值,
且最小值为S1;
(2)当a1>0,d<0时,Sn有最大值无最小值,
当am≥0且am+1≤0,Sn的最大值为Sm;
(3)当a1<0,d>0时,Sn有最小值无最大值,
当am≤0且am+1≥0,Sn的最小值为Sm;
(4)当a1<0,d<0时,Sn有最大值无最小值,
且最大值为S1。 练习1: 等差数列-10,-6,-2,2,…的前多少项的和最小?练3.已知等差数列{an}中,a1=-25,S3=S8,则前n项和Sn中,最小值为________练4.已知等差数列{an}中,a1<0,S9=S12,则该数列前多少项和最小?-7510或11变题1.设等差数列{an}满足3a8=5a13,且a1>0,
Sn为其前n项和,问:该数列前多少项
的和最小?变题2.等差数列{an}中,a1<0,Sn为其前n项
和,S9=S12,问:该数列前多少项的和
最小?变题3.等差数列{an}中,前n项和Sn的最大值
为S7,|a7|<|a8| ,求使Sn>0的n的最
大值。再见 例5.若一个等差数列前3项和为34,最后三项和为146,且所有项的和为390,则这个数列共有______项。
练习:1.求集合 的元素个数,并求这些元素的和.解:由 得∴正整数 共有14个即 中共有14个元素即:7,14,21,…,98 是以 为首项,以 为末项的等差数列.∴巩固练习1、已知 a6+a9+a12+a15=192,求 S202、凸 n 边形各内角成等差数列,公差为 10o,最小内角为 100o,则等于( )
(A)7 (B)8 (C)9 (D)8或 9由题意,得 :解得 n=8 或 9,但 n=9时,a9=180 o,不合题意,故选(B)B
2.等差数列前n项和Sn公式:an=a1+(n-1)d说明:两个等差数列的求和公式及通项公式,一共涉及到5个量,通常已知其中3个,可求另外2个。-------倒序相加法等差数列的性质:设数列{an}为等差数列,公差d仍成等差数列,其公差为k2d例1.已知等差数列{an}的前10项的和是 310,第11项到第20项的和是910,求第21项到第30项的和。解:设等差数列的首项为a1,公差为d,由题意,得例1.已知等差数列{an}的前10项的和是 310,第11项到第20项的和是910,求第21项到第30项的和。解:设等差数列的首项为a1,公差为d,由题意,得思考:P42变题1.已知等差数列{an}的前m项的和是
30,前2m项的和是100,求前3m项
的和。变题2.已知等差数列{an}中,S10=100,
S100=10,求S110。练习 P42 3 4例2 .若数列{an}的前n项和sn=-2n2+n,{an}是否为等差数列?若是,给予证明,若不是,说明理由。变式.数列{an}的前n项和sn=-2n2+n+1,{an}是否为等差数列?若是,给予证明,若不是,说明理由。证明:所以数列{an}是等差数列反思:1.an=?;从函数的角度怎样理解?an = 4n-14Sn = 2n2-12n2. Sn呢?等差数列-10,-6,-2,2, …Sn的深入认识:an = 4n-14Sn = 2n2-12n反思公式思考:当首项、公差确定时,Sn的结构有什么特征?2.当d不为0时,点(n,Sn)是在常数项为0的一个二次函数的图象上。 结论1:{an}为等差数列? ,这是一个关于 的
没有 的“ ” Sn=an2+bn常数项二次函数( 注意 a 还可以是 0)n判断等差数列的方法:一.定义法:三.通项法:二.等差中项法:四.前n项和法:证明方法解法1:设所给数列为{an},则a1=16,d=-2.于是8 ..9例3:已知等差数列16,14,12,10, … 问:前多少项的和最大?并求出最大值。= -n2+17nSnn解法2:设所给数列为{an},则a1=16,d=-2.于是自我小结:一个等差数列的前n项和Sn,在什么时候 有最大值? 什么时候有最小值? 例3:已知等差数列16,14,12,10, … 问:前多少项的和最大?并求出最大值。ann设所给数列为{an},前n项和最大,则 练习2.等差数列{an}中,已知an=2(n-12),求此数列前n项和的最小值。归纳:(1)当a1>0,d>0时,Sn有最小值无最大值,
且最小值为S1;
(2)当a1>0,d<0时,Sn有最大值无最小值,
当am≥0且am+1≤0,Sn的最大值为Sm;
(3)当a1<0,d>0时,Sn有最小值无最大值,
当am≤0且am+1≥0,Sn的最小值为Sm;
(4)当a1<0,d<0时,Sn有最大值无最小值,
且最大值为S1。 练习1: 等差数列-10,-6,-2,2,…的前多少项的和最小?练3.已知等差数列{an}中,a1=-25,S3=S8,则前n项和Sn中,最小值为________练4.已知等差数列{an}中,a1<0,S9=S12,则该数列前多少项和最小?-7510或11变题1.设等差数列{an}满足3a8=5a13,且a1>0,
Sn为其前n项和,问:该数列前多少项
的和最小?变题2.等差数列{an}中,a1<0,Sn为其前n项
和,S9=S12,问:该数列前多少项的和
最小?变题3.等差数列{an}中,前n项和Sn的最大值
为S7,|a7|<|a8| ,求使Sn>0的n的最
大值。再见 例5.若一个等差数列前3项和为34,最后三项和为146,且所有项的和为390,则这个数列共有______项。
练习:1.求集合 的元素个数,并求这些元素的和.解:由 得∴正整数 共有14个即 中共有14个元素即:7,14,21,…,98 是以 为首项,以 为末项的等差数列.∴巩固练习1、已知 a6+a9+a12+a15=192,求 S202、凸 n 边形各内角成等差数列,公差为 10o,最小内角为 100o,则等于( )
(A)7 (B)8 (C)9 (D)8或 9由题意,得 :解得 n=8 或 9,但 n=9时,a9=180 o,不合题意,故选(B)B
