抛物线的几何性质(1)
图片预览





文档简介
课件27张PPT。抛物线的几何性质
(一)制作者:赵娅辰高二年级 数学
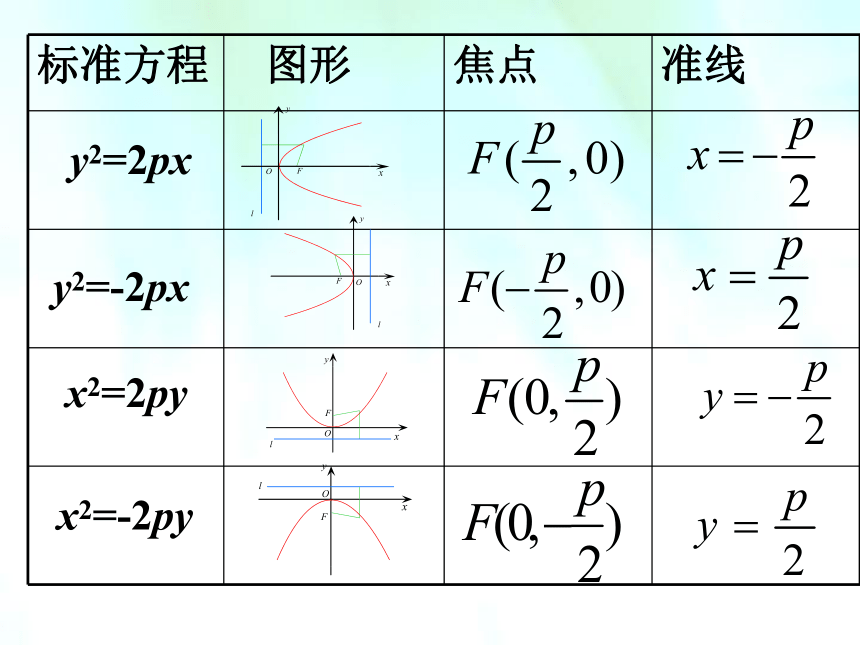
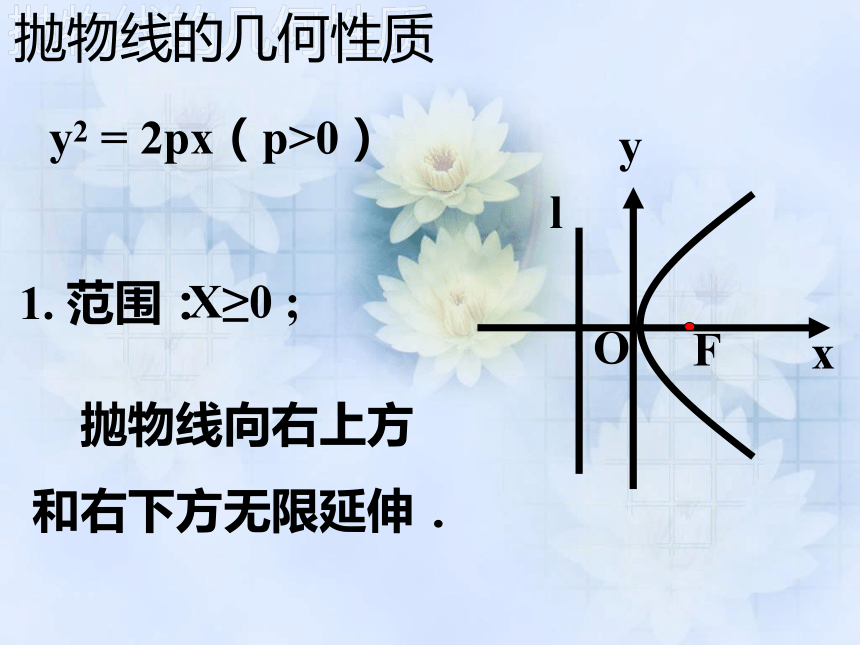
第二章 第三节生活中的抛物线y2=2pxy2=-2pxx2=2pyx2=-2pyy2 = 2px(p>0)1. 范围:X≥0 ; 抛物线向右上方
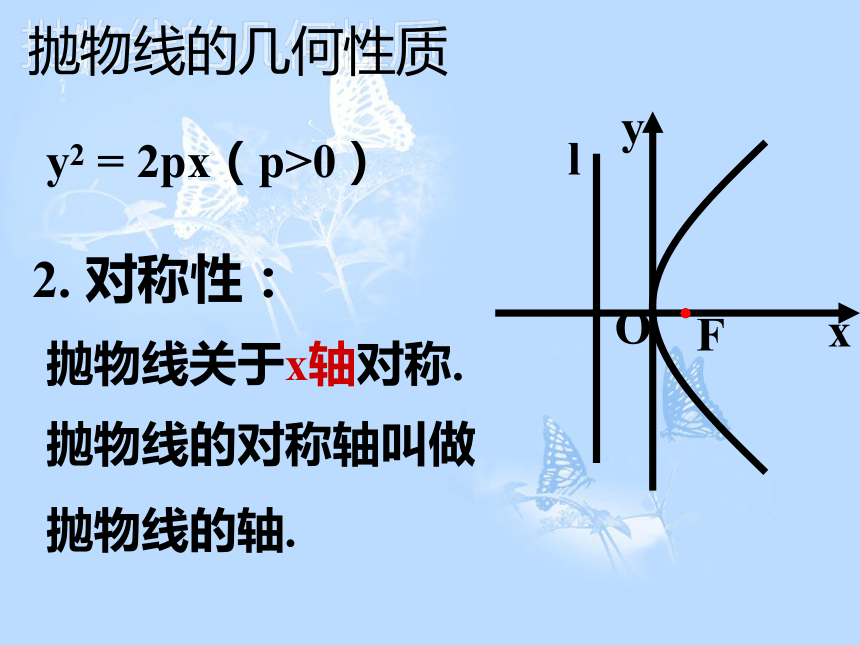
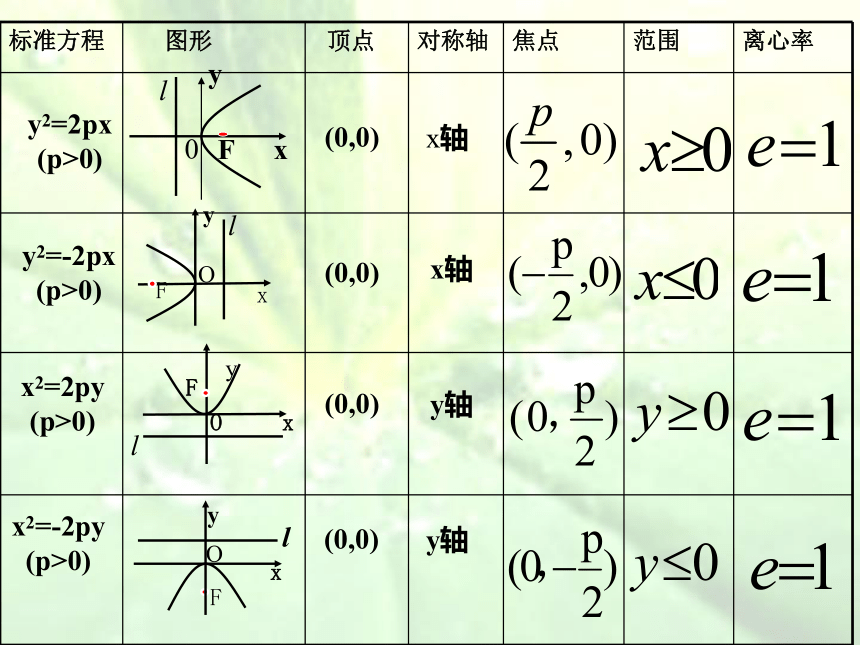
和右下方无限延伸. 抛物线的几何性质y2 = 2px(p>0)2. 对称性:抛物线关于x轴对称. 抛物线的几何性质抛物线的对称轴叫做抛物线的轴. y2 = 2px(p>0)抛物线和它的轴的交点叫做抛物线的顶点. 3. 顶点:4. 离心率:e =1 抛物线的几何性质y2=2px
(p>0)Oy2=-2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,0)(0,0)(0,0)(0,0)x轴x轴y轴y轴xyFlxyOFlDD3解:根据题意,可设它的标准方程为
y2 =2px ( p > 0 ).因为点M在抛物线上,所以即 p=2.因此所求方程为y2 =4x.思考(2)你有办法画出它的图像?将已知方程变形为y= 2 ,根据 y =2 , 计算抛物线在x 0的范围内几个点的坐标,得用光滑的曲线连结这些点;然后利用抛物线的对称性作出另一部分图像.过焦点且垂直于对称轴的直线被抛物线截得的线段AB叫做抛物线的通径.连结:过抛物线 的焦点F作垂直与轴的直线,交抛物线于A、B两点,则以AB 为直径的圆的方程是AB通径长为2p.CD拓展:xyOFABB’A’ 引伸: 过抛物线y2=2px的焦点F任作一条直线m,交这抛物线于A、B两点,求证:以AB为直径的圆和这抛物线的准线相切.OFBACDEH分析:运用抛物线的定义和平面几何知识来证比较简捷.xy证明:如图. 设AB的中点为E,过A、E、B分别向准线l引垂线AD,EH,BC,垂足为D、H、C,则|AF|=|AD|,|BF|=|BC|∴|AB|
=|AF|+|BF|
=|AD|+|BC|
=2|EH|所以EH是以AB为直径的圆E的半径,且EH⊥l,因而圆E和准线l相切.抛物线的性质特点:(1).抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐进线;(2).抛物线只有一条对称轴,没有对称中心;(3).抛物线只有一个顶点,一个焦点,一条准线;(4).抛物线的离心率是确定的,为1. 探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处. 已知灯口圆的直径为60cm,灯深40cm,求抛物线的标准方程和焦点的位置.实际运用解:如图,在探照灯的轴截面所在平面内建立直角坐标系,使反光镜的顶点(即抛物线的顶点)与原点重合,轴垂直与灯口直径.焦点坐标是由已知条件可得点A的坐标是(40,30),代入方程,得所以所求抛物线的标准方程是即设抛物线的标准方程是 小结:(1)抛物线的简单几何性质
(2)抛物线与椭圆、双曲线几何性质的不同点
(3)应用性质求标准方程的方法和步骤
探讨:习题 P63. 1、2、3 课后作业:敬请
指导!
第二章 第三节生活中的抛物线y2=2pxy2=-2pxx2=2pyx2=-2pyy2 = 2px(p>0)1. 范围:X≥0 ; 抛物线向右上方
和右下方无限延伸. 抛物线的几何性质y2 = 2px(p>0)2. 对称性:抛物线关于x轴对称. 抛物线的几何性质抛物线的对称轴叫做抛物线的轴. y2 = 2px(p>0)抛物线和它的轴的交点叫做抛物线的顶点. 3. 顶点:4. 离心率:e =1 抛物线的几何性质y2=2px
(p>0)Oy2=-2px
(p>0)x2=2py
(p>0)x2=-2py
(p>0)(0,0)(0,0)(0,0)(0,0)x轴x轴y轴y轴xyFlxyOFlDD3解:根据题意,可设它的标准方程为
y2 =2px ( p > 0 ).因为点M在抛物线上,所以即 p=2.因此所求方程为y2 =4x.思考(2)你有办法画出它的图像?将已知方程变形为y= 2 ,根据 y =2 , 计算抛物线在x 0的范围内几个点的坐标,得用光滑的曲线连结这些点;然后利用抛物线的对称性作出另一部分图像.过焦点且垂直于对称轴的直线被抛物线截得的线段AB叫做抛物线的通径.连结:过抛物线 的焦点F作垂直与轴的直线,交抛物线于A、B两点,则以AB 为直径的圆的方程是AB通径长为2p.CD拓展:xyOFABB’A’ 引伸: 过抛物线y2=2px的焦点F任作一条直线m,交这抛物线于A、B两点,求证:以AB为直径的圆和这抛物线的准线相切.OFBACDEH分析:运用抛物线的定义和平面几何知识来证比较简捷.xy证明:如图. 设AB的中点为E,过A、E、B分别向准线l引垂线AD,EH,BC,垂足为D、H、C,则|AF|=|AD|,|BF|=|BC|∴|AB|
=|AF|+|BF|
=|AD|+|BC|
=2|EH|所以EH是以AB为直径的圆E的半径,且EH⊥l,因而圆E和准线l相切.抛物线的性质特点:(1).抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐进线;(2).抛物线只有一条对称轴,没有对称中心;(3).抛物线只有一个顶点,一个焦点,一条准线;(4).抛物线的离心率是确定的,为1. 探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处. 已知灯口圆的直径为60cm,灯深40cm,求抛物线的标准方程和焦点的位置.实际运用解:如图,在探照灯的轴截面所在平面内建立直角坐标系,使反光镜的顶点(即抛物线的顶点)与原点重合,轴垂直与灯口直径.焦点坐标是由已知条件可得点A的坐标是(40,30),代入方程,得所以所求抛物线的标准方程是即设抛物线的标准方程是 小结:(1)抛物线的简单几何性质
(2)抛物线与椭圆、双曲线几何性质的不同点
(3)应用性质求标准方程的方法和步骤
探讨:习题 P63. 1、2、3 课后作业:敬请
指导!
