寒假查漏补缺检测卷-数学六年级上册苏教版(含解析)
文档属性
| 名称 | 寒假查漏补缺检测卷-数学六年级上册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 391.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 15:47:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
寒假查漏补缺检测卷-数学六年级上册苏教版
一、选择题
1.把11∶15的前项增加22,要使比值不变,后项应该( )。
A.加上22 B.乘22 C.除以22 D.乘3
2.甲乙两根长都是1米的彩带,甲截去,乙截去米,剩下的彩带相比较,( )。
A.甲长 B.乙长 C.一样长 D.无法确定
3.商店出售两件不同的商品,售价是180元,按进价计算,一件赚了20%,另一件亏了20%,则售出这两件商品( )。
A.不赚不亏 B.亏15元 C.赚15元 D.赚18元
4.一个长方体和一个正方体的底面积相等,如果长方体的高是正方体棱长的2倍,那么,长方体与正方体的体积比是( )。
A.2∶1 B.1∶2 C.1∶1 D.4∶1
5.庆元旦,一件商品八折销售,活动过后提价( ),该商品可回到活动前的价格。
A. B. C. D.
6.下面说法正确的有( )个。
(1)泰州实验学校“幸福球”活动中,六年级有一场足球比赛3∶0,说明比的后项可以是0;
(2)两根同样长的绳子,第一根剪去,第二根剪去米,第一根剩下的绳长,说明原来绳比1米短;
(3)一个正方体的棱长扩大到原来的2倍,体积就扩大到原来的6倍;
(4)商场同时卖出两件上衣,每件都以600元出售,若按成本计算,其中一件盈利25%,另一件亏本25%,则在这次买卖中,商场亏了80元。
A.1 B.2 C.3 D.4
二、填空题
7.在、3.149、π、315%这些数中,最大的数是( ),最小的数是( )。
8.李东从甲地步行到乙地,行了全程的,正好行了480米,全程有( )米,再行( )米到达全程的中点。
9.王叔叔因一项科技发明,获得了5000元奖金。按规定应缴纳20%的个人所得税,王叔叔实际获得奖金( )元;他把实得奖金存入银行,定期三年,年利率是2.75%,到期他应得到本金和利息一共( )元。
10.永新面粉厂小时可以加工面粉吨,照这样计算,1小时可以加工面粉( )吨,加工1吨面粉需要( )小时。
11.男、女生的人数比为2∶3,那么男生人数相当于女生人数的( ),女生人数相当于全班人数的( )(在括号内填写分数)。
12.一个正方形的边长增加它的后,得到的新正方形的周长是48厘米,原正方形的边长是( )厘米。
三、判断题
13.一个数(0除外)乘真分数,积一定小于这个数. ( )
14.一件衣服,先提价,再降价,结果与原价一样多.( )
15.体积单位比面积单位大。( )
16.一件上衣标价100元,商店打八八折出售,买这件上衣需要80元.( )
17.长方体和正方体都有8条棱、12个顶点和6个面.( )
四、计算题
18.直接写出得数。
0.33= 0.01×4.3= ×0÷= =
2.11+79%= 0.42-0.32= (4+)÷4= ×3÷×3=
19.计算下面各题。(能简算的要简算)
2.5×4÷×4 4.96×[4.55÷(2-1.09)]
2.3-4.05+7.7+5.95 46×75%+64÷-7.5
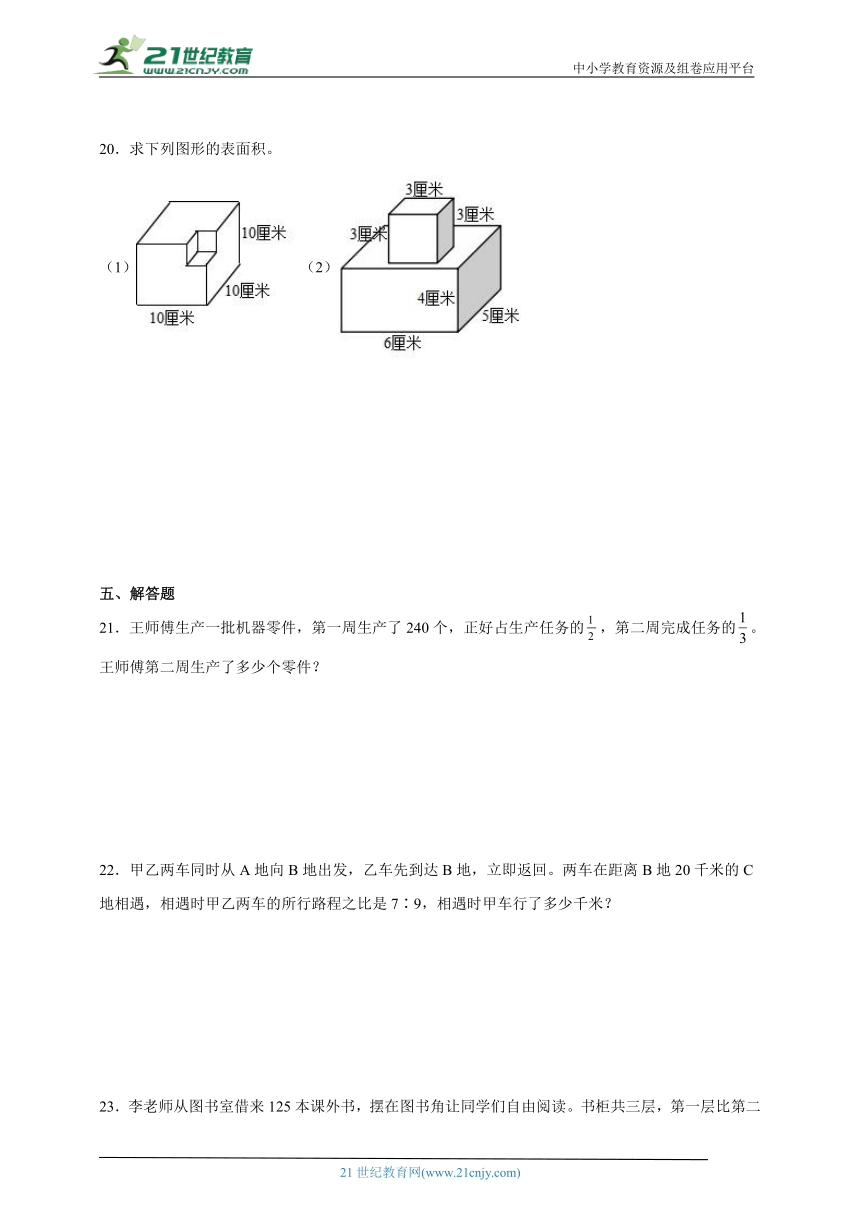
20.求下列图形的表面积。
(1)(2)
五、解答题
21.王师傅生产一批机器零件,第一周生产了240个,正好占生产任务的,第二周完成任务的。王师傅第二周生产了多少个零件?
22.甲乙两车同时从A地向B地出发,乙车先到达B地,立即返回。两车在距离B地20千米的C地相遇,相遇时甲乙两车的所行路程之比是7∶9,相遇时甲车行了多少千米?
23.李老师从图书室借来125本课外书,摆在图书角让同学们自由阅读。书柜共三层,第一层比第二层多12本,第二层比第三层少20本。第三层有多少本书?
24.王老师准备买一辆汽车,如果用现金一次性付款可以打九五折,如果分期付款购买需要加价。他计算后发现,分期付款比现金一次性付款多了19500元,这辆汽车原价是多少元?
25.一个长方体游泳池,长80米,宽20米,深1.8米。在距池口0.3米处有一圈水位警戒线。
(1)在池的四壁和底面贴瓷砖。贴瓷砖的面积是多少?
(2)如果将水放至警戒水位线,需要多少立方米水?
26.甲、乙两个长方体水箱的底面积分别是150平方厘米和100平方厘米,甲水箱中水深40厘米。乙水箱是空的。现在将甲水箱中的一部分水倒入乙水箱,使这两个水箱的水面高度相等。这时水面高是多少厘米?
参考答案:
1.D
【分析】由于前项增加22,此时的前项变为:11+22=33,根据比的性质:比的前项和后项同时乘或除以同一个数(0除外)比值不变,由于11×3=33,即前项乘3,后项也应该乘3,此时后项是:15×3=45,或者增加:45-15=30,据此即可选择。
【详解】11+22=33
33÷11=3
15×3=45
45-15=30
所以后项应该乘3或者增加30。
故答案为:D
【点睛】本题主要考查比的基本性质,熟练掌握比的基本性质并灵活运用。
2.C
【分析】求出甲乙两根彩带剩下的长度比较,甲截去,将甲的长度看做单位“1”,根据求一个数的几分之几是多少用乘法,即可求出截去的长度,然后求出剩下的长度;乙截去米,即用原长度减去截去的长度,即可求出剩下的长度,据此解答即可。
【详解】1-1×
=1-
=(米)
1-=(米)
=
所以剩下的彩带长度相等
故答案为:C
【点睛】本题考查分数有无单位的区别,以及求一个数的几分之几用乘法,要重点掌握。
3.B
【分析】将进价看作单位“1”,分别用两件商品的售价÷对应百分率,求出进价,相加,再求出两件商品总的售价,进行比较,求差即可。
【详解】180÷(1+20%)+180÷(1-20%)
=180÷1.2+180÷0.8
=150+225
=375(元)
180+180=360(元)
375>360
375-360=15(元)
商店出售两件不同的商品,售价是180元,按进价计算,一件赚了20%,另一件亏了20%,则售出这两件商品亏15元。
故答案为:B
【点睛】解答本题的关键是确定单位“1”。部分数量÷对应百分比=整体数量。
4.A
【分析】根据长方体和正方体的体积公式:体积=底面积×高,再根据因数与积的变化规律,一个因数不变,另一个因数扩大2倍,积也扩大2倍,据此解答。
【详解】个长方体和正方体的底面积相等,长方体的高是正方体棱长的2倍,根据长方体和正方体的体积公式:底面积×高;长方体的体积是正方体的2倍;
即长方体与正方体的体积比是2∶1。
一个长方体和一个正方体的底面积相等,如果长方体的高是正方体棱长的2倍,那么,长方体与正方体的体积比是2∶1。
故答案为:A
【点睛】本题考查长方体和正方体体积公式的应用,关键是熟记公式,灵活运用。
5.C
【分析】打八折就是现价是原价的80%,把原价看作单位“1”,现价比原价便宜了(1-80%),再用便宜的部分除以促销价,乘100%,即可解答。
【详解】八折就是现价是原价的80%。
(1-80%)÷80%×100%
=20%÷80%×100%
=0.25×100%
=25%
庆元旦,一件商品八折销售,活动过后提价25%,该商品可回到活动前的价格。
故答案为:C
【点睛】本题考查折扣问题以及求一个数是另一个数的百分之几,用除法解答。
6.B
【分析】(1)赛场上的比分是一种记录分数的形式,据此判断;
(2)第一根剩下的长,则第一根用去的短,据此结合分数的意义判断;
(3)正方体的体积=棱长×棱长×棱长,据此结合给出的信息判断;
(4)第一件成本是600÷(1+25%),第二件成本是600÷(1-25%),据此分别算出两件衣服的成本,再比较总成本和总售价,即可得到亏了还是赚了,再求出两者之差即可得到亏或赚了多少元。
【详解】(1)比赛中的3∶0是一种记录比分的形式,不是我们数学概念中的比,比的后项不能为0;
(2)第一根剩下的长,说明第一根剪去的比第二根减去的短,即这根绳子的比米短,则这根绳子原来的长度比1米短;
(3)一个正方体的棱长扩大到原来的2倍,体积就扩大到原来的2×2×2=8倍;
(4)600÷(1+25%)
=600÷1.25
=480(元)
600÷(1-25%)
=600÷0.75
=800(元)
总成本:480+800=1280(元)
总售价:600+600=1200(元)
1280-1000=280(元)
则在这次买卖中,商场亏了80元。
(2)(4)说法正确。
故答案为:B
【点睛】掌握比的意义、分数的意义、正方体的体积公式及求利润的方法是解答本题的关键。
7. π
【分析】首先把、315%化成小数,再求出π的近似值,然后再根据小数的大小比较方法,先看它们的整数部分,整数部分大的那个数大;如果整数部分相同,十分位上的数大的那个数大;如果十分位上的数也相同,百分位上的数大的那个数大,解答即可。
【详解】≈3.2857
π≈3.1416
315%=3.15
因为3.2857>3.15>3.149>3.1416
所以在、3.149、π、315%这些数中,最大的数是,最小的数是π。
【点睛】此题考查了分数、百分数、小数的大小比较,同时还考查了分数、百分数、小数的互化。
8. 1200 120
【分析】把甲地到乙地的全程看作单位“1”,根据分数除法的意义,用480米除以,就是从甲地到乙地的全程;根据分数乘法的意义,用全程乘,再减已行的480米,据此解答。
【详解】480÷=1200(米)
1200×-480
=600-480
=120(米)
全程有1200米,再行120米到达全程的中点。
【点睛】已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率;求一个数的几分之几是多少,用这个数乘分率。
9. 4000 4330
【分析】将5000元奖金看成单位“1”,应缴纳20%的个人所得税,则实际得到1-20%=80%,根据分数乘法的意义,用5000×80%求出实际获得的奖金;利息=本金×利率×时间,代入数据求出利息,最后加上本金即可。
【详解】5000×(1-20%)
=5000×0.8
=4000(元)
4000×2.75%×3+4000
=110×3+4000
=330+4000
=4330(元)
即王叔叔实际获得奖金4000元,把实得奖金存入银行,定期三年,年利率是2.75%,到期他应得到本金和利息一共4330元。
【点睛】本题考查税率、利率问题,理解税率及利息结算方法是解题的关键。
10.
【分析】求1小时能加工面粉的吨数,平均分的是面粉的总吨数,求加工1吨面粉要用的时间,平均分的是总时间,都用除法计算。
【详解】÷
=×
=(吨)
÷
=×
=(小时)
永新面粉厂小时可以加工面粉吨,照这样计算,1小时可以加工面粉吨,加工1吨面粉需要小时。
【点睛】解答本题的关键是弄清楚平均分的是哪一个量,就要这个量除以另一个量即可。
11.
【分析】男、女生人数比为2∶3,可以把男生人数看作2份,女生人数看作3份,男生人数相当于女生人数的几分之几,用男生人数的份数除以女生人数的份数即可;全班人数是(2+3)份,用女生人数的份数除以全班人数的份数即可解答。
【详解】根据分析可得,把男生人数看作2份,女生人数看作3份。
2÷3=
3÷(2+3)
=3÷5
=
男、女生的人数比为2∶3,那么男生人数相当于女生人数的,女生人数相当于全班人数的。
【点睛】解答本题主要依据分数与除法的关系以及比的意义进行解答。
12.9
【分析】根据正方形周长公式:周长=边长×4;边长=周长÷4,代入数据,求出增加后正方形的边长;再把原正方形边长看作单位“1”,增加它的后,增加后的边长是原正方形边长的(1+),求单位“1”,再用增加后正方形的边长÷(1+),求出原正方形的边长。
【详解】48÷4÷(1+)
=12÷(1+)
=12÷
=12×
=9(厘米)
原正方形边长是9厘米。
【点睛】利用已知一个数的几分之几是多少,求这个数,以及正方形周长公式的应用。
13.√
【详解】根据真分数的意义,分数的分子比分母小的分数叫做真分数,真分数小于1。一个数(0除外)乘小于1的数,积一定小于这个数。据此判断即可。
【解答】解:一个数(0除外)乘真分数,所得的积一定小于这个数。此说法正确。
如:
故答案为:。
【点评】此题考查的目的是掌握不用计算判断因数与积的大小关系的方法。
14.×
【解答】解:1×(1+)×(1﹣)
=1××
=
<1
即现价低于原价。
故答案为:×。
15.×
【详解】体积和面积不是同一种量,所以体积单位和面积单位无法比较大小,原题说法错误。
故答案为:×
16.×
【分析】打八八折是指现价是原价的88%,把原价看成单位“1”,用乘法求出它的88%就是现价,再判断即可.
【详解】100×88%=88(元)
答:买这件上衣需要88元。
故答案为:×
【点睛】此题是百分数的实际应用题,打几折就是百分之几十。
17.×
【解析】略
18.0.027;0.043;0;;
2.9;0.07;1;9
【详解】略
19.100;24.8
11.9;75
【分析】先将除法变为乘法,再根据乘法结合律进行简算;
先算小括号里的减法,再算中括号里的除法,最后算括号外的乘法;
根据加法交换律、结合律进行简算;
把除法化成乘法,再运用乘法分配律进行简算。
【详解】2.5×4÷×4
=2.5×4××4
=(2.5×4)×(×4)
=10×10
=100
4.96×[4.55÷(2-1.09)]
=4.96×[4.55÷0.91]
=4.96×5
=24.8
2.3-4.05+7.7+5.95
=2.3+7.7+5.95-4.05
=(2.3+7.7)+(5.95-4.05)
=10+1.9
=11.9
46×75%+64÷-7.5
=46×75%+64×-0.75×10
=(46+64-10)×75%
=100×75%
=75
20.(1)600平方厘米
(2)184平方厘米
【分析】(1)少了三个小正方体的面,同时又添加了三个小正方体的面,图形的表面积=棱长×棱长×6;
(2)长方体的表面积+正方体四个面的面积,其中长方体的表面积=(长×宽+长×高+宽×高)×2,正方体四个面的面积=棱长×棱长×4,据此解答。
【详解】(1)10×10×6
=100×6
=600(平方厘米)
(2)(6×5+6×4+5×4)×2+3×3×4
=148+36
=184(平方厘米)
21.160个
【分析】将这批零件总数看作单位“1”,先用240除以,求出这批零件总数,再乘即可求出第二周生产的个数。
【详解】240÷×
=480×
=160(个)
答:王师傅第二周生产了160个零件。
【点睛】已知一个数的几分之几是多少,求这个数,用除法计算;求一个数的几分之几是多少,用乘法计算。
22.140千米
【分析】据题意分析,两车相遇时,乙车比甲车多走了(20×2)千米,相遇时甲乙两车的所行路程之比是7∶9,可将甲车行驶的路程看作7份,乙车行驶的路程看作9份,用两车相遇时,两车行驶的路程之差除以(9-7),可求出一份代表的路程,再乘7即可得出相遇时,甲车行的千米数。
【详解】由分析可得:
20×2÷(9-7)×7
=40÷2×7
=20×7
=140(千米)
答:相遇时甲车行了140千米。
【点睛】本题主要考查了行程问题中速度、时间、路程的关系,同时要能通过对题的分析求出两车的路程差,再按照路程比求出每份数。
23.51本
【分析】根据题意,可以设第二层有x本书,第一层比第二层多12本,则第一层表示为(x+12)本,第二层比第三层少20本,则第三层有(x+20)本书,可得数量关系:第一层书的本数+第二层书的本数+第三层书的本数=125本,据此列方程即可。
【详解】由分析可得:
解:设第二层有x本书,
x+12+x+20+x=125
3x+32=125
3x+32-32=125-32
3x=93
3x÷3=93÷3
x=31
31+20=51(本)
答:第三层有51本。
【点睛】本题考查了简单的列方程解应用题,关键是找准等量关系,根据题中已知条件写出等量关系式即可。
24.150000元
【分析】通过题意,可以设该汽车原价是x元,九五折,指的是原价的95%,把原价看作单位“1”,求一个数的百分之几是多少用乘法,根据价格公式,原价×折扣=现在的售价,即打九五折可以表示为95%x元,加价,也是原价看作单位“1”,即需要付(1+8%)x元,等量关系式为:分期付款付的钱数-用现金一次性付款的钱数=19500元,据此列方程解答即可。
【详解】由分析可得:
解:设该汽车原价是x元,
(1+8%)x-95%x=19500
1.08x-0.95x=19500
0.13x=19500
0.13x÷0.13=19500÷0.13
x=150000
答:这辆汽车原价是150000元。
【点睛】本题考查了简单的列方程解应用题,关键是找准等量关系,根据题中已知条件写出等量关系式即可。
25.(1)1960平方米
(2)2400立方米
【分析】(1)在池的四壁和底面贴瓷砖,则相当于求长方体泳池的5个面的面积,根据长方体的表面积公式:长×宽+(长×高+宽×高)×2,把数代入公式即可求解;
(2)由于将水放至警戒水位线,则此时水的告诉是:1.8-0.3=1.5(米),根据长方体的体积公式:长×宽×高,把数代入公式即可求出需要多少立方米的水。
【详解】(1)80×20+(80×1.8+20×1.8)×2
=1600+(144+36)×2
=1600+180×2
=1600+360
=1960(平方米)
答:贴瓷砖的面积是1960平方米。
(2)80×20×(1.8-0.3)
=1600×1.5
=2400(立方米)
答:需要2400立方米的水。
【点睛】本题主要考查长方体的表面积和长方体的体积公式,熟练掌握它们的公式并灵活运用。
26.24厘米
【分析】根据长方体体积公式:体积=底面积×高,代入数据,求出甲水箱水的体积;甲、乙两个水箱的体积和等于原来甲水箱的体积,高=体积÷底面积;用甲水箱原来的体积除以甲、乙两水箱的底面积和,即可求出这时水面的高度,据此解答。
【详解】150×40÷(150+100)
=6000÷250
=24(厘米)
答:这时水面高是24厘米。
【点睛】解答本题的关键明确两个水箱的水面高度相同,两个水箱的体积和等于原来甲水箱的体积。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
寒假查漏补缺检测卷-数学六年级上册苏教版
一、选择题
1.把11∶15的前项增加22,要使比值不变,后项应该( )。
A.加上22 B.乘22 C.除以22 D.乘3
2.甲乙两根长都是1米的彩带,甲截去,乙截去米,剩下的彩带相比较,( )。
A.甲长 B.乙长 C.一样长 D.无法确定
3.商店出售两件不同的商品,售价是180元,按进价计算,一件赚了20%,另一件亏了20%,则售出这两件商品( )。
A.不赚不亏 B.亏15元 C.赚15元 D.赚18元
4.一个长方体和一个正方体的底面积相等,如果长方体的高是正方体棱长的2倍,那么,长方体与正方体的体积比是( )。
A.2∶1 B.1∶2 C.1∶1 D.4∶1
5.庆元旦,一件商品八折销售,活动过后提价( ),该商品可回到活动前的价格。
A. B. C. D.
6.下面说法正确的有( )个。
(1)泰州实验学校“幸福球”活动中,六年级有一场足球比赛3∶0,说明比的后项可以是0;
(2)两根同样长的绳子,第一根剪去,第二根剪去米,第一根剩下的绳长,说明原来绳比1米短;
(3)一个正方体的棱长扩大到原来的2倍,体积就扩大到原来的6倍;
(4)商场同时卖出两件上衣,每件都以600元出售,若按成本计算,其中一件盈利25%,另一件亏本25%,则在这次买卖中,商场亏了80元。
A.1 B.2 C.3 D.4
二、填空题
7.在、3.149、π、315%这些数中,最大的数是( ),最小的数是( )。
8.李东从甲地步行到乙地,行了全程的,正好行了480米,全程有( )米,再行( )米到达全程的中点。
9.王叔叔因一项科技发明,获得了5000元奖金。按规定应缴纳20%的个人所得税,王叔叔实际获得奖金( )元;他把实得奖金存入银行,定期三年,年利率是2.75%,到期他应得到本金和利息一共( )元。
10.永新面粉厂小时可以加工面粉吨,照这样计算,1小时可以加工面粉( )吨,加工1吨面粉需要( )小时。
11.男、女生的人数比为2∶3,那么男生人数相当于女生人数的( ),女生人数相当于全班人数的( )(在括号内填写分数)。
12.一个正方形的边长增加它的后,得到的新正方形的周长是48厘米,原正方形的边长是( )厘米。
三、判断题
13.一个数(0除外)乘真分数,积一定小于这个数. ( )
14.一件衣服,先提价,再降价,结果与原价一样多.( )
15.体积单位比面积单位大。( )
16.一件上衣标价100元,商店打八八折出售,买这件上衣需要80元.( )
17.长方体和正方体都有8条棱、12个顶点和6个面.( )
四、计算题
18.直接写出得数。
0.33= 0.01×4.3= ×0÷= =
2.11+79%= 0.42-0.32= (4+)÷4= ×3÷×3=
19.计算下面各题。(能简算的要简算)
2.5×4÷×4 4.96×[4.55÷(2-1.09)]
2.3-4.05+7.7+5.95 46×75%+64÷-7.5
20.求下列图形的表面积。
(1)(2)
五、解答题
21.王师傅生产一批机器零件,第一周生产了240个,正好占生产任务的,第二周完成任务的。王师傅第二周生产了多少个零件?
22.甲乙两车同时从A地向B地出发,乙车先到达B地,立即返回。两车在距离B地20千米的C地相遇,相遇时甲乙两车的所行路程之比是7∶9,相遇时甲车行了多少千米?
23.李老师从图书室借来125本课外书,摆在图书角让同学们自由阅读。书柜共三层,第一层比第二层多12本,第二层比第三层少20本。第三层有多少本书?
24.王老师准备买一辆汽车,如果用现金一次性付款可以打九五折,如果分期付款购买需要加价。他计算后发现,分期付款比现金一次性付款多了19500元,这辆汽车原价是多少元?
25.一个长方体游泳池,长80米,宽20米,深1.8米。在距池口0.3米处有一圈水位警戒线。
(1)在池的四壁和底面贴瓷砖。贴瓷砖的面积是多少?
(2)如果将水放至警戒水位线,需要多少立方米水?
26.甲、乙两个长方体水箱的底面积分别是150平方厘米和100平方厘米,甲水箱中水深40厘米。乙水箱是空的。现在将甲水箱中的一部分水倒入乙水箱,使这两个水箱的水面高度相等。这时水面高是多少厘米?
参考答案:
1.D
【分析】由于前项增加22,此时的前项变为:11+22=33,根据比的性质:比的前项和后项同时乘或除以同一个数(0除外)比值不变,由于11×3=33,即前项乘3,后项也应该乘3,此时后项是:15×3=45,或者增加:45-15=30,据此即可选择。
【详解】11+22=33
33÷11=3
15×3=45
45-15=30
所以后项应该乘3或者增加30。
故答案为:D
【点睛】本题主要考查比的基本性质,熟练掌握比的基本性质并灵活运用。
2.C
【分析】求出甲乙两根彩带剩下的长度比较,甲截去,将甲的长度看做单位“1”,根据求一个数的几分之几是多少用乘法,即可求出截去的长度,然后求出剩下的长度;乙截去米,即用原长度减去截去的长度,即可求出剩下的长度,据此解答即可。
【详解】1-1×
=1-
=(米)
1-=(米)
=
所以剩下的彩带长度相等
故答案为:C
【点睛】本题考查分数有无单位的区别,以及求一个数的几分之几用乘法,要重点掌握。
3.B
【分析】将进价看作单位“1”,分别用两件商品的售价÷对应百分率,求出进价,相加,再求出两件商品总的售价,进行比较,求差即可。
【详解】180÷(1+20%)+180÷(1-20%)
=180÷1.2+180÷0.8
=150+225
=375(元)
180+180=360(元)
375>360
375-360=15(元)
商店出售两件不同的商品,售价是180元,按进价计算,一件赚了20%,另一件亏了20%,则售出这两件商品亏15元。
故答案为:B
【点睛】解答本题的关键是确定单位“1”。部分数量÷对应百分比=整体数量。
4.A
【分析】根据长方体和正方体的体积公式:体积=底面积×高,再根据因数与积的变化规律,一个因数不变,另一个因数扩大2倍,积也扩大2倍,据此解答。
【详解】个长方体和正方体的底面积相等,长方体的高是正方体棱长的2倍,根据长方体和正方体的体积公式:底面积×高;长方体的体积是正方体的2倍;
即长方体与正方体的体积比是2∶1。
一个长方体和一个正方体的底面积相等,如果长方体的高是正方体棱长的2倍,那么,长方体与正方体的体积比是2∶1。
故答案为:A
【点睛】本题考查长方体和正方体体积公式的应用,关键是熟记公式,灵活运用。
5.C
【分析】打八折就是现价是原价的80%,把原价看作单位“1”,现价比原价便宜了(1-80%),再用便宜的部分除以促销价,乘100%,即可解答。
【详解】八折就是现价是原价的80%。
(1-80%)÷80%×100%
=20%÷80%×100%
=0.25×100%
=25%
庆元旦,一件商品八折销售,活动过后提价25%,该商品可回到活动前的价格。
故答案为:C
【点睛】本题考查折扣问题以及求一个数是另一个数的百分之几,用除法解答。
6.B
【分析】(1)赛场上的比分是一种记录分数的形式,据此判断;
(2)第一根剩下的长,则第一根用去的短,据此结合分数的意义判断;
(3)正方体的体积=棱长×棱长×棱长,据此结合给出的信息判断;
(4)第一件成本是600÷(1+25%),第二件成本是600÷(1-25%),据此分别算出两件衣服的成本,再比较总成本和总售价,即可得到亏了还是赚了,再求出两者之差即可得到亏或赚了多少元。
【详解】(1)比赛中的3∶0是一种记录比分的形式,不是我们数学概念中的比,比的后项不能为0;
(2)第一根剩下的长,说明第一根剪去的比第二根减去的短,即这根绳子的比米短,则这根绳子原来的长度比1米短;
(3)一个正方体的棱长扩大到原来的2倍,体积就扩大到原来的2×2×2=8倍;
(4)600÷(1+25%)
=600÷1.25
=480(元)
600÷(1-25%)
=600÷0.75
=800(元)
总成本:480+800=1280(元)
总售价:600+600=1200(元)
1280-1000=280(元)
则在这次买卖中,商场亏了80元。
(2)(4)说法正确。
故答案为:B
【点睛】掌握比的意义、分数的意义、正方体的体积公式及求利润的方法是解答本题的关键。
7. π
【分析】首先把、315%化成小数,再求出π的近似值,然后再根据小数的大小比较方法,先看它们的整数部分,整数部分大的那个数大;如果整数部分相同,十分位上的数大的那个数大;如果十分位上的数也相同,百分位上的数大的那个数大,解答即可。
【详解】≈3.2857
π≈3.1416
315%=3.15
因为3.2857>3.15>3.149>3.1416
所以在、3.149、π、315%这些数中,最大的数是,最小的数是π。
【点睛】此题考查了分数、百分数、小数的大小比较,同时还考查了分数、百分数、小数的互化。
8. 1200 120
【分析】把甲地到乙地的全程看作单位“1”,根据分数除法的意义,用480米除以,就是从甲地到乙地的全程;根据分数乘法的意义,用全程乘,再减已行的480米,据此解答。
【详解】480÷=1200(米)
1200×-480
=600-480
=120(米)
全程有1200米,再行120米到达全程的中点。
【点睛】已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率;求一个数的几分之几是多少,用这个数乘分率。
9. 4000 4330
【分析】将5000元奖金看成单位“1”,应缴纳20%的个人所得税,则实际得到1-20%=80%,根据分数乘法的意义,用5000×80%求出实际获得的奖金;利息=本金×利率×时间,代入数据求出利息,最后加上本金即可。
【详解】5000×(1-20%)
=5000×0.8
=4000(元)
4000×2.75%×3+4000
=110×3+4000
=330+4000
=4330(元)
即王叔叔实际获得奖金4000元,把实得奖金存入银行,定期三年,年利率是2.75%,到期他应得到本金和利息一共4330元。
【点睛】本题考查税率、利率问题,理解税率及利息结算方法是解题的关键。
10.
【分析】求1小时能加工面粉的吨数,平均分的是面粉的总吨数,求加工1吨面粉要用的时间,平均分的是总时间,都用除法计算。
【详解】÷
=×
=(吨)
÷
=×
=(小时)
永新面粉厂小时可以加工面粉吨,照这样计算,1小时可以加工面粉吨,加工1吨面粉需要小时。
【点睛】解答本题的关键是弄清楚平均分的是哪一个量,就要这个量除以另一个量即可。
11.
【分析】男、女生人数比为2∶3,可以把男生人数看作2份,女生人数看作3份,男生人数相当于女生人数的几分之几,用男生人数的份数除以女生人数的份数即可;全班人数是(2+3)份,用女生人数的份数除以全班人数的份数即可解答。
【详解】根据分析可得,把男生人数看作2份,女生人数看作3份。
2÷3=
3÷(2+3)
=3÷5
=
男、女生的人数比为2∶3,那么男生人数相当于女生人数的,女生人数相当于全班人数的。
【点睛】解答本题主要依据分数与除法的关系以及比的意义进行解答。
12.9
【分析】根据正方形周长公式:周长=边长×4;边长=周长÷4,代入数据,求出增加后正方形的边长;再把原正方形边长看作单位“1”,增加它的后,增加后的边长是原正方形边长的(1+),求单位“1”,再用增加后正方形的边长÷(1+),求出原正方形的边长。
【详解】48÷4÷(1+)
=12÷(1+)
=12÷
=12×
=9(厘米)
原正方形边长是9厘米。
【点睛】利用已知一个数的几分之几是多少,求这个数,以及正方形周长公式的应用。
13.√
【详解】根据真分数的意义,分数的分子比分母小的分数叫做真分数,真分数小于1。一个数(0除外)乘小于1的数,积一定小于这个数。据此判断即可。
【解答】解:一个数(0除外)乘真分数,所得的积一定小于这个数。此说法正确。
如:
故答案为:。
【点评】此题考查的目的是掌握不用计算判断因数与积的大小关系的方法。
14.×
【解答】解:1×(1+)×(1﹣)
=1××
=
<1
即现价低于原价。
故答案为:×。
15.×
【详解】体积和面积不是同一种量,所以体积单位和面积单位无法比较大小,原题说法错误。
故答案为:×
16.×
【分析】打八八折是指现价是原价的88%,把原价看成单位“1”,用乘法求出它的88%就是现价,再判断即可.
【详解】100×88%=88(元)
答:买这件上衣需要88元。
故答案为:×
【点睛】此题是百分数的实际应用题,打几折就是百分之几十。
17.×
【解析】略
18.0.027;0.043;0;;
2.9;0.07;1;9
【详解】略
19.100;24.8
11.9;75
【分析】先将除法变为乘法,再根据乘法结合律进行简算;
先算小括号里的减法,再算中括号里的除法,最后算括号外的乘法;
根据加法交换律、结合律进行简算;
把除法化成乘法,再运用乘法分配律进行简算。
【详解】2.5×4÷×4
=2.5×4××4
=(2.5×4)×(×4)
=10×10
=100
4.96×[4.55÷(2-1.09)]
=4.96×[4.55÷0.91]
=4.96×5
=24.8
2.3-4.05+7.7+5.95
=2.3+7.7+5.95-4.05
=(2.3+7.7)+(5.95-4.05)
=10+1.9
=11.9
46×75%+64÷-7.5
=46×75%+64×-0.75×10
=(46+64-10)×75%
=100×75%
=75
20.(1)600平方厘米
(2)184平方厘米
【分析】(1)少了三个小正方体的面,同时又添加了三个小正方体的面,图形的表面积=棱长×棱长×6;
(2)长方体的表面积+正方体四个面的面积,其中长方体的表面积=(长×宽+长×高+宽×高)×2,正方体四个面的面积=棱长×棱长×4,据此解答。
【详解】(1)10×10×6
=100×6
=600(平方厘米)
(2)(6×5+6×4+5×4)×2+3×3×4
=148+36
=184(平方厘米)
21.160个
【分析】将这批零件总数看作单位“1”,先用240除以,求出这批零件总数,再乘即可求出第二周生产的个数。
【详解】240÷×
=480×
=160(个)
答:王师傅第二周生产了160个零件。
【点睛】已知一个数的几分之几是多少,求这个数,用除法计算;求一个数的几分之几是多少,用乘法计算。
22.140千米
【分析】据题意分析,两车相遇时,乙车比甲车多走了(20×2)千米,相遇时甲乙两车的所行路程之比是7∶9,可将甲车行驶的路程看作7份,乙车行驶的路程看作9份,用两车相遇时,两车行驶的路程之差除以(9-7),可求出一份代表的路程,再乘7即可得出相遇时,甲车行的千米数。
【详解】由分析可得:
20×2÷(9-7)×7
=40÷2×7
=20×7
=140(千米)
答:相遇时甲车行了140千米。
【点睛】本题主要考查了行程问题中速度、时间、路程的关系,同时要能通过对题的分析求出两车的路程差,再按照路程比求出每份数。
23.51本
【分析】根据题意,可以设第二层有x本书,第一层比第二层多12本,则第一层表示为(x+12)本,第二层比第三层少20本,则第三层有(x+20)本书,可得数量关系:第一层书的本数+第二层书的本数+第三层书的本数=125本,据此列方程即可。
【详解】由分析可得:
解:设第二层有x本书,
x+12+x+20+x=125
3x+32=125
3x+32-32=125-32
3x=93
3x÷3=93÷3
x=31
31+20=51(本)
答:第三层有51本。
【点睛】本题考查了简单的列方程解应用题,关键是找准等量关系,根据题中已知条件写出等量关系式即可。
24.150000元
【分析】通过题意,可以设该汽车原价是x元,九五折,指的是原价的95%,把原价看作单位“1”,求一个数的百分之几是多少用乘法,根据价格公式,原价×折扣=现在的售价,即打九五折可以表示为95%x元,加价,也是原价看作单位“1”,即需要付(1+8%)x元,等量关系式为:分期付款付的钱数-用现金一次性付款的钱数=19500元,据此列方程解答即可。
【详解】由分析可得:
解:设该汽车原价是x元,
(1+8%)x-95%x=19500
1.08x-0.95x=19500
0.13x=19500
0.13x÷0.13=19500÷0.13
x=150000
答:这辆汽车原价是150000元。
【点睛】本题考查了简单的列方程解应用题,关键是找准等量关系,根据题中已知条件写出等量关系式即可。
25.(1)1960平方米
(2)2400立方米
【分析】(1)在池的四壁和底面贴瓷砖,则相当于求长方体泳池的5个面的面积,根据长方体的表面积公式:长×宽+(长×高+宽×高)×2,把数代入公式即可求解;
(2)由于将水放至警戒水位线,则此时水的告诉是:1.8-0.3=1.5(米),根据长方体的体积公式:长×宽×高,把数代入公式即可求出需要多少立方米的水。
【详解】(1)80×20+(80×1.8+20×1.8)×2
=1600+(144+36)×2
=1600+180×2
=1600+360
=1960(平方米)
答:贴瓷砖的面积是1960平方米。
(2)80×20×(1.8-0.3)
=1600×1.5
=2400(立方米)
答:需要2400立方米的水。
【点睛】本题主要考查长方体的表面积和长方体的体积公式,熟练掌握它们的公式并灵活运用。
26.24厘米
【分析】根据长方体体积公式:体积=底面积×高,代入数据,求出甲水箱水的体积;甲、乙两个水箱的体积和等于原来甲水箱的体积,高=体积÷底面积;用甲水箱原来的体积除以甲、乙两水箱的底面积和,即可求出这时水面的高度,据此解答。
【详解】150×40÷(150+100)
=6000÷250
=24(厘米)
答:这时水面高是24厘米。
【点睛】解答本题的关键明确两个水箱的水面高度相同,两个水箱的体积和等于原来甲水箱的体积。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
