等差数列前n项和(1)公开课
图片预览






文档简介
课件17张PPT。2.3 等差数列前n项和(1)知识回顾(3)an=kn+b等差数列 德国古代著名数学家高斯10岁的时候很快就解决了这个问题:1+2+3+…+100=?你知道高斯是怎样算出来的吗?赶快开动脑筋,想一想!导入新课导入新课计算: 1+2+3+ …… +100=?问题一 1 + 2 + 3 +…… 98 + 99 + 1001009998321+++……++M=M=①②首项与末项的和: 1+100=101, 第2项与倒数第2项的和: 2+99=101, 第3项与倒数第3项的和: 3+98=101,
……任意的第k项与倒数第k项的和都等于首项与末项的和;
于是所求的和为:高斯的思路:(1)所求的和可以用首项、末项及项数来表示;上述求解过程带给我们什么
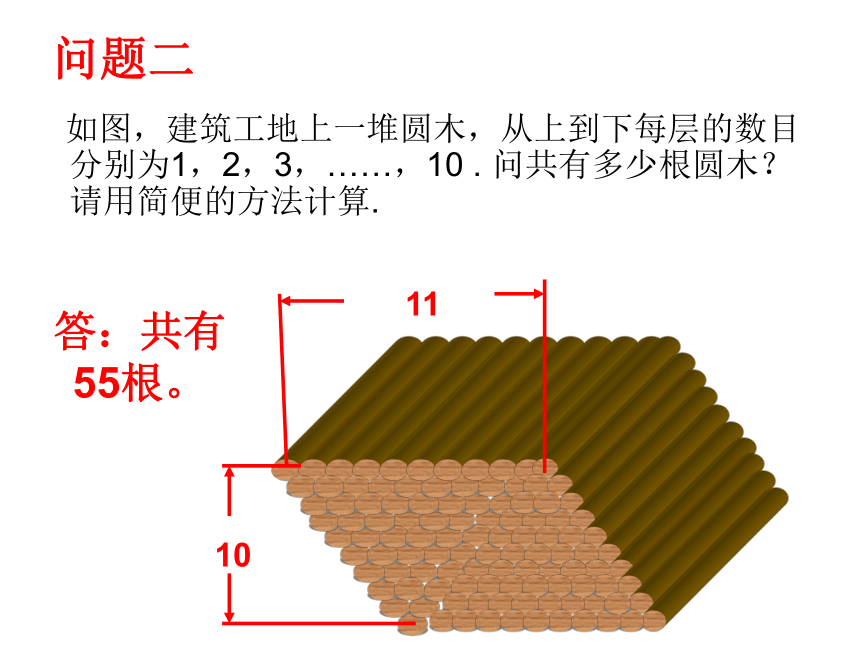
启示呢 (2)任意的第k项与倒数第k项的和都等于首项与末项的和.?计算: 1+2+3+ …… +100=?计算: 1, 2, 3, …… , 100问题二 如图,建筑工地上一堆圆木,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根圆木?请用简便的方法计算.1011答:共有55根。探究发现问题 :如果把两式左右两端相加,将会有什么结果?探究发现倒序相加法求下列等差数列的前n项和Sn(1)1,2,3,4,…,n(2)1,3,5,7,…,2n-1Sn=n2等差数列前n项和公式知三求二解:记等差数列为{an},则有a1=-10,
d=-6-(-10)=4 ,sn代表该数列的前n项和, 变形:若求前多少项和是54呢?公式的应用一 解:根据等差数列前n项和公式:
解得 n1=9 或 n2=-3(舍去)因此等差数列-10,-6,-2,2,...前9项的和是54.变形:等差数列-10,-6,-2,2,...,
前多少项和是54呢?公式的应用一例2 计算:
(1)在1与6之间插入3个数,使这5个数成等差数列,求它们的和.(3)在等差数列{an}中, a1=2 , a17=66 ,求它的前n项和Sn.(2)求等差数列1,4,7,10 ……前15项的和。知三求二之随堂练习1、根据下列各题中的条件,求相应的等差数列{an}的前n项和Sn(1)a1=5, an=95, n=10(2)a1=100, d=-2, n=50(3)a1=14.5, d=0.7, an=32-171知三求二之例3 2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》。某市据此提出了实施“校校通”工程的总目标:从2001年起用10年的时间,在全市中小学建成不同标准的校园网。据测算,2001年该市用于“校校通”工程的经费为500万元。为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元。那么从2001年起的未来10年内,该市在“校校通”工程中的总投入是多少?解:由题意,从2001~2010年,该市每年投入“校校通”工程的经费都比上一年增加50万元。所以,可建立一个等差数列{an},表示从2001年起各年投入的资金,其中
a1=500, d=50,n=10投入资金总额为:
答:从2001~2010年,该市每年投入“校校通”的总资金为7250万元。公式的应用二小结1.公式的推导方法:倒序相加法。3.公式的应用。在公式中有 a1, an, n, d, sn五个量,
已知其中三个可以求出另外两个。作业:课本P46页 习题2.3 A
1(1)(3)
2(2)(4)
32.一个各项均为正整数的等差数列,
其前7项的和为35,求其首项。问题探究:1.在等差数列{an}中
……任意的第k项与倒数第k项的和都等于首项与末项的和;
于是所求的和为:高斯的思路:(1)所求的和可以用首项、末项及项数来表示;上述求解过程带给我们什么
启示呢 (2)任意的第k项与倒数第k项的和都等于首项与末项的和.?计算: 1+2+3+ …… +100=?计算: 1, 2, 3, …… , 100问题二 如图,建筑工地上一堆圆木,从上到下每层的数目分别为1,2,3,……,10 . 问共有多少根圆木?请用简便的方法计算.1011答:共有55根。探究发现问题 :如果把两式左右两端相加,将会有什么结果?探究发现倒序相加法求下列等差数列的前n项和Sn(1)1,2,3,4,…,n(2)1,3,5,7,…,2n-1Sn=n2等差数列前n项和公式知三求二解:记等差数列为{an},则有a1=-10,
d=-6-(-10)=4 ,sn代表该数列的前n项和, 变形:若求前多少项和是54呢?公式的应用一 解:根据等差数列前n项和公式:
解得 n1=9 或 n2=-3(舍去)因此等差数列-10,-6,-2,2,...前9项的和是54.变形:等差数列-10,-6,-2,2,...,
前多少项和是54呢?公式的应用一例2 计算:
(1)在1与6之间插入3个数,使这5个数成等差数列,求它们的和.(3)在等差数列{an}中, a1=2 , a17=66 ,求它的前n项和Sn.(2)求等差数列1,4,7,10 ……前15项的和。知三求二之随堂练习1、根据下列各题中的条件,求相应的等差数列{an}的前n项和Sn(1)a1=5, an=95, n=10(2)a1=100, d=-2, n=50(3)a1=14.5, d=0.7, an=32-171知三求二之例3 2000年11月14日教育部下发了《关于在中小学实施“校校通”工程的通知》。某市据此提出了实施“校校通”工程的总目标:从2001年起用10年的时间,在全市中小学建成不同标准的校园网。据测算,2001年该市用于“校校通”工程的经费为500万元。为了保证工程的顺利实施,计划每年投入的资金都比上一年增加50万元。那么从2001年起的未来10年内,该市在“校校通”工程中的总投入是多少?解:由题意,从2001~2010年,该市每年投入“校校通”工程的经费都比上一年增加50万元。所以,可建立一个等差数列{an},表示从2001年起各年投入的资金,其中
a1=500, d=50,n=10投入资金总额为:
答:从2001~2010年,该市每年投入“校校通”的总资金为7250万元。公式的应用二小结1.公式的推导方法:倒序相加法。3.公式的应用。在公式中有 a1, an, n, d, sn五个量,
已知其中三个可以求出另外两个。作业:课本P46页 习题2.3 A
1(1)(3)
2(2)(4)
32.一个各项均为正整数的等差数列,
其前7项的和为35,求其首项。问题探究:1.在等差数列{an}中
