用导数判断函数的单调性(新人教B选修1-1)
文档属性
| 名称 | 用导数判断函数的单调性(新人教B选修1-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 24.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-27 00:00:00 | ||
图片预览





文档简介
课件16张PPT。3.3.1利用导数判断函数的单调性(一)学习目标2.能应用求导方法判定函数的增减性及求出
函数的单调区间;领会学习导数的作用.1.掌握用求导数判断函数单调性的方法,并
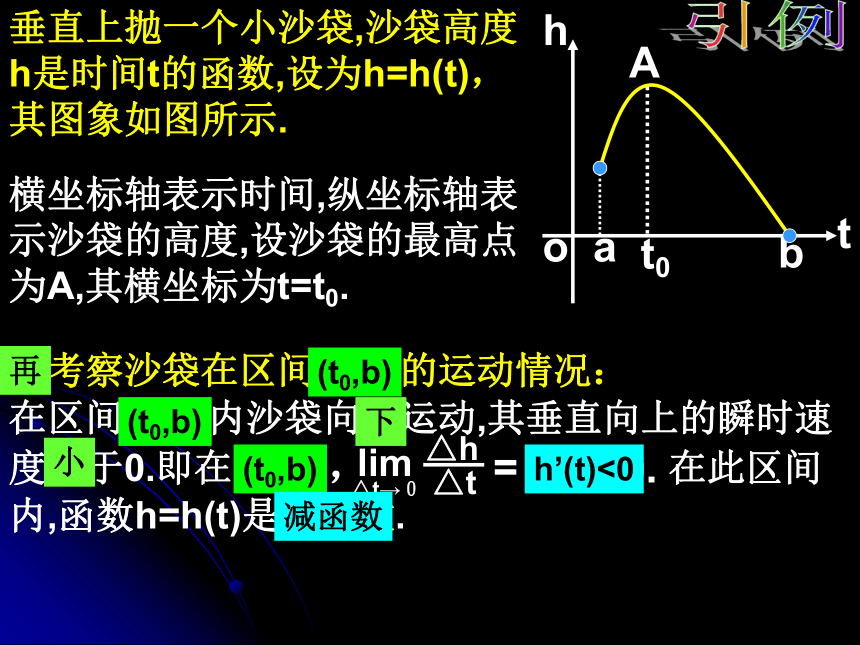
会灵活应用;引例垂直上抛一个小沙袋,沙袋高度
h是时间t的函数,设为h=h(t),
其图象如图所示.横坐标轴表示时间,纵坐标轴表
示沙袋的高度,设沙袋的最高点
为A,其横坐标为t=t0.先考察沙袋在区间(a,t0)的运动情况:在区间(a,t0)内沙袋向上运动,其垂直向上的瞬时速
度大于0.即在(a,t0), 在此区间
内,函数h=h(t)是增函数.(t0,b)下小(t0,b)h’(t)<0减函数用导数判断函数单调性的法则:1.如果在(a,b)内,f ’(x)>0,则f(x)在此区间是增
函数,(a,b)为f(x)的单调增区间;2.如果在(a,b)内,f ’(x)<0,则f(x)在此区间是减
函数,(a,b)为f(x)的单调减区间;用函数曲线的切线的斜率来理解这个法则:当切线斜率为正时,切线的
倾斜角小于900, 函数曲线
呈上升状态;当切线斜率为
负时,函数曲线呈下降状态.对法则的理解:该法则只说明f ′ (x)>0(或 <0)是函数f(x)为增
(减)函数的充分条件但并不是必要的.例如,函数y=x3在实数集内是增函数,但有
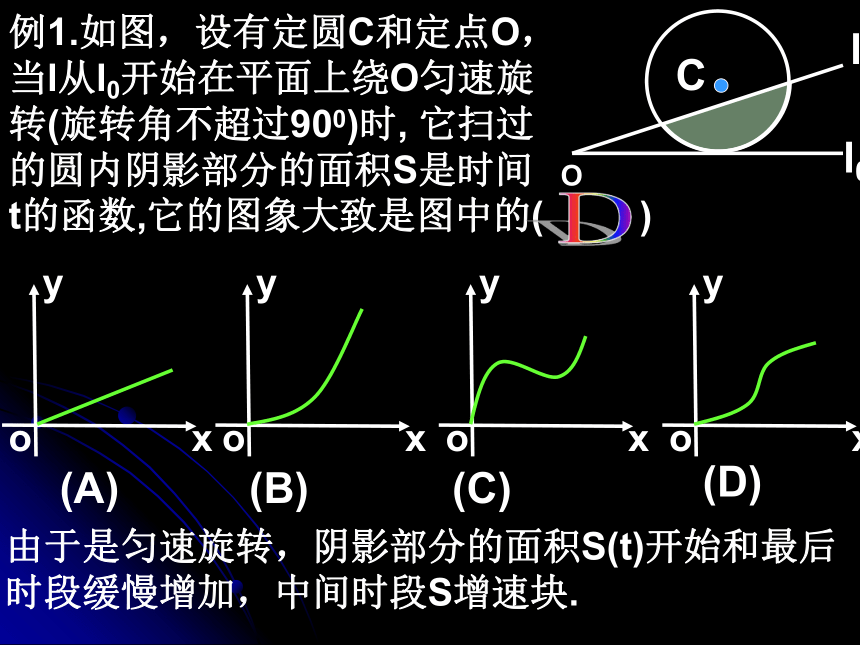
f ′ (x)=3x2≥0,其中f ′ (0)=0.例1.如图,设有定圆C和定点O,
当l从l0开始在平面上绕O匀速旋
转(旋转角不超过900)时, 它扫过
的圆内阴影部分的面积S是时间
t的函数,它的图象大致是图中的( )
(A)(B)(C)(D)D由于是匀速旋转,阴影部分的面积S(t)开始和最后
时段缓慢增加,中间时段S增速块.例2.对于函数y=x2-4x+3,你能用几种方法讨
论它在R上的单调性?定义法图象法f(x)在(-∞,2)
是减函数,
在(2,+∞)
是增函数.求导法解:y’=6x2-6x-12=6(x+1)(x-2)
令6x2-6x-12 ﹥0
解得x﹥2或x﹤-1
因此函数的增区间是:
(2,+?)和(- ? ,-1)
令6x2-6x-12 ﹤0
解得-1﹤x ﹤2
因此函数的减区间是:
(- 1 , 2)例3:求函数y=2x3-3x2-12x+14的递增区间和
递减区间.用导数研究函数的单调性比用定义法更为简便!图象2函数f(x)在x= -1和
x=2处改变增减性,
导数为0.-121-6小结:用导数判断函数单调性的法则:1.如果在(a,b)内,f ’(x)>0,则f(x)在此区间是增
函数,(a,b)为f(x)的单调增区间;2.如果在(a,b)内,f ’(x)<0,则f(x)在此区间是减
函数,(a,b)为f(x)的单调减区间;练习:选修1—1教材第26-27页,练习A练习B学习目标2.能应用求导方法判定函数的增减性及求出
函数的单调区间;领会学习导数的作用.1.掌握用求导数判断函数单调性的方法,并
会灵活应用;3.3.1利用导数判断函数的单调性(二)小测验 2.函数y =ex-x+1的递减区间是 .单调递减(-∞,0)递增区间 (1,+∞);递减区间 (-1,1)例1.若函数 y=x3+(p+1)x2+p2x+1在R上单调递增,求实数p的取值范围.例2.若函数f(x)=x3-ax2+1在(0,2)内单调递
减,则实数a的取值范围是 A . a ≥3 B . a =3
C . a ≤3 D . 0﹤a ﹤3A例3:已知函数y=x3-ax+6的一个单调递增区间是(1,+?).求a的值及函数其它的单调区间.∴1是方程y’=0的一个根.可求出a=3∴y’=3x2-3,由3x2-3 ﹥0,得x ﹥1或x ﹤-1,解:y’=3x2-a
∵函数的一个单调递增区间是(1,+?) ∴(- 1 ,1)是函数的一个递减区间.由3x2-3 ﹤ 0,得-1﹤ x ﹤1,∴(- ? ,-1)是函数的一个递增区间;小结:1.求函数的单调区间时不要忘记考虑函数的定义域;2.对于逆向思维的题目要注意已知条件给出的是函
数的一个单调区间?还是函数在一个区间上单调?若给出的是函数的一个单调区间,则函数在区间端
点处的导数为0;若给出的是函数在一个区间上单调,则这个区间应
是函数单调区间的一个子集.
函数的单调区间;领会学习导数的作用.1.掌握用求导数判断函数单调性的方法,并
会灵活应用;引例垂直上抛一个小沙袋,沙袋高度
h是时间t的函数,设为h=h(t),
其图象如图所示.横坐标轴表示时间,纵坐标轴表
示沙袋的高度,设沙袋的最高点
为A,其横坐标为t=t0.先考察沙袋在区间(a,t0)的运动情况:在区间(a,t0)内沙袋向上运动,其垂直向上的瞬时速
度大于0.即在(a,t0), 在此区间
内,函数h=h(t)是增函数.(t0,b)下小(t0,b)h’(t)<0减函数用导数判断函数单调性的法则:1.如果在(a,b)内,f ’(x)>0,则f(x)在此区间是增
函数,(a,b)为f(x)的单调增区间;2.如果在(a,b)内,f ’(x)<0,则f(x)在此区间是减
函数,(a,b)为f(x)的单调减区间;用函数曲线的切线的斜率来理解这个法则:当切线斜率为正时,切线的
倾斜角小于900, 函数曲线
呈上升状态;当切线斜率为
负时,函数曲线呈下降状态.对法则的理解:该法则只说明f ′ (x)>0(或 <0)是函数f(x)为增
(减)函数的充分条件但并不是必要的.例如,函数y=x3在实数集内是增函数,但有
f ′ (x)=3x2≥0,其中f ′ (0)=0.例1.如图,设有定圆C和定点O,
当l从l0开始在平面上绕O匀速旋
转(旋转角不超过900)时, 它扫过
的圆内阴影部分的面积S是时间
t的函数,它的图象大致是图中的( )
(A)(B)(C)(D)D由于是匀速旋转,阴影部分的面积S(t)开始和最后
时段缓慢增加,中间时段S增速块.例2.对于函数y=x2-4x+3,你能用几种方法讨
论它在R上的单调性?定义法图象法f(x)在(-∞,2)
是减函数,
在(2,+∞)
是增函数.求导法解:y’=6x2-6x-12=6(x+1)(x-2)
令6x2-6x-12 ﹥0
解得x﹥2或x﹤-1
因此函数的增区间是:
(2,+?)和(- ? ,-1)
令6x2-6x-12 ﹤0
解得-1﹤x ﹤2
因此函数的减区间是:
(- 1 , 2)例3:求函数y=2x3-3x2-12x+14的递增区间和
递减区间.用导数研究函数的单调性比用定义法更为简便!图象2函数f(x)在x= -1和
x=2处改变增减性,
导数为0.-121-6小结:用导数判断函数单调性的法则:1.如果在(a,b)内,f ’(x)>0,则f(x)在此区间是增
函数,(a,b)为f(x)的单调增区间;2.如果在(a,b)内,f ’(x)<0,则f(x)在此区间是减
函数,(a,b)为f(x)的单调减区间;练习:选修1—1教材第26-27页,练习A练习B学习目标2.能应用求导方法判定函数的增减性及求出
函数的单调区间;领会学习导数的作用.1.掌握用求导数判断函数单调性的方法,并
会灵活应用;3.3.1利用导数判断函数的单调性(二)小测验 2.函数y =ex-x+1的递减区间是 .单调递减(-∞,0)递增区间 (1,+∞);递减区间 (-1,1)例1.若函数 y=x3+(p+1)x2+p2x+1在R上单调递增,求实数p的取值范围.例2.若函数f(x)=x3-ax2+1在(0,2)内单调递
减,则实数a的取值范围是 A . a ≥3 B . a =3
C . a ≤3 D . 0﹤a ﹤3A例3:已知函数y=x3-ax+6的一个单调递增区间是(1,+?).求a的值及函数其它的单调区间.∴1是方程y’=0的一个根.可求出a=3∴y’=3x2-3,由3x2-3 ﹥0,得x ﹥1或x ﹤-1,解:y’=3x2-a
∵函数的一个单调递增区间是(1,+?) ∴(- 1 ,1)是函数的一个递减区间.由3x2-3 ﹤ 0,得-1﹤ x ﹤1,∴(- ? ,-1)是函数的一个递增区间;小结:1.求函数的单调区间时不要忘记考虑函数的定义域;2.对于逆向思维的题目要注意已知条件给出的是函
数的一个单调区间?还是函数在一个区间上单调?若给出的是函数的一个单调区间,则函数在区间端
点处的导数为0;若给出的是函数在一个区间上单调,则这个区间应
是函数单调区间的一个子集.
