正比例反比例学案(山东省东营市东营区)
文档属性
| 名称 | 正比例反比例学案(山东省东营市东营区) |

|
|
| 格式 | rar | ||
| 文件大小 | 354.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-02-27 00:00:00 | ||
图片预览


文档简介
课题:正比例、反比例(2)
设计人:古宝针 学校:东营区史口镇中学 使用人:
【学习目标】:
1.进一步理解正比例.反比例的意义,弄清它们的联系和区别,掌握它们的变化规律。
2.能正确判断正、反比例,提高分析、比较、抽象、概括能力,培养学习兴趣。
3.通过数“形”结合,进一步感受和领会正、反比例关系的变化规律及特点,进一步渗透函数思想,为今后中学的学习打下基础。
【重点、难点】
重点:正比例、反比例的意义,联系和区别。
难点::理解正、反比例关系的变化规律。
【学习过程】
一、知识回顾
1.两种相关联的量,一种量变化,另一种量也随着 。如果这两种量中相对应的两个数的 一定,这两种量就叫做成正比例的量,它们之间的关系叫做 关系。
2、两种相关联的量,一种量变化,另一种量也随着 。如果这两种量中相对应的两个数的 一定,这两种量就叫做成反比例的量,它们之间的关系叫做 关系。
你能举出生活中成正比例、反比例的例子吗?
二.探究新知:
1.判断下面每题中的两个量是否成正比例或反比例:
(1)出油率一定,香油质量与芝麻的质量。
(2)一捆100米长的电线,用去的长度与剩下的长度。
(3)三角形的面积一定,它的底和高。
(4)一个数与它的倒数。
2.
想一想:正、反比例中,它们的量都有哪些关系 有哪些相同点和不同点?
将它们的相同点和不同点填在表格中。
正比例 反比例
相同点
不同点
3.练一练:
(1)判断
①、工作总量一定,工作效率和工作时间成反比例。( )
②、图上距离和实际距离成正比例。( )
③、X和Y表示两种变化的相关联的量,同时5X-7Y=0,X和Y不成比例。( )
④、分数的大小一定,它的分子和分母成正比例。 ( )
⑤、在一定的距离内,车轮周长和它转动的圈数成反比例。 ( )
(2)在圆柱的侧面积、底面周长、高这三种量中
当底面周长一定时,( )与( )成( )比例;
当高一定时,( )与( )成( )比例;
当侧面积一定时,( )与( )成( )比例。
4.例题探究:
例1、磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 1 2 3 4 5 6 7 ……
路程/千米 7 14 21 28 35 42 49 ……
(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。
(2)连接各点,它们在一条直线上吗?
(3)根据图像判断,列车运行2分半钟时,行驶的路程是多少千米?行驶30千米大约需要几分钟?
分析:根据提供的各组数据描出图像的许多个点,再依次连成直线。路程和时间相对应的数的比值都是 ,即 一定,路程和时间成 ,图像是一条直线。对照图像,可以根据时间的值估计出路程的值,也可以根据路程的值估计出时间的值,估计时允许有一定的出入。
例2、下表是王师傅加工一批零件时,每小时加工零件个数随时间变化的情况。这两种量有什么关系?
.
每小时加工零件的个数/个 20 30 40 60 80 ……
加工的时间/时 12 8 6 4 3 ……
.
分析:(1)从上表可以看出,表中有 和 两种量。
(2)从左往右看,每小时加工零件的个数扩大,加工的时间反而 ;从右往左看,每小时加工零件的个数缩小,加工的时间反而 。所以它们是两种相关联的量。
(3)每小时加工零件的个数和相对应的加工的时间的 都始终不变
所以每小时加工零件的个数和加工的时间成 关系。
三、学以致用:
1、判断单价、数量和总价中一种量一定时,另外两种量成什么比例关系?为什么?
(1)单价一定,数量和总价 ( )
(2)总价一定,数量和单价 ( )
(3)数量一定,总价和单价 ( )
2、从长方形的长、宽和面积三种量中,你能找出几种比例关系?
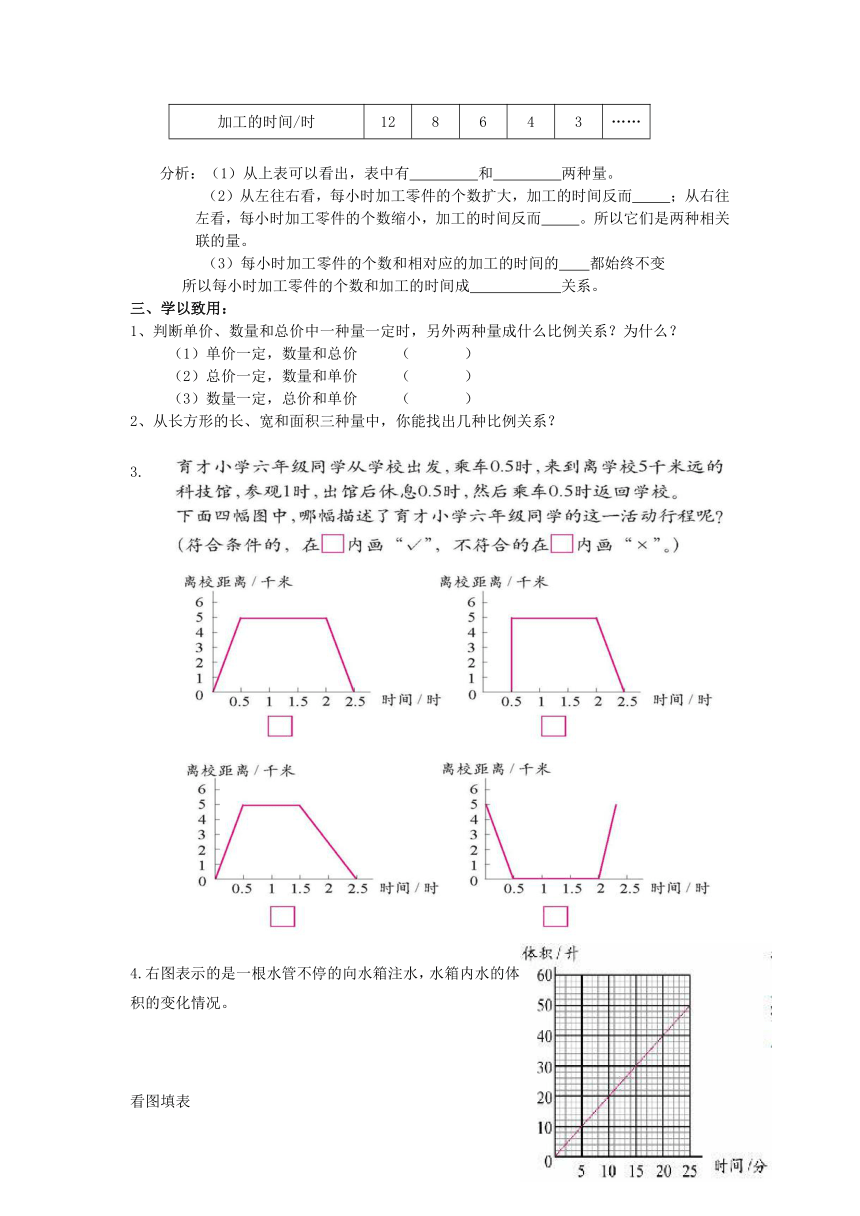
3.
4.右图表示的是一根水管不停的向水箱注水,水箱内水的体积的变化情况。
看图填表
注水时间/分 5 8 13
水的体积/升 10 20 46
思考:图中哪些量是发生变化的?哪些量是不变的?变化的量之间是怎样的关系?你是如何发现的?
四、知识小结:
1.通过本节课的学习和交流,你有哪些收获?和你的同桌说一说。
2.关于正比例和反比例,你还有哪些问题?请会的同学帮助解答。
3.你还想了解有关正、反比例的哪些知识?老师可以给你们做一点简单的介绍。
五、布置作业:
举出正比例、反比例的一些例子,并试着分别描点作图,观察比较,把自己的发现在小组内交流。
六、诊断检测(一)
1.根据表格填空。
表中两种相关联的量是( )和( ),这两种量中相对应的两个数的( ),即( )一定,所以( )和( )成( )比例。
2、判断下面每题中的两种量是不是成比例,如果成比例,成什么比例。
(1)、装配一批电视机,每天装配台数和所需的天数( )。
(2)、正方形的边长和周长( )。
(3)、水池的容积一定,水管每小时注水量和所用时间( )。
(4)、房间面积一定,每块砖的面积和铺砖的块数( )。
(5)、在一定时间里,加工每个零件所用的时间和加工零件的个数( )。
3、某造纸厂每小时造纸1.5吨,2小时、3小时┈┈各造纸多少吨?
(1)把下表填写完整。
.
造纸时间/时 1 2 3 4 ……
造纸吨数/吨 1.5 ……
(2)根据表中的数据,在下图中描出造纸时间和造纸吨数对应的点,再把它们连起来。
(3)造纸吨数与造纸时间成正比例吗?为什么?
(4)根据图像判断, 5小时造纸多少吨?
诊断检测(一)答案:
1.大米的袋数 大米的重量 比值 商 大米的袋数 大米的重量 正.
2. (1)反比例;(2)正比例;(3)反比例;(4)反比例;(5)反比例;
3. (1)把下表填写完整。
.造纸时间/时 1 2 3 4 ……
造纸吨数/吨 1.5 3 4.5 6 ……
(2)
(3)因为造纸吨数/造纸时间= 每小时造纸吨数(一定),所以每小时造纸吨数一定时,造纸吨数与造纸时间成正比例。
(4)根据图像判断,5小时造纸7.5吨。
诊断检测(二)
1、.判断:
(1)订阅《小学数学评价手册》的份数与所需钱数成正比例。 ( )
(2)在400米赛跑中,跑步的速度和所用时间成反比例。 ( )
(3)工作总量一定,已完成的量和未完成的量成反比例。 ( )
(4)正方体的棱长和体积成正比例。 ( )
(5)被除数一定,除数和商成反比例。 ( )
(6)圆的周长和它的直径成正比例。
2.先判断下表中两种量成什么比例,然后填表。
表中x和y成( ) 比例.
表中x和y成( ) 比例.
3、分别说明大米的总千克数、每天吃的千克数和天数这三种量中,每两种量的比例关系。
(1)大米的总千克数一定,每天吃的千克数和天数;
(2)每天吃的千克数一定,大米的总千克数和天数;
(3)天数一定,大米的总千克数和每天吃的千克数。
4、明明三岁时体重12千克,十一岁时体重44千克。于是小张就说:“明明的体重和身高成正比例。”你认为小张的说法对吗?为什么?
诊断检测(二)答案:
1. (1)√;(2)√;(3)×;(4)×;(5)√;(6)√。
2. (1)正(表略) (2)反(表略)
3.(1)、成反比例(2)、成正比例(3)成正比例
4. 小张的说法是错误的,体重和身高不是两种相关联的量,体重和身高不成比例。
设计人:古宝针 学校:东营区史口镇中学 使用人:
【学习目标】:
1.进一步理解正比例.反比例的意义,弄清它们的联系和区别,掌握它们的变化规律。
2.能正确判断正、反比例,提高分析、比较、抽象、概括能力,培养学习兴趣。
3.通过数“形”结合,进一步感受和领会正、反比例关系的变化规律及特点,进一步渗透函数思想,为今后中学的学习打下基础。
【重点、难点】
重点:正比例、反比例的意义,联系和区别。
难点::理解正、反比例关系的变化规律。
【学习过程】
一、知识回顾
1.两种相关联的量,一种量变化,另一种量也随着 。如果这两种量中相对应的两个数的 一定,这两种量就叫做成正比例的量,它们之间的关系叫做 关系。
2、两种相关联的量,一种量变化,另一种量也随着 。如果这两种量中相对应的两个数的 一定,这两种量就叫做成反比例的量,它们之间的关系叫做 关系。
你能举出生活中成正比例、反比例的例子吗?
二.探究新知:
1.判断下面每题中的两个量是否成正比例或反比例:
(1)出油率一定,香油质量与芝麻的质量。
(2)一捆100米长的电线,用去的长度与剩下的长度。
(3)三角形的面积一定,它的底和高。
(4)一个数与它的倒数。
2.
想一想:正、反比例中,它们的量都有哪些关系 有哪些相同点和不同点?
将它们的相同点和不同点填在表格中。
正比例 反比例
相同点
不同点
3.练一练:
(1)判断
①、工作总量一定,工作效率和工作时间成反比例。( )
②、图上距离和实际距离成正比例。( )
③、X和Y表示两种变化的相关联的量,同时5X-7Y=0,X和Y不成比例。( )
④、分数的大小一定,它的分子和分母成正比例。 ( )
⑤、在一定的距离内,车轮周长和它转动的圈数成反比例。 ( )
(2)在圆柱的侧面积、底面周长、高这三种量中
当底面周长一定时,( )与( )成( )比例;
当高一定时,( )与( )成( )比例;
当侧面积一定时,( )与( )成( )比例。
4.例题探究:
例1、磁悬浮列车匀速行驶时,路程与时间的关系如下。
时间/分 1 2 3 4 5 6 7 ……
路程/千米 7 14 21 28 35 42 49 ……
(1)图中的点A表示时间为1分钟时,磁悬浮列车驶过的路程为7千米。请你试着描出其他各点。
(2)连接各点,它们在一条直线上吗?
(3)根据图像判断,列车运行2分半钟时,行驶的路程是多少千米?行驶30千米大约需要几分钟?
分析:根据提供的各组数据描出图像的许多个点,再依次连成直线。路程和时间相对应的数的比值都是 ,即 一定,路程和时间成 ,图像是一条直线。对照图像,可以根据时间的值估计出路程的值,也可以根据路程的值估计出时间的值,估计时允许有一定的出入。
例2、下表是王师傅加工一批零件时,每小时加工零件个数随时间变化的情况。这两种量有什么关系?
.
每小时加工零件的个数/个 20 30 40 60 80 ……
加工的时间/时 12 8 6 4 3 ……
.
分析:(1)从上表可以看出,表中有 和 两种量。
(2)从左往右看,每小时加工零件的个数扩大,加工的时间反而 ;从右往左看,每小时加工零件的个数缩小,加工的时间反而 。所以它们是两种相关联的量。
(3)每小时加工零件的个数和相对应的加工的时间的 都始终不变
所以每小时加工零件的个数和加工的时间成 关系。
三、学以致用:
1、判断单价、数量和总价中一种量一定时,另外两种量成什么比例关系?为什么?
(1)单价一定,数量和总价 ( )
(2)总价一定,数量和单价 ( )
(3)数量一定,总价和单价 ( )
2、从长方形的长、宽和面积三种量中,你能找出几种比例关系?
3.
4.右图表示的是一根水管不停的向水箱注水,水箱内水的体积的变化情况。
看图填表
注水时间/分 5 8 13
水的体积/升 10 20 46
思考:图中哪些量是发生变化的?哪些量是不变的?变化的量之间是怎样的关系?你是如何发现的?
四、知识小结:
1.通过本节课的学习和交流,你有哪些收获?和你的同桌说一说。
2.关于正比例和反比例,你还有哪些问题?请会的同学帮助解答。
3.你还想了解有关正、反比例的哪些知识?老师可以给你们做一点简单的介绍。
五、布置作业:
举出正比例、反比例的一些例子,并试着分别描点作图,观察比较,把自己的发现在小组内交流。
六、诊断检测(一)
1.根据表格填空。
表中两种相关联的量是( )和( ),这两种量中相对应的两个数的( ),即( )一定,所以( )和( )成( )比例。
2、判断下面每题中的两种量是不是成比例,如果成比例,成什么比例。
(1)、装配一批电视机,每天装配台数和所需的天数( )。
(2)、正方形的边长和周长( )。
(3)、水池的容积一定,水管每小时注水量和所用时间( )。
(4)、房间面积一定,每块砖的面积和铺砖的块数( )。
(5)、在一定时间里,加工每个零件所用的时间和加工零件的个数( )。
3、某造纸厂每小时造纸1.5吨,2小时、3小时┈┈各造纸多少吨?
(1)把下表填写完整。
.
造纸时间/时 1 2 3 4 ……
造纸吨数/吨 1.5 ……
(2)根据表中的数据,在下图中描出造纸时间和造纸吨数对应的点,再把它们连起来。
(3)造纸吨数与造纸时间成正比例吗?为什么?
(4)根据图像判断, 5小时造纸多少吨?
诊断检测(一)答案:
1.大米的袋数 大米的重量 比值 商 大米的袋数 大米的重量 正.
2. (1)反比例;(2)正比例;(3)反比例;(4)反比例;(5)反比例;
3. (1)把下表填写完整。
.造纸时间/时 1 2 3 4 ……
造纸吨数/吨 1.5 3 4.5 6 ……
(2)
(3)因为造纸吨数/造纸时间= 每小时造纸吨数(一定),所以每小时造纸吨数一定时,造纸吨数与造纸时间成正比例。
(4)根据图像判断,5小时造纸7.5吨。
诊断检测(二)
1、.判断:
(1)订阅《小学数学评价手册》的份数与所需钱数成正比例。 ( )
(2)在400米赛跑中,跑步的速度和所用时间成反比例。 ( )
(3)工作总量一定,已完成的量和未完成的量成反比例。 ( )
(4)正方体的棱长和体积成正比例。 ( )
(5)被除数一定,除数和商成反比例。 ( )
(6)圆的周长和它的直径成正比例。
2.先判断下表中两种量成什么比例,然后填表。
表中x和y成( ) 比例.
表中x和y成( ) 比例.
3、分别说明大米的总千克数、每天吃的千克数和天数这三种量中,每两种量的比例关系。
(1)大米的总千克数一定,每天吃的千克数和天数;
(2)每天吃的千克数一定,大米的总千克数和天数;
(3)天数一定,大米的总千克数和每天吃的千克数。
4、明明三岁时体重12千克,十一岁时体重44千克。于是小张就说:“明明的体重和身高成正比例。”你认为小张的说法对吗?为什么?
诊断检测(二)答案:
1. (1)√;(2)√;(3)×;(4)×;(5)√;(6)√。
2. (1)正(表略) (2)反(表略)
3.(1)、成反比例(2)、成正比例(3)成正比例
4. 小张的说法是错误的,体重和身高不是两种相关联的量,体重和身高不成比例。
