西师大版2023-2024学年小学六年级上册数学寒假分类作业集训:与圆相关的综合解答题专练(附答案)
文档属性
| 名称 | 西师大版2023-2024学年小学六年级上册数学寒假分类作业集训:与圆相关的综合解答题专练(附答案) |  | |
| 格式 | docx | ||
| 文件大小 | 318.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 17:51:34 | ||
图片预览

文档简介
西师大版2023-2024学年小学六年级上册数学寒假分类
作业集训:与圆相关的综合解答题专练
1.下图ABCD是边长为10厘米的正方形,且AB是半圆的直径,求阴影部分的面积。
2.太极图在中国传统文化中含义深邃,其形状为阴阳两鱼互纠在一起,象征两极和合。下图中大圆的直径是10cm,阴鱼(即阴影部分)的面积是多少?
3.如图中阴影部分①和阴影部分②的面积相差多少cm2?(单位:cm)
4.下面是广场上地砖拼成的图案,已知AB=BC=CD=10米,阴影部分地砖的面积是多少平方米?
5.下图中正方形的面积是8平方厘米,阴影部分的面积是多少平方厘米?
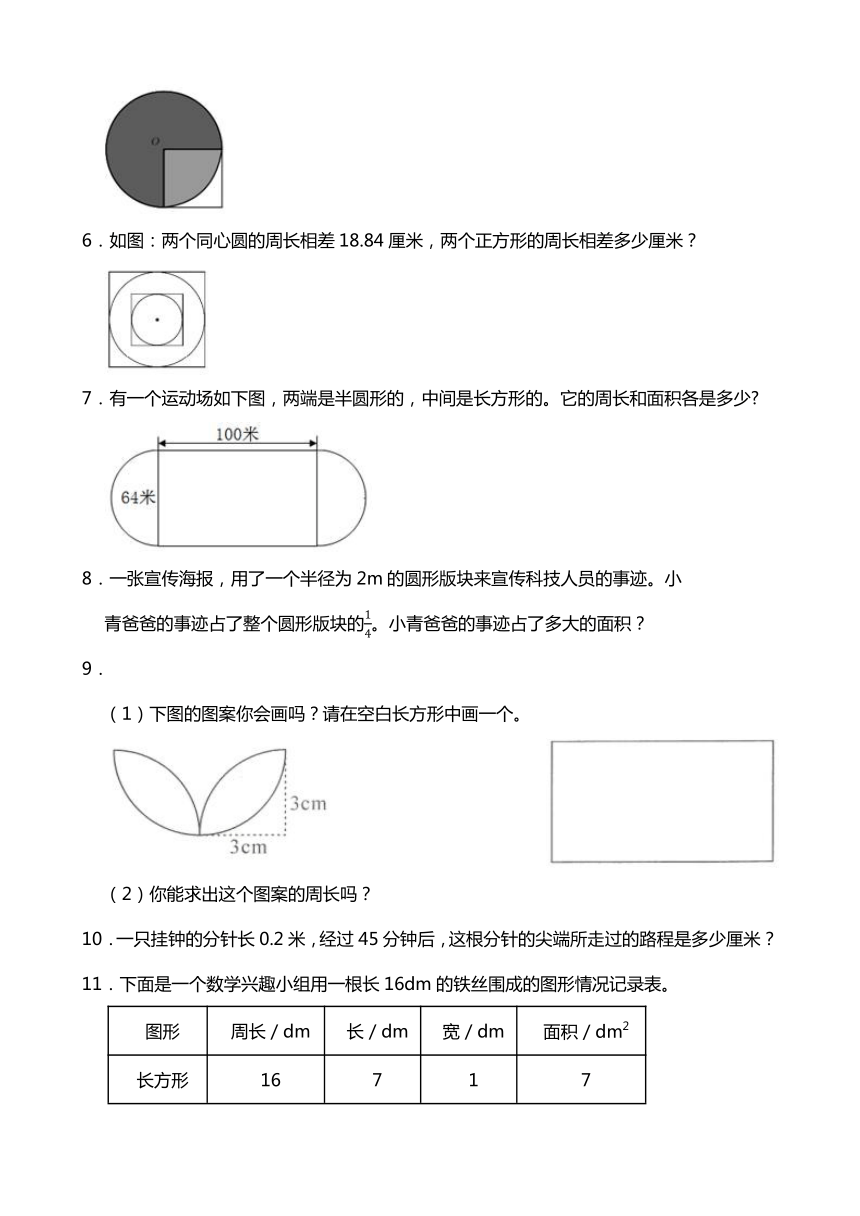
6.如图:两个同心圆的周长相差18.84厘米,两个正方形的周长相差多少厘米?
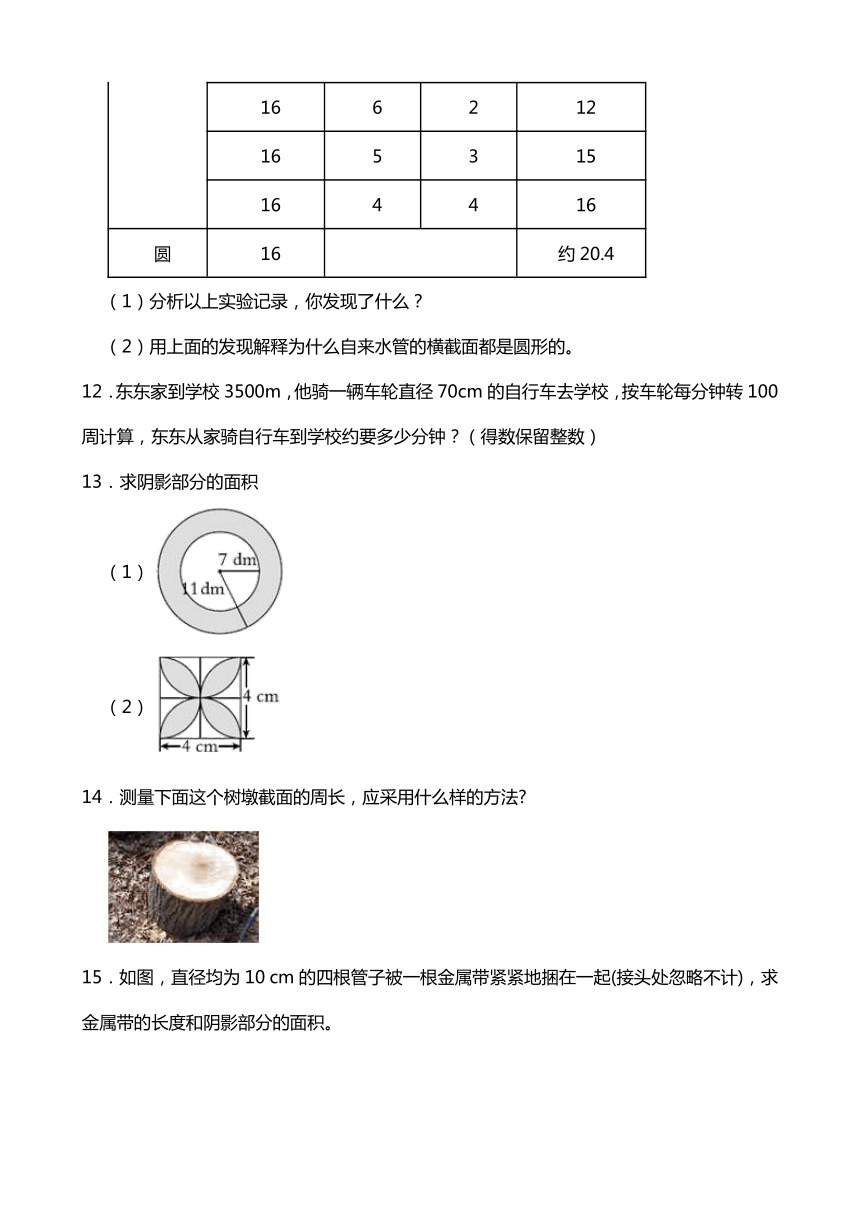
7.有一个运动场如下图,两端是半圆形的,中间是长方形的。它的周长和面积各是多少
8.一张宣传海报,用了一个半径为2m的圆形版块来宣传科技人员的事迹。小
青爸爸的事迹占了整个圆形版块的。小青爸爸的事迹占了多大的面积?
9.
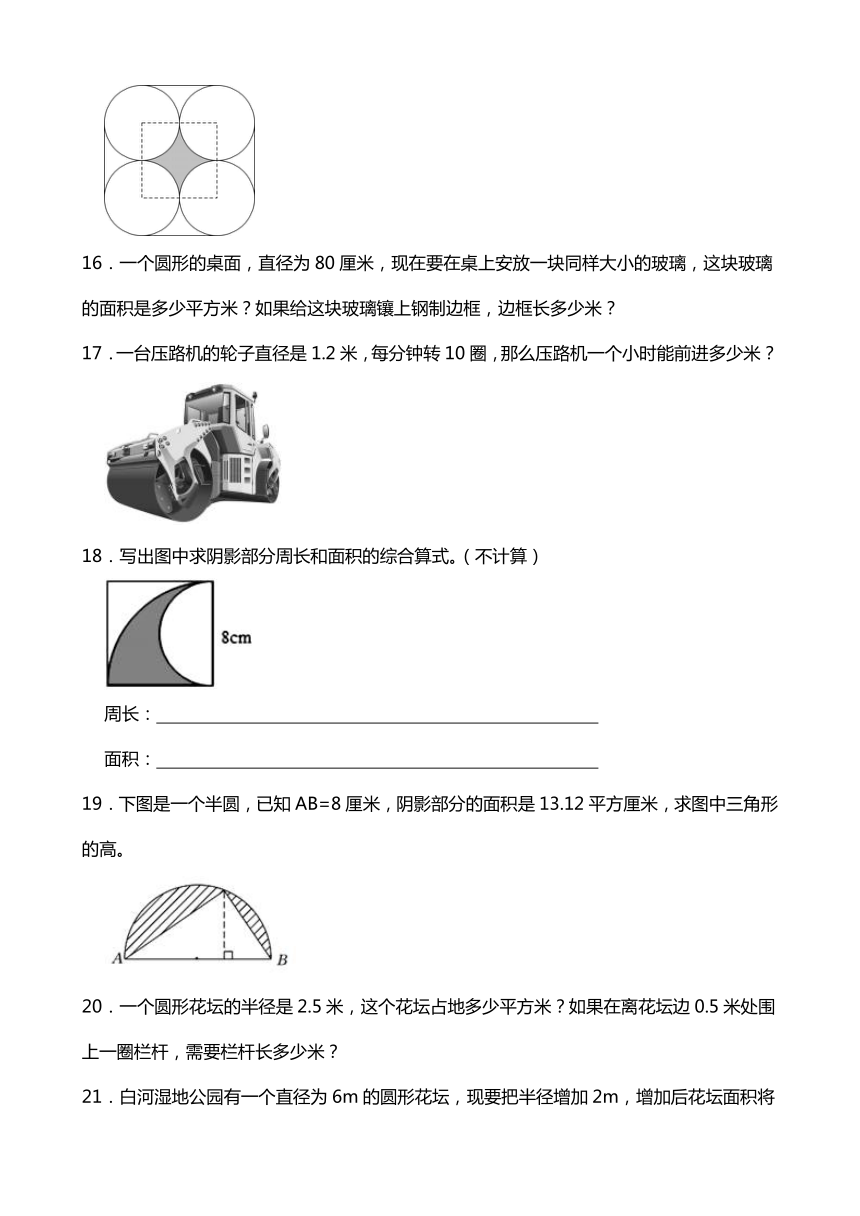
(1)下图的图案你会画吗?请在空白长方形中画一个。
(2)你能求出这个图案的周长吗?
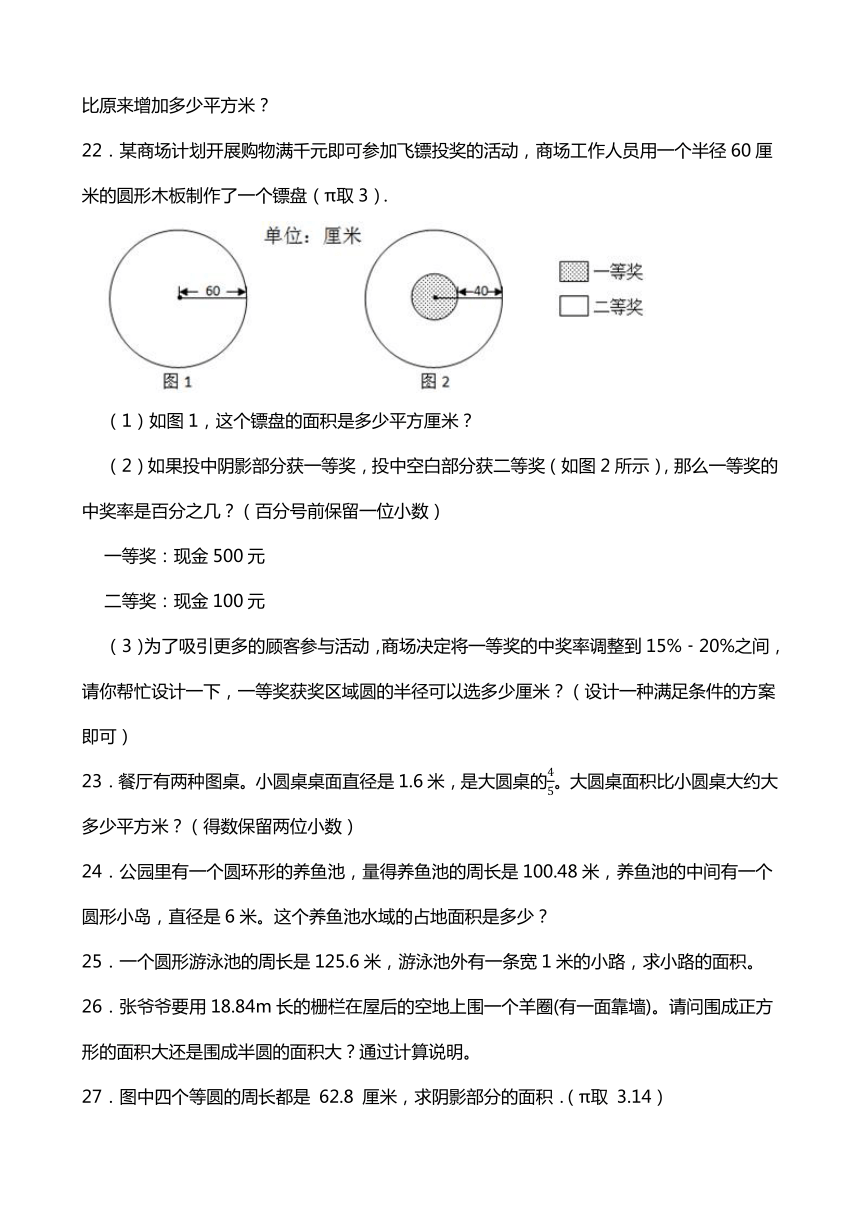
10.一只挂钟的分针长0.2米,经过45分钟后,这根分针的尖端所走过的路程是多少厘米?
11.下面是一个数学兴趣小组用一根长16dm的铁丝围成的图形情况记录表。
图形 周长/dm 长/dm 宽/dm 面积/dm2
长方形 16 7 1 7
16 6 2 12
16 5 3 15
16 4 4 16
圆 16 约20.4
(1)分析以上实验记录,你发现了什么?
(2)用上面的发现解释为什么自来水管的横截面都是圆形的。
12.东东家到学校3500m,他骑一辆车轮直径70cm的自行车去学校,按车轮每分钟转100周计算,东东从家骑自行车到学校约要多少分钟?(得数保留整数)
13.求阴影部分的面积
(1)
(2)
14.测量下面这个树墩截面的周长,应采用什么样的方法
15.如图,直径均为10 cm的四根管子被一根金属带紧紧地捆在一起(接头处忽略不计),求金属带的长度和阴影部分的面积。
16.一个圆形的桌面,直径为80厘米,现在要在桌上安放一块同样大小的玻璃,这块玻璃的面积是多少平方米?如果给这块玻璃镶上钢制边框,边框长多少米?
17.一台压路机的轮子直径是1.2米,每分钟转10圈,那么压路机一个小时能前进多少米?
18.写出图中求阴影部分周长和面积的综合算式。(不计算)
周长:
面积:
19.下图是一个半圆,已知AB=8厘米,阴影部分的面积是13.12平方厘米,求图中三角形的高。
20.一个圆形花坛的半径是2.5米,这个花坛占地多少平方米?如果在离花坛边0.5米处围上一圈栏杆,需要栏杆长多少米?
21.白河湿地公园有一个直径为6m的圆形花坛,现要把半径增加2m,增加后花坛面积将比原来增加多少平方米?
22.某商场计划开展购物满千元即可参加飞镖投奖的活动,商场工作人员用一个半径60厘米的圆形木板制作了一个镖盘(π取3).
(1)如图1,这个镖盘的面积是多少平方厘米?
(2)如果投中阴影部分获一等奖,投中空白部分获二等奖(如图2所示),那么一等奖的中奖率是百分之几?(百分号前保留一位小数)
一等奖:现金500元
二等奖:现金100元
(3)为了吸引更多的顾客参与活动,商场决定将一等奖的中奖率调整到15%﹣20%之间,请你帮忙设计一下,一等奖获奖区域圆的半径可以选多少厘米?(设计一种满足条件的方案即可)
23.餐厅有两种图桌。小圆桌桌面直径是1.6米,是大圆桌的。大圆桌面积比小圆桌大约大多少平方米?(得数保留两位小数)
24.公园里有一个圆环形的养鱼池,量得养鱼池的周长是100.48米,养鱼池的中间有一个圆形小岛,直径是6米。这个养鱼池水域的占地面积是多少?
25.一个圆形游泳池的周长是125.6米,游泳池外有一条宽1米的小路,求小路的面积。
26.张爷爷要用18.84m长的栅栏在屋后的空地上围一个羊圈(有一面靠墙)。请问围成正方形的面积大还是围成半圆的面积大?通过计算说明。
27.图中四个等圆的周长都是 62.8 厘米,求阴影部分的面积.(π取 3.14)
28.认真观察下图,求出图1的周长,图2阴影部分的面积。
(1)
(2)
29.如图是由两个正方形和一个圆组成的,已知大正方形的面积是36cm2,那么阴影部分的面积是多少?(圆周率π取3.14)
答案
1.解:连接BD交AC于点O,且点O在半圆上,如图
可得图中绿色部分的面积=半圆中阴影部分的面积,
所以阴影部分的面积=△BOC的面积=×(10×10)
=×100
=25(平方厘米)
所以阴影部分的面积是25平方厘米。
2.解:10÷2=5(厘米)
3.14×52÷2
=3.14×25÷2
=78.5÷2
=39.25(平方厘米)
答:阴鱼(即阴影部分)的面积是39.25平方厘米。
3.解:
②+③+④=3.14×5×5÷4=19.625(平方厘米)
①+③+④=(5-2)×5+3.14×2×2÷4=15+3.14=18.14(平方厘米)
19.625-18.14=1.485(平方厘米)
答:阴影部分①和阴影部分②的面积相差1.485平方厘米。
4.解:10÷2=5(米)
3.14×102-3.14×52
=3.14×100-3.14×25
=314-78.5
=235.5(平方米)
答:阴影部分地砖的面积是235.5平方米。
5.解:3.14×8×
=25.12×
=18.84(平方厘米)
答:涂色部分的面积是18.84平方厘米。
6.解:由分析可得:
18.84÷3.14×4
=6×4
=24(厘米)
答:两个正方形的周长相差24厘米。
7.解:64×3.14+100×2=400.96(米)
(64÷2)2×3.14+100×64=9615.36(平方米)
答:它的周长是400.96米,面积是9615.36平方米。
8.解:3.14×22×
=12.56×
=3.14(平方米)
答:小青爸爸的事迹占了3.14平方米。
9.(1)
(2)解:由4个 半径为3cm的圆弧组成:4× ×π·d=3.14×6=18.84(cm)
10.解:3.14×(0.2×2)×(45÷60)
=3.14×0.4×0.75
=1.256×0.75
=0.942(米)
0.942米=94.2厘米
答:这根分针的尖端所走过的路程是94.2厘米。
11.(1)解:发现:周长相等的长方形、正方形和圆中,圆的面积最大。
(2)解:所用材料相同的情况下,横截面是圆形,面积最大,供水最快、最好。
12.解:3500米=350000厘米
350000÷(70×3.14×100)
=350000÷23800
≈16(分钟)
答:东东从家骑自行车到学校约要16分钟。
13.(1)解:3.14×(112-72)
=3.14×(121-49)
=3.14×72
=226.08(dm2)
(2)解:4÷2=2(cm)
4×4-(2×2-3.14×22÷4)×8
=16-(4-3.14)×8
=16-0.86×8
=16-6.88
=9.12(cm2)
14.解:可采用软尺或线绳测量
15.解:10×4+3.14×10
=40+31.4
=71.4(厘米)
10÷2=5(厘米)
10×10-3.14×52
=100-78.5
=21.5(平方厘米)
答:金属带的长度是71.4厘米;阴影部分的面积是21.5平方厘米。
16.解:80÷2=40(厘米)=0.4(米)
面积:3.14×0.42=0.5024(平方米)
周长:3.14×0.8=2.512(米)
答:这块玻璃的面积是0.5024平方米,边框长2.512米。
17.解:3.14×1.2×10×60
=3.768×10×60
=37.68×60
=2260.8(米)
答:压路机一个小时能前进2260.8米。
18.解:周长:3.14×8÷2+3.14×8×2× +8
面积:3.14×82× ﹣3.14×(8÷2)2÷2
19.解:8÷2=4(厘米)
3.14×42× =25.12(平方厘米)
25.12-13.12=12(平方厘米)
12×2÷8=3(厘米)
答:三角形的高是3厘米。
20.解:3.14×2.52=19.625(平方米)
2.5+0.5=3(米)
3.14×3×2
=3.14×6
=18.84(米)
答:这个花坛占地19.625平方米,需要栏杆长18.84米。
21.解:6÷2=3(米)
3+2=5(米)
3.14×(52-32)
=3.14×(25-9)
=3.14×16
=50.24(平方米)
答:增加后花坛面积将比原来增加50.24平方米。
22.(1)解:3×60×60=10800(平方厘米)
答:这个镖盘的面积是10800平方厘米。
(2)解:60﹣40=20(厘米)
3×20×20÷10800≈11.1%
答:一等奖的中奖率是11.1%。
(3)解:将一等奖的中奖率调整到16%,
3×60×60×16%÷3
=36×16
=6×6×4×4
=(6×4)×(6×4)
=24×24
答:所以一等奖获奖区域圆的半径可以选24厘米。
23.解:1.6÷=2(米)
3.14×[(2÷2)2﹣(1.6÷2)2]
=3.14×[1﹣0.64]
=3.14×0.36
=1.1304
≈1.13(平方米)
答:大圆桌面积比小圆桌大约大1.13平方米。
24.解:100.48÷3.14÷2
=32÷2
=16(米)
6÷2=3(米)
3.14×(162-32)
=3.14×(256-9)
=3.14×247
=775.58(平方米)
答:这个养鱼池水域的占地面积是775.58平方米。
25.解:125.6÷3.14÷2
=40÷2
=20(米)
20+1=21(米)
3.14×(212-202)
=3.14×(441-400)
=3.14×41
=128.74(平方米)
答:小路的面积是128.74平方米。
26.解:正方形边长:18.84÷3=6.28(米)
正方形面积:6.28×6.28=39.4384(平方米)
半圆的半径:18.84×2÷3.14÷2=6(米)
半圆的面积:3.14×62÷2=56.52(平方米)
56.52>39.4384
答:围成半圆的面积大。
27.解:阴影部分圆心角为四边形内角和,即360度,所以阴影部分组合起来为一个圆,
半径:62.8÷3.14÷2=10(厘米)
阴影部分面积:10×10×3.14=314(平方厘米)
答:阴影部分的面积为314平方厘米。
28.(1)解:2+1×2+3.14×2÷2
=2+2+3.14
=7.14(cm)
(2)解:4×4-3.14×(4÷2)2
=16-3.14×4
=16-12.56
=3.44(cm2)
29.解:阴影部分的面积=×36-36÷2
=9×3.14-18
=28.26-18
=10.26(cm2)
答:阴影部分的面积是10.26cm2。
作业集训:与圆相关的综合解答题专练
1.下图ABCD是边长为10厘米的正方形,且AB是半圆的直径,求阴影部分的面积。
2.太极图在中国传统文化中含义深邃,其形状为阴阳两鱼互纠在一起,象征两极和合。下图中大圆的直径是10cm,阴鱼(即阴影部分)的面积是多少?
3.如图中阴影部分①和阴影部分②的面积相差多少cm2?(单位:cm)
4.下面是广场上地砖拼成的图案,已知AB=BC=CD=10米,阴影部分地砖的面积是多少平方米?
5.下图中正方形的面积是8平方厘米,阴影部分的面积是多少平方厘米?
6.如图:两个同心圆的周长相差18.84厘米,两个正方形的周长相差多少厘米?
7.有一个运动场如下图,两端是半圆形的,中间是长方形的。它的周长和面积各是多少
8.一张宣传海报,用了一个半径为2m的圆形版块来宣传科技人员的事迹。小
青爸爸的事迹占了整个圆形版块的。小青爸爸的事迹占了多大的面积?
9.
(1)下图的图案你会画吗?请在空白长方形中画一个。
(2)你能求出这个图案的周长吗?
10.一只挂钟的分针长0.2米,经过45分钟后,这根分针的尖端所走过的路程是多少厘米?
11.下面是一个数学兴趣小组用一根长16dm的铁丝围成的图形情况记录表。
图形 周长/dm 长/dm 宽/dm 面积/dm2
长方形 16 7 1 7
16 6 2 12
16 5 3 15
16 4 4 16
圆 16 约20.4
(1)分析以上实验记录,你发现了什么?
(2)用上面的发现解释为什么自来水管的横截面都是圆形的。
12.东东家到学校3500m,他骑一辆车轮直径70cm的自行车去学校,按车轮每分钟转100周计算,东东从家骑自行车到学校约要多少分钟?(得数保留整数)
13.求阴影部分的面积
(1)
(2)
14.测量下面这个树墩截面的周长,应采用什么样的方法
15.如图,直径均为10 cm的四根管子被一根金属带紧紧地捆在一起(接头处忽略不计),求金属带的长度和阴影部分的面积。
16.一个圆形的桌面,直径为80厘米,现在要在桌上安放一块同样大小的玻璃,这块玻璃的面积是多少平方米?如果给这块玻璃镶上钢制边框,边框长多少米?
17.一台压路机的轮子直径是1.2米,每分钟转10圈,那么压路机一个小时能前进多少米?
18.写出图中求阴影部分周长和面积的综合算式。(不计算)
周长:
面积:
19.下图是一个半圆,已知AB=8厘米,阴影部分的面积是13.12平方厘米,求图中三角形的高。
20.一个圆形花坛的半径是2.5米,这个花坛占地多少平方米?如果在离花坛边0.5米处围上一圈栏杆,需要栏杆长多少米?
21.白河湿地公园有一个直径为6m的圆形花坛,现要把半径增加2m,增加后花坛面积将比原来增加多少平方米?
22.某商场计划开展购物满千元即可参加飞镖投奖的活动,商场工作人员用一个半径60厘米的圆形木板制作了一个镖盘(π取3).
(1)如图1,这个镖盘的面积是多少平方厘米?
(2)如果投中阴影部分获一等奖,投中空白部分获二等奖(如图2所示),那么一等奖的中奖率是百分之几?(百分号前保留一位小数)
一等奖:现金500元
二等奖:现金100元
(3)为了吸引更多的顾客参与活动,商场决定将一等奖的中奖率调整到15%﹣20%之间,请你帮忙设计一下,一等奖获奖区域圆的半径可以选多少厘米?(设计一种满足条件的方案即可)
23.餐厅有两种图桌。小圆桌桌面直径是1.6米,是大圆桌的。大圆桌面积比小圆桌大约大多少平方米?(得数保留两位小数)
24.公园里有一个圆环形的养鱼池,量得养鱼池的周长是100.48米,养鱼池的中间有一个圆形小岛,直径是6米。这个养鱼池水域的占地面积是多少?
25.一个圆形游泳池的周长是125.6米,游泳池外有一条宽1米的小路,求小路的面积。
26.张爷爷要用18.84m长的栅栏在屋后的空地上围一个羊圈(有一面靠墙)。请问围成正方形的面积大还是围成半圆的面积大?通过计算说明。
27.图中四个等圆的周长都是 62.8 厘米,求阴影部分的面积.(π取 3.14)
28.认真观察下图,求出图1的周长,图2阴影部分的面积。
(1)
(2)
29.如图是由两个正方形和一个圆组成的,已知大正方形的面积是36cm2,那么阴影部分的面积是多少?(圆周率π取3.14)
答案
1.解:连接BD交AC于点O,且点O在半圆上,如图
可得图中绿色部分的面积=半圆中阴影部分的面积,
所以阴影部分的面积=△BOC的面积=×(10×10)
=×100
=25(平方厘米)
所以阴影部分的面积是25平方厘米。
2.解:10÷2=5(厘米)
3.14×52÷2
=3.14×25÷2
=78.5÷2
=39.25(平方厘米)
答:阴鱼(即阴影部分)的面积是39.25平方厘米。
3.解:
②+③+④=3.14×5×5÷4=19.625(平方厘米)
①+③+④=(5-2)×5+3.14×2×2÷4=15+3.14=18.14(平方厘米)
19.625-18.14=1.485(平方厘米)
答:阴影部分①和阴影部分②的面积相差1.485平方厘米。
4.解:10÷2=5(米)
3.14×102-3.14×52
=3.14×100-3.14×25
=314-78.5
=235.5(平方米)
答:阴影部分地砖的面积是235.5平方米。
5.解:3.14×8×
=25.12×
=18.84(平方厘米)
答:涂色部分的面积是18.84平方厘米。
6.解:由分析可得:
18.84÷3.14×4
=6×4
=24(厘米)
答:两个正方形的周长相差24厘米。
7.解:64×3.14+100×2=400.96(米)
(64÷2)2×3.14+100×64=9615.36(平方米)
答:它的周长是400.96米,面积是9615.36平方米。
8.解:3.14×22×
=12.56×
=3.14(平方米)
答:小青爸爸的事迹占了3.14平方米。
9.(1)
(2)解:由4个 半径为3cm的圆弧组成:4× ×π·d=3.14×6=18.84(cm)
10.解:3.14×(0.2×2)×(45÷60)
=3.14×0.4×0.75
=1.256×0.75
=0.942(米)
0.942米=94.2厘米
答:这根分针的尖端所走过的路程是94.2厘米。
11.(1)解:发现:周长相等的长方形、正方形和圆中,圆的面积最大。
(2)解:所用材料相同的情况下,横截面是圆形,面积最大,供水最快、最好。
12.解:3500米=350000厘米
350000÷(70×3.14×100)
=350000÷23800
≈16(分钟)
答:东东从家骑自行车到学校约要16分钟。
13.(1)解:3.14×(112-72)
=3.14×(121-49)
=3.14×72
=226.08(dm2)
(2)解:4÷2=2(cm)
4×4-(2×2-3.14×22÷4)×8
=16-(4-3.14)×8
=16-0.86×8
=16-6.88
=9.12(cm2)
14.解:可采用软尺或线绳测量
15.解:10×4+3.14×10
=40+31.4
=71.4(厘米)
10÷2=5(厘米)
10×10-3.14×52
=100-78.5
=21.5(平方厘米)
答:金属带的长度是71.4厘米;阴影部分的面积是21.5平方厘米。
16.解:80÷2=40(厘米)=0.4(米)
面积:3.14×0.42=0.5024(平方米)
周长:3.14×0.8=2.512(米)
答:这块玻璃的面积是0.5024平方米,边框长2.512米。
17.解:3.14×1.2×10×60
=3.768×10×60
=37.68×60
=2260.8(米)
答:压路机一个小时能前进2260.8米。
18.解:周长:3.14×8÷2+3.14×8×2× +8
面积:3.14×82× ﹣3.14×(8÷2)2÷2
19.解:8÷2=4(厘米)
3.14×42× =25.12(平方厘米)
25.12-13.12=12(平方厘米)
12×2÷8=3(厘米)
答:三角形的高是3厘米。
20.解:3.14×2.52=19.625(平方米)
2.5+0.5=3(米)
3.14×3×2
=3.14×6
=18.84(米)
答:这个花坛占地19.625平方米,需要栏杆长18.84米。
21.解:6÷2=3(米)
3+2=5(米)
3.14×(52-32)
=3.14×(25-9)
=3.14×16
=50.24(平方米)
答:增加后花坛面积将比原来增加50.24平方米。
22.(1)解:3×60×60=10800(平方厘米)
答:这个镖盘的面积是10800平方厘米。
(2)解:60﹣40=20(厘米)
3×20×20÷10800≈11.1%
答:一等奖的中奖率是11.1%。
(3)解:将一等奖的中奖率调整到16%,
3×60×60×16%÷3
=36×16
=6×6×4×4
=(6×4)×(6×4)
=24×24
答:所以一等奖获奖区域圆的半径可以选24厘米。
23.解:1.6÷=2(米)
3.14×[(2÷2)2﹣(1.6÷2)2]
=3.14×[1﹣0.64]
=3.14×0.36
=1.1304
≈1.13(平方米)
答:大圆桌面积比小圆桌大约大1.13平方米。
24.解:100.48÷3.14÷2
=32÷2
=16(米)
6÷2=3(米)
3.14×(162-32)
=3.14×(256-9)
=3.14×247
=775.58(平方米)
答:这个养鱼池水域的占地面积是775.58平方米。
25.解:125.6÷3.14÷2
=40÷2
=20(米)
20+1=21(米)
3.14×(212-202)
=3.14×(441-400)
=3.14×41
=128.74(平方米)
答:小路的面积是128.74平方米。
26.解:正方形边长:18.84÷3=6.28(米)
正方形面积:6.28×6.28=39.4384(平方米)
半圆的半径:18.84×2÷3.14÷2=6(米)
半圆的面积:3.14×62÷2=56.52(平方米)
56.52>39.4384
答:围成半圆的面积大。
27.解:阴影部分圆心角为四边形内角和,即360度,所以阴影部分组合起来为一个圆,
半径:62.8÷3.14÷2=10(厘米)
阴影部分面积:10×10×3.14=314(平方厘米)
答:阴影部分的面积为314平方厘米。
28.(1)解:2+1×2+3.14×2÷2
=2+2+3.14
=7.14(cm)
(2)解:4×4-3.14×(4÷2)2
=16-3.14×4
=16-12.56
=3.44(cm2)
29.解:阴影部分的面积=×36-36÷2
=9×3.14-18
=28.26-18
=10.26(cm2)
答:阴影部分的面积是10.26cm2。
同课章节目录
