合情推理第三课时
图片预览






文档简介
课件24张PPT。2.1.1 合情推理(2)复习回顾:1.推理:从一个或几个已知命题得出另一个新命题的思维过程。推理前提结论---推理所依据的命题.---根据前提所得到的命题.类比推理归纳推理3、归纳推理的定义:归纳推理:概括、推广猜测一般性结论 简言之,归纳推理是由部分到整体、由个别到一般的推理。4、归纳推理的思维过程如下: 由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理,或者由个别事实推演出一般性的结论的推理,称为归纳推理(简称归纳).实验、观察5、归纳推理的一般模式:S1具有P,S2具有P,……Sn具有P,(S1,S2,…,Sn是A类事物的对象)所以A类事物具有P⑶ 检验猜想。⑵ 提出带有规律性的结论,即猜想;
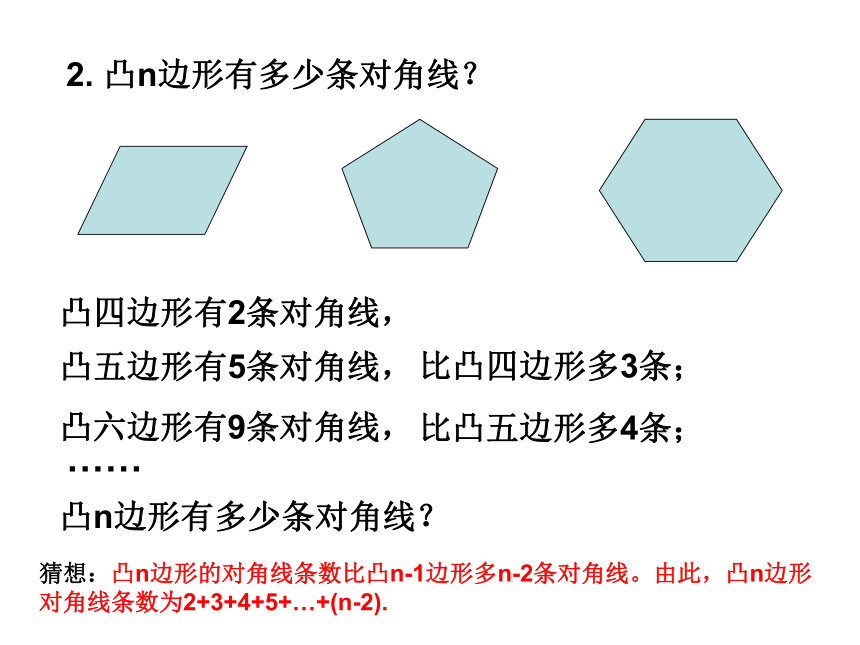
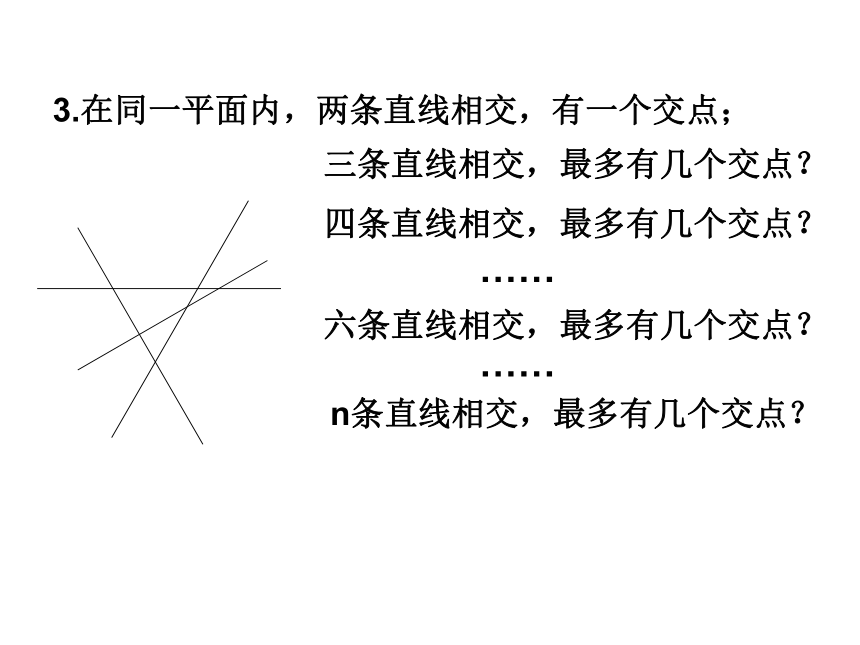
⑴ 对有限的资料进行观察、分析、归纳整理;6、归纳推理的一般步骤:1.归纳推理是依据特殊现象推断一般现象,因而,由归纳推理所得的结论超越了前提所包容的范围.2.归纳推理是依据若干已知的、没有穷尽的现象推断尚属未知的现象,因而结论具有猜测性.结论是否真实,还需经过逻辑证明和实践证明,因此它不能作为数学证明工具。3.归纳推理的前提是特殊的情况,因而归纳推理是立足于观察、经验和实验的基础之上.归纳推理是一种具有创造性的推理,通过归纳得到的猜想可作为进一步研究得起点,帮助人们发现问题和提出问题。7、归纳推理的几个特点:反例⑴ 归纳推理的结论不一定正确纠正典型错误1. 观察下列等式,并从中归纳出一般的结论:数学巩固:凸四边形有2条对角线,凸五边形有5条对角线,比凸四边形多3条;凸六边形有9条对角线,比凸五边形多4条;……猜想:凸n边形的对角线条数比凸n-1边形多n-2条对角线。由此,凸n边形对角线条数为2+3+4+5+…+(n-2).凸n边形有多少条对角线?2. 凸n边形有多少条对角线?3.在同一平面内,两条直线相交,有一个交点;三条直线相交,最多有几个交点?四条直线相交,最多有几个交点?……六条直线相交,最多有几个交点?……n条直线相交,最多有几个交点?2.1.1 合情推理(2)2.1 合情推理与演绎推理---- 从一个传说说起:春秋时代鲁国的公输班(后人称鲁班,被认为是木匠业的祖师)一次去林中砍树时被一株齿形的茅草割破了手,这桩倒霉事却使他发明了锯子.他的思路是这样的:茅草是齿形的;茅草能割破手.我需要一种能割断木头的工具;它也可以是齿形的.这个推理过程是归纳推理吗?情景创设1:相似点:绕太阳运转、绕轴自转、有大气层、有季节变换、大部
分时间的温度适合地球上的某些已知生物的生存等。地球上有生命火星上可能有生命上述推理是怎样的一个过程呢?(步骤)情景创设2:3.仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.4.利用平面向量的本定理类比得到空间向量的基本定理.情景创设: 类比推理:根据两个(或两类)对象之间在某些方面的相似或相同,推演出它们在其他方面也相似或相同,像这样的推理通常称为类比推理.(简称:类比)构建数学:类比推理的定义: 简言之,类比推理是由特殊到特殊的推理.类比推理的特点:1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.即类比推理是由特殊到特殊的推理.3.类比的结果是猜测性的不一定可靠,但它却有发现的功能.类比推理的一般步骤:⑴ 找出两类对象之间可以确切表述的相似特征;⑵ 用一类对象的已知特征去推测另一类对象的特征,
从而得出一个猜想;例1:试根据等式的性质猜想不等式的性质.等 式不等式解:等式与不等式有不少相似的属性,例如:问:这样猜想出的结论是否一定正确?数学应用:通过例1,你能得到类比推理的一般模式吗?类比推理的一般模式:所以B类事物可能具有性质d’.A类事物具有性质a,b,c,d,B类事物具有性质a’,b’,c’,(a,b,c与a’,b’,c’相似或相同)构建数学:例1:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.3个面两两垂直的四面体∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S归纳推理:归纳推理的前提是几个已知的特殊现象,归纳所得的结论是尚属未知的一般现象,该结论超越了前提所包容的范围,是从特殊到一般得命题的猜测,是否正确是需要证明的。类比推理:类比就是在两类不同的事物之间进行对比,找出若干相同或相似点之后,推测在其他方面也可以存在相同或相似之处的一种推理模式,类比推理是否正确是需要证明的。实验、观察概括、推广猜测一般性结论观察、比较联想、类推猜测新的结论 合情推理 归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理。 通俗地说,合情推理是指“合乎情理”的推理。 合情推理的应用 数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论。 证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向例2:如图有三根针和套在一根针上的若干金属片. 按下列规则,把金属片从一根针上全部移到另一根针上. 1.每次只能移动1个金属片; 2.较大的金属片不能放在较小的金属片上面.试推测;把n个金属片从1号针移到3号针,最少需要移动多少次?解;设an表示移动n块金属片时的移动次数.当n=1时,a1=1当n=2时,a2=3123当n=1时,a1=1当n=2时,a2=3解;设an表示移动n块金属片时的移动次数.当n=3时,a3=7当n=4时,a4=15猜想 an=2n -1123
⑴ 对有限的资料进行观察、分析、归纳整理;6、归纳推理的一般步骤:1.归纳推理是依据特殊现象推断一般现象,因而,由归纳推理所得的结论超越了前提所包容的范围.2.归纳推理是依据若干已知的、没有穷尽的现象推断尚属未知的现象,因而结论具有猜测性.结论是否真实,还需经过逻辑证明和实践证明,因此它不能作为数学证明工具。3.归纳推理的前提是特殊的情况,因而归纳推理是立足于观察、经验和实验的基础之上.归纳推理是一种具有创造性的推理,通过归纳得到的猜想可作为进一步研究得起点,帮助人们发现问题和提出问题。7、归纳推理的几个特点:反例⑴ 归纳推理的结论不一定正确纠正典型错误1. 观察下列等式,并从中归纳出一般的结论:数学巩固:凸四边形有2条对角线,凸五边形有5条对角线,比凸四边形多3条;凸六边形有9条对角线,比凸五边形多4条;……猜想:凸n边形的对角线条数比凸n-1边形多n-2条对角线。由此,凸n边形对角线条数为2+3+4+5+…+(n-2).凸n边形有多少条对角线?2. 凸n边形有多少条对角线?3.在同一平面内,两条直线相交,有一个交点;三条直线相交,最多有几个交点?四条直线相交,最多有几个交点?……六条直线相交,最多有几个交点?……n条直线相交,最多有几个交点?2.1.1 合情推理(2)2.1 合情推理与演绎推理---- 从一个传说说起:春秋时代鲁国的公输班(后人称鲁班,被认为是木匠业的祖师)一次去林中砍树时被一株齿形的茅草割破了手,这桩倒霉事却使他发明了锯子.他的思路是这样的:茅草是齿形的;茅草能割破手.我需要一种能割断木头的工具;它也可以是齿形的.这个推理过程是归纳推理吗?情景创设1:相似点:绕太阳运转、绕轴自转、有大气层、有季节变换、大部
分时间的温度适合地球上的某些已知生物的生存等。地球上有生命火星上可能有生命上述推理是怎样的一个过程呢?(步骤)情景创设2:3.仿照鱼类的外型和它们在水中沉浮的原理,发明了潜水艇.4.利用平面向量的本定理类比得到空间向量的基本定理.情景创设: 类比推理:根据两个(或两类)对象之间在某些方面的相似或相同,推演出它们在其他方面也相似或相同,像这样的推理通常称为类比推理.(简称:类比)构建数学:类比推理的定义: 简言之,类比推理是由特殊到特殊的推理.类比推理的特点:1.类比是从人们已经掌握了的事物的属性,推测正在研究的事物的属性,是以旧有的认识为基础,类比出新的结果.2.类比是从一种事物的特殊属性推测另一种事物的特殊属性.即类比推理是由特殊到特殊的推理.3.类比的结果是猜测性的不一定可靠,但它却有发现的功能.类比推理的一般步骤:⑴ 找出两类对象之间可以确切表述的相似特征;⑵ 用一类对象的已知特征去推测另一类对象的特征,
从而得出一个猜想;例1:试根据等式的性质猜想不等式的性质.等 式不等式解:等式与不等式有不少相似的属性,例如:问:这样猜想出的结论是否一定正确?数学应用:通过例1,你能得到类比推理的一般模式吗?类比推理的一般模式:所以B类事物可能具有性质d’.A类事物具有性质a,b,c,d,B类事物具有性质a’,b’,c’,(a,b,c与a’,b’,c’相似或相同)构建数学:例1:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.3个面两两垂直的四面体∠PDF=∠PDE=∠EDF=90°
4个面的面积S1,S2,S3和S
3个“直角面” S1,S2,S3和1个“斜面” S归纳推理:归纳推理的前提是几个已知的特殊现象,归纳所得的结论是尚属未知的一般现象,该结论超越了前提所包容的范围,是从特殊到一般得命题的猜测,是否正确是需要证明的。类比推理:类比就是在两类不同的事物之间进行对比,找出若干相同或相似点之后,推测在其他方面也可以存在相同或相似之处的一种推理模式,类比推理是否正确是需要证明的。实验、观察概括、推广猜测一般性结论观察、比较联想、类推猜测新的结论 合情推理 归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理。 通俗地说,合情推理是指“合乎情理”的推理。 合情推理的应用 数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论。 证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向例2:如图有三根针和套在一根针上的若干金属片. 按下列规则,把金属片从一根针上全部移到另一根针上. 1.每次只能移动1个金属片; 2.较大的金属片不能放在较小的金属片上面.试推测;把n个金属片从1号针移到3号针,最少需要移动多少次?解;设an表示移动n块金属片时的移动次数.当n=1时,a1=1当n=2时,a2=3123当n=1时,a1=1当n=2时,a2=3解;设an表示移动n块金属片时的移动次数.当n=3时,a3=7当n=4时,a4=15猜想 an=2n -1123
