青岛版九年级数学第一单元相似图形单元练习题(含答案)
文档属性
| 名称 | 青岛版九年级数学第一单元相似图形单元练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 159.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-19 21:49:51 | ||
图片预览


文档简介
青岛版九年级数学第一单元相似图形单元练习题(含答案)
一.选择题(共14小题)
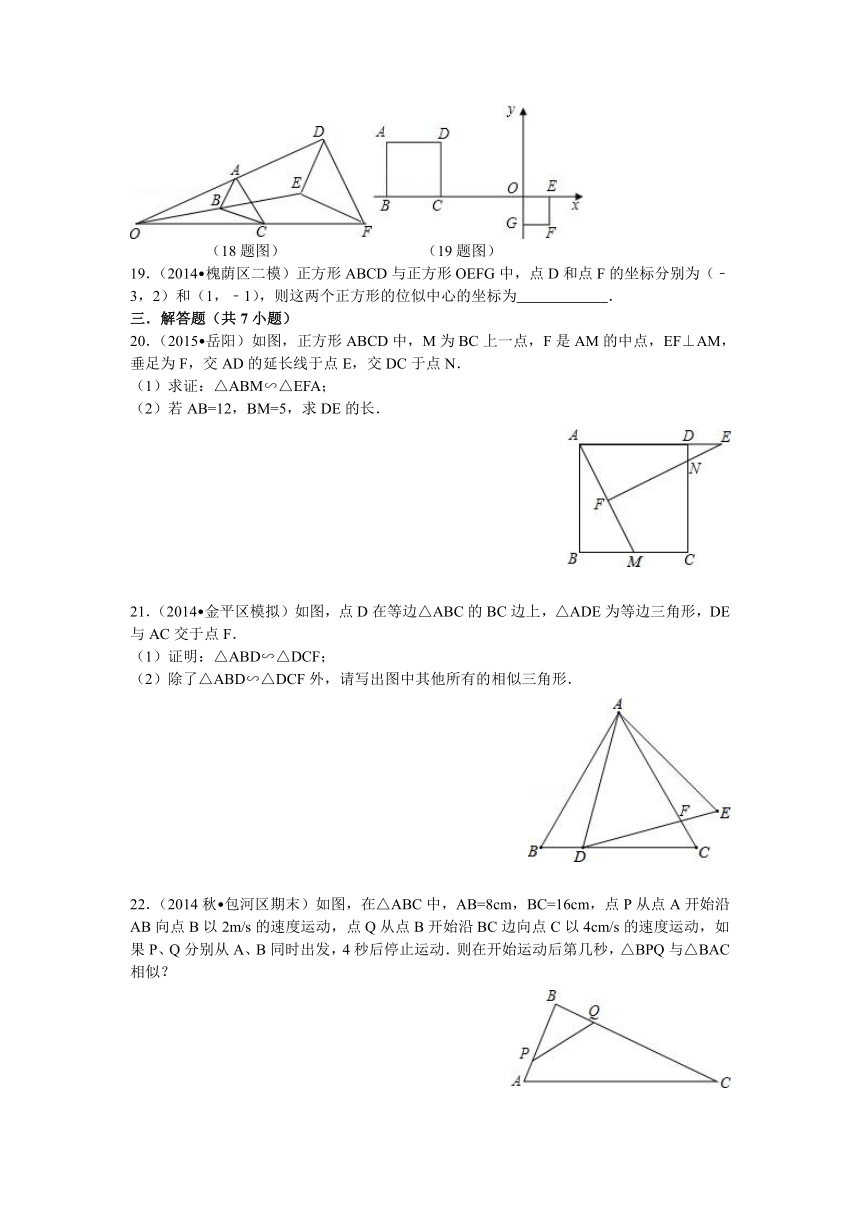
1.(2015 杭州模拟)如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )
A.10 B. 12 C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1题图) (4题图) (5题图)
2.(2015春 泰山区期末)如图所示, ( http: / / www.21cnjy.com )两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A. B. C. D.
3.(2014 江北区模拟)下面给出了一些关于相似的命题,其中真命题有( )
(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.
A.1 个 B. 2个 C. 3个 D. 4个
4.(2015 麻城市校级模拟)如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )
A.120m B. 100m C. 75m D. 25m
5.(2015 朝阳区一模)如图,为了估计 ( http: / / www.21cnjy.com )河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
A.40m B. 60m C. 120m D. 180m
6.(2015 舟山)如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A. B. 2 C. D.
7.(2015 三亚三模)如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则的值为( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(6题图) (7题图) (13题图) (14题图)
8.(2015 深圳校级模拟)若△ABC∽△DEF,且AB:DE=1:3,则S△ABC:S△DEF=( )
A.1:3 B. 1:9 C. 1: D. 1:1.5
9.(2015 富顺县一模)两个相似三角形对应中线的比2:3,周长的和是20,则两个三角形的周长分别为( )
A.8和12 B. 9和11 C. 7和13 D. 6和14
10.(2015 衡阳县一模)△ABC中, ( http: / / www.21cnjy.com )AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是( )
A.27 B. 12 C. 18 D. 20
11.(2015 重庆模拟)若△ABC∽△DEF,相似比为1:2,且△ABC的面积为2,则△DEF的面积为( )
A.16 B. 8 C. 4 D. 2
12.(2015 长宁区一模)如果两个相似三角形的面积比是1:6,则它们的相似比( )
A.1:36 B. 1:6 C. 1:3 D. 1:
13.(2015 锦州)如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C和D的坐标分别为( )
A.(2,2),(3,2) B.(2,4),(3,1) C.(2,2),(3,1) D.(3,1),(2,2)
14.(2015 营口)如 ( http: / / www.21cnjy.com )图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )
A.(4,2) B. (4,1) C. (5,2) D. (5,1)
二.填空题(共5小题)
15.(2015春 庆阳校级月考)图中的两个四边形相似,则x+y= ,a= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(15题图) (16题图)
16.(2015 新疆)如图,李明打网球时,球恰好打过网,且落在离网4m的位置上,则网球的击球的高度h为 .
17.(2015 本溪)在△ABC中, ( http: / / www.21cnjy.com )AB=6cm,AC=5cm,点D、E分别在AB、AC上.若△ADE与△ABC相似,且S△ADE:S四边形BCED=1:8,则AD= cm.
18.(2015 沈阳)如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AB:DE= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(18题图) (19题图)
19.(2014 槐荫区二模)正方 ( http: / / www.21cnjy.com )形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为 .
三.解答题(共7小题)
20.(2015 岳阳)如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
( http: / / www.21cnjy.com )
21.(2014 金平区模拟)如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
(1)证明:△ABD∽△DCF;
(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
( http: / / www.21cnjy.com )
22.(2014秋 包河区期末)如 ( http: / / www.21cnjy.com )图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?
( http: / / www.21cnjy.com )
23.(2013秋 蚌埠期末)如图,CD、BE分别是锐角△ABC中AB、AC边上的高线,垂足为D、E.
(1)证明:△ADC∽△AEB;
(2)连接DE,则△AED与△ABC能相似吗?说说你的理由.
( http: / / www.21cnjy.com )
24.(2014秋 德惠市期末)如图,△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加字母和线).
(2)请选择其中的一对三角形,说明其相似的理由.
( http: / / www.21cnjy.com )
25.(2014秋 高密市校级月考)已知:在△PAB中,AE⊥BP,BD⊥AP,求证:△PDE∽△PBA.
( http: / / www.21cnjy.com )
26.(2015 宁夏)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2:1.
( http: / / www.21cnjy.com )
青岛版九年级数学第一单元相似图形单元练习题参考答案
一.选择题(共14小题)
1.C.2.B.3.C.4.B.5.C.6.D.7.C.8.B.9.A.10.C.11.B.12.D.
13.C.14.C.
二.填空题(共5小题)
15.x+y= 63 ,a= 85° .16. 1.4 .17. 2或 18. 2:3
19. (﹣1,0)或(5,﹣2)
三.解答题(共7小题)
20.(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,∴∠AFE=90°,∴∠B=∠AFE,∴△ABM∽△EFA;
(2)解:∵∠B=90°,AB=12,BM=5,∴AM==13,AD=12,
∵F是AM的中点,∴AF=AM=6.5,
∵△ABM∽△EFA,∴,即,∴AE=16.9,∴DE=AE﹣AD=4.9.
21.(1)证明:∵△ABC,△ADE为等边三角形,∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,∴∠1=∠DFC,∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,∴△AEF∽△DCF,∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
( http: / / www.21cnjy.com )
22.解:设在开始运动后第x秒,△BPQ与△BAC相似,
由题意得:AP=2xcm,PB=(8﹣2x)cm,BQ=4x,
分两种情况考虑:
当∠BPQ=∠C,∠B=∠B时,△PBQ∽△CBA,
∴=,即=,
解得:x=0.8,
当x=0.8秒时,△BPQ与△BAC相似;
当∠BPQ=∠A,∠B=∠B时,△BPQ∽△BAC,
∴=,即=,
解得:x=2,
当x=2秒时,△BPQ与△BAC相似.
综上,当x=0.8秒或2秒时,△BPQ与△BAC相似.
23.(1)证明:∵如图,CD、BE分别是锐角△ABC中AB、AC边上的高线,
∴∠ADC=∠AEB=90°.
又∵∠A=∠A,∴△ADC∽△AEB;
(2)由(1)知,△ADC∽△AEB,则AD:AE=AC:AB.
又∵∠A=∠A,∴△AED∽△ABC.
24.(1)解:△ABC∽△ADE,△ABD∽△ACE;
(2)△ABD∽△ACE.
证明:由(1)知△ABC∽△ADE,∴=,∴AB×AE=AC×AD,∴=,
∵∠BAD=∠CAE,∴△ABD∽△ACE.
25.证明:∵在△PAB中,AE⊥BP,BD⊥AP,∴∠BDP=∠AEP,
又∵∠P=∠P,∴△PDB∽△PEA,∴=,又∵∠P=∠P,∴△PDE∽△PBA.
26.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
( http: / / www.21cnjy.com )
一.选择题(共14小题)
1.(2015 杭州模拟)如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )
A.10 B. 12 C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(1题图) (4题图) (5题图)
2.(2015春 泰山区期末)如图所示, ( http: / / www.21cnjy.com )两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A. B. C. D.
3.(2014 江北区模拟)下面给出了一些关于相似的命题,其中真命题有( )
(1)菱形都相似;(2)等腰直角三角形都相似;(3)正方形都相似;(4)矩形都相似;(5)正六边形都相似.
A.1 个 B. 2个 C. 3个 D. 4个
4.(2015 麻城市校级模拟)如图,测得BD=120m,DC=60m,EC=50m,则河宽AB为( )
A.120m B. 100m C. 75m D. 25m
5.(2015 朝阳区一模)如图,为了估计 ( http: / / www.21cnjy.com )河的宽度,在河的对岸选定一个目标点P,在近岸取点Q和S,使点P,Q,S在一条直线上,且直线PS与河垂直,在过点S且与PS垂直的直线a上选择适当的点T,PT与过点Q且与PS垂直的直线b的交点为R.如果QS=60m,ST=120m,QR=80m,则河的宽度PQ为( )
A.40m B. 60m C. 120m D. 180m
6.(2015 舟山)如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,AC与DF相交于点G,且AG=2,GB=1,BC=5,则的值为( )
A. B. 2 C. D.
7.(2015 三亚三模)如图所示,在△ABC中,DE∥BC,若AD=1,DB=2,则的值为( )
A. B. C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(6题图) (7题图) (13题图) (14题图)
8.(2015 深圳校级模拟)若△ABC∽△DEF,且AB:DE=1:3,则S△ABC:S△DEF=( )
A.1:3 B. 1:9 C. 1: D. 1:1.5
9.(2015 富顺县一模)两个相似三角形对应中线的比2:3,周长的和是20,则两个三角形的周长分别为( )
A.8和12 B. 9和11 C. 7和13 D. 6和14
10.(2015 衡阳县一模)△ABC中, ( http: / / www.21cnjy.com )AB=12,BC=18,CA=24,另一个和它相似的三角形最长的一边是36,则最短的一边是( )
A.27 B. 12 C. 18 D. 20
11.(2015 重庆模拟)若△ABC∽△DEF,相似比为1:2,且△ABC的面积为2,则△DEF的面积为( )
A.16 B. 8 C. 4 D. 2
12.(2015 长宁区一模)如果两个相似三角形的面积比是1:6,则它们的相似比( )
A.1:36 B. 1:6 C. 1:3 D. 1:
13.(2015 锦州)如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的后得到线段CD,则端点C和D的坐标分别为( )
A.(2,2),(3,2) B.(2,4),(3,1) C.(2,2),(3,1) D.(3,1),(2,2)
14.(2015 营口)如 ( http: / / www.21cnjy.com )图,△ABE和△CDE是以点E为位似中心的位似图形,已知点A(3,4),点C(2,2),点D(3,1),则点D的对应点B的坐标是( )
A.(4,2) B. (4,1) C. (5,2) D. (5,1)
二.填空题(共5小题)
15.(2015春 庆阳校级月考)图中的两个四边形相似,则x+y= ,a= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(15题图) (16题图)
16.(2015 新疆)如图,李明打网球时,球恰好打过网,且落在离网4m的位置上,则网球的击球的高度h为 .
17.(2015 本溪)在△ABC中, ( http: / / www.21cnjy.com )AB=6cm,AC=5cm,点D、E分别在AB、AC上.若△ADE与△ABC相似,且S△ADE:S四边形BCED=1:8,则AD= cm.
18.(2015 沈阳)如图,△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AB:DE= .
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
(18题图) (19题图)
19.(2014 槐荫区二模)正方 ( http: / / www.21cnjy.com )形ABCD与正方形OEFG中,点D和点F的坐标分别为(﹣3,2)和(1,﹣1),则这两个正方形的位似中心的坐标为 .
三.解答题(共7小题)
20.(2015 岳阳)如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
( http: / / www.21cnjy.com )
21.(2014 金平区模拟)如图,点D在等边△ABC的BC边上,△ADE为等边三角形,DE与AC交于点F.
(1)证明:△ABD∽△DCF;
(2)除了△ABD∽△DCF外,请写出图中其他所有的相似三角形.
( http: / / www.21cnjy.com )
22.(2014秋 包河区期末)如 ( http: / / www.21cnjy.com )图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB向点B以2m/s的速度运动,点Q从点B开始沿BC边向点C以4cm/s的速度运动,如果P、Q分别从A、B同时出发,4秒后停止运动.则在开始运动后第几秒,△BPQ与△BAC相似?
( http: / / www.21cnjy.com )
23.(2013秋 蚌埠期末)如图,CD、BE分别是锐角△ABC中AB、AC边上的高线,垂足为D、E.
(1)证明:△ADC∽△AEB;
(2)连接DE,则△AED与△ABC能相似吗?说说你的理由.
( http: / / www.21cnjy.com )
24.(2014秋 德惠市期末)如图,△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加字母和线).
(2)请选择其中的一对三角形,说明其相似的理由.
( http: / / www.21cnjy.com )
25.(2014秋 高密市校级月考)已知:在△PAB中,AE⊥BP,BD⊥AP,求证:△PDE∽△PBA.
( http: / / www.21cnjy.com )
26.(2015 宁夏)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2:1.
( http: / / www.21cnjy.com )
青岛版九年级数学第一单元相似图形单元练习题参考答案
一.选择题(共14小题)
1.C.2.B.3.C.4.B.5.C.6.D.7.C.8.B.9.A.10.C.11.B.12.D.
13.C.14.C.
二.填空题(共5小题)
15.x+y= 63 ,a= 85° .16. 1.4 .17. 2或 18. 2:3
19. (﹣1,0)或(5,﹣2)
三.解答题(共7小题)
20.(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,∴∠AFE=90°,∴∠B=∠AFE,∴△ABM∽△EFA;
(2)解:∵∠B=90°,AB=12,BM=5,∴AM==13,AD=12,
∵F是AM的中点,∴AF=AM=6.5,
∵△ABM∽△EFA,∴,即,∴AE=16.9,∴DE=AE﹣AD=4.9.
21.(1)证明:∵△ABC,△ADE为等边三角形,∴∠B=∠C=∠3=60°,
∴∠1+∠2=∠DFC+∠2,∴∠1=∠DFC,∴△ABD∽△DCF;
(2)解:∵∠C=∠E,∠AFE=∠DFC,∴△AEF∽△DCF,∴△ABD∽△AEF,
故除了△ABD∽△DCF外,图中相似三角形还有:△AEF∽△DCF,△ABD∽△AEF,△ABC∽△ADE,△ADF∽△ACD.
( http: / / www.21cnjy.com )
22.解:设在开始运动后第x秒,△BPQ与△BAC相似,
由题意得:AP=2xcm,PB=(8﹣2x)cm,BQ=4x,
分两种情况考虑:
当∠BPQ=∠C,∠B=∠B时,△PBQ∽△CBA,
∴=,即=,
解得:x=0.8,
当x=0.8秒时,△BPQ与△BAC相似;
当∠BPQ=∠A,∠B=∠B时,△BPQ∽△BAC,
∴=,即=,
解得:x=2,
当x=2秒时,△BPQ与△BAC相似.
综上,当x=0.8秒或2秒时,△BPQ与△BAC相似.
23.(1)证明:∵如图,CD、BE分别是锐角△ABC中AB、AC边上的高线,
∴∠ADC=∠AEB=90°.
又∵∠A=∠A,∴△ADC∽△AEB;
(2)由(1)知,△ADC∽△AEB,则AD:AE=AC:AB.
又∵∠A=∠A,∴△AED∽△ABC.
24.(1)解:△ABC∽△ADE,△ABD∽△ACE;
(2)△ABD∽△ACE.
证明:由(1)知△ABC∽△ADE,∴=,∴AB×AE=AC×AD,∴=,
∵∠BAD=∠CAE,∴△ABD∽△ACE.
25.证明:∵在△PAB中,AE⊥BP,BD⊥AP,∴∠BDP=∠AEP,
又∵∠P=∠P,∴△PDB∽△PEA,∴=,又∵∠P=∠P,∴△PDE∽△PBA.
26.解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求.
( http: / / www.21cnjy.com )
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
