人教版数学八年级下册同步练习18.1.1平行四边形的对角线性质(含答案)
文档属性
| 名称 | 人教版数学八年级下册同步练习18.1.1平行四边形的对角线性质(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 279.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 00:00:00 | ||
图片预览


文档简介
第2课时 平行四边形的对角线性质
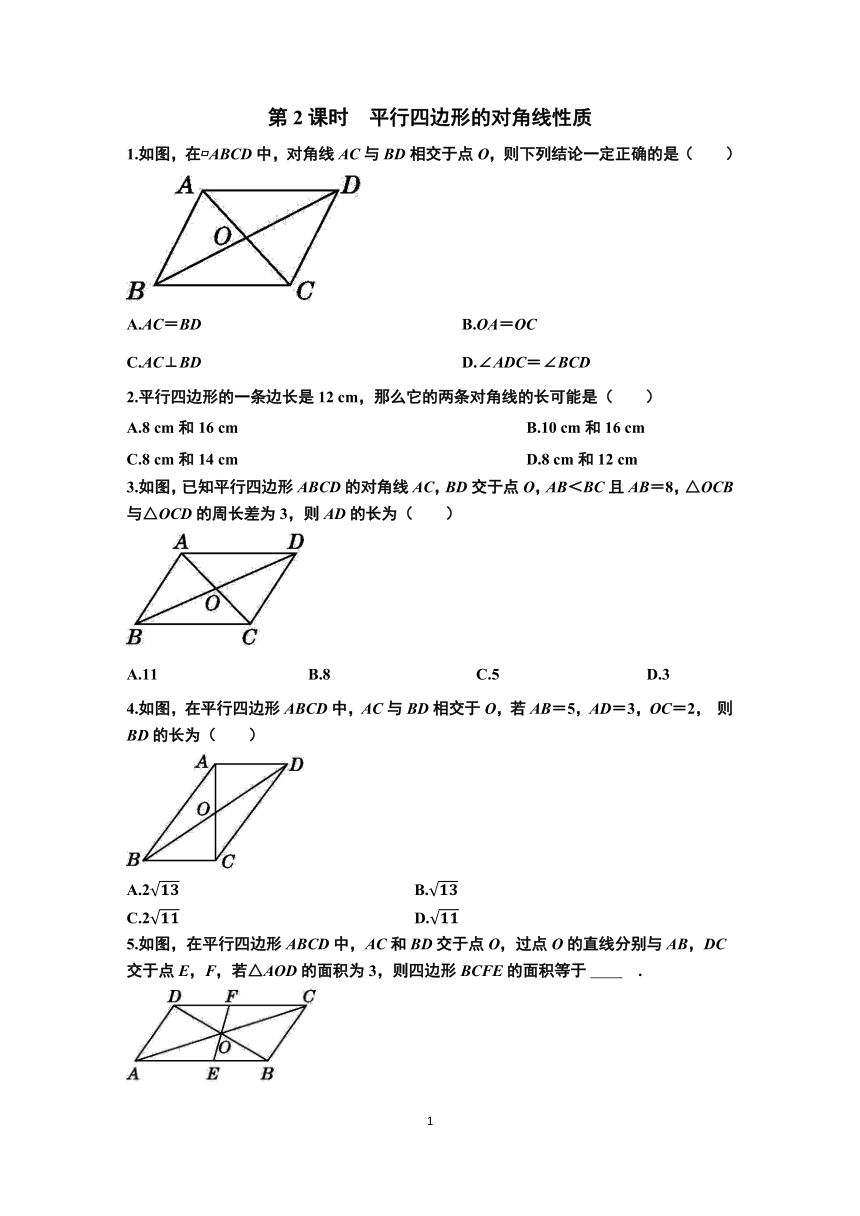
1.如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AC=BD B.OA=OC
C.AC⊥BD D.∠ADC=∠BCD
2.平行四边形的一条边长是12 cm,那么它的两条对角线的长可能是( )
A.8 cm和16 cm B.10 cm和16 cm
C.8 cm和14 cm D.8 cm和12 cm
3.如图,已知平行四边形ABCD的对角线AC,BD交于点O,AB<BC且AB=8,△OCB与△OCD的周长差为3,则AD的长为( )
A.11 B.8 C.5 D.3
4.如图,在平行四边形ABCD中,AC与BD相交于O,若AB=5,AD=3,OC=2, 则BD的长为( )
A.2 B.
C.2 D.
5.如图,在平行四边形ABCD中,AC和BD交于点O,过点O的直线分别与AB,DC交于点E,F,若△AOD的面积为3,则四边形BCFE的面积等于 .
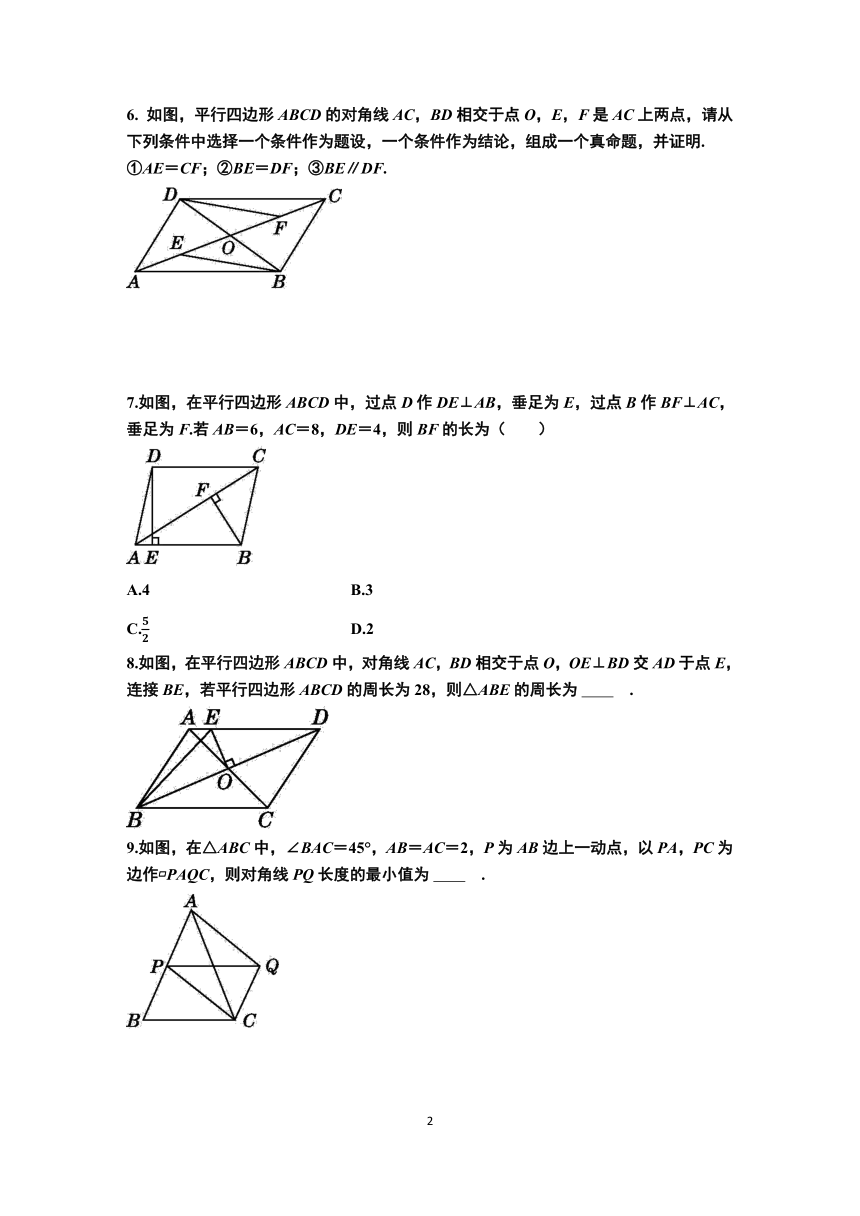
6. 如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F是AC上两点,请从下列条件中选择一个条件作为题设,一个条件作为结论,组成一个真命题,并证明.
①AE=CF;②BE=DF;③BE∥DF.
7.如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( )
A.4 B.3
C. D.2
8.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若平行四边形ABCD的周长为28,则△ABE的周长为 .
9.如图,在△ABC中,∠BAC=45°,AB=AC=2,P为AB边上一动点,以PA,PC为边作 PAQC,则对角线PQ长度的最小值为 .
10.按下列要求,用无刻度的直尺作图(请保留画图痕迹,不写作法).
如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,在图中画出∠AOB的平分线.
11.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:OE=OF.
(2)若△ABE的面积等于2,求△CFO的面积.
12.如图,在平行四边形ABCD中,过对角线AC与BD的交点O任意作一条直线l,分别交AD,BC于E,F两点.
(1)OE与OF相等吗?试说明理由.
(2)若直线l分别交BA和DC的延长线于点M,N,OM与ON相等吗?试说明理由.
(3)由(1)(2)你发现了什么?用语言表述出来.
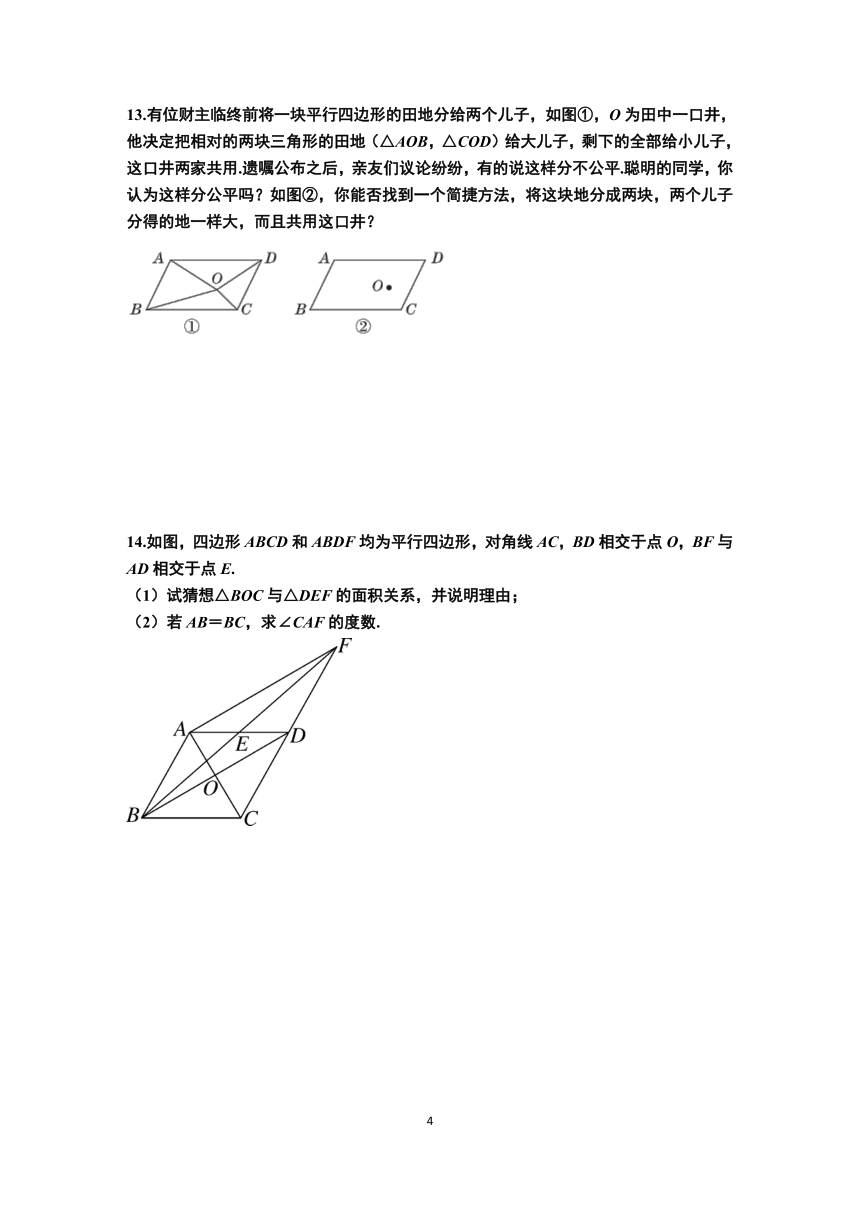
13.有位财主临终前将一块平行四边形的田地分给两个儿子,如图①,O为田中一口井,他决定把相对的两块三角形的田地(△AOB,△COD)给大儿子,剩下的全部给小儿子,这口井两家共用.遗嘱公布之后,亲友们议论纷纷,有的说这样分不公平.聪明的同学,你认为这样分公平吗?如图②,你能否找到一个简捷方法,将这块地分成两块,两个儿子分得的地一样大,而且共用这口井?
14.如图,四边形ABCD和ABDF均为平行四边形,对角线AC,BD相交于点O,BF与AD相交于点E.
(1)试猜想△BOC与△DEF的面积关系,并说明理由;
(2)若AB=BC,求∠CAF的度数.
15.如图,点O为 ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(点E,F不与端点重合),且DE=OF,连接AE,CF.
(1)求线段EF的长.
(2)若△OAE的面积为S1,△OCF的面积为S2,S1+S2的值是否发生变化?若不变,求出这个定值;若变化,请说明随着DE的增大,S1+S2的值是如何发生变化的.
1
参考答案
1.B 2.B 3.A 4.A 5.6
6.解:③作为题设,②作为结论.
证明:∵四边形ABCD是平行四边形,
∴OB=OD.
∵BE∥DF,∴∠FDO=∠EBO.
在△BOE和△DOF中,
∴△BOE≌△DOF(ASA),
∴BE=DF.
点拨:答案不唯一.
7.B
8.14 点拨:∵四边形ABCD是平行四边形,
∴OB=OD.
∵平行四边形ABCD的周长为28,∴AB+AD=14.
∵OE⊥BD,OB=OD,∴OE是线段BD的垂直平分线,
∴BE=ED,
∴△ABE的周长=AB+BE+AE=AB+ED+AE=AB+AD=14.
9. 点拨:设AC,PQ交于点O,如图所示.
∵四边形PAQC是平行四边形,
∴AO=CO,OP=OQ.
∴PO最短时PQ最短.
过点O作OP'⊥AB于点P'.∴当P在P'位置时OP最短.
∵∠BAC=45°,∴△AP'O是等腰直角三角形.
∵AO=AC=×2=1,∴OP'=AO=,
∴PQ的最小值=2OP'=.
10.解:如图所示,射线OP为∠AOB的平分线.
11.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD.
∵BE=FD,
∴OB-BE=OD-FD,即OE=OF.
(2)解:∵S△ABE=2,BE=EF,
∴S△AEF=S△ABE=2.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,AD∥BC.
∴∠ABE=∠CDF,∠ADF=∠CBE.
又∵BE=DF,
∴△ABE≌△CDF,△ADF≌△CBE.
∴∠AEB=∠CFD,∠AFD=∠CEB.
∴∠AEF=∠CFE,∠AFE=∠CEF.
∴AE∥CF,AF∥CE.
∴四边形AECF是平行四边形,
∴S△CFO=S△CEF=S△AEF=×2=1.
12.解:(1)OE=OF.理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC.
∴∠ODE=∠OBF.
在△ODE和△OBF中,
∴△ODE≌△OBF(ASA).
∴OE=OF.
(2)OM=ON.理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,AB∥CD.
∴∠OBM=∠ODN.
在△OBM和△ODN中,
∴△OBM≌△ODN(ASA).
∴OM=ON.
(3)过平行四边形两条对角线交点的任意一条直线和这个平行四边形的两组对边所在直线相交,所得每组对边所在直线的交点到对角线交点的距离相等.
13.解:如图①,过O作GH⊥AD交AD于点H,交BC于点G,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵GH⊥AD,∴GH⊥BC.
∴S△OAD+S△OBC=AD×OH+BC×OG=AD×GH=S平行四边形ABCD,
即△AOD和△COB的面积之和等于平行四边形ABCD的面积的一半.∴这样分公平.
如图②,作出平行四边形的两条对角线,过对角线的交点和O点的直线能将平行四边形田地分成面积相等的两部分,且共用这口井.
14.解:(1)△BOC与△DEF的面积相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.∴S△BOC=S ABCD.
同理,S△EDF=S ABDF.
又∵S ABCD=S ABDF=2S△ABD,
∴S△BOC=S△DEF.
(2)∵四边形ABCD是平行四边形,∴OA=OC.
又∵AB=BC,
∴AC⊥BD.
∴∠COD=90°.
∵四边形ABDF是平行四边形,∴AF∥BD.
∴∠CAF=∠COD=90°.
15.解:(1)∵点O为 ABCD的对角线AC,BD的交点,
∴OD=OB.
∵DE=OF,
∴EF=OD=BD=4.
(2)S1+S2的值不变.如图,连接AF,
∵点O为 ABCD的对角线AC,BD的交点,
∴AO=OC.
∴S1+S2=S△AOD.
∵DE=OF,∴S△ADE=S△AOF=S△COF.
∴S1+S2=S△AOD.
∵∠BCO=90°,∠BOC=60°,
∴∠DAC=90°,∠AOD=60°.∴AO=OD=2.
在Rt△AOD中,AD==2,
∴S1+S2=S△AOD=AD·OA=×2×2=2.
1.如图,在 ABCD中,对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AC=BD B.OA=OC
C.AC⊥BD D.∠ADC=∠BCD
2.平行四边形的一条边长是12 cm,那么它的两条对角线的长可能是( )
A.8 cm和16 cm B.10 cm和16 cm
C.8 cm和14 cm D.8 cm和12 cm
3.如图,已知平行四边形ABCD的对角线AC,BD交于点O,AB<BC且AB=8,△OCB与△OCD的周长差为3,则AD的长为( )
A.11 B.8 C.5 D.3
4.如图,在平行四边形ABCD中,AC与BD相交于O,若AB=5,AD=3,OC=2, 则BD的长为( )
A.2 B.
C.2 D.
5.如图,在平行四边形ABCD中,AC和BD交于点O,过点O的直线分别与AB,DC交于点E,F,若△AOD的面积为3,则四边形BCFE的面积等于 .
6. 如图,平行四边形ABCD的对角线AC,BD相交于点O,E,F是AC上两点,请从下列条件中选择一个条件作为题设,一个条件作为结论,组成一个真命题,并证明.
①AE=CF;②BE=DF;③BE∥DF.
7.如图,在平行四边形ABCD中,过点D作DE⊥AB,垂足为E,过点B作BF⊥AC,垂足为F.若AB=6,AC=8,DE=4,则BF的长为( )
A.4 B.3
C. D.2
8.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若平行四边形ABCD的周长为28,则△ABE的周长为 .
9.如图,在△ABC中,∠BAC=45°,AB=AC=2,P为AB边上一动点,以PA,PC为边作 PAQC,则对角线PQ长度的最小值为 .
10.按下列要求,用无刻度的直尺作图(请保留画图痕迹,不写作法).
如图,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,在图中画出∠AOB的平分线.
11.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F在对角线BD上,且BE=EF=FD,连接AE,EC,CF,FA.
(1)求证:OE=OF.
(2)若△ABE的面积等于2,求△CFO的面积.
12.如图,在平行四边形ABCD中,过对角线AC与BD的交点O任意作一条直线l,分别交AD,BC于E,F两点.
(1)OE与OF相等吗?试说明理由.
(2)若直线l分别交BA和DC的延长线于点M,N,OM与ON相等吗?试说明理由.
(3)由(1)(2)你发现了什么?用语言表述出来.
13.有位财主临终前将一块平行四边形的田地分给两个儿子,如图①,O为田中一口井,他决定把相对的两块三角形的田地(△AOB,△COD)给大儿子,剩下的全部给小儿子,这口井两家共用.遗嘱公布之后,亲友们议论纷纷,有的说这样分不公平.聪明的同学,你认为这样分公平吗?如图②,你能否找到一个简捷方法,将这块地分成两块,两个儿子分得的地一样大,而且共用这口井?
14.如图,四边形ABCD和ABDF均为平行四边形,对角线AC,BD相交于点O,BF与AD相交于点E.
(1)试猜想△BOC与△DEF的面积关系,并说明理由;
(2)若AB=BC,求∠CAF的度数.
15.如图,点O为 ABCD的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,点E是OD上的一动点,点F是OB上的一动点(点E,F不与端点重合),且DE=OF,连接AE,CF.
(1)求线段EF的长.
(2)若△OAE的面积为S1,△OCF的面积为S2,S1+S2的值是否发生变化?若不变,求出这个定值;若变化,请说明随着DE的增大,S1+S2的值是如何发生变化的.
1
参考答案
1.B 2.B 3.A 4.A 5.6
6.解:③作为题设,②作为结论.
证明:∵四边形ABCD是平行四边形,
∴OB=OD.
∵BE∥DF,∴∠FDO=∠EBO.
在△BOE和△DOF中,
∴△BOE≌△DOF(ASA),
∴BE=DF.
点拨:答案不唯一.
7.B
8.14 点拨:∵四边形ABCD是平行四边形,
∴OB=OD.
∵平行四边形ABCD的周长为28,∴AB+AD=14.
∵OE⊥BD,OB=OD,∴OE是线段BD的垂直平分线,
∴BE=ED,
∴△ABE的周长=AB+BE+AE=AB+ED+AE=AB+AD=14.
9. 点拨:设AC,PQ交于点O,如图所示.
∵四边形PAQC是平行四边形,
∴AO=CO,OP=OQ.
∴PO最短时PQ最短.
过点O作OP'⊥AB于点P'.∴当P在P'位置时OP最短.
∵∠BAC=45°,∴△AP'O是等腰直角三角形.
∵AO=AC=×2=1,∴OP'=AO=,
∴PQ的最小值=2OP'=.
10.解:如图所示,射线OP为∠AOB的平分线.
11.(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD.
∵BE=FD,
∴OB-BE=OD-FD,即OE=OF.
(2)解:∵S△ABE=2,BE=EF,
∴S△AEF=S△ABE=2.
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,AD=BC,AD∥BC.
∴∠ABE=∠CDF,∠ADF=∠CBE.
又∵BE=DF,
∴△ABE≌△CDF,△ADF≌△CBE.
∴∠AEB=∠CFD,∠AFD=∠CEB.
∴∠AEF=∠CFE,∠AFE=∠CEF.
∴AE∥CF,AF∥CE.
∴四边形AECF是平行四边形,
∴S△CFO=S△CEF=S△AEF=×2=1.
12.解:(1)OE=OF.理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC.
∴∠ODE=∠OBF.
在△ODE和△OBF中,
∴△ODE≌△OBF(ASA).
∴OE=OF.
(2)OM=ON.理由如下:
∵四边形ABCD是平行四边形,
∴OB=OD,AB∥CD.
∴∠OBM=∠ODN.
在△OBM和△ODN中,
∴△OBM≌△ODN(ASA).
∴OM=ON.
(3)过平行四边形两条对角线交点的任意一条直线和这个平行四边形的两组对边所在直线相交,所得每组对边所在直线的交点到对角线交点的距离相等.
13.解:如图①,过O作GH⊥AD交AD于点H,交BC于点G,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵GH⊥AD,∴GH⊥BC.
∴S△OAD+S△OBC=AD×OH+BC×OG=AD×GH=S平行四边形ABCD,
即△AOD和△COB的面积之和等于平行四边形ABCD的面积的一半.∴这样分公平.
如图②,作出平行四边形的两条对角线,过对角线的交点和O点的直线能将平行四边形田地分成面积相等的两部分,且共用这口井.
14.解:(1)△BOC与△DEF的面积相等.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.∴S△BOC=S ABCD.
同理,S△EDF=S ABDF.
又∵S ABCD=S ABDF=2S△ABD,
∴S△BOC=S△DEF.
(2)∵四边形ABCD是平行四边形,∴OA=OC.
又∵AB=BC,
∴AC⊥BD.
∴∠COD=90°.
∵四边形ABDF是平行四边形,∴AF∥BD.
∴∠CAF=∠COD=90°.
15.解:(1)∵点O为 ABCD的对角线AC,BD的交点,
∴OD=OB.
∵DE=OF,
∴EF=OD=BD=4.
(2)S1+S2的值不变.如图,连接AF,
∵点O为 ABCD的对角线AC,BD的交点,
∴AO=OC.
∴S1+S2=S△AOD.
∵DE=OF,∴S△ADE=S△AOF=S△COF.
∴S1+S2=S△AOD.
∵∠BCO=90°,∠BOC=60°,
∴∠DAC=90°,∠AOD=60°.∴AO=OD=2.
在Rt△AOD中,AD==2,
∴S1+S2=S△AOD=AD·OA=×2×2=2.
