六年级下册数学人教版正比例(课件)(共21张PPT)
文档属性
| 名称 | 六年级下册数学人教版正比例(课件)(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 281.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-29 21:43:00 | ||
图片预览






文档简介
(共21张PPT)
专题简介
1
1.成正比例的量:两种相关联的量,一种量变化,另一种量也随着发生变化,如果这两种量相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,用字母表示为: 。
2.判断两种量是否成正比例的方法:先找变量(相关联的量);再看定量(两种量的商是否一定);最后做出判断。
3.正比例关系的图像:是一条经过原点的直线。从图像中可以看到两种量的变化情况,不用计算,由一个量的值可以直接找到另一个量的对应值。
例题分析
2
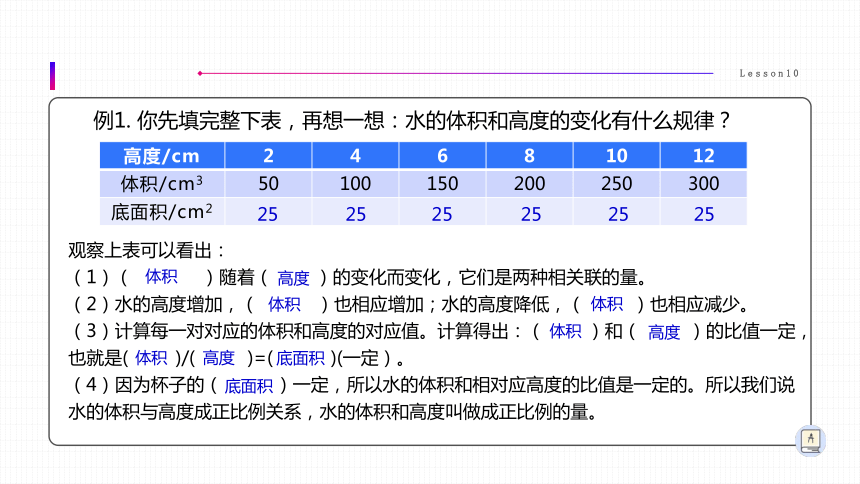
例1. 你先填完整下表,再想一想:水的体积和高度的变化有什么规律?
观察上表可以看出:
(1)( )随着( )的变化而变化,它们是两种相关联的量。
(2)水的高度增加,( )也相应增加;水的高度降低,( )也相应减少。
(3)计算每一对对应的体积和高度的对应值。计算得出:( )和( )的比值一定,也就是( )/( )=( )(一定)。
(4)因为杯子的( )一定,所以水的体积和相对应高度的比值是一定的。所以我们说水的体积与高度成正比例关系,水的体积和高度叫做成正比例的量。
体积
高度
体积
体积
体积
高度
体积
高度
底面积
高度/cm 2 4 6 8 10 12
体积/cm3 50 100 150 200 250 300
底面积/cm2
25
25
25
25
25
25
底面积
例2. 列举生活中成正比例关系的量。
(1)如果长方形的宽一定,那么长方形的( )和( )成正比例;
(2)如果速度一定,那么( )和( )成正比例;
(3)每天生产的零件数一定,生产的零件( )和生产的( )成正比例。
面积
长
路程
时间
总数
天数
精选例题3. 想一想,填一填,并回答问题。
正方形的周长和边长成正比例关系吗?为什么?
答:正方形的周长和边长成正比例关系,因为正方形的周长与边长的比值不变,都等于4.
学霸笔记
先找变量,再找不变量
商(比值)一定,成正比
正方形的边长(cm) 1 2 3 4 5 ……
正方形的周长(cm) ……
4
8
12
16
20
精选例题4.
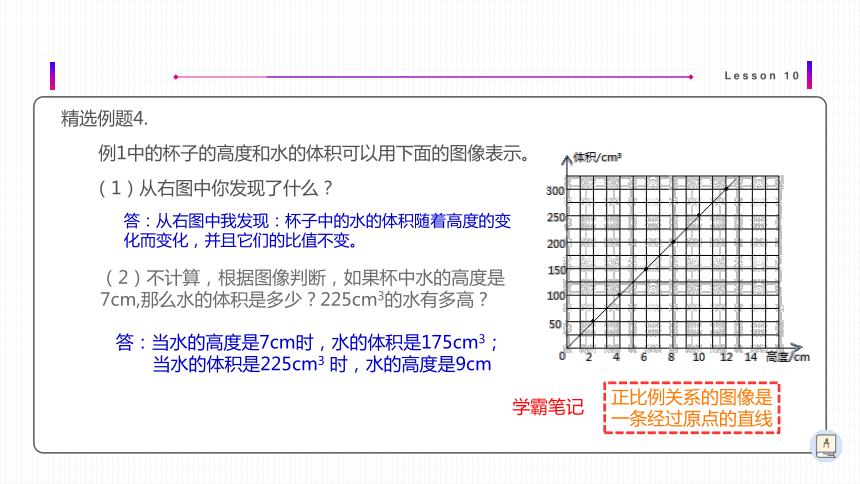
例1中的杯子的高度和水的体积可以用下面的图像表示。
(1)从右图中你发现了什么?
答:从右图中我发现:杯子中的水的体积随着高度的变化而变化,并且它们的比值不变。
(2)不计算,根据图像判断,如果杯中水的高度是7cm,那么水的体积是多少?225cm3的水有多高?
答:当水的高度是7cm时,水的体积是175cm3;
当水的体积是225cm3 时,水的高度是9cm
学霸笔记
正比例关系的图像是一条经过原点的直线
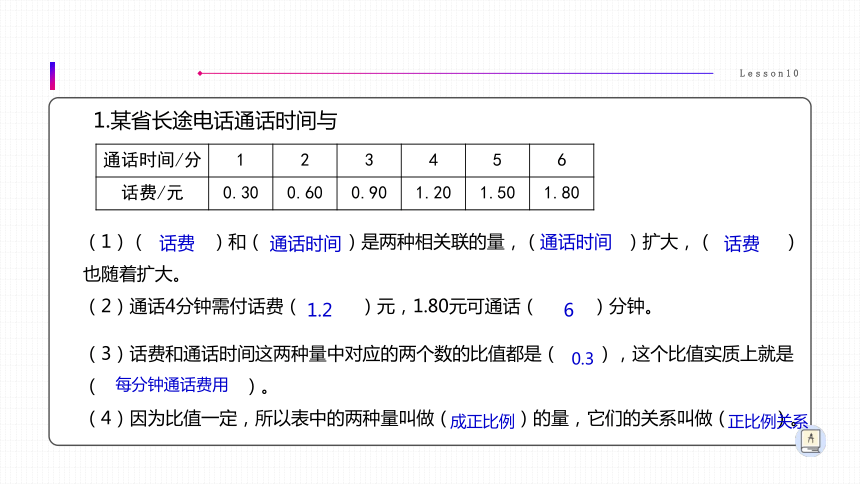
1.某省长途电话通话时间与
通话时间/分 1 2 3 4 5 6
话费/元 0.30 0.60 0.90 1.20 1.50 1.80
(1)( )和( )是两种相关联的量,( )扩大,( )也随着扩大。
(2)通话4分钟需付话费( )元,1.80元可通话( )分钟。
话费
通话时间
通话时间
话费
1.2
6
(3)话费和通话时间这两种量中对应的两个数的比值都是( ),这个比值实质上就是( )。
(4)因为比值一定,所以表中的两种量叫做( )的量,它们的关系叫做( )。
0.3
每分钟通话费用
成正比例
正比例关系
二、我会判。
( )1.如果 3x=8y,那么 y 与 x 成正比例。
( )2.如果14/x = 20/y ,那么 y 和 x 成正比例。
( )3.一个加数不变,和与另一个加数成正比例。
( )4.圆的周长和半径成正比例。
√
y÷x=3/8
√
y÷x=10/7
×
加减不成比例
√
C÷r=2Π
三、我会选。
1. 下面各题中的两种量不成正比例的是( )。
A、一个儿童的身高与体重 B、比值一定,比的前项和后项
C、三角形的底一定,它的面积和高 D、日产量一定,生产总量和完成天数
2. 表示 x 和 y 不是正比例关系的式子是( )。
A、y/x=k(k 一定) B、xy=k(k 一定)
C、x=yk(k 一定) D、y=xk(k 一定)
A
B
三、我会选。
3. 下面成正比例关系的是( )。
A、长方形的长一定,它的宽和周长
B、水桶的底面积一定,水的高度和水的体积
C、实验室铺地砖,每块砖的面积和需要的块数
D、圆的半径和面积
4. 正方形的周长和它的边长( )。
A、成正比例 B、成反比例 C、不成比例
B
A
四. 一种花布的数量和总价如下表。
数量/m 1 2 3 4 5 6 7 …
总价/元 8 16 24 32 40 48 56 …
(1)分别写出各组总价和相对应的数量的比,并求出比值。
(2)说明这个比值所表示的意义。
(3)表中的总价和数量成正比例吗?为什么?
答:8:1=16:2=24:3=32:4=40:5=48:6=56:7=8。
答:这个比值表示这种花布的单价是8元。
答:表中的总价和数量成正比例,因为总价÷数量=单价(一定)。
五. 看图像把表格填完整。
10
4
6
15
8
20
10
25
五. 看图像把表格填完整。
1. 根据上面的表格,求三角形的高。
2. 当三角形的底是12时,三角形的面积是多少?
3. 当三角形的底是7cm时,三角形的面积是多少?并在图像上描出这一点的大致位置。
h=2S/a=2×5÷2=5(cm)
S=ah÷2=12×5÷2=30(cm2)
7×5÷2=17.5(cm2)
●
1.设一个量x与另一个量y成正比例关系,已知当x=6时,y=4.
(1)写出y和x的关系式 (2)求出当x=6.9时,y的值
x:y=6:4
6.9:y=6:4
解得 y=4.6
2.选择。
(1)和圆的面积成正比例的量是( )
A、半径 B、半径的平方 C、直径
(2)因为圆周率一定,所以在圆中成正比例的量是( )
A、面积和直径 B、面积和半径 C、周长和直径
(3)下列算式中,X与Y成正比例关系的是( )
A、X+6=Y B、6X=Y C、6÷X=Y
B
C
B
3.判断
(1)分数的分子一定,分数值和分母成正比例。( )
(2)铺地面积一定,方砖的边长和所需块数成正比例。( )
(3)圆的周长和直径成正比例。( )
(4)除数一定,被除数和商成正比例。( )
(5)和一定,加数和另一个加数成正比例。( )
×
×
√
√
×
1. 如果 3A=1.5B(A≠0),那么 A 与 B 成(______)比例,A 与 B 的最简整数比是(__________)。
2.一根木头长 24 分米,要锯成 4 分米长的木棍,每锯一次要 3 分钟,锯完一段休息 2 分 钟,全部锯完需要多少分钟?
正
1: 2
次数:24÷4-1=5(次)
锯木时间:5×3=15(分钟)
休息时间:(5-1)×2=8(分钟)
共:15+8=23(分钟)
答:全部锯完需要23分钟。
3. 甲、乙两人同时从 A、B 两地相向而行,第一次在离 A 地 40 千米处相遇,之后两 人仍以原速度前进,各自到达目的地后,立即返回,又在离 A 地 20 千米处相遇,则 AB 两地距离为多少千米?
2个全程:40×3+20=140(km)
AB距离:140÷2=70(km)
答:AB 两地距离70千米。
40km
c
20km
40km
40km
再 见
专题简介
1
1.成正比例的量:两种相关联的量,一种量变化,另一种量也随着发生变化,如果这两种量相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系,用字母表示为: 。
2.判断两种量是否成正比例的方法:先找变量(相关联的量);再看定量(两种量的商是否一定);最后做出判断。
3.正比例关系的图像:是一条经过原点的直线。从图像中可以看到两种量的变化情况,不用计算,由一个量的值可以直接找到另一个量的对应值。
例题分析
2
例1. 你先填完整下表,再想一想:水的体积和高度的变化有什么规律?
观察上表可以看出:
(1)( )随着( )的变化而变化,它们是两种相关联的量。
(2)水的高度增加,( )也相应增加;水的高度降低,( )也相应减少。
(3)计算每一对对应的体积和高度的对应值。计算得出:( )和( )的比值一定,也就是( )/( )=( )(一定)。
(4)因为杯子的( )一定,所以水的体积和相对应高度的比值是一定的。所以我们说水的体积与高度成正比例关系,水的体积和高度叫做成正比例的量。
体积
高度
体积
体积
体积
高度
体积
高度
底面积
高度/cm 2 4 6 8 10 12
体积/cm3 50 100 150 200 250 300
底面积/cm2
25
25
25
25
25
25
底面积
例2. 列举生活中成正比例关系的量。
(1)如果长方形的宽一定,那么长方形的( )和( )成正比例;
(2)如果速度一定,那么( )和( )成正比例;
(3)每天生产的零件数一定,生产的零件( )和生产的( )成正比例。
面积
长
路程
时间
总数
天数
精选例题3. 想一想,填一填,并回答问题。
正方形的周长和边长成正比例关系吗?为什么?
答:正方形的周长和边长成正比例关系,因为正方形的周长与边长的比值不变,都等于4.
学霸笔记
先找变量,再找不变量
商(比值)一定,成正比
正方形的边长(cm) 1 2 3 4 5 ……
正方形的周长(cm) ……
4
8
12
16
20
精选例题4.
例1中的杯子的高度和水的体积可以用下面的图像表示。
(1)从右图中你发现了什么?
答:从右图中我发现:杯子中的水的体积随着高度的变化而变化,并且它们的比值不变。
(2)不计算,根据图像判断,如果杯中水的高度是7cm,那么水的体积是多少?225cm3的水有多高?
答:当水的高度是7cm时,水的体积是175cm3;
当水的体积是225cm3 时,水的高度是9cm
学霸笔记
正比例关系的图像是一条经过原点的直线
1.某省长途电话通话时间与
通话时间/分 1 2 3 4 5 6
话费/元 0.30 0.60 0.90 1.20 1.50 1.80
(1)( )和( )是两种相关联的量,( )扩大,( )也随着扩大。
(2)通话4分钟需付话费( )元,1.80元可通话( )分钟。
话费
通话时间
通话时间
话费
1.2
6
(3)话费和通话时间这两种量中对应的两个数的比值都是( ),这个比值实质上就是( )。
(4)因为比值一定,所以表中的两种量叫做( )的量,它们的关系叫做( )。
0.3
每分钟通话费用
成正比例
正比例关系
二、我会判。
( )1.如果 3x=8y,那么 y 与 x 成正比例。
( )2.如果14/x = 20/y ,那么 y 和 x 成正比例。
( )3.一个加数不变,和与另一个加数成正比例。
( )4.圆的周长和半径成正比例。
√
y÷x=3/8
√
y÷x=10/7
×
加减不成比例
√
C÷r=2Π
三、我会选。
1. 下面各题中的两种量不成正比例的是( )。
A、一个儿童的身高与体重 B、比值一定,比的前项和后项
C、三角形的底一定,它的面积和高 D、日产量一定,生产总量和完成天数
2. 表示 x 和 y 不是正比例关系的式子是( )。
A、y/x=k(k 一定) B、xy=k(k 一定)
C、x=yk(k 一定) D、y=xk(k 一定)
A
B
三、我会选。
3. 下面成正比例关系的是( )。
A、长方形的长一定,它的宽和周长
B、水桶的底面积一定,水的高度和水的体积
C、实验室铺地砖,每块砖的面积和需要的块数
D、圆的半径和面积
4. 正方形的周长和它的边长( )。
A、成正比例 B、成反比例 C、不成比例
B
A
四. 一种花布的数量和总价如下表。
数量/m 1 2 3 4 5 6 7 …
总价/元 8 16 24 32 40 48 56 …
(1)分别写出各组总价和相对应的数量的比,并求出比值。
(2)说明这个比值所表示的意义。
(3)表中的总价和数量成正比例吗?为什么?
答:8:1=16:2=24:3=32:4=40:5=48:6=56:7=8。
答:这个比值表示这种花布的单价是8元。
答:表中的总价和数量成正比例,因为总价÷数量=单价(一定)。
五. 看图像把表格填完整。
10
4
6
15
8
20
10
25
五. 看图像把表格填完整。
1. 根据上面的表格,求三角形的高。
2. 当三角形的底是12时,三角形的面积是多少?
3. 当三角形的底是7cm时,三角形的面积是多少?并在图像上描出这一点的大致位置。
h=2S/a=2×5÷2=5(cm)
S=ah÷2=12×5÷2=30(cm2)
7×5÷2=17.5(cm2)
●
1.设一个量x与另一个量y成正比例关系,已知当x=6时,y=4.
(1)写出y和x的关系式 (2)求出当x=6.9时,y的值
x:y=6:4
6.9:y=6:4
解得 y=4.6
2.选择。
(1)和圆的面积成正比例的量是( )
A、半径 B、半径的平方 C、直径
(2)因为圆周率一定,所以在圆中成正比例的量是( )
A、面积和直径 B、面积和半径 C、周长和直径
(3)下列算式中,X与Y成正比例关系的是( )
A、X+6=Y B、6X=Y C、6÷X=Y
B
C
B
3.判断
(1)分数的分子一定,分数值和分母成正比例。( )
(2)铺地面积一定,方砖的边长和所需块数成正比例。( )
(3)圆的周长和直径成正比例。( )
(4)除数一定,被除数和商成正比例。( )
(5)和一定,加数和另一个加数成正比例。( )
×
×
√
√
×
1. 如果 3A=1.5B(A≠0),那么 A 与 B 成(______)比例,A 与 B 的最简整数比是(__________)。
2.一根木头长 24 分米,要锯成 4 分米长的木棍,每锯一次要 3 分钟,锯完一段休息 2 分 钟,全部锯完需要多少分钟?
正
1: 2
次数:24÷4-1=5(次)
锯木时间:5×3=15(分钟)
休息时间:(5-1)×2=8(分钟)
共:15+8=23(分钟)
答:全部锯完需要23分钟。
3. 甲、乙两人同时从 A、B 两地相向而行,第一次在离 A 地 40 千米处相遇,之后两 人仍以原速度前进,各自到达目的地后,立即返回,又在离 A 地 20 千米处相遇,则 AB 两地距离为多少千米?
2个全程:40×3+20=140(km)
AB距离:140÷2=70(km)
答:AB 两地距离70千米。
40km
c
20km
40km
40km
再 见
