6.2.2 矩形的判定同步练习(含答案)
文档属性
| 名称 | 6.2.2 矩形的判定同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 08:45:52 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
2 矩形的性质与判定
第2课时 矩形的判定
基 础 练
练点1 由对角线的关系判定矩形
1.在下列条件中,能够判定 ABCD 为矩形的是( )
A. AB=AC B. AC⊥BD C. AB=AD D. AC =BD
2.如图,在平行四边形ABCD 中,M,N是 BD 上两点,BM =DN,连接AM,MC,CN,NA,添加一个条件,使四边形 AMCN是矩形,这个条件是( )
B. MB=MO C. BD⊥AC D.∠AMB=∠CND
(第2 题) (第3题)
练点2 由直角的个数判定矩形
3.如图,在四边形ABCD中,AB∥DC,AD∥BC, 在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是____________.
4.如图,在 ABCD中, ∠ACB=90°,过点 D 作DE⊥BC 交 BC 的延长线于点E. 求证:四边形ACED 是矩形.
5.如图,已知菱形ABCD的对角线AC,BD 交于点O,∥∥求证:四边形 OCED 是矩形.
纠易错 对矩形的判定方法理解错误导致出错
6.在一组对边平行的四边形中,下列条件中,可判定这个四边形是矩形的是( )
A.另一组对边相等,对角线相等 B.另一组对边相等,对角线互相垂直
C.另一组对边平行,对角线相等 D.另一组对边平行,对角线互相垂直
提 升 练
7.在四边形ABCD中, ∥下列条件能使四边形 ABCD 为矩形的是( )
A. AB∥CD
8.要检验一个四边形的桌面是否为矩形,可行的测量方案是( )
A.测量两条对角线是否相等
B.度量两个角是否是
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
9.如图,□ABCD的对角线 AC,BD 相交于点O,添加下列条件仍不能判定四边形 ABCD 是矩形的是( )
(第9 题) (第 10题)
10.如图,在四边形 ABCD 中, AD=10 cm,BC=8 cm ,点P从点D出发,以1 cm/s的速度向点 A 运动,点 M 从点 B 同时出发,以相同的速度向点 C 运动,当其中一个动点到达终点时,两个动点同时停止运动.设点P 的运动时间为 t(单位:s),下列结论正确的是( )
A. 当t =4时,四边形ABMP 为矩形 B.当t=5时,四边形CDPM为平行四边形
C.当CD=PM时,t=4 D.当CD=PM 时,t=4 或6
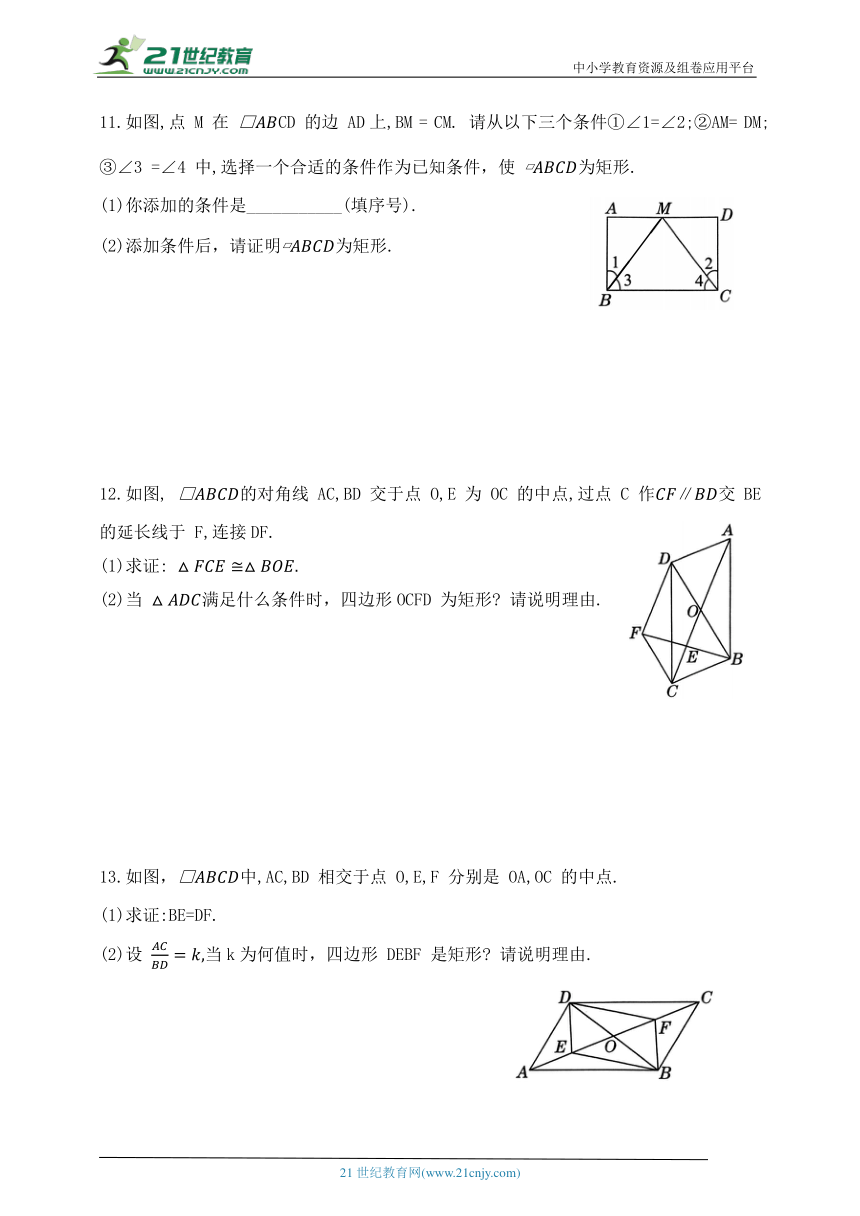
11.如图,点 M 在 CD 的边 AD上,BM = CM. 请从以下三个条件①∠1=∠2;②AM= DM;③∠3 =∠4 中,选择一个合适的条件作为已知条件,使 为矩形.
(1)你添加的条件是___________(填序号).
(2)添加条件后,请证明为矩形.
12.如图, 的对角线AC,BD 交于点 O,E为 OC 的中点,过点 C 作∥交BE的延长线于 F,连接DF.
(1)求证:
(2)当 满足什么条件时,四边形OCFD 为矩形 请说明理由.
13.如图,中,AC,BD 相交于点 O,E,F 分别是 OA,OC 的中点.
(1)求证:BE=DF.
(2)设 当k为何值时,四边形 DEBF 是矩形 请说明理由.
参考答案
1. D
2. A 【点拨】∵四边形ABCD是平行四边形,∴ OA=OC,OB =OD.
∵ BM=DN,∴OB-BM=OD-DN , 即OM = ON,∴ 四边形 AMCN 是平行四边形.
∴四边形AMCN是矩形.
3.∠A=90°(答案不唯一)
4.【证明】∵四边形ABCD为平行四边形,∴AD∥BC, ∴∠DAC=∠ACB =90°.
∵DE⊥BC,∴ ∠E=90°.
又∵∠ACE = 180°-∠ACB = 90°,∴ ∠ACE =∠DAC=∠E=90°,
∴四边形ACED 是矩形.
5.【证明】∵CE∥OD,DE∥OC,∴ 四边形OCED是平行四边形.
∵ 四边形 ABCD 是菱形,∴AC⊥BD,∴∠DOC=90°,∴ OCED是矩形.
点方法 证明四边形是矩形的方法:(1) 如果四边形是平行四边形, 可考虑有一个角是直角或对角线相等;(2) 如果四边形有一个角是直角或对角线相等, 可考虑证明四边形是平行四边形;(3) 证明四边形有3个角是直角.
6. C
点易错 此题易因对矩形的判定方法理解错误而出错.在一组对边平行的前提下, 再找该组对边相等或另一组对边平行即可判定这个四边形为平行四边形, 再结合对角线相等即可判定这个四边形是矩形.
7. C 【点拨】A.∵ AB∥CD,AD∥BC,∴ 四边形ABCD是平行四边形,由AB =CD不能判定四边形ABCD为矩形. B.∵AD=BC,AD∥BC,∴ 四边形ABCD 是平行四边形,由AB=CD不能判定四边形 ABCD为矩形. C.∵AD∥BC,∴∠A +∠B=180°.∵∠A=的长为 AD与 BC 间的距离.∵AB=CD,∴CD⊥BC,∴∠C=∠D=90°,∴四边形ABCD是矩形. D.∵AD∥BC,∴∠A+∠B=180°,∠D+∠C=180°.∵∠A =∠D,∴ ∠B=∠C.∵ AB=CD,∴当AD≠BC 时,四边形ABCD 是等腰梯形.
8. C 【点拨】A.对角线相等的四边形不一定是平行四边形,更不能判定其为矩形;B.两个角是 的四边形不一定是矩形,三个角是 的四边形才是矩形;C.由对角线的交点到四个顶点的距离相等,可知四边形的对角线互相平分且对角线相等,所以可判定是矩形;D.两组对边相等的四边形是平行四边形,不能判定其为矩形.
9. B 【点拨】 ∴□ABCD为矩形;B.∵AB =AD,∴□ABCD 为菱形;C.∵四边形ABCD 是平行四边形,∴OA =OC,OB=OD.∵ OA =OD,∴ AC =BD,∴□ABCD 是矩形;D. ∵四边形 ABCD是平行四边形,∴ ∠ABC=∠ADC. ∵ ∠ABC +∠ADC = 180°,∴ ∠ABC=∠ADC=90°,∴ ABCD为矩形.
10. D 【点拨】∵∠A=∠B=90°,∴AD∥BC.根据题意,得DP=t cm,BM =t cm,∵ AD =10 cm,BC =8cm ,∴AP=(10-t) cm,CM=(8-t) cm.当四边形ABMP为矩形时,AP=BM,即10-t=t,解得t=5,故A 错误;当四边形 CDPM 为平行四边形时,DP =CM,即t=8-t,解得 t=4,故 B 错误;当 PM 时,分两种情况:①四边形CDPM 是平行四边形,此时CM=PD,即8-t=t,解得 t=4;②四边形CDPM 是等腰梯形,过点M作MG⊥AD于点G,过点C 作CH⊥AD于点H,则 GH = CM,AG = BM,GM = HC,∠MGP = ∠CHD = 90°. ∵ PM = CD, ∴ Rt△MGP≌Rt△CHD(HL),∴GP = HD,∴ AG= 又∵ BM=tcm,∴t=6.综上,当CD=PM 时,t =4 或6,故C 错误,D正确.
11.(1)① (2)【证明】∵ 四边形ABCD是平行四边形,
∴ AB∥DC,AB = DC,∴ ∠A +∠D =180°.
在△ABM 和△DCM 中,
为矩形.
【点拨】 本题答案不唯一.
(1)【证明】∵ CF∥BD,∴∠CFE=∠OBE.∵ E为OC 的中点,
在 和 中,
(2)【解】当 满足AD=CD时,四边形OCFD为矩形.理由如下:
∵△FCE≌△BOE,∴ CF=OB.
∵四边形ABCD 是平行四边形, OD.∴CF=OD.
又∵CF∥BD,∴四边形OCFD为平行四边形.
∴∠COD=90°.∴ 四边形OCFD 为矩形.
13.(1)【证明】∵ 四边形ABCD是平行四边形, ∴BO=OD,AO=OC.
∵E,F 分别为AO,OC 的中点,
∴ 四边形DEBF 是平行四边形,
(2)【解】当 时,四边形DEBF 是矩形.理由如下:
.
∵四边形DEBF 是平行四边形.∴四边形DEBF 是矩形.
∴ 当 时,四边形DEBF 是矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
2 矩形的性质与判定
第2课时 矩形的判定
基 础 练
练点1 由对角线的关系判定矩形
1.在下列条件中,能够判定 ABCD 为矩形的是( )
A. AB=AC B. AC⊥BD C. AB=AD D. AC =BD
2.如图,在平行四边形ABCD 中,M,N是 BD 上两点,BM =DN,连接AM,MC,CN,NA,添加一个条件,使四边形 AMCN是矩形,这个条件是( )
B. MB=MO C. BD⊥AC D.∠AMB=∠CND
(第2 题) (第3题)
练点2 由直角的个数判定矩形
3.如图,在四边形ABCD中,AB∥DC,AD∥BC, 在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是____________.
4.如图,在 ABCD中, ∠ACB=90°,过点 D 作DE⊥BC 交 BC 的延长线于点E. 求证:四边形ACED 是矩形.
5.如图,已知菱形ABCD的对角线AC,BD 交于点O,∥∥求证:四边形 OCED 是矩形.
纠易错 对矩形的判定方法理解错误导致出错
6.在一组对边平行的四边形中,下列条件中,可判定这个四边形是矩形的是( )
A.另一组对边相等,对角线相等 B.另一组对边相等,对角线互相垂直
C.另一组对边平行,对角线相等 D.另一组对边平行,对角线互相垂直
提 升 练
7.在四边形ABCD中, ∥下列条件能使四边形 ABCD 为矩形的是( )
A. AB∥CD
8.要检验一个四边形的桌面是否为矩形,可行的测量方案是( )
A.测量两条对角线是否相等
B.度量两个角是否是
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
9.如图,□ABCD的对角线 AC,BD 相交于点O,添加下列条件仍不能判定四边形 ABCD 是矩形的是( )
(第9 题) (第 10题)
10.如图,在四边形 ABCD 中, AD=10 cm,BC=8 cm ,点P从点D出发,以1 cm/s的速度向点 A 运动,点 M 从点 B 同时出发,以相同的速度向点 C 运动,当其中一个动点到达终点时,两个动点同时停止运动.设点P 的运动时间为 t(单位:s),下列结论正确的是( )
A. 当t =4时,四边形ABMP 为矩形 B.当t=5时,四边形CDPM为平行四边形
C.当CD=PM时,t=4 D.当CD=PM 时,t=4 或6
11.如图,点 M 在 CD 的边 AD上,BM = CM. 请从以下三个条件①∠1=∠2;②AM= DM;③∠3 =∠4 中,选择一个合适的条件作为已知条件,使 为矩形.
(1)你添加的条件是___________(填序号).
(2)添加条件后,请证明为矩形.
12.如图, 的对角线AC,BD 交于点 O,E为 OC 的中点,过点 C 作∥交BE的延长线于 F,连接DF.
(1)求证:
(2)当 满足什么条件时,四边形OCFD 为矩形 请说明理由.
13.如图,中,AC,BD 相交于点 O,E,F 分别是 OA,OC 的中点.
(1)求证:BE=DF.
(2)设 当k为何值时,四边形 DEBF 是矩形 请说明理由.
参考答案
1. D
2. A 【点拨】∵四边形ABCD是平行四边形,∴ OA=OC,OB =OD.
∵ BM=DN,∴OB-BM=OD-DN , 即OM = ON,∴ 四边形 AMCN 是平行四边形.
∴四边形AMCN是矩形.
3.∠A=90°(答案不唯一)
4.【证明】∵四边形ABCD为平行四边形,∴AD∥BC, ∴∠DAC=∠ACB =90°.
∵DE⊥BC,∴ ∠E=90°.
又∵∠ACE = 180°-∠ACB = 90°,∴ ∠ACE =∠DAC=∠E=90°,
∴四边形ACED 是矩形.
5.【证明】∵CE∥OD,DE∥OC,∴ 四边形OCED是平行四边形.
∵ 四边形 ABCD 是菱形,∴AC⊥BD,∴∠DOC=90°,∴ OCED是矩形.
点方法 证明四边形是矩形的方法:(1) 如果四边形是平行四边形, 可考虑有一个角是直角或对角线相等;(2) 如果四边形有一个角是直角或对角线相等, 可考虑证明四边形是平行四边形;(3) 证明四边形有3个角是直角.
6. C
点易错 此题易因对矩形的判定方法理解错误而出错.在一组对边平行的前提下, 再找该组对边相等或另一组对边平行即可判定这个四边形为平行四边形, 再结合对角线相等即可判定这个四边形是矩形.
7. C 【点拨】A.∵ AB∥CD,AD∥BC,∴ 四边形ABCD是平行四边形,由AB =CD不能判定四边形ABCD为矩形. B.∵AD=BC,AD∥BC,∴ 四边形ABCD 是平行四边形,由AB=CD不能判定四边形 ABCD为矩形. C.∵AD∥BC,∴∠A +∠B=180°.∵∠A=的长为 AD与 BC 间的距离.∵AB=CD,∴CD⊥BC,∴∠C=∠D=90°,∴四边形ABCD是矩形. D.∵AD∥BC,∴∠A+∠B=180°,∠D+∠C=180°.∵∠A =∠D,∴ ∠B=∠C.∵ AB=CD,∴当AD≠BC 时,四边形ABCD 是等腰梯形.
8. C 【点拨】A.对角线相等的四边形不一定是平行四边形,更不能判定其为矩形;B.两个角是 的四边形不一定是矩形,三个角是 的四边形才是矩形;C.由对角线的交点到四个顶点的距离相等,可知四边形的对角线互相平分且对角线相等,所以可判定是矩形;D.两组对边相等的四边形是平行四边形,不能判定其为矩形.
9. B 【点拨】 ∴□ABCD为矩形;B.∵AB =AD,∴□ABCD 为菱形;C.∵四边形ABCD 是平行四边形,∴OA =OC,OB=OD.∵ OA =OD,∴ AC =BD,∴□ABCD 是矩形;D. ∵四边形 ABCD是平行四边形,∴ ∠ABC=∠ADC. ∵ ∠ABC +∠ADC = 180°,∴ ∠ABC=∠ADC=90°,∴ ABCD为矩形.
10. D 【点拨】∵∠A=∠B=90°,∴AD∥BC.根据题意,得DP=t cm,BM =t cm,∵ AD =10 cm,BC =8cm ,∴AP=(10-t) cm,CM=(8-t) cm.当四边形ABMP为矩形时,AP=BM,即10-t=t,解得t=5,故A 错误;当四边形 CDPM 为平行四边形时,DP =CM,即t=8-t,解得 t=4,故 B 错误;当 PM 时,分两种情况:①四边形CDPM 是平行四边形,此时CM=PD,即8-t=t,解得 t=4;②四边形CDPM 是等腰梯形,过点M作MG⊥AD于点G,过点C 作CH⊥AD于点H,则 GH = CM,AG = BM,GM = HC,∠MGP = ∠CHD = 90°. ∵ PM = CD, ∴ Rt△MGP≌Rt△CHD(HL),∴GP = HD,∴ AG= 又∵ BM=tcm,∴t=6.综上,当CD=PM 时,t =4 或6,故C 错误,D正确.
11.(1)① (2)【证明】∵ 四边形ABCD是平行四边形,
∴ AB∥DC,AB = DC,∴ ∠A +∠D =180°.
在△ABM 和△DCM 中,
为矩形.
【点拨】 本题答案不唯一.
(1)【证明】∵ CF∥BD,∴∠CFE=∠OBE.∵ E为OC 的中点,
在 和 中,
(2)【解】当 满足AD=CD时,四边形OCFD为矩形.理由如下:
∵△FCE≌△BOE,∴ CF=OB.
∵四边形ABCD 是平行四边形, OD.∴CF=OD.
又∵CF∥BD,∴四边形OCFD为平行四边形.
∴∠COD=90°.∴ 四边形OCFD 为矩形.
13.(1)【证明】∵ 四边形ABCD是平行四边形, ∴BO=OD,AO=OC.
∵E,F 分别为AO,OC 的中点,
∴ 四边形DEBF 是平行四边形,
(2)【解】当 时,四边形DEBF 是矩形.理由如下:
.
∵四边形DEBF 是平行四边形.∴四边形DEBF 是矩形.
∴ 当 时,四边形DEBF 是矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
