6.2.3 矩形的性质与判定的应用同步练习(含答案)
文档属性
| 名称 | 6.2.3 矩形的性质与判定的应用同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 08:47:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
2 矩形的性质与判定
第3课时 矩形的性质与判定的应用
基 础 练
练点 矩形的性质与判定的应用
1.下列说法中正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相垂直的四边形是菱形
C.平行四边形的对角线平分一组对角 D.矩形的对角线相等且互相平分
2.如图,AC 是矩形ABCD的对角线,分别以点A,C 为圆心,以大于 的长为半径画弧,两弧交于点E,F,直线EF 交 AD 于点M,交 BC 于点 N,若 ,则边 AB 的长为( )
A.6 B.10
(第2题) (第3 题)
3.如图,矩形ABCD 的对角线AC,BD交于点O, 2,则
提 升 练
4.如图,矩形ABCD中,点 E 在BC 边上, 于点 F,若 AB=3,则线段AF 的长为( )
B.4
(第4题) (第4题)
5.如图,矩形ABCD中, 5, 点P在对角线 BD上,且 连接AP 并延长,交 DC 的延长线于点 Q,连接BQ,则BQ的长为__________.
6.【新题型】如图,四边形 ABCD 是个活动框架,对角线 AC,BD 是两根皮筋. 如果拉动这个框架(BC 位置不变)得到矩形. 和 相交于点 O. 连接. 如果四边形为菱形,则
(第6题) (第7题)
7.如图,在 中, , D 是 AB上一点, 于点 E,. 于点 F,连接EF,则EF的最小值为__________ cm.
8.如图,四边形ABCD 是平行四边形,过点 D 作于点E,点 F 在边 CD上, 连接AF , BF.
(1)求证:四边形 BFDE 是矩形.
(2)若 AF 是 的平分线,且 8,求 DC 的长.
9.如图,在 中, ,点D 为 AB 边上任意一点(不与点 A,B重合),过点 D 作 ∥∥分别交AC,BC 于点E,F,连接EF.
(1)求证:四边形 ECFD是矩形.
(2)若 求点 C 到 EF的距离.
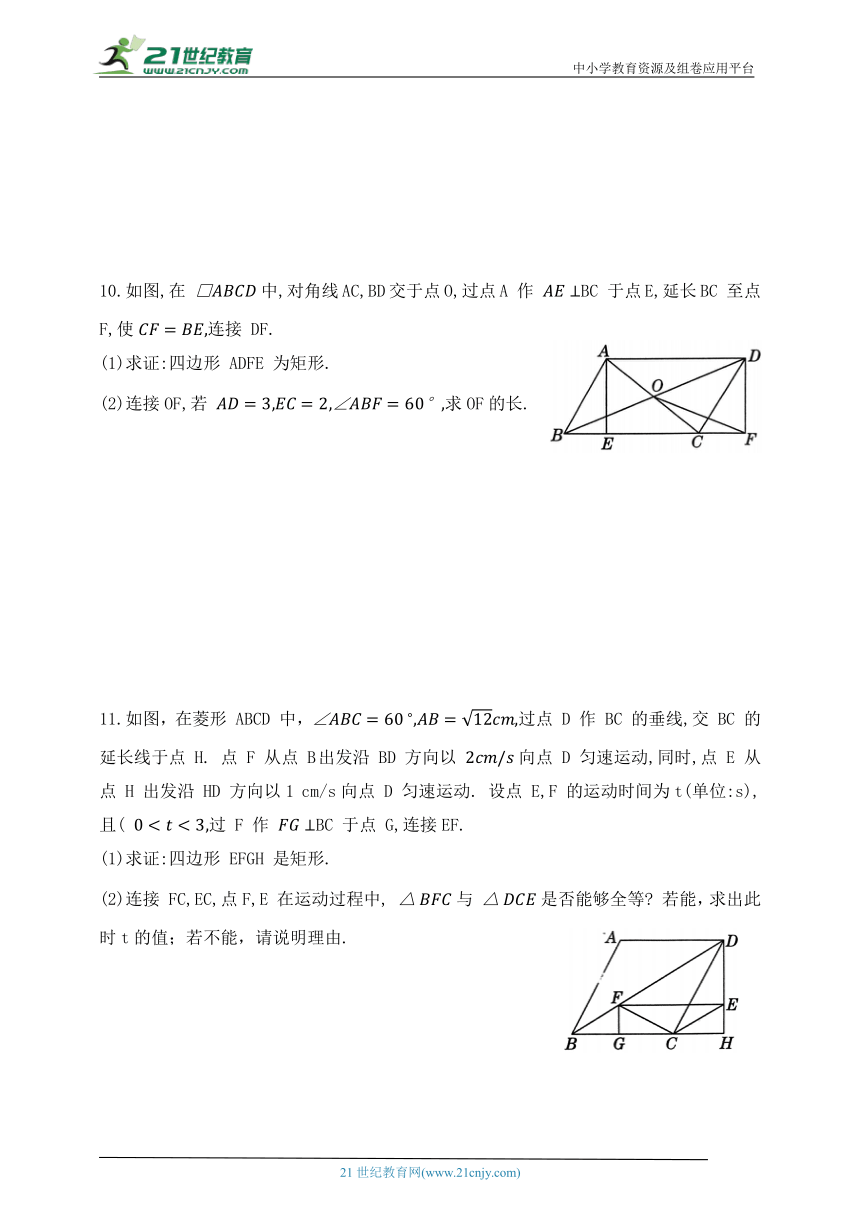
10.如图,在 中,对角线AC,BD交于点O,过点A 作 BC 于点E,延长BC 至点 F,使连接 DF.
(1)求证:四边形 ADFE 为矩形.
(2)连接OF,若 求OF的长.
11.如图,在菱形 ABCD 中,过点 D 作 BC 的垂线,交 BC 的延长线于点 H. 点 F 从点 B出发沿 BD 方向以 向点 D 匀速运动,同时,点 E 从点 H 出发沿 HD 方向以1 cm/s向点 D 匀速运动. 设点 E,F 的运动时间为t(单位:s),且( 过 F 作 BC 于点 G,连接EF.
(1)求证:四边形 EFGH 是矩形.
(2)连接 FC,EC,点F,E 在运动过程中, 与 是否能够全等 若能,求出此时t的值;若不能,请说明理由.
参考答案
1. D
2. D 【点拨】连接CM,由题意知EF 是线段AC 的垂直平分线,
∵四边形ABCD为矩形,
【点拨】∵四边形ABCD为矩形,.
为等边三角形.
在 中,
4. B 【点拨】连接 DE,∵ 四边形ABCD是矩形, ∥
∠DEC,∴∠FED=∠ADE,∴ AE=AD.∵AD=BC,∴ BE=BC-EC =AE-EC.设 AE 为 x,
在Rt△ABE中,由勾股定理得
即 解得x=5,∴AE=5,∴AF=AE-EF =5-1=4.
点方法 求矩形中某线段的长, 常用到勾股定理:一是利用勾股定理直接求线段的长;二是利用勾股定理列方程, 通过解方程求线段的长.
5. 【点拨】∵ 矩形ABCD 中,AB=5,AD=12,
∵BP=BA=5,∴PD=BD-BP=8,∠BAP=∠BPA=∠DPQ.
∵AB∥CD,∴ ∠BAP=∠DQP,∴ ∠DPQ=∠DQP,∴ DQ= DP =8.
∵CD= AB,∴ CQ= DQ -CD=DQ-AB=8-5 =3.
∵ BC=AD,∴ 在Rt△BCQ 中,根据勾股定理,得
6.30 【点拨】由题意得
∵四边形 为菱形,∴ ∠OCD'=∠DCD',DD'= CD,∴ CD'=
是等边三角形,60°,∴∠D'CO = 60°.
∵ 四边形. 是矩形,∴∠BCD'=90°,∴∠A'CB=30°.
7.2.4 【点拨】连接 CD.∵∠ACB=90°,AC =3cm, BC=4 cm,∴
∵DE⊥AC, DF⊥BC,∠ACB =90°,∴ 四边形 CFDE 是矩形, ∴ EF=CD.
由垂线段最短可得CD⊥AB 时,线段CD的长最小,即 EF的长最小,
此时 即 解得CD=2.4 cm,
∴ EF的最小值为2.4 cm.
8.(1)【证明】∵ 四边形ABCD 是平行四边形,∴AB∥DC,AB=DC.
∵CF=AE,∴AB-AE = DC- CF,即BE=FD. ∴ 四边形BFDE 是平行四边形.
∵DE⊥AB,∴∠DEB=90°.∴四边形BFDE 是矩形.
(2)【解】∵ 四边形BFDE 是矩形,∴∠BFC=90°.∵ 四边形 ABCD是平行四边形,∴ AD=BC=10.
∵ AF 是∠DAB 的平分线,∴∠DAF=∠BAF.
∵AB∥DC,∴∠DFA=∠FAB.∴∠DAF=∠DFA.
∴AD=FD=10,∴ DC=DF +FC=10+6=16.
9.(1)【证明】∵ FD∥CA,BC∥DE,∴四边形ECFD为平行四边形.
又∵ ∠C =90°,∴四边形 ECFD 为矩形.
(2)【解】过点 C作 CH⊥EF 于 H,
在 Rt△ECF 中,
∴点C 到 EF 的距离为
10.(1)【证明】∵四边形ABCD是平行四边形, ∴AB∥DC 且AB=DC,∴ ∠ABE=∠DCF.
∵AE⊥BC,∴∠AEB =90°.
在△ABE和△DCF中,
∴AE=DF,∠AEB=∠DFC=90°,∴AE∥DF,∴四边形 ADFE 是平行四边形.
又∵ ∠DFC = 90°,∴平行四边形ADFE是矩形.
(2)【解】∵四边形 ABCD 是平行四边形,
∴ BC=AD=3,CD=AB,OB=OD,∴ CF=BE=BC-EC=1,∴BF= BC + CF =4.
在 Rt△ABE 中,∠ABE=60°,∠AEB=90°,∴∠BAE =90°-∠ABE =30°,
11.(1)【证明】∵ EH⊥BC,FG⊥BC,∴EH∥FG, ∠FGH=∠BGF=90°.
由题意知BF=2t cm,EH=t cm,
∵在菱形ABCD中,∠ABC=60°,∴∠CBD=
∴四边形EFGH是平行四边形.
∵∠FGH=90°,∴ 四边形 EFGH 是矩形.
(2)【解】△BFC 与△DCE 能够全等.
∵ 四边形ABCD是菱形,∴∠ADC=∠ABC=60°,CD=BC=∥
∠DCH=∠ABC =60°.
∵ DH⊥BC,∴ ∠H =90°,∴∠CDH=90°-60°=30°.∴∠CDH=∠CBF.
在Rt△CDH 中,
由题意知BF =2tcm,EH=t cm,∴ DE =(3-t) cm,
∴ 当 BF = DE 时,△BFC≌ 解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
2 矩形的性质与判定
第3课时 矩形的性质与判定的应用
基 础 练
练点 矩形的性质与判定的应用
1.下列说法中正确的是( )
A.对角线相等的四边形是矩形 B.对角线互相垂直的四边形是菱形
C.平行四边形的对角线平分一组对角 D.矩形的对角线相等且互相平分
2.如图,AC 是矩形ABCD的对角线,分别以点A,C 为圆心,以大于 的长为半径画弧,两弧交于点E,F,直线EF 交 AD 于点M,交 BC 于点 N,若 ,则边 AB 的长为( )
A.6 B.10
(第2题) (第3 题)
3.如图,矩形ABCD 的对角线AC,BD交于点O, 2,则
提 升 练
4.如图,矩形ABCD中,点 E 在BC 边上, 于点 F,若 AB=3,则线段AF 的长为( )
B.4
(第4题) (第4题)
5.如图,矩形ABCD中, 5, 点P在对角线 BD上,且 连接AP 并延长,交 DC 的延长线于点 Q,连接BQ,则BQ的长为__________.
6.【新题型】如图,四边形 ABCD 是个活动框架,对角线 AC,BD 是两根皮筋. 如果拉动这个框架(BC 位置不变)得到矩形. 和 相交于点 O. 连接. 如果四边形为菱形,则
(第6题) (第7题)
7.如图,在 中, , D 是 AB上一点, 于点 E,. 于点 F,连接EF,则EF的最小值为__________ cm.
8.如图,四边形ABCD 是平行四边形,过点 D 作于点E,点 F 在边 CD上, 连接AF , BF.
(1)求证:四边形 BFDE 是矩形.
(2)若 AF 是 的平分线,且 8,求 DC 的长.
9.如图,在 中, ,点D 为 AB 边上任意一点(不与点 A,B重合),过点 D 作 ∥∥分别交AC,BC 于点E,F,连接EF.
(1)求证:四边形 ECFD是矩形.
(2)若 求点 C 到 EF的距离.
10.如图,在 中,对角线AC,BD交于点O,过点A 作 BC 于点E,延长BC 至点 F,使连接 DF.
(1)求证:四边形 ADFE 为矩形.
(2)连接OF,若 求OF的长.
11.如图,在菱形 ABCD 中,过点 D 作 BC 的垂线,交 BC 的延长线于点 H. 点 F 从点 B出发沿 BD 方向以 向点 D 匀速运动,同时,点 E 从点 H 出发沿 HD 方向以1 cm/s向点 D 匀速运动. 设点 E,F 的运动时间为t(单位:s),且( 过 F 作 BC 于点 G,连接EF.
(1)求证:四边形 EFGH 是矩形.
(2)连接 FC,EC,点F,E 在运动过程中, 与 是否能够全等 若能,求出此时t的值;若不能,请说明理由.
参考答案
1. D
2. D 【点拨】连接CM,由题意知EF 是线段AC 的垂直平分线,
∵四边形ABCD为矩形,
【点拨】∵四边形ABCD为矩形,.
为等边三角形.
在 中,
4. B 【点拨】连接 DE,∵ 四边形ABCD是矩形, ∥
∠DEC,∴∠FED=∠ADE,∴ AE=AD.∵AD=BC,∴ BE=BC-EC =AE-EC.设 AE 为 x,
在Rt△ABE中,由勾股定理得
即 解得x=5,∴AE=5,∴AF=AE-EF =5-1=4.
点方法 求矩形中某线段的长, 常用到勾股定理:一是利用勾股定理直接求线段的长;二是利用勾股定理列方程, 通过解方程求线段的长.
5. 【点拨】∵ 矩形ABCD 中,AB=5,AD=12,
∵BP=BA=5,∴PD=BD-BP=8,∠BAP=∠BPA=∠DPQ.
∵AB∥CD,∴ ∠BAP=∠DQP,∴ ∠DPQ=∠DQP,∴ DQ= DP =8.
∵CD= AB,∴ CQ= DQ -CD=DQ-AB=8-5 =3.
∵ BC=AD,∴ 在Rt△BCQ 中,根据勾股定理,得
6.30 【点拨】由题意得
∵四边形 为菱形,∴ ∠OCD'=∠DCD',DD'= CD,∴ CD'=
是等边三角形,60°,∴∠D'CO = 60°.
∵ 四边形. 是矩形,∴∠BCD'=90°,∴∠A'CB=30°.
7.2.4 【点拨】连接 CD.∵∠ACB=90°,AC =3cm, BC=4 cm,∴
∵DE⊥AC, DF⊥BC,∠ACB =90°,∴ 四边形 CFDE 是矩形, ∴ EF=CD.
由垂线段最短可得CD⊥AB 时,线段CD的长最小,即 EF的长最小,
此时 即 解得CD=2.4 cm,
∴ EF的最小值为2.4 cm.
8.(1)【证明】∵ 四边形ABCD 是平行四边形,∴AB∥DC,AB=DC.
∵CF=AE,∴AB-AE = DC- CF,即BE=FD. ∴ 四边形BFDE 是平行四边形.
∵DE⊥AB,∴∠DEB=90°.∴四边形BFDE 是矩形.
(2)【解】∵ 四边形BFDE 是矩形,∴∠BFC=90°.∵ 四边形 ABCD是平行四边形,∴ AD=BC=10.
∵ AF 是∠DAB 的平分线,∴∠DAF=∠BAF.
∵AB∥DC,∴∠DFA=∠FAB.∴∠DAF=∠DFA.
∴AD=FD=10,∴ DC=DF +FC=10+6=16.
9.(1)【证明】∵ FD∥CA,BC∥DE,∴四边形ECFD为平行四边形.
又∵ ∠C =90°,∴四边形 ECFD 为矩形.
(2)【解】过点 C作 CH⊥EF 于 H,
在 Rt△ECF 中,
∴点C 到 EF 的距离为
10.(1)【证明】∵四边形ABCD是平行四边形, ∴AB∥DC 且AB=DC,∴ ∠ABE=∠DCF.
∵AE⊥BC,∴∠AEB =90°.
在△ABE和△DCF中,
∴AE=DF,∠AEB=∠DFC=90°,∴AE∥DF,∴四边形 ADFE 是平行四边形.
又∵ ∠DFC = 90°,∴平行四边形ADFE是矩形.
(2)【解】∵四边形 ABCD 是平行四边形,
∴ BC=AD=3,CD=AB,OB=OD,∴ CF=BE=BC-EC=1,∴BF= BC + CF =4.
在 Rt△ABE 中,∠ABE=60°,∠AEB=90°,∴∠BAE =90°-∠ABE =30°,
11.(1)【证明】∵ EH⊥BC,FG⊥BC,∴EH∥FG, ∠FGH=∠BGF=90°.
由题意知BF=2t cm,EH=t cm,
∵在菱形ABCD中,∠ABC=60°,∴∠CBD=
∴四边形EFGH是平行四边形.
∵∠FGH=90°,∴ 四边形 EFGH 是矩形.
(2)【解】△BFC 与△DCE 能够全等.
∵ 四边形ABCD是菱形,∴∠ADC=∠ABC=60°,CD=BC=∥
∠DCH=∠ABC =60°.
∵ DH⊥BC,∴ ∠H =90°,∴∠CDH=90°-60°=30°.∴∠CDH=∠CBF.
在Rt△CDH 中,
由题意知BF =2tcm,EH=t cm,∴ DE =(3-t) cm,
∴ 当 BF = DE 时,△BFC≌ 解得
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
