同步课时精练(三)1.3洛仑兹力(后附解析)
文档属性
| 名称 | 同步课时精练(三)1.3洛仑兹力(后附解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-29 21:40:45 | ||
图片预览




文档简介
同步课时精练(三)1.3 洛仑兹力(后附解析)
一、单选题
1.如图所示,带正电的粒子以水平速度v射入方向竖直向上的匀强磁场时,粒子所受洛伦兹力的方向( )
A.水平向左 B.水平向右
C.竖直向上 D.垂直纸面向外
2.如图所示,把一直导线平行地放在小磁针的正上方附近,当导线中有电流通过时,小磁针会发生偏转。发现这个实验现象的物理学家是( )
A.法拉第 B.安培 C.奥斯特 D.洛伦兹
3.如图所示,在圆形区域内有方向垂直向里的匀强磁场,有一束速率各不相同的质子自A点沿半径方向射入磁场,这些质子在磁场中( )
A.速度越大的,运动时间越长
B.运动时间越长的,其轨迹越长
C.速度越大的,速度的偏转角越小
D.所有质子在磁场中的运动时间相同
4.如图,边长为L的正方形abcd内存在匀强磁场,磁感应强度大小为B,方向垂直于纸面(abcd所在平面)向外。ab边中点有一粒子源O,可向磁场内沿垂直于ab边的方向发射相同的带电粒子(发射速度不相同),带电粒子电荷量为q、质量为m,重力不计。则从b、c两点射出的粒子的速度大小分别为( )
A.从b点射出的粒子的速度大小为
B.从b点射出的粒子的速度大小为
C.从c点射出的粒子的速度大小为
D.从c点射出的粒子的速度大小为
5.在如下匀强电场和匀强磁场共存的区域内,电子可能沿x轴正方向做匀速直线运动的是( )
A. B.
C. D.
6.如图所示,两个初速度大小不同的相同粒子a和b,从O点沿垂直磁场方向进入匀强磁场,其中b粒子速度方向与屏OP垂直,α粒子速度方向与b粒子速度方向夹角θ=45°.两粒子最后均打到屏上同一点Q上,不计重力.下列说法正确的是( )
A.a、b粒子带负电
B.a、b两粒子在磁场中飞行速度之比为∶1
C.a、b两粒子在磁场中飞行的周期之比为2∶3
D.a、b两粒子在磁场中飞行的时间之比为1∶1
7.如图,正方形PNMQ的边长为L,圆心在M,半径也为L的圆形区域MQN 内有垂直于圆面向里、磁感应强度大小为B的匀强磁场,K是圆弧的中点,G是QM边的中点。一群质量为m、电荷量为q的带正电粒子(不计重力),以相同的速度沿既垂直于QM也垂直于磁场的方向从QM边射入磁场。关于从K点离开磁场的粒子,下列说法正确的是( )
A.它是从G点射入的
B.它是从QG之间的某一点射入的
C.它离开磁场后将经过P点
D.它离开磁场后将从P点下方穿过PQ边
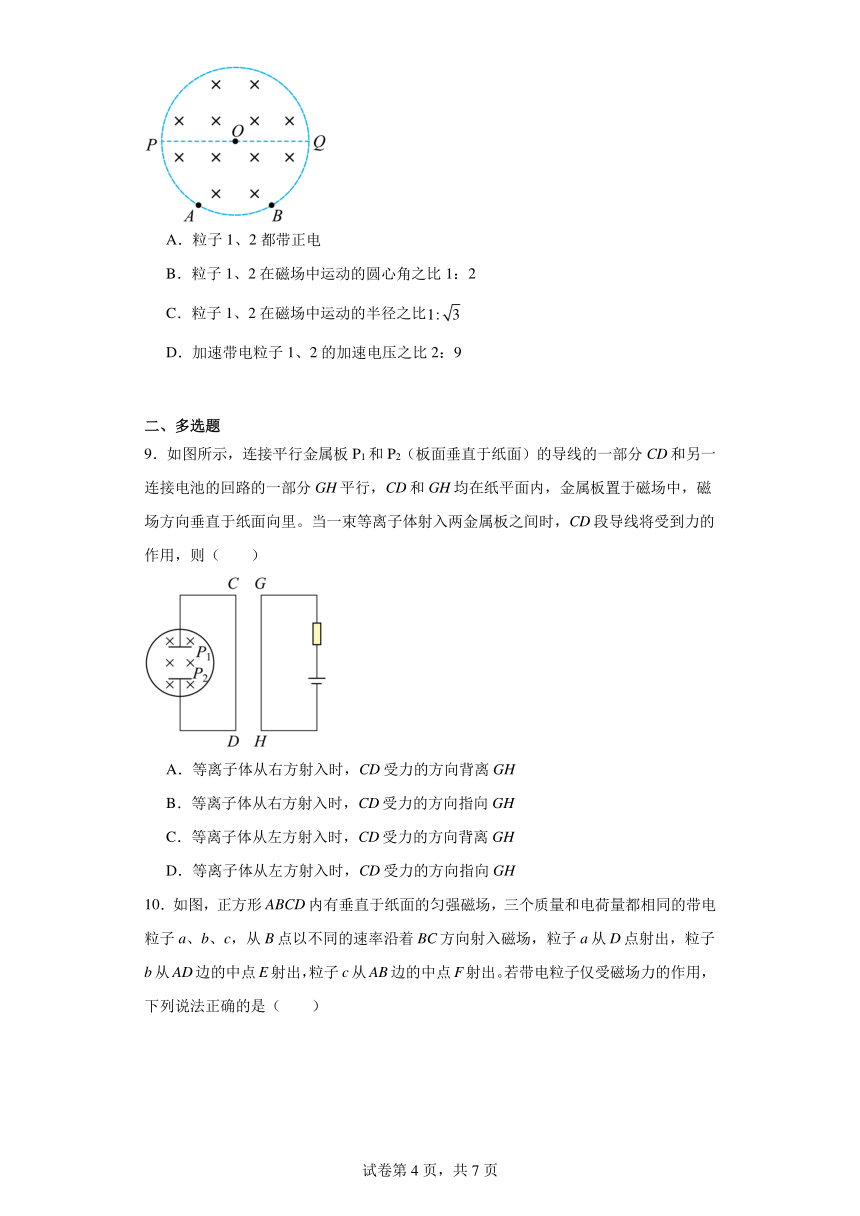
8.如图所示,圆形区域内存在垂直纸面向里的匀强磁场,将两个带电粒子1、2从静止开始分别经不同电场加速后从P点沿直径PQ方向射入磁场,发现粒子1、2分别从A、B两点沿半径方向射出磁场,且它们在磁场中运动的时间相等,A、B两点恰好将半圆三等分,不考虑带电粒子的重力和粒子间的相互作用,下列说法正确的是( )
A.粒子1、2都带正电
B.粒子1、2在磁场中运动的圆心角之比1:2
C.粒子1、2在磁场中运动的半径之比
D.加速带电粒子1、2的加速电压之比2:9
二、多选题
9.如图所示,连接平行金属板P1和P2(板面垂直于纸面)的导线的一部分CD和另一连接电池的回路的一部分GH平行,CD和GH均在纸平面内,金属板置于磁场中,磁场方向垂直于纸面向里。当一束等离子体射入两金属板之间时,CD段导线将受到力的作用,则( )
A.等离子体从右方射入时,CD受力的方向背离GH
B.等离子体从右方射入时,CD受力的方向指向GH
C.等离子体从左方射入时,CD受力的方向背离GH
D.等离子体从左方射入时,CD受力的方向指向GH
10.如图,正方形ABCD内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,从B点以不同的速率沿着BC方向射入磁场,粒子a从D点射出,粒子b从AD边的中点E射出,粒子c从AB边的中点F射出。若带电粒子仅受磁场力的作用,下列说法正确的是( )
A.a粒子的速率是b粒子速率的两倍
B.在磁场中运动的时间,c是a的两倍
C.在磁场中运动的弧长,a等于c
D.若c粒子的速率稍微减小,在磁场中的运动时间不变
11.如图所示,边长为L的正方形ABCD内存在垂直于平面向里的匀强磁场,AB、BC、CD边放有挡板,粒子打到挡板上时会被挡板吸收,在BC中点O有一粒子发射源,可以沿着正方形所在平面朝各个方向发射速率为的同种带电粒子,粒子质量为m,电荷量为。已知垂直BC射入的带电粒子恰好从D点射出磁场,不计粒子的重力和粒子间的相互作用,,以下说法正确的是( )
A.磁场的磁感应强度大小为
B.从D点射出磁场的粒子在磁场中运动时间为
C.有粒子打到B点
D.刚好从A点射出磁场的粒子在磁场中运动时间为
12.如图所示,用丝线吊一个质量为m的带电(绝缘)小球处于匀强磁场中,空气阻力不计,当小球分别从等高的A点和B点向最低点O运动且两次经过O点时( )
A.小球的动能相同 B.丝线所受的拉力相同
C.小球所受的洛伦兹力相同 D.小球的向心加速度相同
三、解答题
13.如图所示,—个质量为、电荷量为的带电粒子,在磁感应强度为B的匀强磁场中,以垂直于磁场方向的速度v做匀速圆周运动。
(1)画出粒子此时所受洛伦兹力的方向及运动轨迹示意图;
(2)推导轨道半径公式;
(3)推导运动周期公式。
14.若电子运动的速率,匀强磁场的磁感应强度,请分别计算在如图所示各种情况下运动电子受到的洛伦兹力的大小,并在图中标明或说明洛伦兹力的方向(图中)。
15.如图所示,一足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场。现从矩形区域ad边的中点O处垂直磁场射入一速度方向跟ad边夹角θ=30°、大小为v0的带正电粒子,已知粒子质量为m,电荷量为q,ad边长为L,ab边足够长,粒子重力不计。
(1)求粒子能从ab边上射出磁场的v0大小范围。
(2)问粒子在磁场中运动的最长时间是多少?在这种情况下,粒子v0大小范围。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
解析:根据左手定则,磁感线穿过手心,四指指向正电荷移动方向,此时大拇指指向垂直于纸面向上,正是正电荷在磁场中受到的洛伦兹力方向。
答案:D。
2.C
解析:A.英国科学家法拉第发现了电磁感应,亲手制成了世界上第一台发电机,提出了电磁场及磁感线、电场线的概念;
B.法国科学家安培提出了著名的分子电流假说;
C.丹麦科学家奥斯特发现了电流的磁效应;
D.荷兰物理学家洛仑兹提出了洛伦兹力公式;
答案:C。
3.C
解析:AD.磁场区域半径为R,轨迹圆心角为α,如图所示
由于粒子相同,根据周期公式
可知所有粒子的运动周期相同,粒子在磁场中运动的时间为
而轨迹半径
粒子运动半径
粒子速度v越大的,则r越大,故α越小,t越小,故AD错误;
B.轨迹的长度为
粒子运动时间越长,α越大,根据数学知识可知弧长S越短,故B错误;
C.根据以上分析可知速度越大的,对应的圆心角越小,速度的偏转角越小,故C正确。
答案:C。
4.B
解析:AB.设从b点射出的粒子的速度大小为v1,轨道半径为r1
解得
A错误,B正确;
CD.设从c点射出的粒子的速度大小为v2,轨道半径为r2
对直角三角形,由勾股定理得
解得
故CD错误。
答案:B。
5.A
解析:A.根据左手定则,洛伦兹力向上,电场力向下,可以平衡,故粒子可能做匀速直线运动,故A正确;
B.根据左手定则,电子受到洛伦兹力沿着﹣z方向,电场力也沿着﹣z方向,故不可能做直线运动,故B错误;
C.速度与磁场方向平行,故洛伦兹力为零,电场力向右,粒子向右做加速运动,故C错误;
D.速度与磁场方向平行,故洛伦兹力为零,电场力向右,粒子向右做加速运动,故D错误;
答案:A。
6.B
解析:A.根据题意作出两球运动的轨迹,如图,由左手定则可知,a、b均带正电,故A错误;
B.若设OQ=2R.则a粒子的运动半径为
b粒子的运动半径为R,根据
可知,a、b两粒子在磁场中飞行速度之比为:1,选项B正确;
C.根据
可知,粒子运动的周期相同,选项C错误;
D.因粒子a在磁场中的偏向角为;粒子a在磁场中的偏向角为;两粒子周期相同,可知a、b两粒子在磁场中飞行的时间之比为3:2,选项D错误;
答案:B。
7.C
解析:AB.根据
得
且
则
即带电粒子在磁场中运动的轨迹圆半径为L,若从M点射入,即离开磁场的点在QM中垂线与磁场边连缘线上,若从G点射入,即离开磁场的点过GM中垂线与磁场边缘连线上,而K在两点之间,所以入射点在GM之间,故AB错误;
CD.带电粒子在磁场中运动的轨迹圆半径为L,圆心在QM的延长线上,在K点的速度垂直于圆心与K的连线即的方向指向P点,而离开磁场后做匀速直线运动,所以必过P点,故C正确D错误。
答案:C。
8.D
解析:A.由题知,带电粒子从P点射入后向下偏转,则根据左手定则可知粒子1、2均带负电,故A错误;
B.设磁场的半径为R,粒子1、2在磁场中做圆周运动,画出粒子1、2运动轨迹如图所示
由几何知识可知,粒子做圆周运动转过的圆心角分别是
θ1= 120°,θ2= 60°
则粒子1、2在磁场中运动的圆心角之比为2:1,故B错误;
C.设粒子的运动轨道半径为r1,r2,则有
,
解得
故C错误;
D.设加速带电粒子1、2的加速度分别为和,则有
,
它们在磁场中运动的时间相等,则有
解得
故D正确。
答案:D。
9.AD
解析:AB.电路中的电流的方向从G到H,当等离子体从右方射入时,由左手定则知电容器的下极板带正电,上极板带负电,电流的方向为由D到C,CD中的电流方向与GH中的电流方向相反,两导线相互排斥,CD受到的作用力向左,即背离GH,故A正确B错误;
CD.等离子体从左方射入时,由左手定则知电容器的上极板带正电,下极板带负电,CD中的电流方向为由C到D,CD中的电流方向与GH中的电流方向相同,CD受到的作用力向右,即指向GH,故D正确C错误。
答案:AD。
10.BD
解析:带电粒子的质量和电荷量都相等,分别设为m和q,由洛伦兹力提供向心力得知:则:
v=
找到粒子b的圆心O如图所示,设正方形的边长为d,在△OAE中,
解得:
即
粒子a的半径:
Ra=d
粒子c的半径:
A.粒子a和b的速率之比:
故A错误;
B.带电粒子在磁场中的运动时间:,其中:,由几何关系可知,粒子 c的轨迹圆心角为π,粒子a的轨迹圆心角为 ,而且两个粒子的周期T一样,故在磁场中运动的时间,c是a的两倍,故B正确;
C.由弧长公式l=αr可知,
所以在磁场中运动的弧长,a是c的两倍,故C错误;
D.由洛伦兹力提供向心力可知,轨迹半径粒子c的速率稍微减少,半径减少,在磁场中运动仍然可以从AB边射出,轨迹对应的圆心角仍然为π,运动时间为,其中周期不变,所以c粒子的速率稍微减小,在磁场中的运动时间不变,故D正确。
答案:BD。
11.AD
解析:A.由运动轨迹可得,如图所示
由几何知识
解得
由于
解得
则
故A正确;
B.从D点射出磁场的粒子,由几何关系可知
即
运动时间为
故B错误;
C.由偏转方向可知,不可能有粒子打到B点,故C错误;
D.从A点射出磁场的粒子对应的弦与从D点射出磁场的粒子弦长相等,故经历的时间相等,即
故D正确。
答案:AD。
12.AD
解析:A.带电绝缘小球受到的洛伦兹力和拉力与小球的速度方向时刻垂直,则洛伦兹力和拉力对小球都不做功,只改变速度方向,不改变速度大小,只有重力做功,故当小球两次经过O点时速度大小相等,动能相同,故A正确;
BC.小球分别从A点和B点向最低点O运动,两次经过O点时速度大小相同、方向相反,由,则洛伦兹力大小相等,由左手定则可知小球两次经过O点时洛伦兹力方向相反。若从A到O点时洛伦兹力向上,则从B点到O时洛伦兹力方向向下,由牛顿第二定律有,从A到O点
解得
从B到O点
解得
故细线所受的拉力大小不同,故BC错误;
D.由
两次经过O点时速度大小相同,可知小球的向心加速度大小相同,方向都竖直向上指向悬点,故D正确。
答案:AD。
13.(1) ;(2);(3)。
解析:(1)粒子在磁场中做匀速圆周运动,运动轨迹如图
(2)带电粒子运动过程中所受洛伦兹力
洛伦兹力充当向心力
解得轨道半径
(3)带电粒子运动周期
14.0;;;;;图像见解析
解析:A.运动方向与磁场平行,不受洛伦兹力;
B.运动方向与磁场垂直,洛伦兹力
根据左手定则,洛伦兹力垂直纸面向外;
C.运动方向与磁场垂直,洛伦兹力
根据左手定则,洛伦兹力竖直向下;
D.运动方向与磁场垂直,洛伦兹力
根据左手定则,洛伦兹力垂直运动方向向上;
E.运动方向与磁场方向有夹角,洛伦兹力
根据左手定则,洛伦兹力垂直纸面向外;
15.(1)解析:(1)粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力得
即
若粒子轨迹恰好与ab边相切,其轨迹如图中Ⅰ所示,设圆心为O1,相应速度为v01,轨道半径为r1,由几何知识得
r1+r1sin θ=
解得
r1=,v01=
若粒子轨迹恰好与cd边相切,轨迹如图中Ⅱ所示,设圆心为O2,相应速度为v02,轨道半径为r2,由几何知识得
r2-r2sin θ=
解得
r2=L,v02=
所以粒子能从ab边上射出磁场的速度v0应满足
(2)粒子在磁场中运动的半径r≤r1时,运动时间最长,此时,粒子从ad边射出,射出时速度与ad边夹角为θ,圆弧所对圆心角α为(2π-2θ),粒子在磁场中做圆周运动的周期
则运动时间
则粒子速度
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,带正电的粒子以水平速度v射入方向竖直向上的匀强磁场时,粒子所受洛伦兹力的方向( )
A.水平向左 B.水平向右
C.竖直向上 D.垂直纸面向外
2.如图所示,把一直导线平行地放在小磁针的正上方附近,当导线中有电流通过时,小磁针会发生偏转。发现这个实验现象的物理学家是( )
A.法拉第 B.安培 C.奥斯特 D.洛伦兹
3.如图所示,在圆形区域内有方向垂直向里的匀强磁场,有一束速率各不相同的质子自A点沿半径方向射入磁场,这些质子在磁场中( )
A.速度越大的,运动时间越长
B.运动时间越长的,其轨迹越长
C.速度越大的,速度的偏转角越小
D.所有质子在磁场中的运动时间相同
4.如图,边长为L的正方形abcd内存在匀强磁场,磁感应强度大小为B,方向垂直于纸面(abcd所在平面)向外。ab边中点有一粒子源O,可向磁场内沿垂直于ab边的方向发射相同的带电粒子(发射速度不相同),带电粒子电荷量为q、质量为m,重力不计。则从b、c两点射出的粒子的速度大小分别为( )
A.从b点射出的粒子的速度大小为
B.从b点射出的粒子的速度大小为
C.从c点射出的粒子的速度大小为
D.从c点射出的粒子的速度大小为
5.在如下匀强电场和匀强磁场共存的区域内,电子可能沿x轴正方向做匀速直线运动的是( )
A. B.
C. D.
6.如图所示,两个初速度大小不同的相同粒子a和b,从O点沿垂直磁场方向进入匀强磁场,其中b粒子速度方向与屏OP垂直,α粒子速度方向与b粒子速度方向夹角θ=45°.两粒子最后均打到屏上同一点Q上,不计重力.下列说法正确的是( )
A.a、b粒子带负电
B.a、b两粒子在磁场中飞行速度之比为∶1
C.a、b两粒子在磁场中飞行的周期之比为2∶3
D.a、b两粒子在磁场中飞行的时间之比为1∶1
7.如图,正方形PNMQ的边长为L,圆心在M,半径也为L的圆形区域MQN 内有垂直于圆面向里、磁感应强度大小为B的匀强磁场,K是圆弧的中点,G是QM边的中点。一群质量为m、电荷量为q的带正电粒子(不计重力),以相同的速度沿既垂直于QM也垂直于磁场的方向从QM边射入磁场。关于从K点离开磁场的粒子,下列说法正确的是( )
A.它是从G点射入的
B.它是从QG之间的某一点射入的
C.它离开磁场后将经过P点
D.它离开磁场后将从P点下方穿过PQ边
8.如图所示,圆形区域内存在垂直纸面向里的匀强磁场,将两个带电粒子1、2从静止开始分别经不同电场加速后从P点沿直径PQ方向射入磁场,发现粒子1、2分别从A、B两点沿半径方向射出磁场,且它们在磁场中运动的时间相等,A、B两点恰好将半圆三等分,不考虑带电粒子的重力和粒子间的相互作用,下列说法正确的是( )
A.粒子1、2都带正电
B.粒子1、2在磁场中运动的圆心角之比1:2
C.粒子1、2在磁场中运动的半径之比
D.加速带电粒子1、2的加速电压之比2:9
二、多选题
9.如图所示,连接平行金属板P1和P2(板面垂直于纸面)的导线的一部分CD和另一连接电池的回路的一部分GH平行,CD和GH均在纸平面内,金属板置于磁场中,磁场方向垂直于纸面向里。当一束等离子体射入两金属板之间时,CD段导线将受到力的作用,则( )
A.等离子体从右方射入时,CD受力的方向背离GH
B.等离子体从右方射入时,CD受力的方向指向GH
C.等离子体从左方射入时,CD受力的方向背离GH
D.等离子体从左方射入时,CD受力的方向指向GH
10.如图,正方形ABCD内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,从B点以不同的速率沿着BC方向射入磁场,粒子a从D点射出,粒子b从AD边的中点E射出,粒子c从AB边的中点F射出。若带电粒子仅受磁场力的作用,下列说法正确的是( )
A.a粒子的速率是b粒子速率的两倍
B.在磁场中运动的时间,c是a的两倍
C.在磁场中运动的弧长,a等于c
D.若c粒子的速率稍微减小,在磁场中的运动时间不变
11.如图所示,边长为L的正方形ABCD内存在垂直于平面向里的匀强磁场,AB、BC、CD边放有挡板,粒子打到挡板上时会被挡板吸收,在BC中点O有一粒子发射源,可以沿着正方形所在平面朝各个方向发射速率为的同种带电粒子,粒子质量为m,电荷量为。已知垂直BC射入的带电粒子恰好从D点射出磁场,不计粒子的重力和粒子间的相互作用,,以下说法正确的是( )
A.磁场的磁感应强度大小为
B.从D点射出磁场的粒子在磁场中运动时间为
C.有粒子打到B点
D.刚好从A点射出磁场的粒子在磁场中运动时间为
12.如图所示,用丝线吊一个质量为m的带电(绝缘)小球处于匀强磁场中,空气阻力不计,当小球分别从等高的A点和B点向最低点O运动且两次经过O点时( )
A.小球的动能相同 B.丝线所受的拉力相同
C.小球所受的洛伦兹力相同 D.小球的向心加速度相同
三、解答题
13.如图所示,—个质量为、电荷量为的带电粒子,在磁感应强度为B的匀强磁场中,以垂直于磁场方向的速度v做匀速圆周运动。
(1)画出粒子此时所受洛伦兹力的方向及运动轨迹示意图;
(2)推导轨道半径公式;
(3)推导运动周期公式。
14.若电子运动的速率,匀强磁场的磁感应强度,请分别计算在如图所示各种情况下运动电子受到的洛伦兹力的大小,并在图中标明或说明洛伦兹力的方向(图中)。
15.如图所示,一足够长的矩形区域abcd内充满磁感应强度为B、方向垂直纸面向里的匀强磁场。现从矩形区域ad边的中点O处垂直磁场射入一速度方向跟ad边夹角θ=30°、大小为v0的带正电粒子,已知粒子质量为m,电荷量为q,ad边长为L,ab边足够长,粒子重力不计。
(1)求粒子能从ab边上射出磁场的v0大小范围。
(2)问粒子在磁场中运动的最长时间是多少?在这种情况下,粒子v0大小范围。
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
解析:根据左手定则,磁感线穿过手心,四指指向正电荷移动方向,此时大拇指指向垂直于纸面向上,正是正电荷在磁场中受到的洛伦兹力方向。
答案:D。
2.C
解析:A.英国科学家法拉第发现了电磁感应,亲手制成了世界上第一台发电机,提出了电磁场及磁感线、电场线的概念;
B.法国科学家安培提出了著名的分子电流假说;
C.丹麦科学家奥斯特发现了电流的磁效应;
D.荷兰物理学家洛仑兹提出了洛伦兹力公式;
答案:C。
3.C
解析:AD.磁场区域半径为R,轨迹圆心角为α,如图所示
由于粒子相同,根据周期公式
可知所有粒子的运动周期相同,粒子在磁场中运动的时间为
而轨迹半径
粒子运动半径
粒子速度v越大的,则r越大,故α越小,t越小,故AD错误;
B.轨迹的长度为
粒子运动时间越长,α越大,根据数学知识可知弧长S越短,故B错误;
C.根据以上分析可知速度越大的,对应的圆心角越小,速度的偏转角越小,故C正确。
答案:C。
4.B
解析:AB.设从b点射出的粒子的速度大小为v1,轨道半径为r1
解得
A错误,B正确;
CD.设从c点射出的粒子的速度大小为v2,轨道半径为r2
对直角三角形,由勾股定理得
解得
故CD错误。
答案:B。
5.A
解析:A.根据左手定则,洛伦兹力向上,电场力向下,可以平衡,故粒子可能做匀速直线运动,故A正确;
B.根据左手定则,电子受到洛伦兹力沿着﹣z方向,电场力也沿着﹣z方向,故不可能做直线运动,故B错误;
C.速度与磁场方向平行,故洛伦兹力为零,电场力向右,粒子向右做加速运动,故C错误;
D.速度与磁场方向平行,故洛伦兹力为零,电场力向右,粒子向右做加速运动,故D错误;
答案:A。
6.B
解析:A.根据题意作出两球运动的轨迹,如图,由左手定则可知,a、b均带正电,故A错误;
B.若设OQ=2R.则a粒子的运动半径为
b粒子的运动半径为R,根据
可知,a、b两粒子在磁场中飞行速度之比为:1,选项B正确;
C.根据
可知,粒子运动的周期相同,选项C错误;
D.因粒子a在磁场中的偏向角为;粒子a在磁场中的偏向角为;两粒子周期相同,可知a、b两粒子在磁场中飞行的时间之比为3:2,选项D错误;
答案:B。
7.C
解析:AB.根据
得
且
则
即带电粒子在磁场中运动的轨迹圆半径为L,若从M点射入,即离开磁场的点在QM中垂线与磁场边连缘线上,若从G点射入,即离开磁场的点过GM中垂线与磁场边缘连线上,而K在两点之间,所以入射点在GM之间,故AB错误;
CD.带电粒子在磁场中运动的轨迹圆半径为L,圆心在QM的延长线上,在K点的速度垂直于圆心与K的连线即的方向指向P点,而离开磁场后做匀速直线运动,所以必过P点,故C正确D错误。
答案:C。
8.D
解析:A.由题知,带电粒子从P点射入后向下偏转,则根据左手定则可知粒子1、2均带负电,故A错误;
B.设磁场的半径为R,粒子1、2在磁场中做圆周运动,画出粒子1、2运动轨迹如图所示
由几何知识可知,粒子做圆周运动转过的圆心角分别是
θ1= 120°,θ2= 60°
则粒子1、2在磁场中运动的圆心角之比为2:1,故B错误;
C.设粒子的运动轨道半径为r1,r2,则有
,
解得
故C错误;
D.设加速带电粒子1、2的加速度分别为和,则有
,
它们在磁场中运动的时间相等,则有
解得
故D正确。
答案:D。
9.AD
解析:AB.电路中的电流的方向从G到H,当等离子体从右方射入时,由左手定则知电容器的下极板带正电,上极板带负电,电流的方向为由D到C,CD中的电流方向与GH中的电流方向相反,两导线相互排斥,CD受到的作用力向左,即背离GH,故A正确B错误;
CD.等离子体从左方射入时,由左手定则知电容器的上极板带正电,下极板带负电,CD中的电流方向为由C到D,CD中的电流方向与GH中的电流方向相同,CD受到的作用力向右,即指向GH,故D正确C错误。
答案:AD。
10.BD
解析:带电粒子的质量和电荷量都相等,分别设为m和q,由洛伦兹力提供向心力得知:则:
v=
找到粒子b的圆心O如图所示,设正方形的边长为d,在△OAE中,
解得:
即
粒子a的半径:
Ra=d
粒子c的半径:
A.粒子a和b的速率之比:
故A错误;
B.带电粒子在磁场中的运动时间:,其中:,由几何关系可知,粒子 c的轨迹圆心角为π,粒子a的轨迹圆心角为 ,而且两个粒子的周期T一样,故在磁场中运动的时间,c是a的两倍,故B正确;
C.由弧长公式l=αr可知,
所以在磁场中运动的弧长,a是c的两倍,故C错误;
D.由洛伦兹力提供向心力可知,轨迹半径粒子c的速率稍微减少,半径减少,在磁场中运动仍然可以从AB边射出,轨迹对应的圆心角仍然为π,运动时间为,其中周期不变,所以c粒子的速率稍微减小,在磁场中的运动时间不变,故D正确。
答案:BD。
11.AD
解析:A.由运动轨迹可得,如图所示
由几何知识
解得
由于
解得
则
故A正确;
B.从D点射出磁场的粒子,由几何关系可知
即
运动时间为
故B错误;
C.由偏转方向可知,不可能有粒子打到B点,故C错误;
D.从A点射出磁场的粒子对应的弦与从D点射出磁场的粒子弦长相等,故经历的时间相等,即
故D正确。
答案:AD。
12.AD
解析:A.带电绝缘小球受到的洛伦兹力和拉力与小球的速度方向时刻垂直,则洛伦兹力和拉力对小球都不做功,只改变速度方向,不改变速度大小,只有重力做功,故当小球两次经过O点时速度大小相等,动能相同,故A正确;
BC.小球分别从A点和B点向最低点O运动,两次经过O点时速度大小相同、方向相反,由,则洛伦兹力大小相等,由左手定则可知小球两次经过O点时洛伦兹力方向相反。若从A到O点时洛伦兹力向上,则从B点到O时洛伦兹力方向向下,由牛顿第二定律有,从A到O点
解得
从B到O点
解得
故细线所受的拉力大小不同,故BC错误;
D.由
两次经过O点时速度大小相同,可知小球的向心加速度大小相同,方向都竖直向上指向悬点,故D正确。
答案:AD。
13.(1) ;(2);(3)。
解析:(1)粒子在磁场中做匀速圆周运动,运动轨迹如图
(2)带电粒子运动过程中所受洛伦兹力
洛伦兹力充当向心力
解得轨道半径
(3)带电粒子运动周期
14.0;;;;;图像见解析
解析:A.运动方向与磁场平行,不受洛伦兹力;
B.运动方向与磁场垂直,洛伦兹力
根据左手定则,洛伦兹力垂直纸面向外;
C.运动方向与磁场垂直,洛伦兹力
根据左手定则,洛伦兹力竖直向下;
D.运动方向与磁场垂直,洛伦兹力
根据左手定则,洛伦兹力垂直运动方向向上;
E.运动方向与磁场方向有夹角,洛伦兹力
根据左手定则,洛伦兹力垂直纸面向外;
15.(1)
即
若粒子轨迹恰好与ab边相切,其轨迹如图中Ⅰ所示,设圆心为O1,相应速度为v01,轨道半径为r1,由几何知识得
r1+r1sin θ=
解得
r1=,v01=
若粒子轨迹恰好与cd边相切,轨迹如图中Ⅱ所示,设圆心为O2,相应速度为v02,轨道半径为r2,由几何知识得
r2-r2sin θ=
解得
r2=L,v02=
所以粒子能从ab边上射出磁场的速度v0应满足
(2)粒子在磁场中运动的半径r≤r1时,运动时间最长,此时,粒子从ad边射出,射出时速度与ad边夹角为θ,圆弧所对圆心角α为(2π-2θ),粒子在磁场中做圆周运动的周期
则运动时间
则粒子速度
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 磁场
- 第一节 安培力
- 第二节 安培力的应用
- 第三节 洛伦兹力
- 第四节 洛伦兹力与现代技术
- 第二章 电磁感应
- 第一节 感应电流的方向
- 第二节 法拉第电磁感应定律
- 第三节 电磁感应定律的应用
- 第四节 互感和自感
- 第五节 涡流现象及其应用
- 第三章 交变电流
- 第一节 认识交变电流
- 第二节 描述交变电流的物理量
- 第三节 变压器
- 第四节 远距离输电
- 第四章 电磁震荡与电磁波
- 第一节 电磁振动
- 第二节 麦克斯韦电磁电磁场理论
- 第三节 电磁波的发射、传播和接收
- 第四节 电磁波谱
- 第五章 传感器
- 第一节 传感器及其工作原理
- 第二节 传感器的应用
- 第三节 用传感器制作自动控制装置
- 第四节 利用智能手机中的磁传感器研究磁现象
