勾股定理(4)
图片预览


文档简介
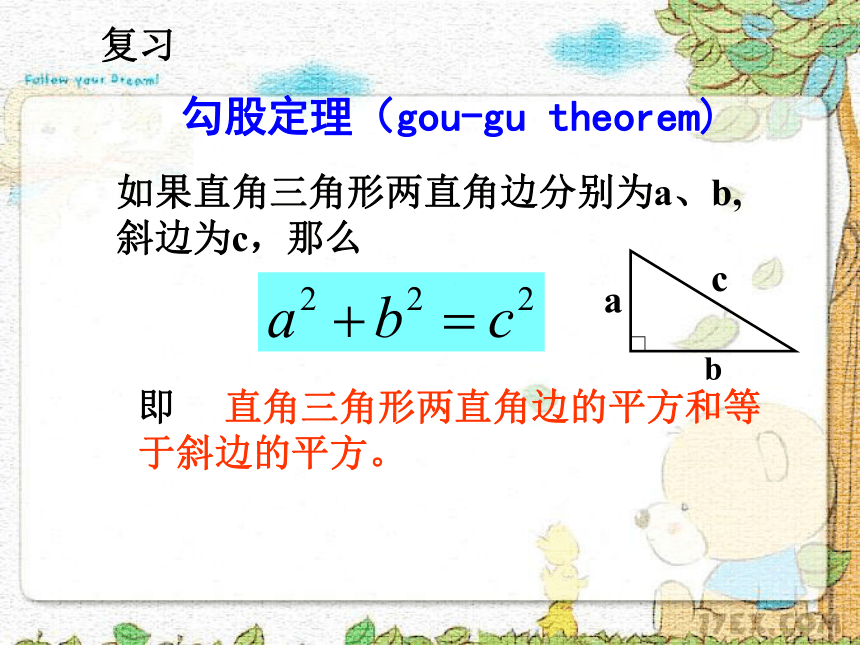
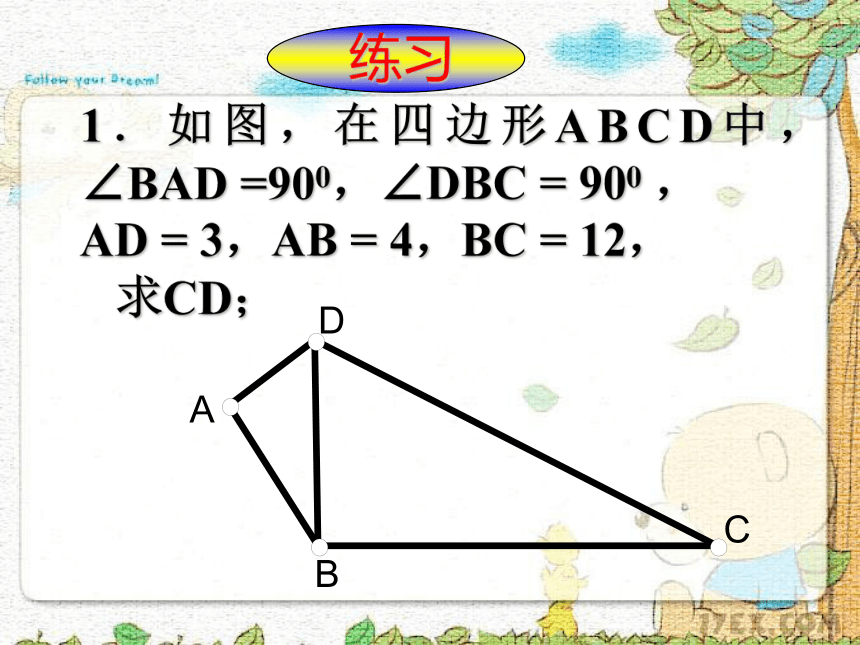
课件14张PPT。塘沽六中初二数学组14.1勾股定理(4)---勾股定理的拓展训练 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。复习1.如图,在四边形ABCD中,∠BAD =900,∠DBC = 900 ,
AD = 3,AB = 4,BC = 12,
求CD;
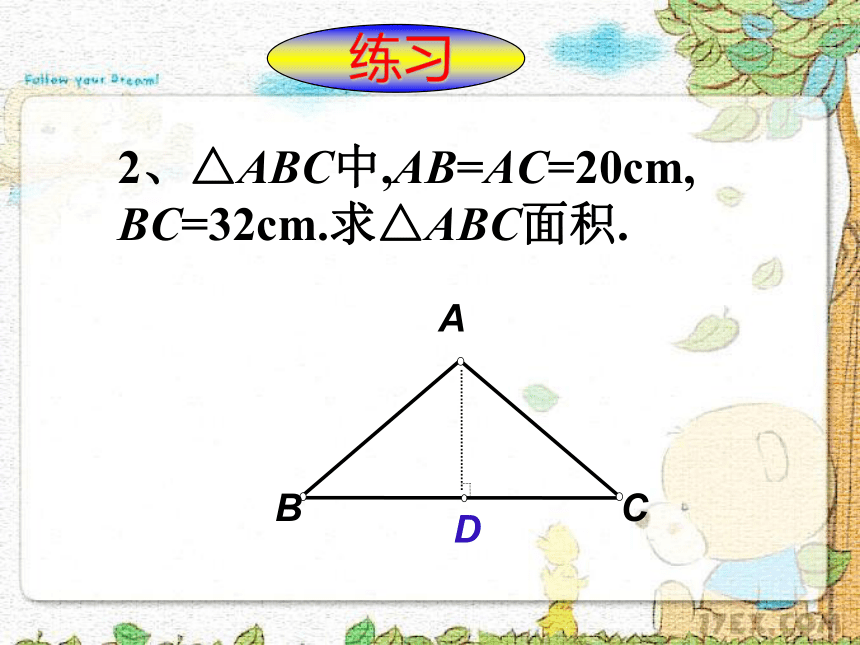
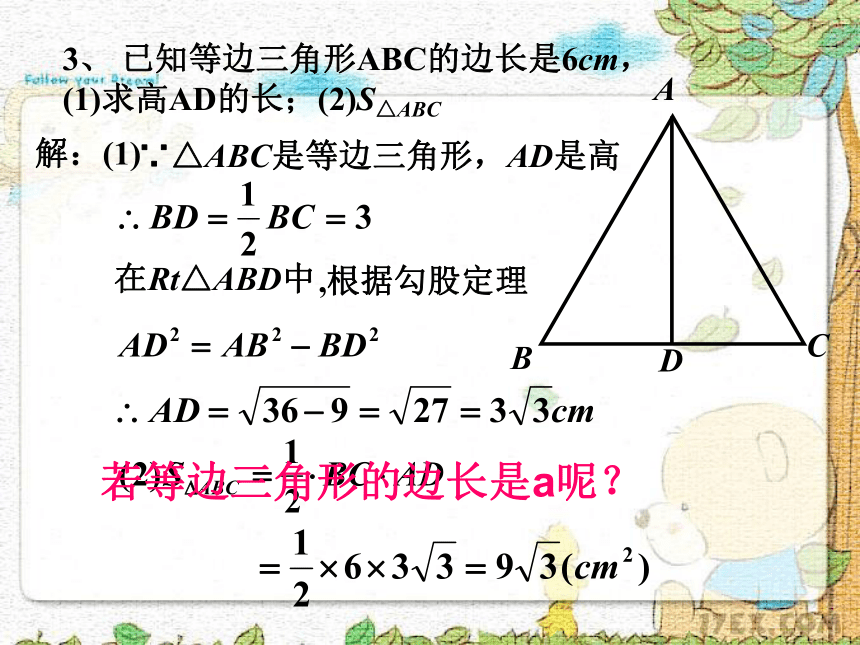
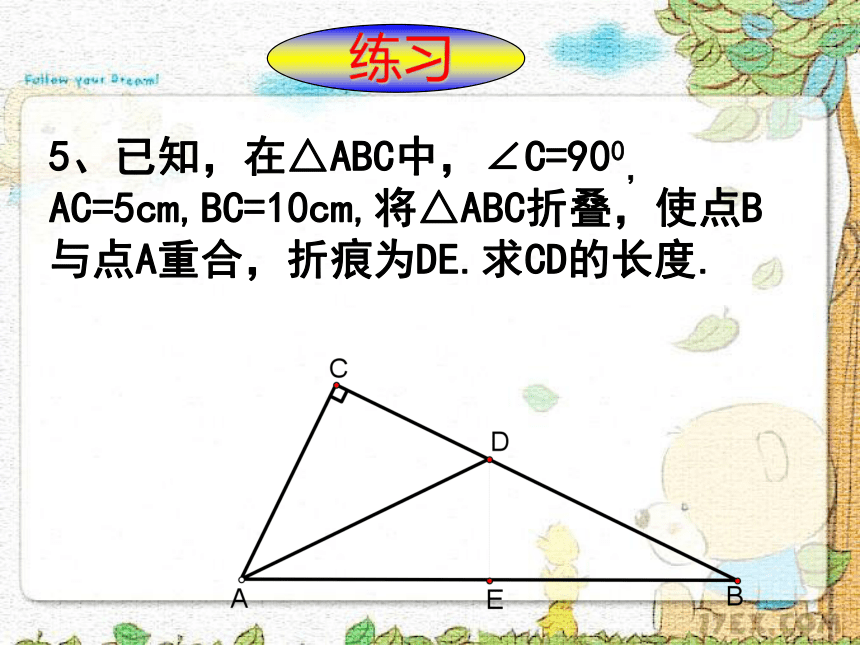
练习 练习3、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理若等边三角形的边长是a呢?4、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=85、已知,在△ABC中,∠C=900,
AC=5cm,BC=10cm,将△ABC折叠,使点B
与点A重合,折痕为DE.求CD的长度. 练习6.如图,在△ABC中,∠ACB=900,AB=50cm,BC=30cm,CD⊥AB于D,求CD的长。提示:利用面积相等的关系 练习7、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 练习8.如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。 练习9、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD 本节课学习了什么内容?你对学习本节课知识有什么体会?谈一谈作业布置1、课本10页: 8、11
2、课堂练习:4页:14
8页:5---14(12题除外)作业布置书:
AD = 3,AB = 4,BC = 12,
求CD;
练习 练习3、 已知等边三角形ABC的边长是6cm,(1)求高AD的长;(2)S△ABC解:(1)∵△ABC是等边三角形,AD是高在Rt△ABD中,根据勾股定理若等边三角形的边长是a呢?4、 如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。解:∵∠ABD=90°,∠DAB=30°在Rt△ABD中,根据勾股定理在Rt△ABC中,又AD=85、已知,在△ABC中,∠C=900,
AC=5cm,BC=10cm,将△ABC折叠,使点B
与点A重合,折痕为DE.求CD的长度. 练习6.如图,在△ABC中,∠ACB=900,AB=50cm,BC=30cm,CD⊥AB于D,求CD的长。提示:利用面积相等的关系 练习7、在等腰△ABC中,AB=AC=13cm ,BC=10cm,求△ABC的面积和AC边上的高。ABCD131310H提示:利用面积相等的关系 练习8.如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积。 练习9、 如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD证明:过A作AE⊥BC于EE∵AB=AC,∴BE=CE在Rt △ADE中,AD2=AE2+DE2在Rt △ABE中,AB2=AE2+BE2∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)= DE2- BE2= (DE+BE)·( DE- BE)= (DE+CE)·( DE- BE)=BD·CD 本节课学习了什么内容?你对学习本节课知识有什么体会?谈一谈作业布置1、课本10页: 8、11
2、课堂练习:4页:14
8页:5---14(12题除外)作业布置书:
