抛物线及其标准方程

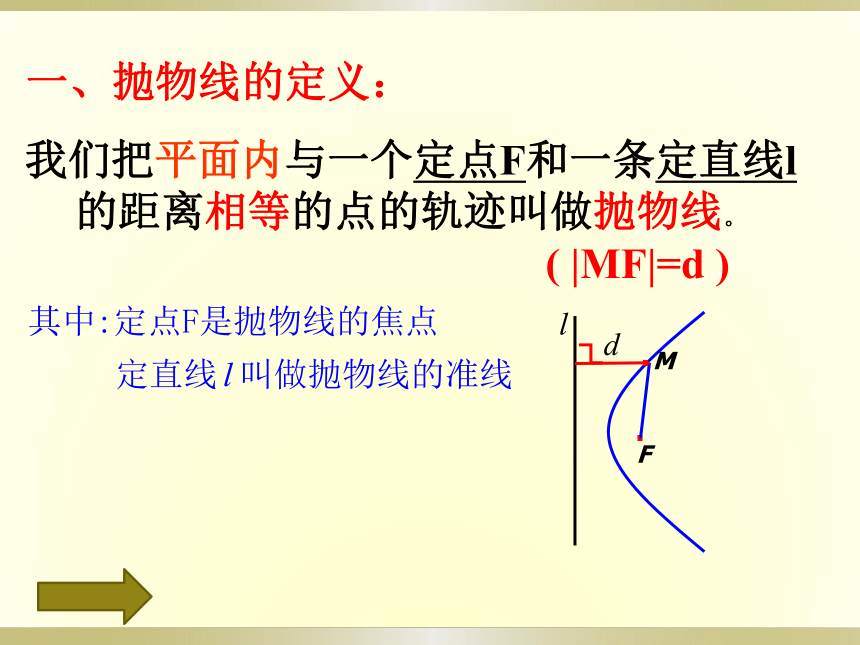
课件24张PPT。喷泉小结：抛物拱形桥2.4.1抛物线及其标准方程（一）返回抛物线的生活实例投篮运动篮球在空中运动的轨迹是抛物线，那么抛物线有怎样的几何特征？一、抛物线的定义：我们把平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线。( |MF|=d ).FM.二、抛物线的标准方程：设|FK|=p(p>0),M(x,y)由抛物线定义知：MF=d22:15:20 把方程 y2 = 2px（p＞0） 叫做抛物线的标准方程而p 的几何意义是: 焦点到准线的距离在学习椭圆和双曲线的时候，由于在坐标平面内的焦点位置不同，导致方程不同。同样抛物线焦点位置不同，方程也会有所不同。二.抛物线的标准方程返回三、抛物线的标准方程▲如何确定抛物线的焦点位置？
抛物线：1.看一次项(X或Y)定焦点
2. 一次项系数正负定开口椭　圆：看分母大小
双曲线：看符号返回22:15:20例1 已知抛物线的标准方程是y2 = 6x，
求它的焦点坐标和准线方程；练习1、求下列抛物线的焦点坐标和准线方程：
（1）y2 = 20x （2）y = 2x2
（3）2y2 +5x =0 （4）x2 +8y =0（5，0）x= -5（0，-2）y=222:15:21例2 已知抛物线的焦点坐标是F（0，-2）
求它的标准方程。
22:15:21变式 根据下列条件写出抛物线的标准方程。 1
4 2. 焦点到准线的距离是2 .y2 =4x、 y2 = -4x、
x2 =4y 或 x2 = -4yy2 =x1. 准线方程是x = － ； 例3：一种卫星接收天线的轴截面如下图所示。卫星波束呈近似平行状态射入轴截面为抛物线的接收天线，经反射聚集到焦点处。已知接收天线的径口（直径）为4.8m，深度为0.5m。建立适当的坐标系，求抛物线的标准方程和焦点坐标。（0.5，2.4）解：如上图，在接收天线的轴截面所在平面内建立直角坐标系，使接收天线的顶点（即抛物线的顶点）与原点重合。 22:15:21解题感悟:求抛物线标准方程的步骤：（1）确定抛物线的形式.（2）求p值（3）写抛物线方程注意:焦点或开口方向不定，则要注意分类讨论结束求过点A（-3，2）的抛物线的
标准方程。巩固提高：返回思考题（选做）：点M与点F(4,0)的距离比它到直线l:x+5=0的距离小1,求点M的轨迹方程.F(4,0)Mx+5=0 解:由已知条件可知,点M与点F的距离等于它到直线x+4=0的距离,根据抛物线的定义,点M的轨迹是以点F(4,0)为焦点的抛物线.
∵p/2=4,
∴p=8.
又因为焦点在轴的正半轴,所以点M的轨迹方程为
y2=16x.X+4=022:15:211、理解抛物线的定义,四种标准方程类型.2、会求不同类型抛物线的焦点坐标、准线方程3、会求抛物线标准方程
小结选做课后作业：高中教学质量监控讲义:抛物线及其标准方程