5.2.2平行线的判定(广东省湛江市霞山区20中)
文档属性
| 名称 | 5.2.2平行线的判定(广东省湛江市霞山区20中) |

|
|
| 格式 | rar | ||
| 文件大小 | 642.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-02 00:00:00 | ||
图片预览



文档简介
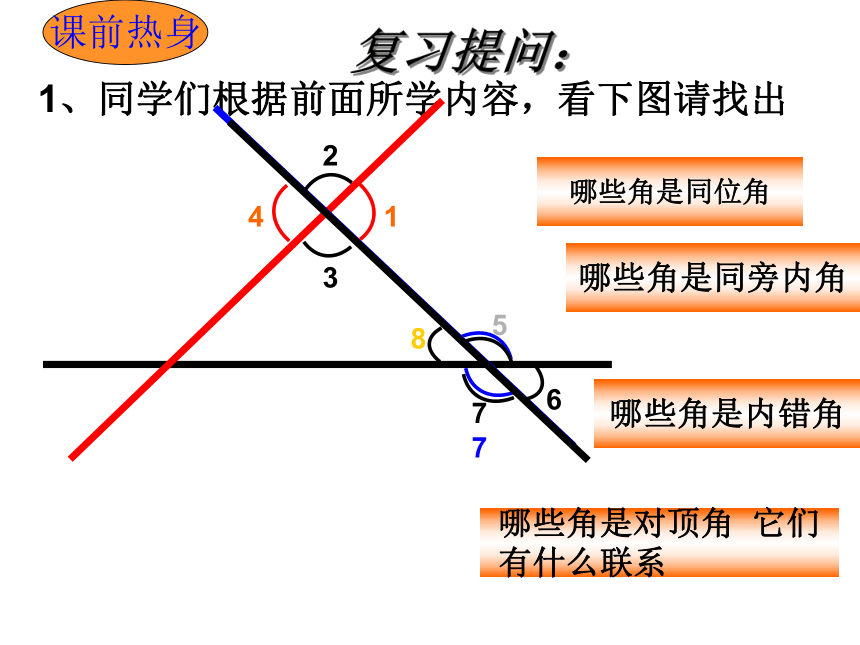
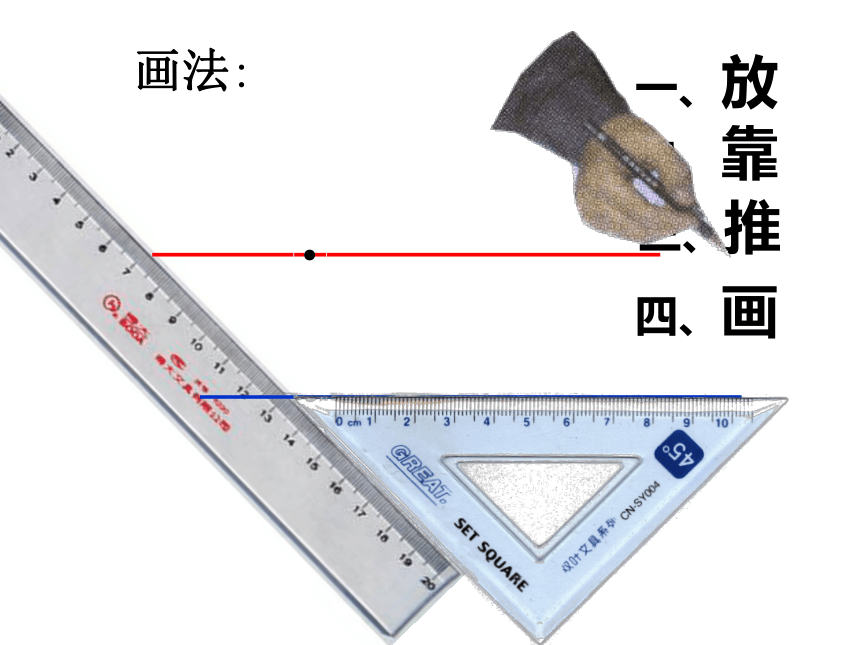
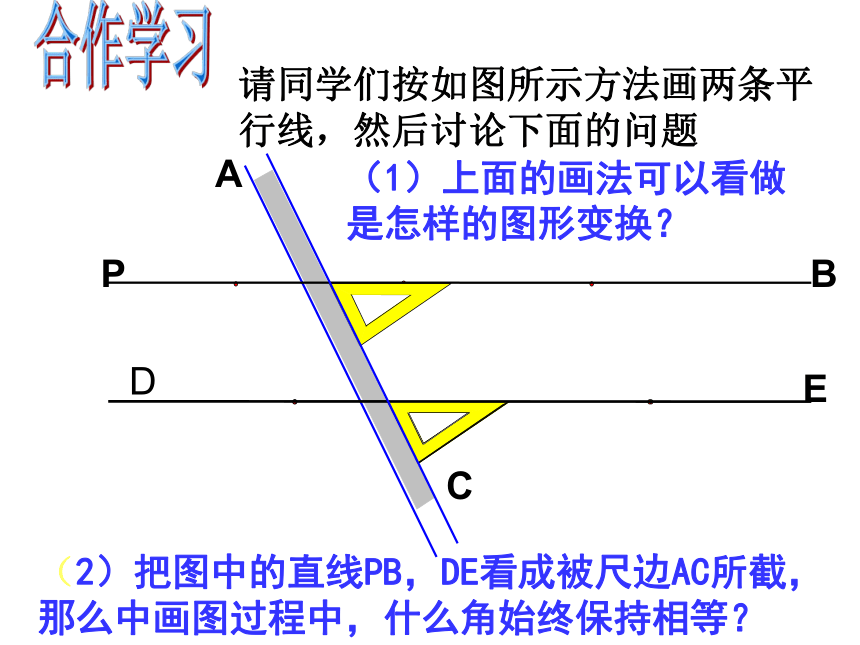
课件29张PPT。5.2.2平行线的判定授课人:沈海尉判断2.与一条直线平行的直线只有一条. 1.两条直线不相交,就叫平行线. 1、同学们根据前面所学内容,看下图请找出哪些角是内错角哪些角是同位角哪些角是同旁内角哪些角是对顶角 它们有什么联系234157786复习提问:课前热身复习提问(2)想一想平面内两条直线的位置关系有几种?(3)怎样过已知直线外一点画已知直线的平行线?一、放二、靠三、推四、画画法:●DABP合作学习请同学们按如图所示方法画两条平行线,然后讨论下面的问题(1)上面的画法可以看做是怎样的图形变换?C(2)把图中的直线PB,DE看成被尺边AC所截,那么中画图过程中,什么角始终保持相等?E平行线的判定定理1 两条直线被第三条直线所截,如果同位角相等,那么这两 条直线平行。简单地说:同位角相等,两直线平行。l1 l2 12符号表示:∵∠1=∠2
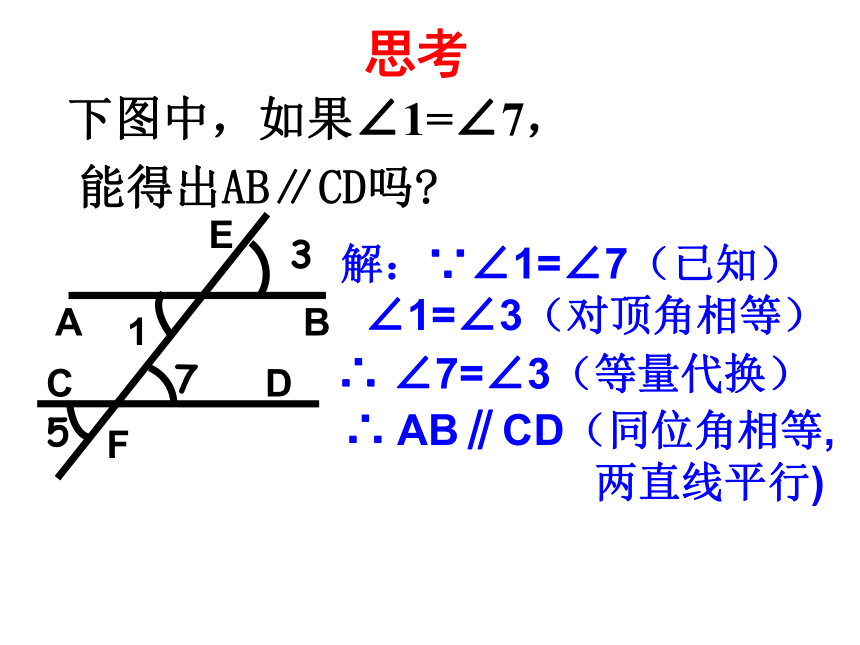
∴l1∥l2 新课讲解下图中,如果∠1=∠7,
能得出AB∥CD吗?思考解:∵∠1=∠7(已知)
∠1=∠3(对顶角相等)
∴ ∠7=∠3(等量代换)∴ AB∥CD(同位角相等,
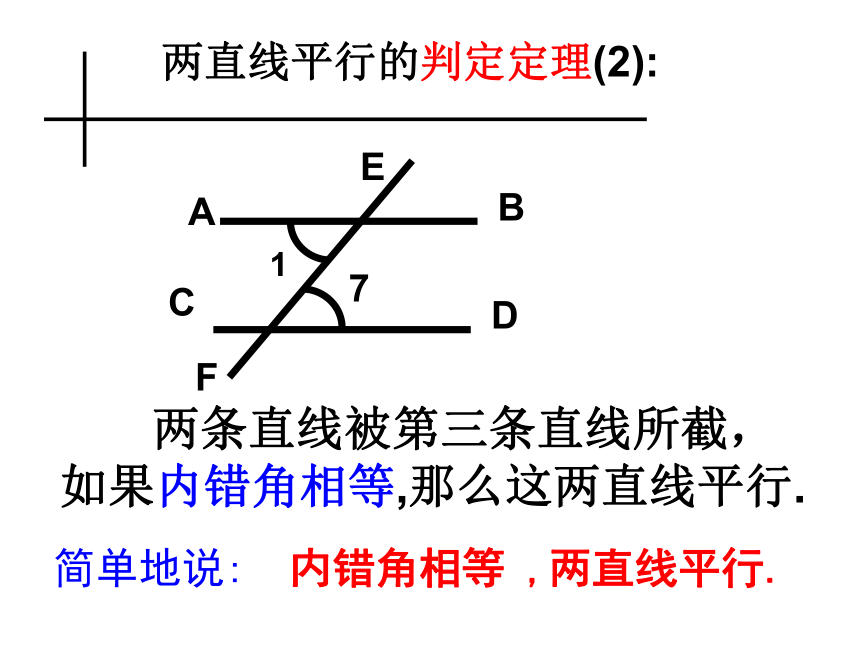
两直线平行)B1ACDF37E5两直线平行的判定定理(2): 两条直线被第三条直线所截,
如果内错角相等,那么这两直线平行.C简单地说: 内错角相等 ,两直线平行.如图:如果?2+ ? 3=180°,那么a//b,为什么?
请写出你的推理过程。平行线的判定定理3
同旁内角互补,两直线平行。推理
格式 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°abc12341.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
6.平行线的定义.
判定两条直线是否平行的方法有:1.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直意义)
∴b∥c(同位角相等,两直线平行)abc12课堂练习 练习:
4.如图, 木工师傅用直尺画出工件边缘的
两条垂线, 这两条垂线平行吗?为什么?ab 解:这两条垂线平行.
∵a、b都垂直于工件边缘
∴ ∠1=∠2 =90°(垂直定义)
∴a∥b(同位角相等,两直线平行)有一块木板,怎样才能知道它上下边缘是否平行?考考你有一块木板,怎样才能知道它上下边缘是否平行?考考你有一块木板,怎样才能知道它上下边缘是否平行?1考考你12有一块木板,怎样才能知道它上下边缘是否平行?考考你12如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?答:AB//CD,AD//BC ∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC快速抢答练习: (1)∵ ∠1=∠2(已知) ∴ ( ) (2)∵ ∠3=∠4(已知) ∴ ( ) ABCD1234ADBC∥∥ABCD内错角相等,两直线平行内错角相等,两直线平行3.某人骑自行车从 A 地出发,沿正东方向前进至 B 处后,右转 150,沿直线向前行驶到C处(如图).这时他想仍按正东方向?请画出他应怎样调整行驶的路线,并说明理由.DE15°能力挑战:(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3 D能力挑战:3、如图,哪些直线平行,哪些直线不平行?能力挑战:2、如图,∠1=∠2,则下列结论正确的是( )(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BCC例1 看图填空 (1) ∵ ∠1=∠E (已知) ∴ ∥ (
) ABCDE123(2) ∵ ∠2=∠D (已知) ∴ ∥ ( ) (3) ∵ ∠ B =∠ 3 (已知) ∴ ∥ ( ) (4) ∵ ∠ A =∠ 2 (已知) ∴ ∥ ( ) ACDE 同位角相等,两直线平行ACDE AB CDABCD内错角相等,两直线平行内错角相等,两直线平行同位角相等,两直线平行例2 已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知) ∴ ∠2=∠C (等量代换) ∴ AC∥FD (同位角相等,两直线平行) FEBCDA21证明:例3 已知:如图,∠DAB被AC平分,
且∠1=∠3,
ABCD123求证:AB∥CD.
∵ ∠DAB被AC平分 (已知) ∴ ∠1=∠2 (角平分线定义) ∵ ∠1=∠3 (已知) ∴ ∠2=∠3 (等量代换) ∴ AB∥CD ( 内错角相等,两直线平行 ) 证明:例4 已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行) FEMNA21BC证明:例一:如图,已知∠BED=∠B+∠D
试说明AB∥CD的理由.
∴l1∥l2 新课讲解下图中,如果∠1=∠7,
能得出AB∥CD吗?思考解:∵∠1=∠7(已知)
∠1=∠3(对顶角相等)
∴ ∠7=∠3(等量代换)∴ AB∥CD(同位角相等,
两直线平行)B1ACDF37E5两直线平行的判定定理(2): 两条直线被第三条直线所截,
如果内错角相等,那么这两直线平行.C简单地说: 内错角相等 ,两直线平行.如图:如果?2+ ? 3=180°,那么a//b,为什么?
请写出你的推理过程。平行线的判定定理3
同旁内角互补,两直线平行。推理
格式 判定两条直线平行的方法同位角内错角同旁内角∠1=∠2∠3=∠2∠2+∠4=180°abc12341.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.如果两条直线都与第三条直线垂直,
那么这两条直线也互相平行.
6.平行线的定义.
判定两条直线是否平行的方法有:1.两条直线垂直于同一条直线,这两条
直线平行吗?为什么?答:垂直于同一条直线的两条直线平行.
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直意义)
∴b∥c(同位角相等,两直线平行)abc12课堂练习 练习:
4.如图, 木工师傅用直尺画出工件边缘的
两条垂线, 这两条垂线平行吗?为什么?ab 解:这两条垂线平行.
∵a、b都垂直于工件边缘
∴ ∠1=∠2 =90°(垂直定义)
∴a∥b(同位角相等,两直线平行)有一块木板,怎样才能知道它上下边缘是否平行?考考你有一块木板,怎样才能知道它上下边缘是否平行?考考你有一块木板,怎样才能知道它上下边缘是否平行?1考考你12有一块木板,怎样才能知道它上下边缘是否平行?考考你12如图:?B= ? D=45°, ? C=135°,
问图中有哪些直线平行?答:AB//CD,AD//BC ∵? B=45°(已知)
? C=135°(已知)
?? B+ ? C=180°
? AB//CD(同旁内角互补,两直线平行)
同理:AD//BC快速抢答练习: (1)∵ ∠1=∠2(已知) ∴ ( ) (2)∵ ∠3=∠4(已知) ∴ ( ) ABCD1234ADBC∥∥ABCD内错角相等,两直线平行内错角相等,两直线平行3.某人骑自行车从 A 地出发,沿正东方向前进至 B 处后,右转 150,沿直线向前行驶到C处(如图).这时他想仍按正东方向?请画出他应怎样调整行驶的路线,并说明理由.DE15°能力挑战:(A)∠2=∠3 (B)∠1=∠4
(C)∠1=∠2 (D)∠1=∠3 D能力挑战:3、如图,哪些直线平行,哪些直线不平行?能力挑战:2、如图,∠1=∠2,则下列结论正确的是( )(A)AD//BC (B)AB//CD
(C)AD//EF (D)EF//BCC例1 看图填空 (1) ∵ ∠1=∠E (已知) ∴ ∥ (
) ABCDE123(2) ∵ ∠2=∠D (已知) ∴ ∥ ( ) (3) ∵ ∠ B =∠ 3 (已知) ∴ ∥ ( ) (4) ∵ ∠ A =∠ 2 (已知) ∴ ∥ ( ) ACDE 同位角相等,两直线平行ACDE AB CDABCD内错角相等,两直线平行内错角相等,两直线平行同位角相等,两直线平行例2 已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知) ∴ ∠2=∠C (等量代换) ∴ AC∥FD (同位角相等,两直线平行) FEBCDA21证明:例3 已知:如图,∠DAB被AC平分,
且∠1=∠3,
ABCD123求证:AB∥CD.
∵ ∠DAB被AC平分 (已知) ∴ ∠1=∠2 (角平分线定义) ∵ ∠1=∠3 (已知) ∴ ∠2=∠3 (等量代换) ∴ AB∥CD ( 内错角相等,两直线平行 ) 证明:例4 已知:如图,∠1=∠C,∠2=∠B,
求证:MN∥EF.
∵ ∠1=∠C (已知) ∴ MN∥BC (内错角相等,两直线平行) ∵ ∠2=∠B (已知) ∴ EF∥BC (同位角相等,两直线平行) ∴ MN∥EF (平行于同一直线的两条直线平行) FEMNA21BC证明:例一:如图,已知∠BED=∠B+∠D
试说明AB∥CD的理由.
