变量与函数第二课时
图片预览


文档简介
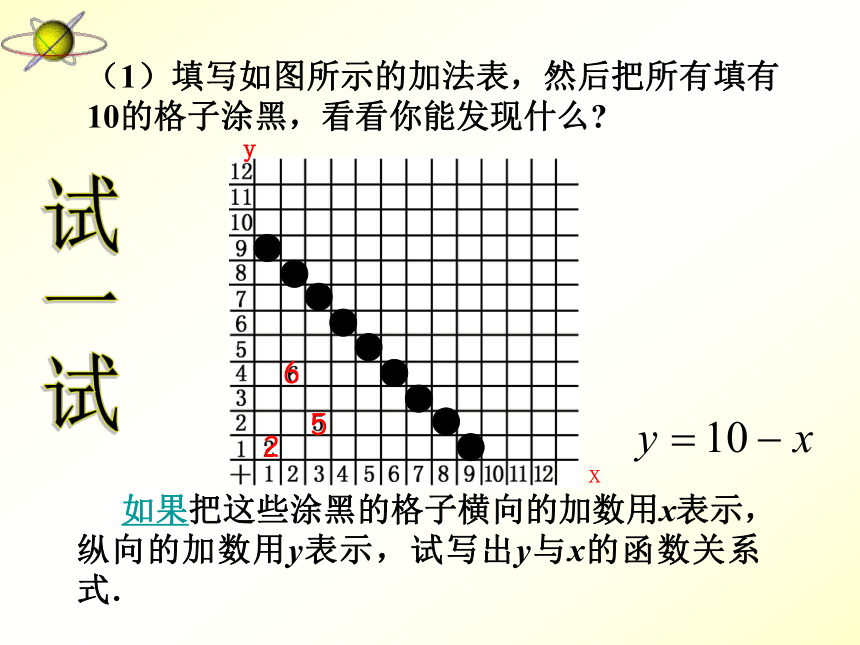
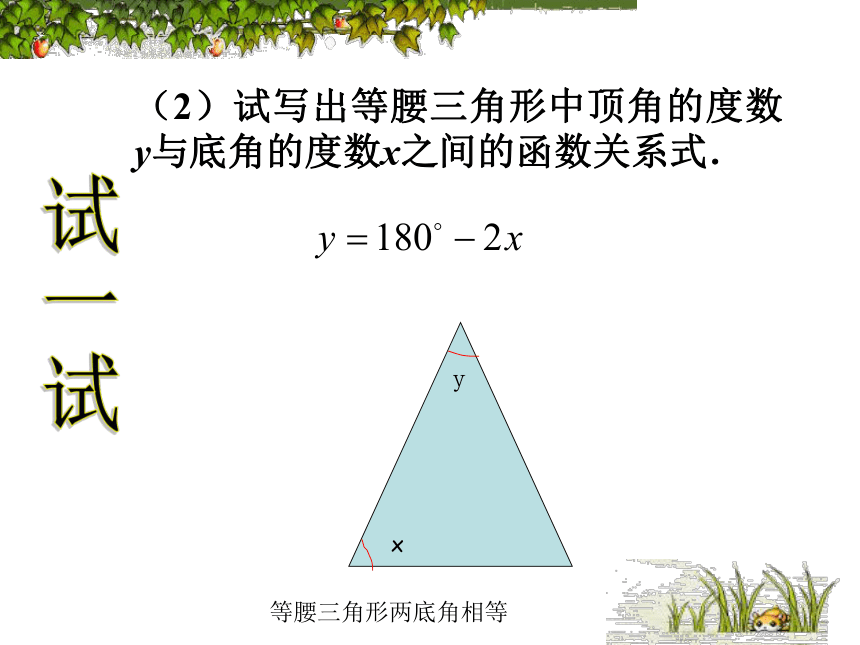
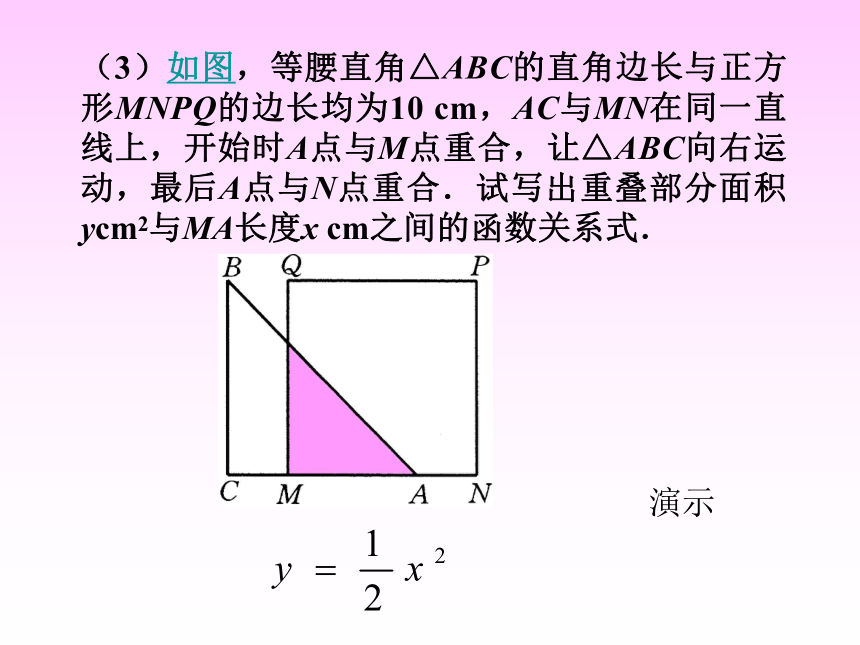
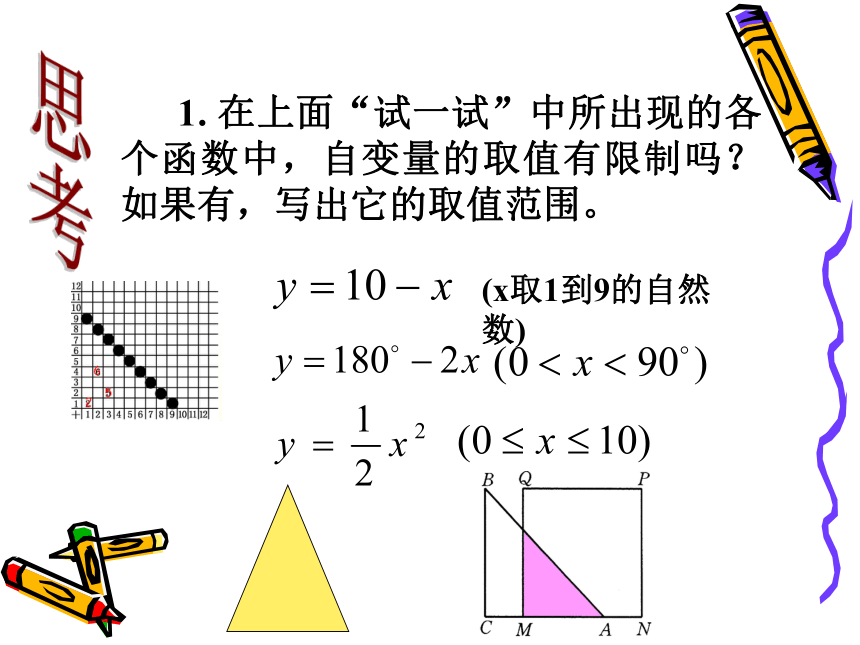
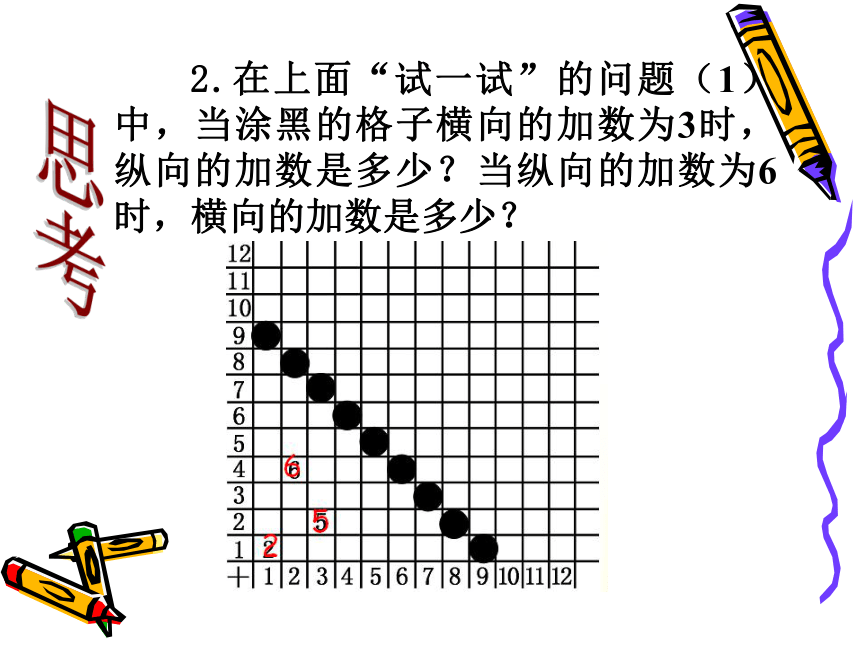
课件15张PPT。18.1变量与函数(2) 如果在一个变化过程中,有两个变量,如x和y,对于x的每一个值,y都有唯一的值与之对应,我们就说x是自变量,y是因变量,此时也称y是x的函数. ?函数关系的三种表示方法:解析法、列表法、图象法 在某一变化过程中,可以取不同数值的量,叫做变量.还有一种量,它的取值始终保持不变,称之为常量.复习(1)填写如图所示的加法表,然后把所有填有10的格子涂黑,看看你能发现什么? 如果把这些涂黑的格子横向的加数用x表示,纵向的加数用y表示,试写出y与x的函数关系式. 试一试256xy(2)试写出等腰三角形中顶角的度数y与底角的度数x之间的函数关系式. 试一试yx等腰三角形两底角相等(3)如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10 cm,AC与MN在同一直线上,开始时A点与M点重合,让△ABC向右运动,最后A点与N点重合.试写出重叠部分面积ycm2与MA长度x cm之间的函数关系式. 演示思考 1. 在上面“试一试”中所出现的各个函数中,自变量的取值有限制吗?如果有,写出它的取值范围。(x取1到9的自然数)思考 2.在上面“试一试”的问题(1)中,当涂黑的格子横向的加数为3时,纵向的加数是多少?当纵向的加数为6时,横向的加数是多少?例1 求下列函数中自变量x的取值范围:?(1) y=3x-1; (2) y=2x2+7; ?
(3) y= ; (4) y= . (1)(2)中x取任意实数,3x-1都有意义 (3)中,x≠-2时,原式有意义. ?(4)中x≥2时,原式有意义. 解:课内练习一:1.求下列函数中自变量x的取值范围 例2 在上面试一试的问题(3)中,当MA=1 cm时,重叠部分的面积是多少? ?解 :设重叠部分面积为y cm2,MA长为x cm y与x之间的函数关系式为 ?答:MA=1cm时,重叠部分的面积是 cm2课内练习二: 2.分别写出下列各问题中的函数关系式及自变量的取值范围:(1).某市民用电费标准为每度0.50元,求电费y(元)关于用电度数x的函数关系式; (2).已知等腰三角形的面积为20cm2,设它的底边长为x(cm),求底边上的高y(cm)关于x的函数关系式;(3).在一个半径为10 cm的圆形纸片中剪去一个半径为r(cm)的同心圆,得到一个圆环.设圆环的面积为S(cm2),求S关于r的函数关系式. 课内练习三:3.一架雪橇沿一斜坡滑下,它在时间t(秒)滑下的距离s(米)由下式给出:s=10t+2t2.假如滑到坡底的时间为8秒,试问坡长为多少? 1.已知长途汽车开始两小时的速度是45km/h,以后的速度是40km/h,写出汽车行驶的路程S(km)与时间t(h)的函数关系式,并写出自变量的取值范围.补充练习: 2.某小汽车的油箱可装油30L,每升汽油2.8元,该小汽车原有汽油10L,现再加汽油x L,求油箱内汽油的总价y(元)与x(L)之间的函数关系式,并写出自变量的取值范围.
(3) y= ; (4) y= . (1)(2)中x取任意实数,3x-1都有意义 (3)中,x≠-2时,原式有意义. ?(4)中x≥2时,原式有意义. 解:课内练习一:1.求下列函数中自变量x的取值范围 例2 在上面试一试的问题(3)中,当MA=1 cm时,重叠部分的面积是多少? ?解 :设重叠部分面积为y cm2,MA长为x cm y与x之间的函数关系式为 ?答:MA=1cm时,重叠部分的面积是 cm2课内练习二: 2.分别写出下列各问题中的函数关系式及自变量的取值范围:(1).某市民用电费标准为每度0.50元,求电费y(元)关于用电度数x的函数关系式; (2).已知等腰三角形的面积为20cm2,设它的底边长为x(cm),求底边上的高y(cm)关于x的函数关系式;(3).在一个半径为10 cm的圆形纸片中剪去一个半径为r(cm)的同心圆,得到一个圆环.设圆环的面积为S(cm2),求S关于r的函数关系式. 课内练习三:3.一架雪橇沿一斜坡滑下,它在时间t(秒)滑下的距离s(米)由下式给出:s=10t+2t2.假如滑到坡底的时间为8秒,试问坡长为多少? 1.已知长途汽车开始两小时的速度是45km/h,以后的速度是40km/h,写出汽车行驶的路程S(km)与时间t(h)的函数关系式,并写出自变量的取值范围.补充练习: 2.某小汽车的油箱可装油30L,每升汽油2.8元,该小汽车原有汽油10L,现再加汽油x L,求油箱内汽油的总价y(元)与x(L)之间的函数关系式,并写出自变量的取值范围.
