江苏省南京师范大学附属中学2023-2024学年高二上学期期末考试数学试卷(PDF版含答案)
文档属性
| 名称 | 江苏省南京师范大学附属中学2023-2024学年高二上学期期末考试数学试卷(PDF版含答案) |  | |
| 格式 | |||
| 文件大小 | 618.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 13:01:52 | ||
图片预览




文档简介
南京师大附中 2023-2024 学年度第一学期
高二年级期末考试数学试卷
班级________ 学号________ 姓名_________ 得分_________
注意事项:
1.本试卷共 4 页,包括单选题(第 1 题~第 8 题)、多选题(第 9 题~第 12 题)、填空题(第 13 题~
第 16 题)、解答题(第 17 题~第 22 题)四部分.本试卷满分为 150 分,考试时间为 120 分钟.
2.答题前,请务必将自己的姓名、班级、学号写在答题纸的密封线内.试题的答案写在答.题.
纸.上相应题目的答题区域内.考试结束后,交回答题纸.
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 直线 x + 3y +1= 0的倾斜角为
A. B. C. D.
6 3 3 6
a
2. 若数列{ n }是等差数列,且 a4 = 2, a8 =12 ,则 a = 12
n
9 5
A.30 B. C. 20 D.
2 2
3. 若函数 f (x) = sin x + 2xf '(0) ,则 f ' (0) =
A. 3 B. 1 C.1 D.3
3a
4. 若等比数列{a }的各项均为正数,且 2
a a + a
n ,
4 , a3 成等差数列,则
21 20 =
2 4 a18 + a17
A. 1 B.3 C.9 D. 27
5. 若定义在R 上的函数 y = x3 f '(x)的图象如图所示,则函数 y = f (x) 的增区间为
y = x3 f ' (x)
A.[0,1]
B.[0,2]
C. ( ,0]
D. ( , 2]
高二年级数学试卷 第 1 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
x2 y2 3
6. 已知点 M 在椭圆 + =1上,点 A(0, ), B(1,0),则MA+MB的最大值为
4 3 4
11 21
A. B. 4 C. D.5
4 4
x2 + 3x + 2, x≥ 1
7. 设 a R ,若函数 f (x) = ,关于 x 的方程 f (x) = a(x +1) 有且仅有 1 个实根,
ln ( x) , x 1
则 a 的取值范围为
A. ( , 1] [0,1] B.[ 1,0] [1,+ ) C.[ 1,1] D. ( , 1] [1,+ )
1+ 5 5a + b
8. 若数列{a },{b 满足 n n n ,且 ,则下列结论成立的是 n n} ( ) = an Z,bn Z
2 2
A. a2 = 3 B. n
*
N ,满足bn+2 = bn+1 + 2bn
C. n *N ,满足 (a 2 a a )2 =1 D. n
*
N ,使得 a b 成立
n+1 n n+2 n n
二、多项选择题:本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题
目要求. 全部选对的得 5 分,部分选对的得 2 分,有选错的得 0 分.
9. 设 k R ,若函数 f (x) = x3 kx2 k2x +5有且仅有一个零点,则 k 的值可以为
A. 3 B. 1 C.1 D. 2
10. 在等差数列{a }中,已知a1 = ,公差为 ,bn = cosan ,n cn = anbn ,则下列说法正确的是
n+1 1 ( 1)
n+1
A.bn = ( 1) B.b1 + b2 + b3 + + bn =
2
(2n +1) ( 1)n 1
C. c1 + c2 + c3 + + cn = D. c1 + c2 + c3 + + c2n = n
4
2 '
11. 若函数 f (x) = ,其导函数为 f (x),则下列说法正确的是
x
1+ e
'
A.函数 f (x)没有极值点 B. f (x)是奇函数
C.点 (0,1)是函数 f (x)的对称中心 D. x R , x[ f (x) 1]≥0
12. 过点M (4,0) 的直线与圆 (x + 2)2 + (y +5)2 = 25交于 A,B两点,在线段 AB上取一点 Q,使得
1 1 2
+ = ,则线段 MQ的长可以为
MA MB MQ
9 16 11 35
A. B. C. D.
2 3 2 6
高二年级数学试卷 第 2 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.
13. 设 S 为数列{an}的前 n项和,若 an = 3n 23,则 S 的最小值为_________ n n
14. 已知点 P 在直线 x y = 0 上,点 A(1,3) , B(3,4) ,则当△ABP的周长取得最小值时,点P 的坐
标为___________.
2 115. 设函数 f (x) = ln(x +1) ,则满足 f (x) f (2x +1)的 x的取值范围为__________.
x
16. 设 a R ,关于 x的不等式5e4x≥4(x + a)5 恒成立,则 a的最大值为__________.
四、解答题:本大题共 6 小题,共计 70 分.请在答题卡指定区域内作答,解答时应写出文字说明、
证明过程或演算步骤.
17.(10 分)
设 R ,Sn是数列{an}的前 n项和.已知a1 =1,an 0
*
,当 n N 时,满足 a a = S .
n n+1 n
(1)若 = ,求数列{an}的通项公式;
(2)是否存在 ,使得数列{an}为等差数列?若存在,求出 的值;若不存在,请说明理由.
18.(12 分)
3
x a +1 2
设 a为正实数,已知函数 f (x) = x + ax .
3 2
(1)若函数 f (x)有且仅有 2 个零点,求 a的值;
(2)当 x [0,3]时,函数 f (x) 的最小值为 0,求 a的取值范围.
19.(12 分)
x2 y2
设 k R ,在平面直角坐标系 xOy中,已知双曲线 =1的左焦点为 F,直线 y = k(x 2)与
2 2
双曲线的右支交于 A,B两点,与双曲线的渐近线交于 C,D两点.
(1)求 k的取值范围;
S
(2)记△AOB的面积为 S1,△CFD的面积为 S2,求 2 的取值范围.
S1
高二年级数学试卷 第 3 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
20.(12 分)
n, n为奇数
设 S 是数列{a }的前 n项和,已知数列{a }的通项公式为an =n n n n 2
2
2 , n为偶数.
(1)是否存在正整数 n,使得an = an+1 + an+2 成立?若存在,求出 n;若不存在,请说明理由;
(2)设 R ,若存在正整数 n,使得 S2n a 成立,求 的取值范围. 2n
21.(12 分)
设抛物线 x2 = 4y的焦点为 F,点 P 在抛物线的准线上. 过点 P 作抛物线的两条切线,切点分
别为 A,B. 已知抛物线上有一动点 C,位于点 A,B之间. 若抛物线在点 C处的切线与切线 PA,PB
相交于点M,N. 求证:
(1)直线 AB经过点 F;
(2)△PMN的外接圆过定点.
22.(12 分)
a
设 a ,已知函数 x 2R f (x) = e (x 1) x .
2
(1)讨论函数 f (x) 的单调性;
a
(2)设 k Z,若 f (x)…ln x x2 + k 恒成立,求 k的最大值.
2
高二年级数学试卷 第 4 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
南京师大附中 2023-2024 学年度第一学期
高二年级期末考试数学试卷答案
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.D 2.A 3.B 4.D 5.B 6.C
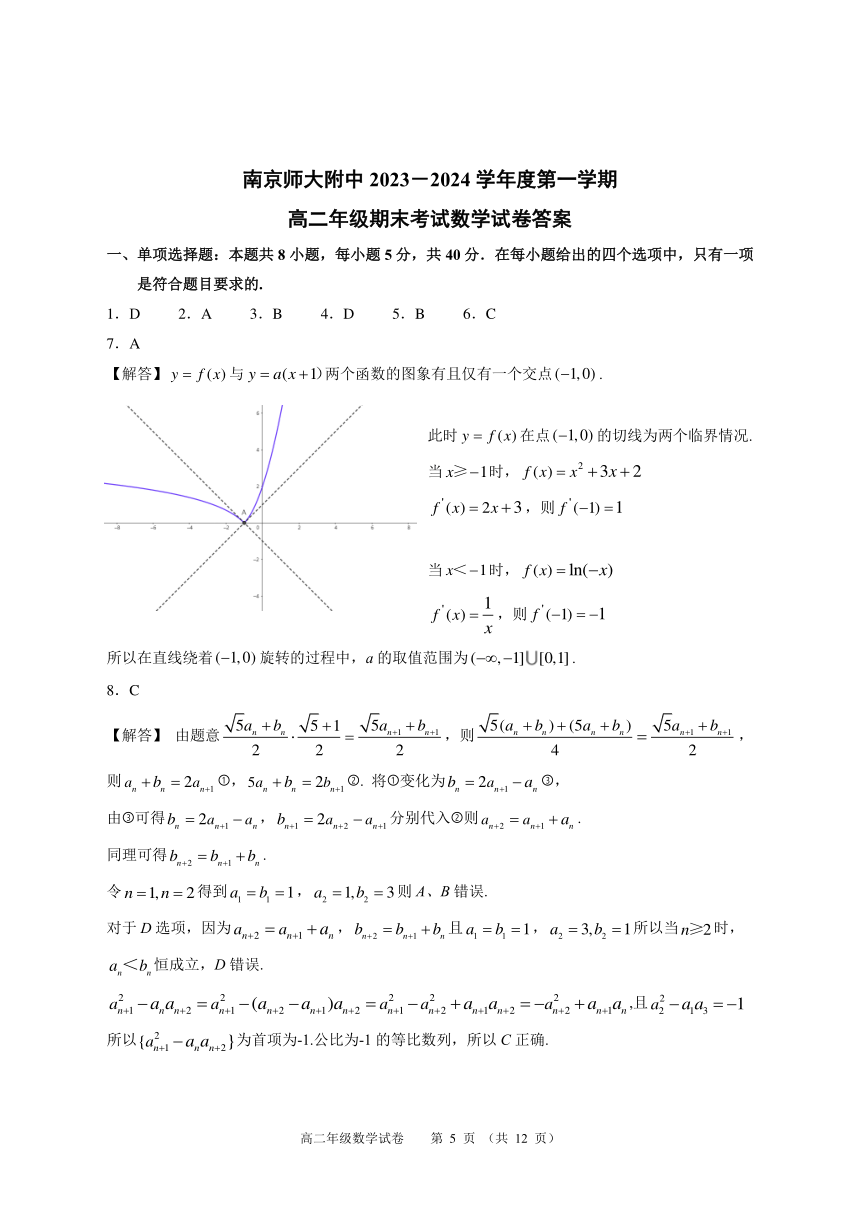
7.A
【解答】 y = f (x) 与 y = a(x +1)两个函数的图象有且仅有一个交点 ( 1, 0) .
此时 y = f (x) 在点 ( 1, 0) 的切线为两个临界情况.
2
当 x≥ 1时, f (x) = x +3x + 2
' '
f (x) = 2x +3,则 f ( 1) =1
当 x< 1时, f (x) = ln( x)
' 1 '
f (x) = ,则 f ( 1) = 1
x
所以在直线绕着 ( 1, 0) 旋转的过程中,a的取值范围为 ( , 1] [0,1] .
8.C
5a + b 5 +1 5a + b 5(a + b ) + (5a + b ) 5a + b
【解答】 由题意 n n = n+1 n+1 ,则 n n n n = n+1 n+1 ,
2 2 2 4 2
则 a + b = 2a ①,5a + b = 2b ②. 将①变化为b = 2a a ③,
n n n+1 n n n+1 n n+1 n
由③可得b = 2a a ,b = 2a a 分别代入②则 a = a + a .
n n+1 n n+1 n+2 n+1 n+2 n+1 n
同理可得b = b + b .
n+2 n+1 n
令 n =1,n = 2得到 a = b =1, a =1,b = 3则 A、B错误.
1 1 2 2
对于 D选项,因为 a ,n+2 = an+1 + an b = b + b 且 a = b =1, a = 3,b =1所以当n≥2时,n+2 n+1 n 1 1 2 2
a <b 恒成立,D错误.
n n
2 a a = 2a a (a a )a = 2 2 2a a +a a = a +a a ,且 2n+1 n n+2 n+1 n+2 n+1 n+2 n+1 n+2 n+1 n+2 n+2 n+1 n a2 a1a3 = 1
所以 2{an+1 a a }为首项为-1.公比为-1 的等比数列,所以 C正确. n n+2
高二年级数学试卷 第 5 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
二、多项选择题:本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题
目要求. 全部选对的得 4 分,部分选对的得 2 分,有选错的得 0 分.
9.BC 10.BCD
11.ACD
x
2 ' 2e
【解答】因为 f (x) = , f (x) = >0恒成立,所以 f (x) 在R 上单调递增,即 f (x) 不
x x 2
1+ e (1+ e )
存在极值点.
x x
' 2e 2e ' '
f (x) = = = f ( x),即 f (x)是偶函数.
x 2 x 2
(1+ e ) (1+ e )
x
2 2 2e 2
f (x) + f ( x) = + = + = 2 ,即 f (x) 关于点 (0,1)中心对称.
x x x x
1+ e 1+ e 1+ e 1+ e
因为 f (x)在R 上单调递增且 f (0) =1,所以当 x>0 时, f (x)>f (0) =1, x[ f (x) 1]>0 ,
当 x = 0时, x[ f (x) 1] = 0 ,当 x<0 时, f (x)<f (0) =1, x[ f (x) 1]>0 ,所以对于
x R, x[ f (x) 1]≥0 .
12. BCD
【解答】过点 M 作圆的一条切线,切点为 N. 取点 A,B 的中点为 R,设圆心到过点 M 的直线的
距离为 d (d [0,5)) .
由题意可得点 M 与圆心之间的距离为 61 .
2 2
根据圆的性质,MA MB = MN = 61 25 = 36 ,MA + MB = 2MR = 2 61 d .
1 1 2 2 MA+ MB 2MR 36 36
因为 + = ,所以 = = ,所以MQ = = .
MA MB MQ MQ MA MB 36 MR 261 d
36
当 d [0,5) 时,MQ [ , 6) .
61
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.
13. -77 14. (3,3)
1 1 1
15. ( 1, ) ( , )
2 2 3
2 1
【解答】 f (x) = ln(x +1) ,则 f (x) 时定义域为{x | x 0}的偶函数.
x
2 1 ' 2x 1
当 x>0 时, f (x) = ln(x +1) , f (x) = + >0恒成立.
2 2
x x +1 x
高二年级数学试卷 第 6 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
所以 f (x)在 ( , 0)上单调递减,在 (0,+ )上单调递增.
x 0
1 1 1
因为 f (x)>f (2x +1) ,所以 2x +1 0 ,故 x 的取值范围为 ( 1, ) ( , )
2 2 3
x > 2x +1
5 5
16. ln
4 4
4 x 5 5
【解答】方法一:令 g(x) = 5e , f (x) = 4(x + a) ,其中 f (x) 可以看作 y = 4x 左右平移得到.
因为 g(x)≥f (x)在R 上恒成立,所以当 g(x) , f (x) 具有公共切线时为临界情况.
' 4 x ' 4
因为 g (x) = 20e , f (x) = 20(x + a) ,不妨设公共切点为 (x , y )
0 0
' '
所以 g (x ) = f (x )且 g(x ) = f (x ) .
0 0 0 0
' ' 4x 4 x
当 g (x ) = f (x )时, 20e 0 = 20(x + a) ,即 e 0 = x + a;
0 0 0 0
4x 5 x 4 5
当 g(x ) = f (x ) 时,5e 0 = 4(x + a) ,将 e 0 = x + a代入,则5(x + a) = 4(x + a) ,即
0 0 0 0 0 0
5 x 5 5 5 5
x + a = = e 0 ,即 x = ln ,则 a = x = ln .
0 0 0
4 4 4 4 4
5 5
故 a 的最大值为 ln .
4 4
1
4x 5 5 4x
方法二:因为5e ≥4(x + a) 恒成立,所以 a≤( e )5 x .
4
1 4 4x 9 4x
5
( 4x)5 '
4 '' 4
令 f (x) = e x,则 f (x) = ( )5 e 5 1, f (x) = ( )5 e 5>0恒成立,
4 5 5
4 4x 4 4
' 4 ' 4 ' 5 4
则 f (x) = ( )5 e 5 1在R 上单调递增,且 f (0) = ( )5 1<0, f ( ) = ( )5 e 1>0,
5 5 4 5
4 4x0
则 ' '
5 ' 4 5
f (0) f ( )<0,所以存在唯一一个 x ,使得 f (x ) = ( )5 e 5 1= 0,且 x = ln .
0 0 0
4 5 4
5 5 5 5 5
所以 f (x)在 ( , ln )上单调递减,在 (ln ,+ ) 上单调递增,则 f = f (ln ) = ln ,
min
4 4 4 4 4
5 5
故 a≤ ln .
4 4
高二年级数学试卷 第 7 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
四、解答题:本大题共 6 小题,共计 70 分.请在答题卡指定区域内作答,解答时应写出文字说明、
证明过程或演算步骤.
17.(10 分)
(1)由 = 4,可得anan+1 = 4Sn ①,从而an+1an+2 = 4Sn+1②. ························· 2 分
②-①,可得an+1(an+2 an ) = 4an+1 . 因为an 0 ,所以an+2 an = 4 . ··············· 4 分
当n =1时,由a1 =1且anan+1 = 4Sn ,求得a2 =1.
2n 1, n为奇数;
所以,an = ··································································· 6 分
2n, n为偶数.
(2)由题设可知,a1 =1,a2 = , a3 =1+ .
若数列{an}为等差数列,则有2a2 = a1 + a3,解得 = 2. ································· 8 分
故有,anan+1 = 2Sn ,即an+2 an = 2.
又因为a1 =1,a2 = 2 ,所以an = n ,即数列{an}为等差数列. ······················· 10 分
18.(12 分)
3
x a +1 2 ' 2
(1) f (x) = x + ax , f (x) = x (a +1)x + a = (x 1)(x a)
3 2
' 2
①当 a = 1时, f (x) = (x 1) ≥0, f (x) 在R 上单调递增, f (x) 只有一个零点,则 a = 1不成立.
> '②当 a 1时,令 f (x) = 0 ,则 x =1或 x = a,且 a>1 .
'
当 x ( ,1) 时, f (x) 0 , f (x) 在 ( ,1) 上单调递增;
'
当 x (1, a) 时, f (x) 0, f (x)在 (1, a) 上单调递减;
'
当 x (a,+ )时, f (x) 0 , f (x)在 (a,+ ) 上单调递增.
函数 f (x)有且仅有两个零点,且 f (0) = 0 ,所以 f (a) = 0 ,即 a = 3 .
'
③当0<a<1时,令 f (x) = 0 ,则 x =1或 x = a,且 a<1 .
'
当 x ( , a)时, f (x) 0 , f (x)在 ( , a) 上单调递增;
'
当 x (a,1) 时, f (x) 0, f (x)在 (a,1) 上单调递减;
'
当 x (1,+ ) 时, f (x) 0 , f (x) 在 (1,+ ) 上单调递增.
1
函数 f (x)有且仅有两个零点,且 f (0) = 0 ,所以 f (1) = 0 ,即 a = .
3
1
综上所述:a的取值为 或3 .
3
高二年级数学试卷 第 8 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
(2)由(1)可知:
①当 a = 1时, f (x)在[0,3]上单调递增,则 f = f (0) = 0 ,故 a = 1成立.
min
②当 a>1时,
当 a≥3时, f (x)在[0,3]上单调递减,则 f = f (3)≥0,则 a≥3,故 a = 3;
min
当1<a<3时, f (x) 在[1, a) 上单调递减,在[a, 3]上单调递增,则 f = f (a)≥0,则1<a<3;
min
故1<a≤3.
1
③当0<a<1时, f (x)在[0,1]上单调递减,在[0,1]上单调递增,则 f = f (1)≥0 ,则 ≤a<1;
min
3
1
综上所述: ≤a≤3 .
3
19.(12 分)
x2 y2
=1
(1)由题设,联立方程组,可得 2 2 ,消去 y可得 (1 k
2 )x2 + 4k 2 x 4k 2 2 = 0 .
y = k(x 2)
0
2
4k
因为直线与双曲线的右支交于 A(x1,y1),B(x1,y1)两点,所以满足 x1 + x2 = 0 ,
k
2 1
4k 2 + 2
x1x2 = 0
k
2 1
··········································································································· 4 分
解得 k 1或 k 1 . ················································································· 5 分
S 2S
(2)由题设可知,△CFD面积为△COD面积的两倍,记△COD的面积为 S3,所以 2 = 3 .
S1 S1
················································································································· 7 分
S 2S 2CD
又因为△COD和△AOB的高相同,所以 2 = 3 = . ······························· 8 分
S1 S1 AB
x2 y2
= 0
由直线与双曲线的渐近线交于 C(x3,y3),D(x4,y4)两点,联立方程组,可得 2 2 ,消去 y
y = k(x 2)
4k 2 4k 2
可得 (1 k 2 )x2 + 4k 2x 4k 2 = 0 ,从而有 x3 + x4 = , x x = . ······················· 10 分
k 2
3 4
1 k 2 1
2
S 2CD 2 1+ k
2 | x 2 (x + x ) 4x x
2 3
x4 | 3 4 3 4 2 2从而有, = = = = .
S1 AB 1+ k
2 | x1 x2 | (x1 + x2 )
2 4x1x 12 1+
k 2
高二年级数学试卷 第 9 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
S
由(1)问可知, k 2 1,所以 2 (2, 2 2) . ··············································· 12 分
S1
20.(12 分)
(1)假设存在正整数 n,使得an = an+1 + an+2 .
当 n为偶数时,
n+2 2 n 2 n 2
因为 an+2=an+1+a ,所以 2 2n = 2 2 + n+1,即 2 2 = n +1.
若 n = 2 ,则左边=1,右边= 3,等式不成立;
若 n 2 ,则左边是偶数,右边是奇数,等式不成立.
当 n为奇数时,
n+1 2 n 1
因为 an+2=an+1+an,所以 n+ 2 = n+ 2 2 ,即 2 = 2 2 ,所以n = 3.
综上所述:存在正整数 n,使得an = an+1 + an+2 .正整数n = 3
(2)假设存在正整数 n,使得 S a . 2n 2n
2n 2
由题意可得 a 2 n 1; 2n = 2 = 2
S2n = a1 + a2 + + a2n = (a1 + a3 + + a 2n 1) + (a2 + a4 + + a2n )
= (1+3+ + 2n 1)+ (20 + 21 + + 2n 1) = n2 + 2n 1 .
2 n
当 时, n2 + 2n n 1
n + 2 1
S 1 2 ,即 . 2n a2n
2n 1
n2 + 2n 1 (n +1)2 + 2n+1 1 n2 + 2n 1 (n 1)2 + 3
令 bn = ,则bn 1 n+1 bn = = . 2 2n+1 1 2n 1 2n
当 n≥3时,bn+1 bn 0;当1≤n≤2时,bn+1 bn 0 .
则当 n = 3时,b 取得最大值,b . n 3 = 4
所以 4 .
21.(12 分)
1 1
(1)由题意,设 f (x) = x2 ,点 P(t, 1) , A(x1, y1) , B(x2 , y2 ) ,则 kPA = f '(x1) = x1 ,直线 PA
4 2
1
的方程为 y y1 = (x x1) ,且 x
2
1 = 4y1,化简得 x1x = 2y1 + 2y ①.
2
同理可得,切线 PB的方程为 x2 x = 2y2 + 2y ②. ··············································· 2 分
又因为切线 PA过点 P,所以有 x1t = 2y1 2;同理可得 x2t = 2y2 2 .
所以,直线 AB的方程为 tx = 2y 2,又点 F的坐标为(0,1),故直线 AB经过点 F.
··········································································································· 4 分
(2)设点C(x0 , y0 ) ,由(1)问可知在点 C处的切线方程为 x0 x = 2y0 + 2y .
高二年级数学试卷 第 10 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
x1x = 2y1 + 2y联立方程组,得 且 x 2
x + x x x
1 = 4y ,解得点M的坐标为 (
1 0 , 1 0 ) ,同理解得点 N的
1
x0 x = 2y0 + 2y 2 4
x + x x x
坐标为 ( 2 0 , 2 0 ) . ····················································································· 6 分
2 4
由(1)问可知,直线 AB 经过点 F,所以 PA⊥ PB,故线段 MN 即为△PMN 的外接圆的直径.
················································································································· 7 分
x2 = 4y
联立方程组 ,消去 y可得 x2 = 4(kx +1),从而有 x1 + x2 = 4k , x1x2 = 4 .
y = kx +1
··········································································································· 9 分
x + x x x x + x x x
因为 FM = ( 1 0 , 1 0 1), FN = ( 2 0 , 2 0 1),
2 4 2 4
x + x x x x + x x x x 2 2
FM FN = ( 1 0 , 1 0 1) ( 2 0 , 2 0 1) = 1
x2 + x0 (x1 + x2 ) + x0 x1x2x0 x+ 0
(x1 + x2 ) +1
2 4 2 4 4 16 4
将 x + x = 4k , x x = 4 代入上式,可得 FM FN = 01 2 1 2 ,所以△PMN的外接圆过定点 F.
······················································································································ 12 分
22.(12 分)
' x x
(1) f (x) = e x ax = x(e a)
'
①当 a≤0时,令 f (x) = 0 ,则 x = 0,所以
'
当 x ( , 0) 时, f (x) 0, f (x)在 ( , 0)上单调递增;
'
当 x (0,+ ) 时, f (x) 0 , f (x)在 (0,+ )上单调递减.
②当0 a 1时, ln a 0 ,所以
'
当 x ( , ln a) 时, f (x) 0 , f (x) 在 ( , ln a) 上单调递增;
'
当 x (ln a, 0) 时, f (x) 0, f (x)在 (ln a, 0) 上单调递减;
'
当 x (0,+ ) 时, f (x) 0 , f (x)在 (0,+ )上单调递增.
'
③当 a = 1时, ln a = 0, f (x) 0 ,则 f (x)在 ( ,+ ) 上单调递增.
④当 a 1时, ln a 0,所以
'
当 x ( , 0) 时, f (x) 0 , f (x)在 ( , 0)上单调递增;
'
当 x (0, ln a) 时, f (x) 0, f (x)在 (0, ln a)上单调递减;
'
当 x (ln a,+ )时, f (x) 0 , f (x)在 (ln a,+ ) 上单调递增.
综上所述:当 a≤0时, f (x)在 ( , 0)上单调递增, (0,+ )上单调递减;
当 0 a 1时, f (x)在 ( , ln a)上单调递增, (ln a, 0) 上单调递减, (0,+ )上单调递增;
当 a = 1时, f (x)在 ( ,+ ) 上单调递增;
高二年级数学试卷 第 11 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
当 a 1时, f (x)在 ( , 0)上单调递增, (0, ln a)上单调递减, (ln a,+ ) 上单调递增.
x 1
(2) ' xg(x) = e (x 1) ln x定义域为 (0,+ ) , g (x) = e x .
x
x 1 1 1设 h(x) = e x ,则
x
h(x) = e (x +1) + 0 恒成立,则
x
h(x) = e x 在 (0,+ )上单调递增.
2
x x x
3 3
3 3 5 3 3 4
又 h( ) = e5 0, h( ) = e4 0 .
5 5 3 4 4 3
3 3 3
3 5 25 25
【理由: e5 e5 ,而 e5 e < 2.72 < ;
5 3 9 9
3 3
3 4 16 3 164 4 3 16 4e e4 e ( ) 而 e 16 ( ) 】
4 3 9 9 9
3 3 x 1
所以存在唯一 x ( , ) ,使得 h(x ) = e 0 x = 0,且 g(x) 在 (0, x ) 上单调递减,在 (x ,+ )上
0 0 0 0 0
5 4 x
0
单调递增.
x 1 x 1 1 x 1 x
因为 h(x ) = e 0 x = 0,所以 e 0 = , x = ln = 2 ln x ,即 e 0 = 且 ln x = 0 .
0 0 2 0 2 0 2 0
x x x x
0 0 0
2
0
x x 1 x
所以 g(x) = g(x ) = e 0 (x 1) ln x = 0 + 0 .
min 0 0 0 2
x 2
0
3 3
x 1 x x + 2x 2 ' x 2x + 2
令 M (x) = + = ,则M (x) = .
2 2 3
x 2 2x 2x
3
3 3 ' x 2x + 2
当 x ( , ),M (x) = 0恒成立,
3
5 4 2x
3 3 3 73 3 5 73 5
所以M (x) 在 ( , )上单调递增,且M ( ) = ,M ( ) = ,所以M (x ) ( , )
0
5 4 5 90 4 72 90 72
所以整数 k的最大值为 1.
高二年级数学试卷 第 12 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
高二年级期末考试数学试卷
班级________ 学号________ 姓名_________ 得分_________
注意事项:
1.本试卷共 4 页,包括单选题(第 1 题~第 8 题)、多选题(第 9 题~第 12 题)、填空题(第 13 题~
第 16 题)、解答题(第 17 题~第 22 题)四部分.本试卷满分为 150 分,考试时间为 120 分钟.
2.答题前,请务必将自己的姓名、班级、学号写在答题纸的密封线内.试题的答案写在答.题.
纸.上相应题目的答题区域内.考试结束后,交回答题纸.
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 直线 x + 3y +1= 0的倾斜角为
A. B. C. D.
6 3 3 6
a
2. 若数列{ n }是等差数列,且 a4 = 2, a8 =12 ,则 a = 12
n
9 5
A.30 B. C. 20 D.
2 2
3. 若函数 f (x) = sin x + 2xf '(0) ,则 f ' (0) =
A. 3 B. 1 C.1 D.3
3a
4. 若等比数列{a }的各项均为正数,且 2
a a + a
n ,
4 , a3 成等差数列,则
21 20 =
2 4 a18 + a17
A. 1 B.3 C.9 D. 27
5. 若定义在R 上的函数 y = x3 f '(x)的图象如图所示,则函数 y = f (x) 的增区间为
y = x3 f ' (x)
A.[0,1]
B.[0,2]
C. ( ,0]
D. ( , 2]
高二年级数学试卷 第 1 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
x2 y2 3
6. 已知点 M 在椭圆 + =1上,点 A(0, ), B(1,0),则MA+MB的最大值为
4 3 4
11 21
A. B. 4 C. D.5
4 4
x2 + 3x + 2, x≥ 1
7. 设 a R ,若函数 f (x) = ,关于 x 的方程 f (x) = a(x +1) 有且仅有 1 个实根,
ln ( x) , x 1
则 a 的取值范围为
A. ( , 1] [0,1] B.[ 1,0] [1,+ ) C.[ 1,1] D. ( , 1] [1,+ )
1+ 5 5a + b
8. 若数列{a },{b 满足 n n n ,且 ,则下列结论成立的是 n n} ( ) = an Z,bn Z
2 2
A. a2 = 3 B. n
*
N ,满足bn+2 = bn+1 + 2bn
C. n *N ,满足 (a 2 a a )2 =1 D. n
*
N ,使得 a b 成立
n+1 n n+2 n n
二、多项选择题:本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题
目要求. 全部选对的得 5 分,部分选对的得 2 分,有选错的得 0 分.
9. 设 k R ,若函数 f (x) = x3 kx2 k2x +5有且仅有一个零点,则 k 的值可以为
A. 3 B. 1 C.1 D. 2
10. 在等差数列{a }中,已知a1 = ,公差为 ,bn = cosan ,n cn = anbn ,则下列说法正确的是
n+1 1 ( 1)
n+1
A.bn = ( 1) B.b1 + b2 + b3 + + bn =
2
(2n +1) ( 1)n 1
C. c1 + c2 + c3 + + cn = D. c1 + c2 + c3 + + c2n = n
4
2 '
11. 若函数 f (x) = ,其导函数为 f (x),则下列说法正确的是
x
1+ e
'
A.函数 f (x)没有极值点 B. f (x)是奇函数
C.点 (0,1)是函数 f (x)的对称中心 D. x R , x[ f (x) 1]≥0
12. 过点M (4,0) 的直线与圆 (x + 2)2 + (y +5)2 = 25交于 A,B两点,在线段 AB上取一点 Q,使得
1 1 2
+ = ,则线段 MQ的长可以为
MA MB MQ
9 16 11 35
A. B. C. D.
2 3 2 6
高二年级数学试卷 第 2 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.
13. 设 S 为数列{an}的前 n项和,若 an = 3n 23,则 S 的最小值为_________ n n
14. 已知点 P 在直线 x y = 0 上,点 A(1,3) , B(3,4) ,则当△ABP的周长取得最小值时,点P 的坐
标为___________.
2 115. 设函数 f (x) = ln(x +1) ,则满足 f (x) f (2x +1)的 x的取值范围为__________.
x
16. 设 a R ,关于 x的不等式5e4x≥4(x + a)5 恒成立,则 a的最大值为__________.
四、解答题:本大题共 6 小题,共计 70 分.请在答题卡指定区域内作答,解答时应写出文字说明、
证明过程或演算步骤.
17.(10 分)
设 R ,Sn是数列{an}的前 n项和.已知a1 =1,an 0
*
,当 n N 时,满足 a a = S .
n n+1 n
(1)若 = ,求数列{an}的通项公式;
(2)是否存在 ,使得数列{an}为等差数列?若存在,求出 的值;若不存在,请说明理由.
18.(12 分)
3
x a +1 2
设 a为正实数,已知函数 f (x) = x + ax .
3 2
(1)若函数 f (x)有且仅有 2 个零点,求 a的值;
(2)当 x [0,3]时,函数 f (x) 的最小值为 0,求 a的取值范围.
19.(12 分)
x2 y2
设 k R ,在平面直角坐标系 xOy中,已知双曲线 =1的左焦点为 F,直线 y = k(x 2)与
2 2
双曲线的右支交于 A,B两点,与双曲线的渐近线交于 C,D两点.
(1)求 k的取值范围;
S
(2)记△AOB的面积为 S1,△CFD的面积为 S2,求 2 的取值范围.
S1
高二年级数学试卷 第 3 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
20.(12 分)
n, n为奇数
设 S 是数列{a }的前 n项和,已知数列{a }的通项公式为an =n n n n 2
2
2 , n为偶数.
(1)是否存在正整数 n,使得an = an+1 + an+2 成立?若存在,求出 n;若不存在,请说明理由;
(2)设 R ,若存在正整数 n,使得 S2n a 成立,求 的取值范围. 2n
21.(12 分)
设抛物线 x2 = 4y的焦点为 F,点 P 在抛物线的准线上. 过点 P 作抛物线的两条切线,切点分
别为 A,B. 已知抛物线上有一动点 C,位于点 A,B之间. 若抛物线在点 C处的切线与切线 PA,PB
相交于点M,N. 求证:
(1)直线 AB经过点 F;
(2)△PMN的外接圆过定点.
22.(12 分)
a
设 a ,已知函数 x 2R f (x) = e (x 1) x .
2
(1)讨论函数 f (x) 的单调性;
a
(2)设 k Z,若 f (x)…ln x x2 + k 恒成立,求 k的最大值.
2
高二年级数学试卷 第 4 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
南京师大附中 2023-2024 学年度第一学期
高二年级期末考试数学试卷答案
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1.D 2.A 3.B 4.D 5.B 6.C
7.A
【解答】 y = f (x) 与 y = a(x +1)两个函数的图象有且仅有一个交点 ( 1, 0) .
此时 y = f (x) 在点 ( 1, 0) 的切线为两个临界情况.
2
当 x≥ 1时, f (x) = x +3x + 2
' '
f (x) = 2x +3,则 f ( 1) =1
当 x< 1时, f (x) = ln( x)
' 1 '
f (x) = ,则 f ( 1) = 1
x
所以在直线绕着 ( 1, 0) 旋转的过程中,a的取值范围为 ( , 1] [0,1] .
8.C
5a + b 5 +1 5a + b 5(a + b ) + (5a + b ) 5a + b
【解答】 由题意 n n = n+1 n+1 ,则 n n n n = n+1 n+1 ,
2 2 2 4 2
则 a + b = 2a ①,5a + b = 2b ②. 将①变化为b = 2a a ③,
n n n+1 n n n+1 n n+1 n
由③可得b = 2a a ,b = 2a a 分别代入②则 a = a + a .
n n+1 n n+1 n+2 n+1 n+2 n+1 n
同理可得b = b + b .
n+2 n+1 n
令 n =1,n = 2得到 a = b =1, a =1,b = 3则 A、B错误.
1 1 2 2
对于 D选项,因为 a ,n+2 = an+1 + an b = b + b 且 a = b =1, a = 3,b =1所以当n≥2时,n+2 n+1 n 1 1 2 2
a <b 恒成立,D错误.
n n
2 a a = 2a a (a a )a = 2 2 2a a +a a = a +a a ,且 2n+1 n n+2 n+1 n+2 n+1 n+2 n+1 n+2 n+1 n+2 n+2 n+1 n a2 a1a3 = 1
所以 2{an+1 a a }为首项为-1.公比为-1 的等比数列,所以 C正确. n n+2
高二年级数学试卷 第 5 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
二、多项选择题:本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题
目要求. 全部选对的得 4 分,部分选对的得 2 分,有选错的得 0 分.
9.BC 10.BCD
11.ACD
x
2 ' 2e
【解答】因为 f (x) = , f (x) = >0恒成立,所以 f (x) 在R 上单调递增,即 f (x) 不
x x 2
1+ e (1+ e )
存在极值点.
x x
' 2e 2e ' '
f (x) = = = f ( x),即 f (x)是偶函数.
x 2 x 2
(1+ e ) (1+ e )
x
2 2 2e 2
f (x) + f ( x) = + = + = 2 ,即 f (x) 关于点 (0,1)中心对称.
x x x x
1+ e 1+ e 1+ e 1+ e
因为 f (x)在R 上单调递增且 f (0) =1,所以当 x>0 时, f (x)>f (0) =1, x[ f (x) 1]>0 ,
当 x = 0时, x[ f (x) 1] = 0 ,当 x<0 时, f (x)<f (0) =1, x[ f (x) 1]>0 ,所以对于
x R, x[ f (x) 1]≥0 .
12. BCD
【解答】过点 M 作圆的一条切线,切点为 N. 取点 A,B 的中点为 R,设圆心到过点 M 的直线的
距离为 d (d [0,5)) .
由题意可得点 M 与圆心之间的距离为 61 .
2 2
根据圆的性质,MA MB = MN = 61 25 = 36 ,MA + MB = 2MR = 2 61 d .
1 1 2 2 MA+ MB 2MR 36 36
因为 + = ,所以 = = ,所以MQ = = .
MA MB MQ MQ MA MB 36 MR 261 d
36
当 d [0,5) 时,MQ [ , 6) .
61
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.
13. -77 14. (3,3)
1 1 1
15. ( 1, ) ( , )
2 2 3
2 1
【解答】 f (x) = ln(x +1) ,则 f (x) 时定义域为{x | x 0}的偶函数.
x
2 1 ' 2x 1
当 x>0 时, f (x) = ln(x +1) , f (x) = + >0恒成立.
2 2
x x +1 x
高二年级数学试卷 第 6 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
所以 f (x)在 ( , 0)上单调递减,在 (0,+ )上单调递增.
x 0
1 1 1
因为 f (x)>f (2x +1) ,所以 2x +1 0 ,故 x 的取值范围为 ( 1, ) ( , )
2 2 3
x > 2x +1
5 5
16. ln
4 4
4 x 5 5
【解答】方法一:令 g(x) = 5e , f (x) = 4(x + a) ,其中 f (x) 可以看作 y = 4x 左右平移得到.
因为 g(x)≥f (x)在R 上恒成立,所以当 g(x) , f (x) 具有公共切线时为临界情况.
' 4 x ' 4
因为 g (x) = 20e , f (x) = 20(x + a) ,不妨设公共切点为 (x , y )
0 0
' '
所以 g (x ) = f (x )且 g(x ) = f (x ) .
0 0 0 0
' ' 4x 4 x
当 g (x ) = f (x )时, 20e 0 = 20(x + a) ,即 e 0 = x + a;
0 0 0 0
4x 5 x 4 5
当 g(x ) = f (x ) 时,5e 0 = 4(x + a) ,将 e 0 = x + a代入,则5(x + a) = 4(x + a) ,即
0 0 0 0 0 0
5 x 5 5 5 5
x + a = = e 0 ,即 x = ln ,则 a = x = ln .
0 0 0
4 4 4 4 4
5 5
故 a 的最大值为 ln .
4 4
1
4x 5 5 4x
方法二:因为5e ≥4(x + a) 恒成立,所以 a≤( e )5 x .
4
1 4 4x 9 4x
5
( 4x)5 '
4 '' 4
令 f (x) = e x,则 f (x) = ( )5 e 5 1, f (x) = ( )5 e 5>0恒成立,
4 5 5
4 4x 4 4
' 4 ' 4 ' 5 4
则 f (x) = ( )5 e 5 1在R 上单调递增,且 f (0) = ( )5 1<0, f ( ) = ( )5 e 1>0,
5 5 4 5
4 4x0
则 ' '
5 ' 4 5
f (0) f ( )<0,所以存在唯一一个 x ,使得 f (x ) = ( )5 e 5 1= 0,且 x = ln .
0 0 0
4 5 4
5 5 5 5 5
所以 f (x)在 ( , ln )上单调递减,在 (ln ,+ ) 上单调递增,则 f = f (ln ) = ln ,
min
4 4 4 4 4
5 5
故 a≤ ln .
4 4
高二年级数学试卷 第 7 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
四、解答题:本大题共 6 小题,共计 70 分.请在答题卡指定区域内作答,解答时应写出文字说明、
证明过程或演算步骤.
17.(10 分)
(1)由 = 4,可得anan+1 = 4Sn ①,从而an+1an+2 = 4Sn+1②. ························· 2 分
②-①,可得an+1(an+2 an ) = 4an+1 . 因为an 0 ,所以an+2 an = 4 . ··············· 4 分
当n =1时,由a1 =1且anan+1 = 4Sn ,求得a2 =1.
2n 1, n为奇数;
所以,an = ··································································· 6 分
2n, n为偶数.
(2)由题设可知,a1 =1,a2 = , a3 =1+ .
若数列{an}为等差数列,则有2a2 = a1 + a3,解得 = 2. ································· 8 分
故有,anan+1 = 2Sn ,即an+2 an = 2.
又因为a1 =1,a2 = 2 ,所以an = n ,即数列{an}为等差数列. ······················· 10 分
18.(12 分)
3
x a +1 2 ' 2
(1) f (x) = x + ax , f (x) = x (a +1)x + a = (x 1)(x a)
3 2
' 2
①当 a = 1时, f (x) = (x 1) ≥0, f (x) 在R 上单调递增, f (x) 只有一个零点,则 a = 1不成立.
> '②当 a 1时,令 f (x) = 0 ,则 x =1或 x = a,且 a>1 .
'
当 x ( ,1) 时, f (x) 0 , f (x) 在 ( ,1) 上单调递增;
'
当 x (1, a) 时, f (x) 0, f (x)在 (1, a) 上单调递减;
'
当 x (a,+ )时, f (x) 0 , f (x)在 (a,+ ) 上单调递增.
函数 f (x)有且仅有两个零点,且 f (0) = 0 ,所以 f (a) = 0 ,即 a = 3 .
'
③当0<a<1时,令 f (x) = 0 ,则 x =1或 x = a,且 a<1 .
'
当 x ( , a)时, f (x) 0 , f (x)在 ( , a) 上单调递增;
'
当 x (a,1) 时, f (x) 0, f (x)在 (a,1) 上单调递减;
'
当 x (1,+ ) 时, f (x) 0 , f (x) 在 (1,+ ) 上单调递增.
1
函数 f (x)有且仅有两个零点,且 f (0) = 0 ,所以 f (1) = 0 ,即 a = .
3
1
综上所述:a的取值为 或3 .
3
高二年级数学试卷 第 8 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
(2)由(1)可知:
①当 a = 1时, f (x)在[0,3]上单调递增,则 f = f (0) = 0 ,故 a = 1成立.
min
②当 a>1时,
当 a≥3时, f (x)在[0,3]上单调递减,则 f = f (3)≥0,则 a≥3,故 a = 3;
min
当1<a<3时, f (x) 在[1, a) 上单调递减,在[a, 3]上单调递增,则 f = f (a)≥0,则1<a<3;
min
故1<a≤3.
1
③当0<a<1时, f (x)在[0,1]上单调递减,在[0,1]上单调递增,则 f = f (1)≥0 ,则 ≤a<1;
min
3
1
综上所述: ≤a≤3 .
3
19.(12 分)
x2 y2
=1
(1)由题设,联立方程组,可得 2 2 ,消去 y可得 (1 k
2 )x2 + 4k 2 x 4k 2 2 = 0 .
y = k(x 2)
0
2
4k
因为直线与双曲线的右支交于 A(x1,y1),B(x1,y1)两点,所以满足 x1 + x2 = 0 ,
k
2 1
4k 2 + 2
x1x2 = 0
k
2 1
··········································································································· 4 分
解得 k 1或 k 1 . ················································································· 5 分
S 2S
(2)由题设可知,△CFD面积为△COD面积的两倍,记△COD的面积为 S3,所以 2 = 3 .
S1 S1
················································································································· 7 分
S 2S 2CD
又因为△COD和△AOB的高相同,所以 2 = 3 = . ······························· 8 分
S1 S1 AB
x2 y2
= 0
由直线与双曲线的渐近线交于 C(x3,y3),D(x4,y4)两点,联立方程组,可得 2 2 ,消去 y
y = k(x 2)
4k 2 4k 2
可得 (1 k 2 )x2 + 4k 2x 4k 2 = 0 ,从而有 x3 + x4 = , x x = . ······················· 10 分
k 2
3 4
1 k 2 1
2
S 2CD 2 1+ k
2 | x 2 (x + x ) 4x x
2 3
x4 | 3 4 3 4 2 2从而有, = = = = .
S1 AB 1+ k
2 | x1 x2 | (x1 + x2 )
2 4x1x 12 1+
k 2
高二年级数学试卷 第 9 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
S
由(1)问可知, k 2 1,所以 2 (2, 2 2) . ··············································· 12 分
S1
20.(12 分)
(1)假设存在正整数 n,使得an = an+1 + an+2 .
当 n为偶数时,
n+2 2 n 2 n 2
因为 an+2=an+1+a ,所以 2 2n = 2 2 + n+1,即 2 2 = n +1.
若 n = 2 ,则左边=1,右边= 3,等式不成立;
若 n 2 ,则左边是偶数,右边是奇数,等式不成立.
当 n为奇数时,
n+1 2 n 1
因为 an+2=an+1+an,所以 n+ 2 = n+ 2 2 ,即 2 = 2 2 ,所以n = 3.
综上所述:存在正整数 n,使得an = an+1 + an+2 .正整数n = 3
(2)假设存在正整数 n,使得 S a . 2n 2n
2n 2
由题意可得 a 2 n 1; 2n = 2 = 2
S2n = a1 + a2 + + a2n = (a1 + a3 + + a 2n 1) + (a2 + a4 + + a2n )
= (1+3+ + 2n 1)+ (20 + 21 + + 2n 1) = n2 + 2n 1 .
2 n
当 时, n2 + 2n n 1
n + 2 1
S 1 2 ,即 . 2n a2n
2n 1
n2 + 2n 1 (n +1)2 + 2n+1 1 n2 + 2n 1 (n 1)2 + 3
令 bn = ,则bn 1 n+1 bn = = . 2 2n+1 1 2n 1 2n
当 n≥3时,bn+1 bn 0;当1≤n≤2时,bn+1 bn 0 .
则当 n = 3时,b 取得最大值,b . n 3 = 4
所以 4 .
21.(12 分)
1 1
(1)由题意,设 f (x) = x2 ,点 P(t, 1) , A(x1, y1) , B(x2 , y2 ) ,则 kPA = f '(x1) = x1 ,直线 PA
4 2
1
的方程为 y y1 = (x x1) ,且 x
2
1 = 4y1,化简得 x1x = 2y1 + 2y ①.
2
同理可得,切线 PB的方程为 x2 x = 2y2 + 2y ②. ··············································· 2 分
又因为切线 PA过点 P,所以有 x1t = 2y1 2;同理可得 x2t = 2y2 2 .
所以,直线 AB的方程为 tx = 2y 2,又点 F的坐标为(0,1),故直线 AB经过点 F.
··········································································································· 4 分
(2)设点C(x0 , y0 ) ,由(1)问可知在点 C处的切线方程为 x0 x = 2y0 + 2y .
高二年级数学试卷 第 10 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
x1x = 2y1 + 2y联立方程组,得 且 x 2
x + x x x
1 = 4y ,解得点M的坐标为 (
1 0 , 1 0 ) ,同理解得点 N的
1
x0 x = 2y0 + 2y 2 4
x + x x x
坐标为 ( 2 0 , 2 0 ) . ····················································································· 6 分
2 4
由(1)问可知,直线 AB 经过点 F,所以 PA⊥ PB,故线段 MN 即为△PMN 的外接圆的直径.
················································································································· 7 分
x2 = 4y
联立方程组 ,消去 y可得 x2 = 4(kx +1),从而有 x1 + x2 = 4k , x1x2 = 4 .
y = kx +1
··········································································································· 9 分
x + x x x x + x x x
因为 FM = ( 1 0 , 1 0 1), FN = ( 2 0 , 2 0 1),
2 4 2 4
x + x x x x + x x x x 2 2
FM FN = ( 1 0 , 1 0 1) ( 2 0 , 2 0 1) = 1
x2 + x0 (x1 + x2 ) + x0 x1x2x0 x+ 0
(x1 + x2 ) +1
2 4 2 4 4 16 4
将 x + x = 4k , x x = 4 代入上式,可得 FM FN = 01 2 1 2 ,所以△PMN的外接圆过定点 F.
······················································································································ 12 分
22.(12 分)
' x x
(1) f (x) = e x ax = x(e a)
'
①当 a≤0时,令 f (x) = 0 ,则 x = 0,所以
'
当 x ( , 0) 时, f (x) 0, f (x)在 ( , 0)上单调递增;
'
当 x (0,+ ) 时, f (x) 0 , f (x)在 (0,+ )上单调递减.
②当0 a 1时, ln a 0 ,所以
'
当 x ( , ln a) 时, f (x) 0 , f (x) 在 ( , ln a) 上单调递增;
'
当 x (ln a, 0) 时, f (x) 0, f (x)在 (ln a, 0) 上单调递减;
'
当 x (0,+ ) 时, f (x) 0 , f (x)在 (0,+ )上单调递增.
'
③当 a = 1时, ln a = 0, f (x) 0 ,则 f (x)在 ( ,+ ) 上单调递增.
④当 a 1时, ln a 0,所以
'
当 x ( , 0) 时, f (x) 0 , f (x)在 ( , 0)上单调递增;
'
当 x (0, ln a) 时, f (x) 0, f (x)在 (0, ln a)上单调递减;
'
当 x (ln a,+ )时, f (x) 0 , f (x)在 (ln a,+ ) 上单调递增.
综上所述:当 a≤0时, f (x)在 ( , 0)上单调递增, (0,+ )上单调递减;
当 0 a 1时, f (x)在 ( , ln a)上单调递增, (ln a, 0) 上单调递减, (0,+ )上单调递增;
当 a = 1时, f (x)在 ( ,+ ) 上单调递增;
高二年级数学试卷 第 11 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
当 a 1时, f (x)在 ( , 0)上单调递增, (0, ln a)上单调递减, (ln a,+ ) 上单调递增.
x 1
(2) ' xg(x) = e (x 1) ln x定义域为 (0,+ ) , g (x) = e x .
x
x 1 1 1设 h(x) = e x ,则
x
h(x) = e (x +1) + 0 恒成立,则
x
h(x) = e x 在 (0,+ )上单调递增.
2
x x x
3 3
3 3 5 3 3 4
又 h( ) = e5 0, h( ) = e4 0 .
5 5 3 4 4 3
3 3 3
3 5 25 25
【理由: e5 e5 ,而 e5 e < 2.72 < ;
5 3 9 9
3 3
3 4 16 3 164 4 3 16 4e e4 e ( ) 而 e 16 ( ) 】
4 3 9 9 9
3 3 x 1
所以存在唯一 x ( , ) ,使得 h(x ) = e 0 x = 0,且 g(x) 在 (0, x ) 上单调递减,在 (x ,+ )上
0 0 0 0 0
5 4 x
0
单调递增.
x 1 x 1 1 x 1 x
因为 h(x ) = e 0 x = 0,所以 e 0 = , x = ln = 2 ln x ,即 e 0 = 且 ln x = 0 .
0 0 2 0 2 0 2 0
x x x x
0 0 0
2
0
x x 1 x
所以 g(x) = g(x ) = e 0 (x 1) ln x = 0 + 0 .
min 0 0 0 2
x 2
0
3 3
x 1 x x + 2x 2 ' x 2x + 2
令 M (x) = + = ,则M (x) = .
2 2 3
x 2 2x 2x
3
3 3 ' x 2x + 2
当 x ( , ),M (x) = 0恒成立,
3
5 4 2x
3 3 3 73 3 5 73 5
所以M (x) 在 ( , )上单调递增,且M ( ) = ,M ( ) = ,所以M (x ) ( , )
0
5 4 5 90 4 72 90 72
所以整数 k的最大值为 1.
高二年级数学试卷 第 12 页 (共 12 页)
{#{QQABAQSEggggAAJAAQhCQwlaCECQkACAAAoGQEAEoAAAyRNABAA=}#}
同课章节目录
