六年级下册数学苏教版第1课时线与角(课件)(共48张PPT)
文档属性
| 名称 | 六年级下册数学苏教版第1课时线与角(课件)(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 10:26:30 | ||
图片预览









文档简介
(共48张PPT)
线与角
“五线”——直线、射线、线段、垂线、平行线;
“五角”——锐角、直角、钝角、平角、周角。
A
A
B
A
B
A
B
线段
名称 图 形 联 系 区 别
射线
直线
⑴都是直的
⑵线段是射
线或直线的
一部分
有两个端点
有一个端点
没有端点
①线段、射线和直线的长度有限吗?为什么?
②过一点能画几条直线?几条射线?
③过两点能几条直线?直线上两点之间的部分是什么?
一、线段、射线和直线。
要把一根细木条固定在墙上,至少要几枚钉子?为什么?
小知识,大学问。
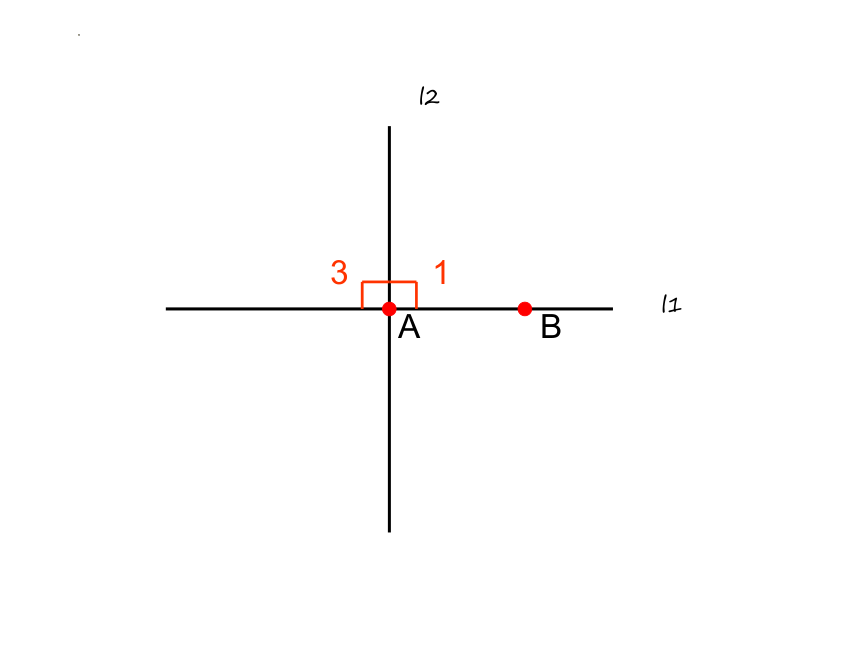
l1
l2
A
B
1
3
l1
l2
A
B
平角
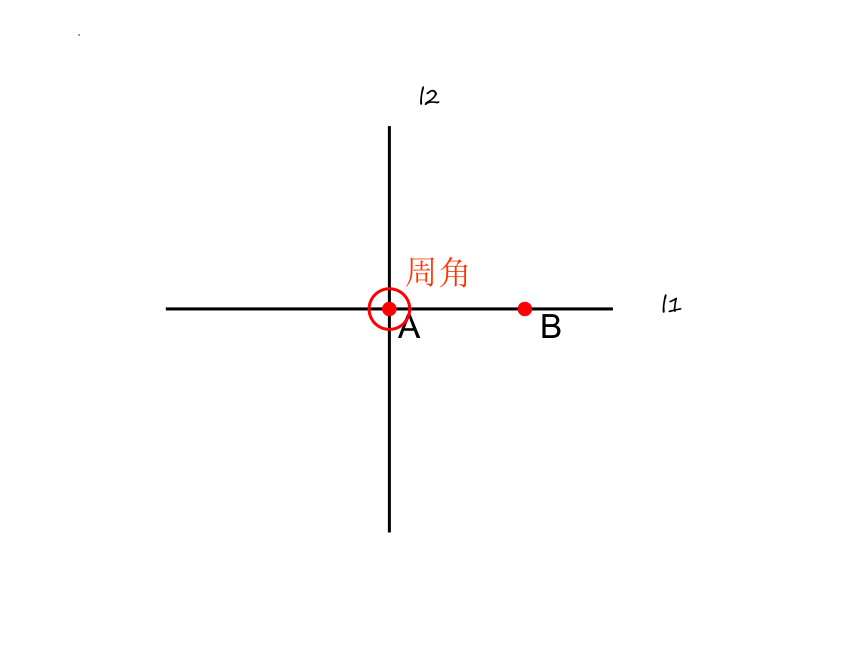
l1
l2
A
B
周角
B
A
l2
l1
l1
l2
A
B
1
l1
l2
A
B
l3
相交
同一平面内两条直线的位置关系
永不相交
成90°
→平行
⒈垂线:
提问:怎样的两条直线互相垂直?
⑴在作业本上画出一组垂线。在一条已知直线
上能画几条垂线。
⑵过直线上一点或直线外一点各能画几条直线
与已知直线垂直?试一试。
三、垂线和平行线。
不成90°
垂直
⒉平行线:
提问:怎样的两条直线互相平行?
⑴在作业本上画一组平行线。
⑵在一条已知直线上能画几条平行线?过已知
直线外一点呢?
⑶怎样判断同一平面内两条直线互相垂直还是
互相平行?
位置关系 交点 图例
互相平行
相交
互相垂直
没有交点
有一个交点
有一个交点
叫垂足
说一说生活中见到的垂直或平行的线段。
什么是距离?
请画出点A到这条直线的距离。
A .
线外一点到直线的连线中( )最短。两条平行线之间的距离( )。
垂直线段
处处相等
A
B
A
B
C
A
B
l2
l1
A
B
1
l1
l2
A
B
1
l1
l2
顶点
边
边
角是从一个( )引发的两条( )所组成的图形。
角是从一个(顶点)引发的两条( 射线 )所组成的图形。
A
B
1
l1
l2
2
A
B
1
l1
l2
2
4
3
二、角。
⑴角:从一点引出两条射线,就组成了一个角。
⑵角的特征:
角的大小与两条边叉开的大小有关,与边的
长短无关。
( )
( )
( )
顶点
边
边
90°
45°
45°
90°
60°
30°
⑶角的度量:
计量角大小的单位是什么 怎样用符号表示
⑷角的分类。
名称
图形
特征
小于90°
等于90°
大于90而
小于180 °
等于180°
等于360°
角 ∠
度 65°
锐角
直角
钝角
平角
周角
⌒
综 合 练 习
⒈判断下面的说法是否正确。
⑴ 一条线段向一端无限延长,就是一条射线;向
两端无限延长,就是一条直线。………… ( )
⑵ 线段是直线的一部分。…………………( )
⑶ 不相交的两条直线叫做平行线。…… ( )
⑷ 角的两条边画的越短,这个角就越小。 ( )
⑸ 两条直线互相垂直,相交的角是90°。 ( )
⑹ 小于90°的角是锐角。……………… ( )
⑺ 大于90°的角是钝角。……………… ( )
⑻ 不平行的两条线一定相交。………… ( )
√
√
×
×
√
√
×
×
二、填空。
⑴ 在一条直线上有三个点,那么直线上有( )条
线段,( )条射线。
⑵ 用放大1000倍的放大镜看40°的角,这个角是
( )度。
⑶ 平角的 是( )度,周角的 是( )度。
⑷ 从9时到10时,分针旋转了( )度,时针旋转
了( )度。
⑸如右图:
∠1=( )度
∠2=( )度
60°
1
2
你是怎样理解“点无大小,线有长短”这句话的?
(点移动形成线)
从A到B有三条路,人们为什么会选择走中间的直路?
两点之间,线段最短。
综合练习
1. 从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线( )的线段。
2. 下图中,∠1=( )度,∠2=( )度。
60
150
垂直
3. 一个三角形中,最小的角是46°,按角分类,这个三角形是( )三角形。
4.经过两点可以画出( )条直线;两条直线相交有( )个交点。
5.同一平面内,两条直线会出现( )( )等位置关系,在平面图形中作高一般要用到( )关系
锐角
一
一
相交
平行
垂直
(二)选择题。
1. 在同一平面内,画已知直线的垂线,可以画( )。
A. 1条 B. 4条 C. 2条 D. 无数条
2. 用100倍的放大镜看40°的角,这个角的度数是( )度。
A. 4 B. 40 C. 400 D. 4000
A
B
D
(三)判断题。
1. 一条射线长12米。 ( )
2.两条直线相交,一定有两个交点。 ( )
3.小于180°的角是钝角。 ( )
4.角的两条边画得越短,这个角就越小。 ( )
5.用一副三角板可以拼成105°的角。 ( )
×
√
×
×
×
课外练习
1、看图填空:
①.图中有____条直线。
②.图中以A点为端点的射线有____条。
③.图中有____条线段。
2、操作练习:
使图1增加2个直角。
使图2增加3个直角。
使图3增加4个直角。
1 2 3
求下列图形中角1 的度数。
40度
这是一个等腰三角形,图中角1的
度数是多少
1
)
求下列图形中角1 的度数。
60度
这是一个等腰梯形,图中角1的
度数是多少
1
)
求下列图形中∠ 1 的度数。
图中∠1: ∠ 2: ∠ 3= 3:2:5。
1
)
2
3
线与角
“五线”——直线、射线、线段、垂线、平行线;
“五角”——锐角、直角、钝角、平角、周角。
A
A
B
A
B
A
B
线段
名称 图 形 联 系 区 别
射线
直线
⑴都是直的
⑵线段是射
线或直线的
一部分
有两个端点
有一个端点
没有端点
①线段、射线和直线的长度有限吗?为什么?
②过一点能画几条直线?几条射线?
③过两点能几条直线?直线上两点之间的部分是什么?
一、线段、射线和直线。
要把一根细木条固定在墙上,至少要几枚钉子?为什么?
小知识,大学问。
l1
l2
A
B
1
3
l1
l2
A
B
平角
l1
l2
A
B
周角
B
A
l2
l1
l1
l2
A
B
1
l1
l2
A
B
l3
相交
同一平面内两条直线的位置关系
永不相交
成90°
→平行
⒈垂线:
提问:怎样的两条直线互相垂直?
⑴在作业本上画出一组垂线。在一条已知直线
上能画几条垂线。
⑵过直线上一点或直线外一点各能画几条直线
与已知直线垂直?试一试。
三、垂线和平行线。
不成90°
垂直
⒉平行线:
提问:怎样的两条直线互相平行?
⑴在作业本上画一组平行线。
⑵在一条已知直线上能画几条平行线?过已知
直线外一点呢?
⑶怎样判断同一平面内两条直线互相垂直还是
互相平行?
位置关系 交点 图例
互相平行
相交
互相垂直
没有交点
有一个交点
有一个交点
叫垂足
说一说生活中见到的垂直或平行的线段。
什么是距离?
请画出点A到这条直线的距离。
A .
线外一点到直线的连线中( )最短。两条平行线之间的距离( )。
垂直线段
处处相等
A
B
A
B
C
A
B
l2
l1
A
B
1
l1
l2
A
B
1
l1
l2
顶点
边
边
角是从一个( )引发的两条( )所组成的图形。
角是从一个(顶点)引发的两条( 射线 )所组成的图形。
A
B
1
l1
l2
2
A
B
1
l1
l2
2
4
3
二、角。
⑴角:从一点引出两条射线,就组成了一个角。
⑵角的特征:
角的大小与两条边叉开的大小有关,与边的
长短无关。
( )
( )
( )
顶点
边
边
90°
45°
45°
90°
60°
30°
⑶角的度量:
计量角大小的单位是什么 怎样用符号表示
⑷角的分类。
名称
图形
特征
小于90°
等于90°
大于90而
小于180 °
等于180°
等于360°
角 ∠
度 65°
锐角
直角
钝角
平角
周角
⌒
综 合 练 习
⒈判断下面的说法是否正确。
⑴ 一条线段向一端无限延长,就是一条射线;向
两端无限延长,就是一条直线。………… ( )
⑵ 线段是直线的一部分。…………………( )
⑶ 不相交的两条直线叫做平行线。…… ( )
⑷ 角的两条边画的越短,这个角就越小。 ( )
⑸ 两条直线互相垂直,相交的角是90°。 ( )
⑹ 小于90°的角是锐角。……………… ( )
⑺ 大于90°的角是钝角。……………… ( )
⑻ 不平行的两条线一定相交。………… ( )
√
√
×
×
√
√
×
×
二、填空。
⑴ 在一条直线上有三个点,那么直线上有( )条
线段,( )条射线。
⑵ 用放大1000倍的放大镜看40°的角,这个角是
( )度。
⑶ 平角的 是( )度,周角的 是( )度。
⑷ 从9时到10时,分针旋转了( )度,时针旋转
了( )度。
⑸如右图:
∠1=( )度
∠2=( )度
60°
1
2
你是怎样理解“点无大小,线有长短”这句话的?
(点移动形成线)
从A到B有三条路,人们为什么会选择走中间的直路?
两点之间,线段最短。
综合练习
1. 从直线外一点到这条直线可以画无数条线段,其中最短的是和这条直线( )的线段。
2. 下图中,∠1=( )度,∠2=( )度。
60
150
垂直
3. 一个三角形中,最小的角是46°,按角分类,这个三角形是( )三角形。
4.经过两点可以画出( )条直线;两条直线相交有( )个交点。
5.同一平面内,两条直线会出现( )( )等位置关系,在平面图形中作高一般要用到( )关系
锐角
一
一
相交
平行
垂直
(二)选择题。
1. 在同一平面内,画已知直线的垂线,可以画( )。
A. 1条 B. 4条 C. 2条 D. 无数条
2. 用100倍的放大镜看40°的角,这个角的度数是( )度。
A. 4 B. 40 C. 400 D. 4000
A
B
D
(三)判断题。
1. 一条射线长12米。 ( )
2.两条直线相交,一定有两个交点。 ( )
3.小于180°的角是钝角。 ( )
4.角的两条边画得越短,这个角就越小。 ( )
5.用一副三角板可以拼成105°的角。 ( )
×
√
×
×
×
课外练习
1、看图填空:
①.图中有____条直线。
②.图中以A点为端点的射线有____条。
③.图中有____条线段。
2、操作练习:
使图1增加2个直角。
使图2增加3个直角。
使图3增加4个直角。
1 2 3
求下列图形中角1 的度数。
40度
这是一个等腰三角形,图中角1的
度数是多少
1
)
求下列图形中角1 的度数。
60度
这是一个等腰梯形,图中角1的
度数是多少
1
)
求下列图形中∠ 1 的度数。
图中∠1: ∠ 2: ∠ 3= 3:2:5。
1
)
2
3
