六年级下册数学苏教版第5课时 立体图形课件(共19张PPT)
文档属性
| 名称 | 六年级下册数学苏教版第5课时 立体图形课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 12:07:21 | ||
图片预览



文档简介
(共19张PPT)
空间与图形——
图形的认识 测量
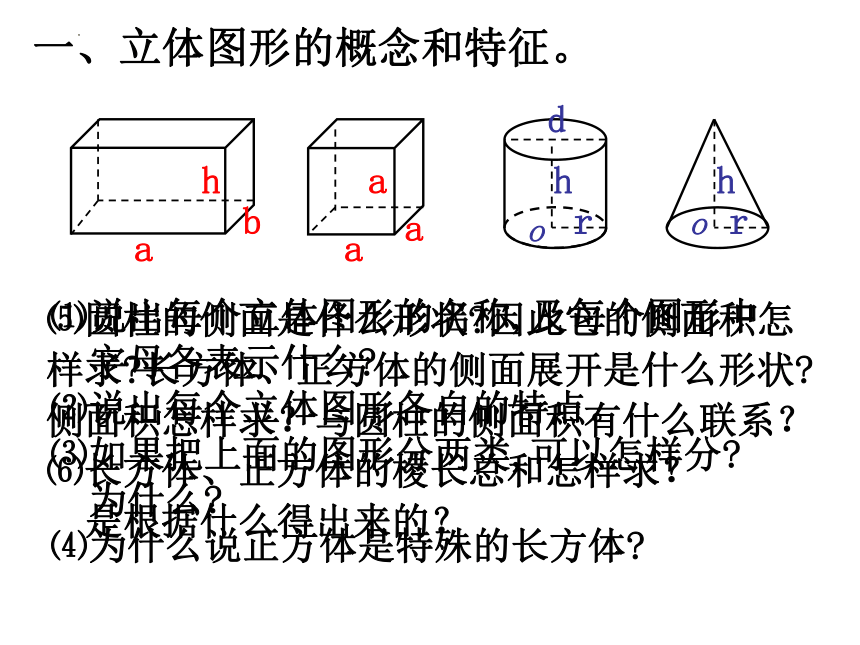
一、立体图形的概念和特征。
a
b
h
a
a
a
o
r
h
d
o
r
h
⑴说出每个立体图形的名称,及每个图形中
字母各表示什么
⑵说出每个立体图形各自的特点。
⑶如果把上面的图形分两类,可以怎样分
为什么
⑷为什么说正方体是特殊的长方体
⑸圆柱的侧面是什么形状 因此它的侧面积怎样求 长方体、正方体的侧面展开是什么形状
侧面积怎样求?与圆柱的侧面积有什么联系?
⑹长方体、正方体的棱长总和怎样求?
是根据什么得出来的?
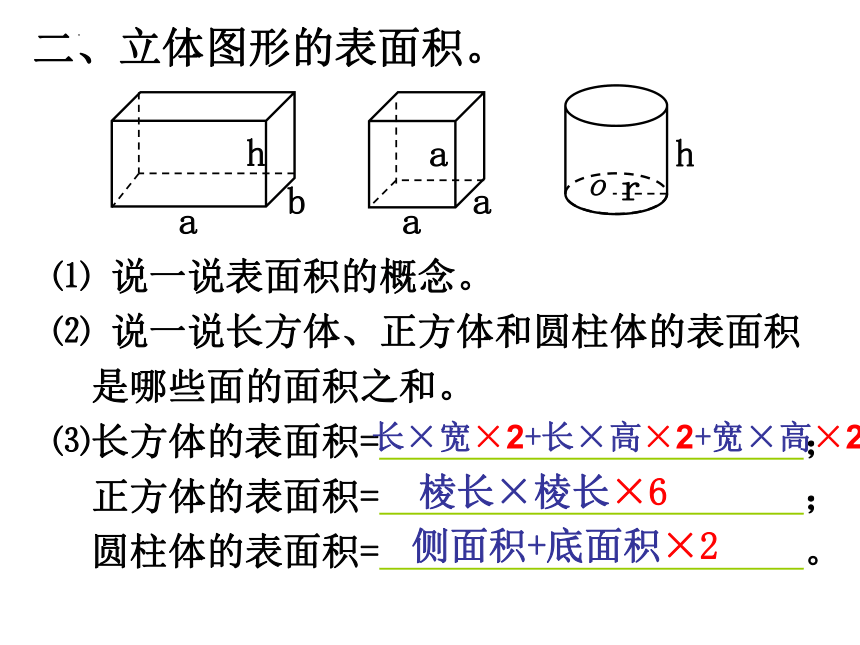
二、立体图形的表面积。
a
b
h
a
a
a
o
h
r
⑴ 说一说表面积的概念。
⑵ 说一说长方体、正方体和圆柱体的表面积
是哪些面的面积之和。
⑶长方体的表面积= ;
正方体的表面积= ;
圆柱体的表面积= 。
长×宽×2+长×高×2+宽×高×2
棱长×棱长×6
侧面积+底面积×2
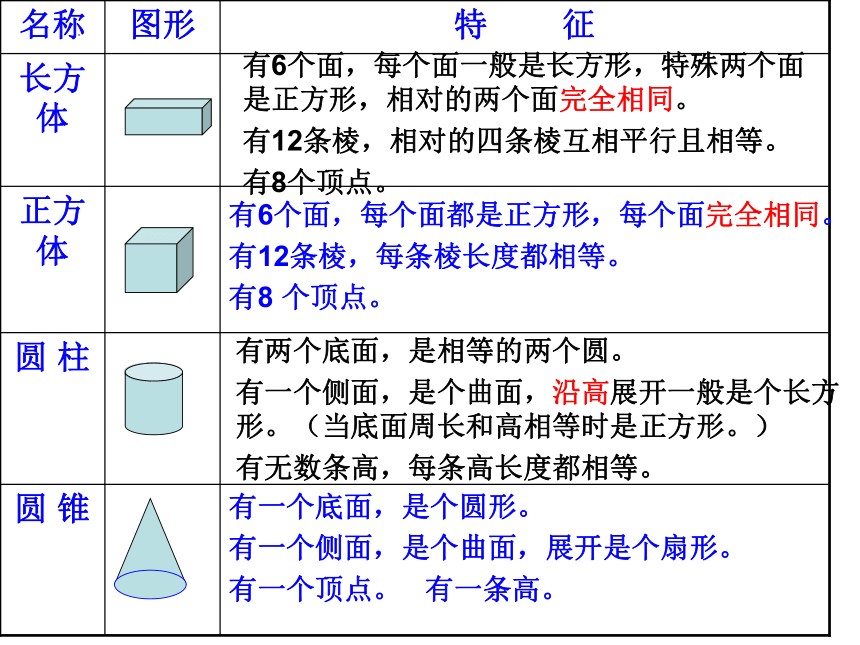
名称 图形 特 征
长方体
正方体
圆 柱
圆 锥
有6个面,每个面一般是长方形,特殊两个面是正方形,相对的两个面完全相同。
有12条棱,相对的四条棱互相平行且相等。
有8个顶点。
有6个面,每个面都是正方形,每个面完全相同。
有12条棱,每条棱长度都相等。
有8 个顶点。
有两个底面,是相等的两个圆。
有一个侧面,是个曲面,沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
有无数条高,每条高长度都相等。
有一个底面,是个圆形。
有一个侧面,是个曲面,展开是个扇形。
有一个顶点。 有一条高。
(1)圆柱的上下两个面是( ) 的两个圆,叫做圆柱的( )。还有一个曲面,叫做圆柱的( )。圆柱的( )叫做圆柱的高,它有( )高。
(2)圆锥的底面是( ),侧面是一个( ),从( )到( )的距离是圆锥的高,它只有( )高。
完全相同
底面
侧面
两个底面之间的距离
无数条
一个圆
曲面
顶点
底面圆心
一条
练习一、认真思考,慎重判断:
① 圆柱的侧面展开一定是长方形。 ( )
②这面小旗旋转一周产生的图形是圆锥体。( )
③ 一根长24厘米的铁丝制作成一个正方体框架,
棱长是3厘米。 ( )
√
×
×
3厘米
4厘米
5cm
2cm
3cm
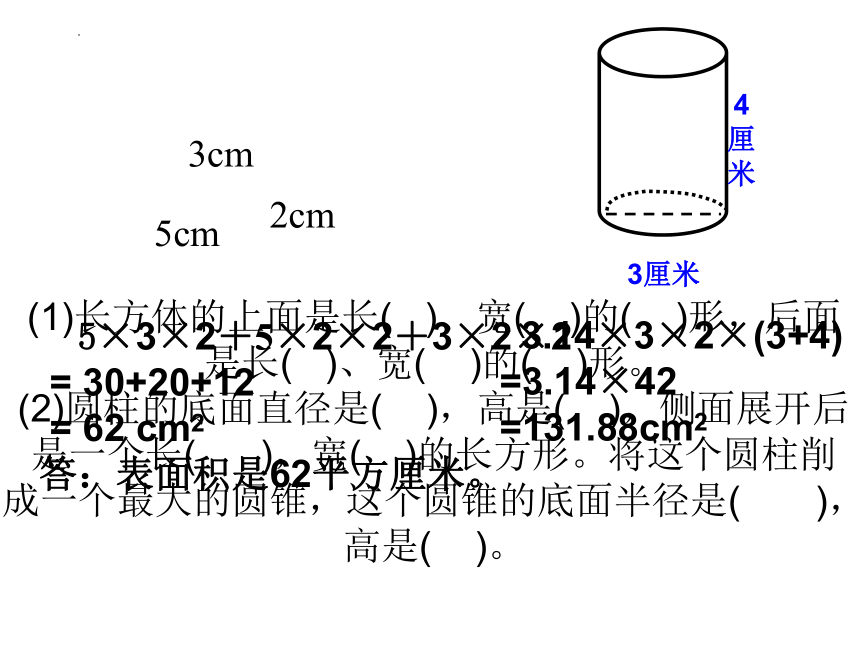
5×3×2+5×2×2+3×2×2
= 30+20+12
= 62 cm2
答:表面积是62平方厘米。
3.14×3×2×(3+4)
=3.14×42
=131.88cm2
(1)长方体的上面是长( )、宽( )的( )形,后面是长( )、宽( )的( )形。
(2)圆柱的底面直径是( ),高是( ),侧面展开后是一个长( ),宽( )的长方形。将这个圆柱削成一个最大的圆锥,这个圆锥的底面半径是( ),高是( )。
1、选择正确答案的序号填在括号内。
(1)下图中,以直线为轴旋转一周,可以形成圆柱的是……………………( )
A. B. C. D.
(2)下列图形中,不能折成正方体的图形是( )
A. B. C. D.
C
A
2、判断:
(1)圆柱的侧面沿高展开后可能是长方形,也可能是正方形。 ( )
(2)圆柱的高只有一条。 ( )
(3)底面积和高都相等的长方体、正方体和圆柱,体积也相等。 ( )
×
√
√
在下面的方格纸上画出左边圆柱的展开图。(每个方格边长1厘米)
底面直径为7厘米,高为12厘米.将24罐这种饮料按图方式放入箱内,这个箱子的长、宽、高至少是多少
如图是一个长方体的展开图,这个长方体的长、宽、高分别是多少厘米?
6厘米
16厘米
8厘米
1一块长方形铁皮长30厘米、宽25厘米,
从四个角切掉边长为5厘米的正方形,做
成铁盒。这个铁盒的表面积是多少?
2右图是一个边长为4厘米
的正方体,分别在前后、
左右、上下各面的中心
位置挖去一个棱长为1厘米
的正方体,做成一种玩具。
它的表面积是多少平方厘米?
空间与图形——
图形的认识 测量
一、立体图形的概念和特征。
a
b
h
a
a
a
o
r
h
d
o
r
h
⑴说出每个立体图形的名称,及每个图形中
字母各表示什么
⑵说出每个立体图形各自的特点。
⑶如果把上面的图形分两类,可以怎样分
为什么
⑷为什么说正方体是特殊的长方体
⑸圆柱的侧面是什么形状 因此它的侧面积怎样求 长方体、正方体的侧面展开是什么形状
侧面积怎样求?与圆柱的侧面积有什么联系?
⑹长方体、正方体的棱长总和怎样求?
是根据什么得出来的?
二、立体图形的表面积。
a
b
h
a
a
a
o
h
r
⑴ 说一说表面积的概念。
⑵ 说一说长方体、正方体和圆柱体的表面积
是哪些面的面积之和。
⑶长方体的表面积= ;
正方体的表面积= ;
圆柱体的表面积= 。
长×宽×2+长×高×2+宽×高×2
棱长×棱长×6
侧面积+底面积×2
名称 图形 特 征
长方体
正方体
圆 柱
圆 锥
有6个面,每个面一般是长方形,特殊两个面是正方形,相对的两个面完全相同。
有12条棱,相对的四条棱互相平行且相等。
有8个顶点。
有6个面,每个面都是正方形,每个面完全相同。
有12条棱,每条棱长度都相等。
有8 个顶点。
有两个底面,是相等的两个圆。
有一个侧面,是个曲面,沿高展开一般是个长方形。(当底面周长和高相等时是正方形。)
有无数条高,每条高长度都相等。
有一个底面,是个圆形。
有一个侧面,是个曲面,展开是个扇形。
有一个顶点。 有一条高。
(1)圆柱的上下两个面是( ) 的两个圆,叫做圆柱的( )。还有一个曲面,叫做圆柱的( )。圆柱的( )叫做圆柱的高,它有( )高。
(2)圆锥的底面是( ),侧面是一个( ),从( )到( )的距离是圆锥的高,它只有( )高。
完全相同
底面
侧面
两个底面之间的距离
无数条
一个圆
曲面
顶点
底面圆心
一条
练习一、认真思考,慎重判断:
① 圆柱的侧面展开一定是长方形。 ( )
②这面小旗旋转一周产生的图形是圆锥体。( )
③ 一根长24厘米的铁丝制作成一个正方体框架,
棱长是3厘米。 ( )
√
×
×
3厘米
4厘米
5cm
2cm
3cm
5×3×2+5×2×2+3×2×2
= 30+20+12
= 62 cm2
答:表面积是62平方厘米。
3.14×3×2×(3+4)
=3.14×42
=131.88cm2
(1)长方体的上面是长( )、宽( )的( )形,后面是长( )、宽( )的( )形。
(2)圆柱的底面直径是( ),高是( ),侧面展开后是一个长( ),宽( )的长方形。将这个圆柱削成一个最大的圆锥,这个圆锥的底面半径是( ),高是( )。
1、选择正确答案的序号填在括号内。
(1)下图中,以直线为轴旋转一周,可以形成圆柱的是……………………( )
A. B. C. D.
(2)下列图形中,不能折成正方体的图形是( )
A. B. C. D.
C
A
2、判断:
(1)圆柱的侧面沿高展开后可能是长方形,也可能是正方形。 ( )
(2)圆柱的高只有一条。 ( )
(3)底面积和高都相等的长方体、正方体和圆柱,体积也相等。 ( )
×
√
√
在下面的方格纸上画出左边圆柱的展开图。(每个方格边长1厘米)
底面直径为7厘米,高为12厘米.将24罐这种饮料按图方式放入箱内,这个箱子的长、宽、高至少是多少
如图是一个长方体的展开图,这个长方体的长、宽、高分别是多少厘米?
6厘米
16厘米
8厘米
1一块长方形铁皮长30厘米、宽25厘米,
从四个角切掉边长为5厘米的正方形,做
成铁盒。这个铁盒的表面积是多少?
2右图是一个边长为4厘米
的正方体,分别在前后、
左右、上下各面的中心
位置挖去一个棱长为1厘米
的正方体,做成一种玩具。
它的表面积是多少平方厘米?
