六年级下册数学苏教版第3课时 因数和倍数课件(共36张PPT)
文档属性
| 名称 | 六年级下册数学苏教版第3课时 因数和倍数课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 152.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 12:10:41 | ||
图片预览








文档简介
(共36张PPT)
因数和倍数
找出与众不同的数:1、2、3、4、7、9。
我认为 与众不同,
因为 。
什么是因数?什么是倍数?
如果a×b=c(a、b为非0自然数),
那么我们可以说:
a、b是c的因数 ,c是a、b的倍数 。
6是18的因数,18是6的倍数 。
用6和18举例
能不能说18是倍数,6是因数?
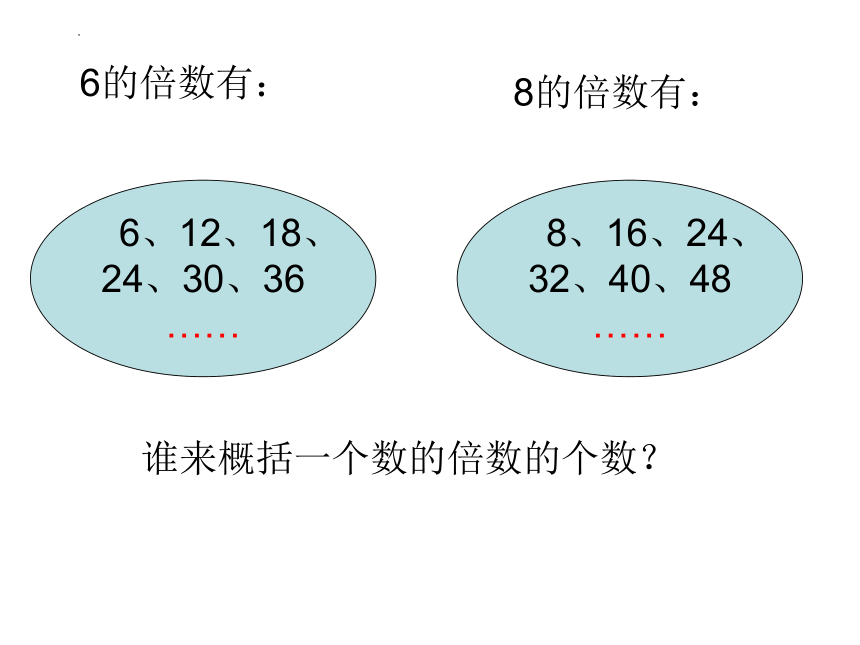
6、12、18、
24、30、36
……
6的倍数有:
8的倍数有:
8、16、24、
32、40、48
……
谁来概括一个数的倍数的个数?
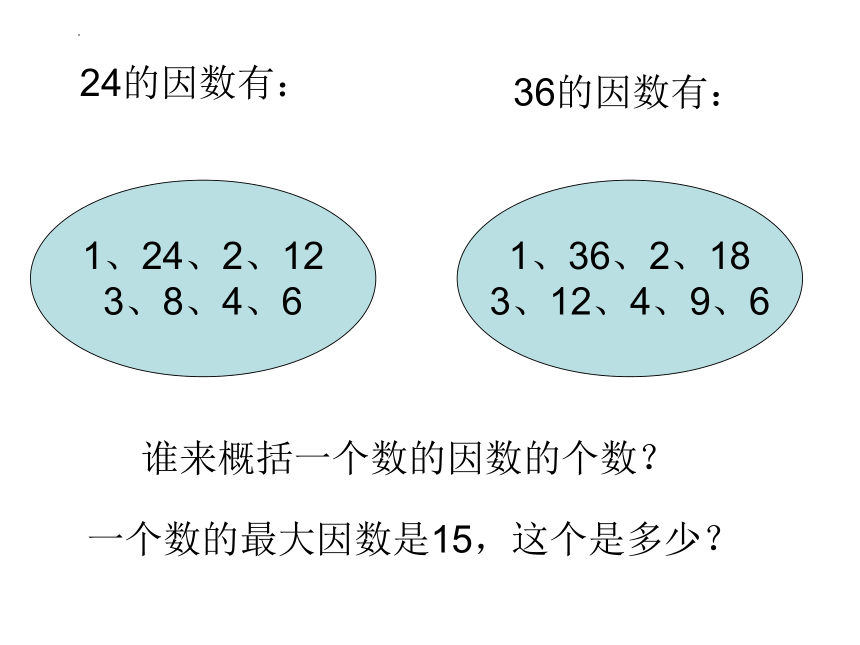
1、24、2、12
3、8、4、6
24的因数有:
36的因数有:
1、36、2、18
3、12、4、9、6
谁来概括一个数的因数的个数?
一个数的最大因数是15,这个是多少?
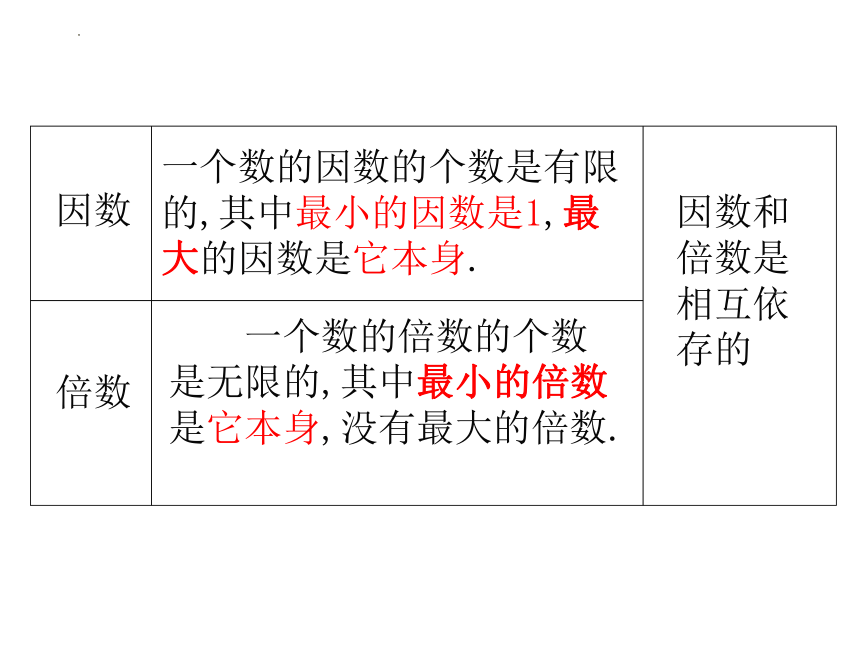
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身.
一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数.
因数和倍数是相互依存的
因数
倍数
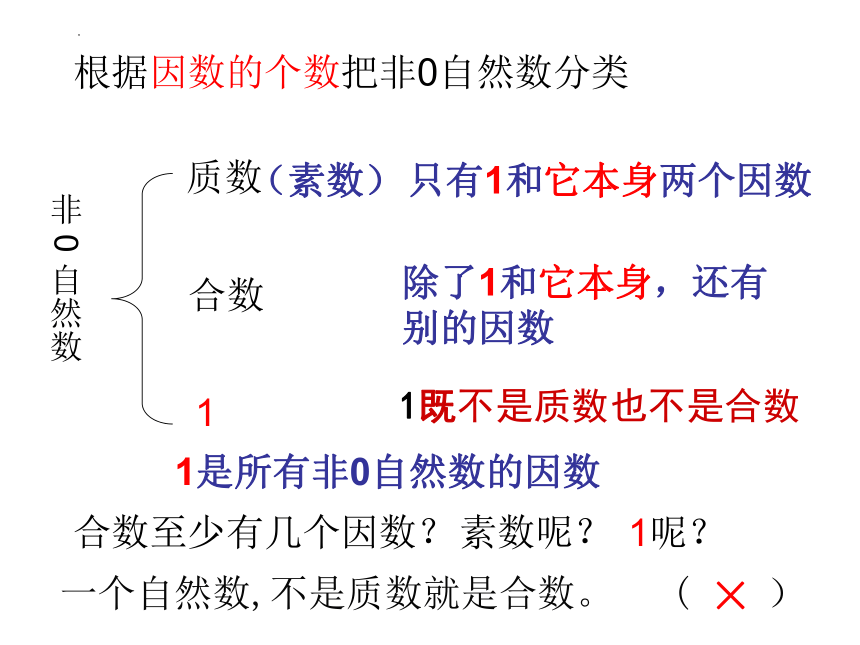
根据因数的个数把非0自然数分类
质数
合数
1
非 0 自然数
(素数)
只有1和它本身两个因数
除了1和它本身,还有
别的因数
1是所有非0自然数的因数
合数至少有几个因数?
素数呢?
1呢?
一个自然数,不是质数就是合数。 ( )
×
1既不是质数也不是合数
最小的质数是:
最小的合数是:
2
4
下列哪些数是质数?哪些数是合数?
质数有:
合数有:
17
41
2
4
39
51
91
9
50以内的质数有哪些?
2、3、5、7、11、13、17、19、23、
29、31、37、41、43、47
2、3、5、7、11、13、17、19、23、
29、31、37、41、43、47
自然数按是不是2的倍数来分为哪两类?
偶数
奇数
自然数
个位上是0、2、4、6、8
个位上是1、3、5、7、9
分别有什么特征?
2的倍数的特征:
个位上是0、2、4、6、8
5的倍数的特征:
个位上是0或5
3的倍数的特征:
各位上的数的和是3的倍数
各位上的数的和是3的倍数
9的倍数的特征呢?4呢?
能同时被2,5整除的数的特征:
个位是0
能同时被2,3,5整除的数的特征:
个位是0,而且各个位上的
数字的和能被3整除。
注意:有一些数能被7,9,11,13整除,但是不容易看出来,这是大家在约分中容易忽略的。
偶数和奇数
一个自然数,不是奇数就是偶数
偶数±偶数=( )
奇数±奇数=( )
偶数±奇数=( )
偶数×偶数=( )
奇数×奇数=( )
偶数×奇数=( )
偶数
偶数
偶数
偶数
奇数
奇数
最小的偶数是:
最小的奇数是:
0
1
123是不是3的倍数?
571是不是3的倍数?
至少加上几?
减去几呢?
你的学号是不是2、3、5的倍数呢?
与同桌交流。
奇数:
偶数:
质数:
合数:
在1—20这些数中: (1既不是素数,也不是合数)
1、3、5、7、9、11、13、15、17、19
2、4、6、8、10、12、14、16、18、20
2、3、5、7、11、13、17、19。
(共8个,和为77。)
4、6、8、9、10、12、14、15、16、18、20。
(共11个,和为132。)
最小的奇数是
最小的偶数是
最小的合数是
最小的质数是
1
0
4
2
1、24、2、12
3、8、4、6
24的因数有:
36的因数有:
1、36、2、18
3、12、4、9、6
24的因数有:
36的因数有:
1、2、
3、4、
6、12
9、
18、
36
8、24
1、2、
3、4、
6、12
什么叫最大公因数?
24和36的最大公因数是12,
12 是24和36的最大公因数
(36,24)=12
24和36的公因数
6、12、18、
24、30、36
……
6的倍数有:
8的倍数有:
8、16、24、
32、40、48
……
6的倍数有:
8的倍数有:
6、12、18、30、36、42、
……
24、
48、
……
8、16、32、40、56、64、
……
6和8的
公倍数
24、
48、
……
什么叫最小公倍数?
6和8的最小公倍数是24
24是6和8的最小公倍数
[6,8]=24
说说下面各组数的最大公因数和最小公倍数。
最大公因数 最小公倍数
5和7
( 5 ,7 )=1
[ 5, 7 ]=35
9和10
( 9,10)=1
[ 9,10 ]=90
1和20
( 1,20)=1
[ 1,20 ]=20
当两个数互质时,
它们的最大公因数是1,
最小公倍数是它们的乘积。
任意的两个素数,
1和任意自然数,
连续的两个自然数,
2和任意奇数
互质
如果a和b是互质数,那么a和b的最大公因数是 ,最小公倍数是 。
1
ab
说说下面各组数的最大公因数和最小公倍数。
最大公因数 最小公倍数
4和28
( 4,28 )=4
[ 4,28 ]=28
7和91
( 7,91)=7
[ 7,91 ]=91
17和51
( 17,51)=17
[ 17,51 ]=51
16和32
( 16,32 )=16
[ 16,32 ]=32
当两个数存在倍数关系时,
较小数是它们的最大公因数
较大数是它们的最小公倍数。
如果a是b的倍数,那么a和b的最大公因数是 ,最小公倍数是 。
b
a
如果a是b的倍数,那么a和b的最大公因数是 ,最小公倍数是 。
a÷b=c(a,b,c≠0)
a=4b
……
质因数:
分解质因数:
每一个合数都可以写成几个质数相乘的形式,这几个质数叫做这个合数的质因数。
把一个合数写成几个质因数相乘的形式的过程叫做分解质因数.
分解质因数的方法:短除法
30
2
15
3
5
30=2×3×5
把30分解质因数正确的做法
是( )
A.30=1×2 ×3 ×5
B.2 ×3 ×5=30
C.30=2×3×5
C
1不是质数
书写格式不符
把30分解质因数
⑶.短除法
求24和36的最大公约数和最小公倍数
24 36
2
12
18
2
6
9
3
2
3
24和36的最大公约数是:2×2×3=12
24和36的最小公倍数是: 2×2×3×2×3=72
商互质
除数相乘
所有的除数和商相乘
除数
说说下面各组数的最大公因数和最小公倍数。
最大公因数 最小公倍数
9和15
( 9,15 )=3
[ 9,15 ]=45
16和24
(16,24 )=8
[ 16,24 ]=48
短除法
列举法
一、填空题:
1、写出每组数的最小公倍数[6,4]=12。
2和10 5和8
8和9 10和4
2、写出每组数的最大公因数。(3,5)=1
7和10 12和24
27和3 9和12
[2,10]=10
[5,8]=40
[8,9]=72
[10,4]=20
(7,10)=1
(12,24)=12
(27,3)=3
(9,12)=3
3、填一填:
30的因数有:
45的因数有:
1、3、
5、15
9、
45
2、10、
6、30
30和45的公因数
9的倍数有:
12的倍数有:
9、18、27、45、54、63、
……
12、24、48、60、84、96、
……
9和12的
公倍数
36、
72、
……
二、判断题:
1、因为10÷5=2,所以5是因数,10是倍数。 ( )
2、743的个位上是3,所以743是3的倍数。 ( )
3、任何自然数,它的最大因数和最小倍数都是
它本身。 ( )
4、任何一个自然数至少有两个因数。 ( )
5、1是所有非零自然数的公因数。 ( )
6、个位上是0的数一定是2和5的公倍数。 ( )
7、相邻的两个自然数没有最大公因数。 ( )
8、所有的奇数都是素数,所有的偶数都是合数。 ( )
9、一个最简分数的分子与分母一定是互质数。 ( )
10、两个自然数的积一定是合数。 ( )
√
√
×
×
×
×
×
×
×
√
三、选择题:
1、下面的数,因数个数最多的是( )。
①18 ②36 ③71
2、一个数,它既是12的倍数,又是12的因数,
这个数是( )。
①12 ②24 ③144
3、一筐苹果,2个一拿,3个一拿,5个一拿都
正好拿完,这筐苹果最少应有( )。
①90个 ②30个 ③60个
4、两个奇数的和是( ),两个质数的和是( )。
①偶数 ②奇数 ③奇数或偶数
5、自然数按因数的个数来分,可以分为( )。
①奇数和偶数 ②质数和合数
③质数、合数和1
②
①
②
③
①
③
6、在1、3、5、25这四个数中,最大公因数
为1的有( )对。
①3 ②4 ③5
7、如果甲数÷乙数= 3 (甲、乙是非0自然数),
那么甲、乙两个数的最大公因数是( )。
①3 ②甲数 ③乙数
8、一个合数的因数至少有( )个。
① 2 ② 3 ③ 3个以上
9、24是4和6的( )。
① 公因数 ②公倍数 ③最小公倍数
10、从323中至少减去( )才是3的倍数。
①减去20 ②减去2 ③减去1
③
③
②
②
②
四、综合练习:
1、两根小棒分别长20分米,28分米,要把它们都截成同样长的小棒,且没有剩余,每根小棒最长多少分米?一共可以截成多少段?
4、用长8厘米、宽6厘米的长方形去拼一个正方形,至少需要多少个这样的长方形?
(20,28)=4
20÷4=5(段)
28÷4=7(段)
5+7=12(段)
答:每根小棒长4分米,一共可以截成12段。
[8,6]=24
24÷8=3(个)
24÷6=4(行)
3×4=12(个)
答:至少需要12个这样的长方形。
2、六(1)班学生进行队列表演,每行12人或16人都正好整行,你知道这个班可能有多少人吗?
3、在长40厘米、宽32厘米的长方形纸上裁出同样大小、面积最大的正方形,并且没有剩余,一共可以裁出多少个这样的正方形?
[12,16]=48
答:这个班可能有48人。
(40,32)=8
40÷8=5(个)
32÷8=4(行)
4×5=20(个)
答:至少需要20个这样的长方形。
五、课后练习。
(一)、填空题:
1、在26和78、24和10两组数中,( )是( )的因数,( )是( )的倍数。
2、在自然数中,最小的偶数是( ),最小的奇数是( ),最小的合数是( ),最小的素数是( )。
3、20以内既是偶数又是素数的数是( ),既是奇数又是合数的数是( )。
4、18和12的公因数有( ),最大公因数是( )。4和9的公倍数有( ),最小公倍数是( )。
0
1
4
2
2
9和15
1、2、3、6
6
36、72……
36
将1、2、3、5按要求组成一个两位数。
1、素数:
2、偶数:
3、5的倍数:
4、有因数3:
5、2和3的公倍数:
6、3和5的公倍数:
13、23、31、53
12、32、52
15、25、35
12、15、21、51
12
15
6、从36的因数中选择四个数可以组成比例( )。
1×36=2×18
4×9=3×12
1:2=18:36
4:3=12:9
1:3=12:36
1×36=3×12
4×9=6×6
4:6=6:9
(二)、选择题:
1、10和4的最小公倍数是( ),最大公因数是( )。
①10、4 ②40、1 ③20、2
2、对分母为20和8的两个分数通分,用( )作公分母比较合适。
①20 ②40 ③160
3、把15、20的因数、公因数填在下面的图中,中间区域填写的数是( )
①1、3、5、15 ②1、2、4、5、20
③1、5
15的因数
20的因数
15和20的公因数
③
②
③
三、综合运用:
1、小明和小军去图书馆借书,小明每6天去一次,小军每8天去一次,4月30日两人同时去了图书馆,几月几日他们又再次相遇?
2、把46块奶糖和38块水果糖分别平均分给一个组的同学,结果奶糖剩1块,水果糖剩3块,你知道这个组最多有几位同学吗?
[6,8]=24
答:5月24日他们再次相遇。
(45,35)=5
答:这个小组最多5人。
46-1=45 (块)
38-3=35 (块)
因数和倍数
找出与众不同的数:1、2、3、4、7、9。
我认为 与众不同,
因为 。
什么是因数?什么是倍数?
如果a×b=c(a、b为非0自然数),
那么我们可以说:
a、b是c的因数 ,c是a、b的倍数 。
6是18的因数,18是6的倍数 。
用6和18举例
能不能说18是倍数,6是因数?
6、12、18、
24、30、36
……
6的倍数有:
8的倍数有:
8、16、24、
32、40、48
……
谁来概括一个数的倍数的个数?
1、24、2、12
3、8、4、6
24的因数有:
36的因数有:
1、36、2、18
3、12、4、9、6
谁来概括一个数的因数的个数?
一个数的最大因数是15,这个是多少?
一个数的因数的个数是有限的,其中最小的因数是1,最大的因数是它本身.
一个数的倍数的个数是无限的,其中最小的倍数是它本身,没有最大的倍数.
因数和倍数是相互依存的
因数
倍数
根据因数的个数把非0自然数分类
质数
合数
1
非 0 自然数
(素数)
只有1和它本身两个因数
除了1和它本身,还有
别的因数
1是所有非0自然数的因数
合数至少有几个因数?
素数呢?
1呢?
一个自然数,不是质数就是合数。 ( )
×
1既不是质数也不是合数
最小的质数是:
最小的合数是:
2
4
下列哪些数是质数?哪些数是合数?
质数有:
合数有:
17
41
2
4
39
51
91
9
50以内的质数有哪些?
2、3、5、7、11、13、17、19、23、
29、31、37、41、43、47
2、3、5、7、11、13、17、19、23、
29、31、37、41、43、47
自然数按是不是2的倍数来分为哪两类?
偶数
奇数
自然数
个位上是0、2、4、6、8
个位上是1、3、5、7、9
分别有什么特征?
2的倍数的特征:
个位上是0、2、4、6、8
5的倍数的特征:
个位上是0或5
3的倍数的特征:
各位上的数的和是3的倍数
各位上的数的和是3的倍数
9的倍数的特征呢?4呢?
能同时被2,5整除的数的特征:
个位是0
能同时被2,3,5整除的数的特征:
个位是0,而且各个位上的
数字的和能被3整除。
注意:有一些数能被7,9,11,13整除,但是不容易看出来,这是大家在约分中容易忽略的。
偶数和奇数
一个自然数,不是奇数就是偶数
偶数±偶数=( )
奇数±奇数=( )
偶数±奇数=( )
偶数×偶数=( )
奇数×奇数=( )
偶数×奇数=( )
偶数
偶数
偶数
偶数
奇数
奇数
最小的偶数是:
最小的奇数是:
0
1
123是不是3的倍数?
571是不是3的倍数?
至少加上几?
减去几呢?
你的学号是不是2、3、5的倍数呢?
与同桌交流。
奇数:
偶数:
质数:
合数:
在1—20这些数中: (1既不是素数,也不是合数)
1、3、5、7、9、11、13、15、17、19
2、4、6、8、10、12、14、16、18、20
2、3、5、7、11、13、17、19。
(共8个,和为77。)
4、6、8、9、10、12、14、15、16、18、20。
(共11个,和为132。)
最小的奇数是
最小的偶数是
最小的合数是
最小的质数是
1
0
4
2
1、24、2、12
3、8、4、6
24的因数有:
36的因数有:
1、36、2、18
3、12、4、9、6
24的因数有:
36的因数有:
1、2、
3、4、
6、12
9、
18、
36
8、24
1、2、
3、4、
6、12
什么叫最大公因数?
24和36的最大公因数是12,
12 是24和36的最大公因数
(36,24)=12
24和36的公因数
6、12、18、
24、30、36
……
6的倍数有:
8的倍数有:
8、16、24、
32、40、48
……
6的倍数有:
8的倍数有:
6、12、18、30、36、42、
……
24、
48、
……
8、16、32、40、56、64、
……
6和8的
公倍数
24、
48、
……
什么叫最小公倍数?
6和8的最小公倍数是24
24是6和8的最小公倍数
[6,8]=24
说说下面各组数的最大公因数和最小公倍数。
最大公因数 最小公倍数
5和7
( 5 ,7 )=1
[ 5, 7 ]=35
9和10
( 9,10)=1
[ 9,10 ]=90
1和20
( 1,20)=1
[ 1,20 ]=20
当两个数互质时,
它们的最大公因数是1,
最小公倍数是它们的乘积。
任意的两个素数,
1和任意自然数,
连续的两个自然数,
2和任意奇数
互质
如果a和b是互质数,那么a和b的最大公因数是 ,最小公倍数是 。
1
ab
说说下面各组数的最大公因数和最小公倍数。
最大公因数 最小公倍数
4和28
( 4,28 )=4
[ 4,28 ]=28
7和91
( 7,91)=7
[ 7,91 ]=91
17和51
( 17,51)=17
[ 17,51 ]=51
16和32
( 16,32 )=16
[ 16,32 ]=32
当两个数存在倍数关系时,
较小数是它们的最大公因数
较大数是它们的最小公倍数。
如果a是b的倍数,那么a和b的最大公因数是 ,最小公倍数是 。
b
a
如果a是b的倍数,那么a和b的最大公因数是 ,最小公倍数是 。
a÷b=c(a,b,c≠0)
a=4b
……
质因数:
分解质因数:
每一个合数都可以写成几个质数相乘的形式,这几个质数叫做这个合数的质因数。
把一个合数写成几个质因数相乘的形式的过程叫做分解质因数.
分解质因数的方法:短除法
30
2
15
3
5
30=2×3×5
把30分解质因数正确的做法
是( )
A.30=1×2 ×3 ×5
B.2 ×3 ×5=30
C.30=2×3×5
C
1不是质数
书写格式不符
把30分解质因数
⑶.短除法
求24和36的最大公约数和最小公倍数
24 36
2
12
18
2
6
9
3
2
3
24和36的最大公约数是:2×2×3=12
24和36的最小公倍数是: 2×2×3×2×3=72
商互质
除数相乘
所有的除数和商相乘
除数
说说下面各组数的最大公因数和最小公倍数。
最大公因数 最小公倍数
9和15
( 9,15 )=3
[ 9,15 ]=45
16和24
(16,24 )=8
[ 16,24 ]=48
短除法
列举法
一、填空题:
1、写出每组数的最小公倍数[6,4]=12。
2和10 5和8
8和9 10和4
2、写出每组数的最大公因数。(3,5)=1
7和10 12和24
27和3 9和12
[2,10]=10
[5,8]=40
[8,9]=72
[10,4]=20
(7,10)=1
(12,24)=12
(27,3)=3
(9,12)=3
3、填一填:
30的因数有:
45的因数有:
1、3、
5、15
9、
45
2、10、
6、30
30和45的公因数
9的倍数有:
12的倍数有:
9、18、27、45、54、63、
……
12、24、48、60、84、96、
……
9和12的
公倍数
36、
72、
……
二、判断题:
1、因为10÷5=2,所以5是因数,10是倍数。 ( )
2、743的个位上是3,所以743是3的倍数。 ( )
3、任何自然数,它的最大因数和最小倍数都是
它本身。 ( )
4、任何一个自然数至少有两个因数。 ( )
5、1是所有非零自然数的公因数。 ( )
6、个位上是0的数一定是2和5的公倍数。 ( )
7、相邻的两个自然数没有最大公因数。 ( )
8、所有的奇数都是素数,所有的偶数都是合数。 ( )
9、一个最简分数的分子与分母一定是互质数。 ( )
10、两个自然数的积一定是合数。 ( )
√
√
×
×
×
×
×
×
×
√
三、选择题:
1、下面的数,因数个数最多的是( )。
①18 ②36 ③71
2、一个数,它既是12的倍数,又是12的因数,
这个数是( )。
①12 ②24 ③144
3、一筐苹果,2个一拿,3个一拿,5个一拿都
正好拿完,这筐苹果最少应有( )。
①90个 ②30个 ③60个
4、两个奇数的和是( ),两个质数的和是( )。
①偶数 ②奇数 ③奇数或偶数
5、自然数按因数的个数来分,可以分为( )。
①奇数和偶数 ②质数和合数
③质数、合数和1
②
①
②
③
①
③
6、在1、3、5、25这四个数中,最大公因数
为1的有( )对。
①3 ②4 ③5
7、如果甲数÷乙数= 3 (甲、乙是非0自然数),
那么甲、乙两个数的最大公因数是( )。
①3 ②甲数 ③乙数
8、一个合数的因数至少有( )个。
① 2 ② 3 ③ 3个以上
9、24是4和6的( )。
① 公因数 ②公倍数 ③最小公倍数
10、从323中至少减去( )才是3的倍数。
①减去20 ②减去2 ③减去1
③
③
②
②
②
四、综合练习:
1、两根小棒分别长20分米,28分米,要把它们都截成同样长的小棒,且没有剩余,每根小棒最长多少分米?一共可以截成多少段?
4、用长8厘米、宽6厘米的长方形去拼一个正方形,至少需要多少个这样的长方形?
(20,28)=4
20÷4=5(段)
28÷4=7(段)
5+7=12(段)
答:每根小棒长4分米,一共可以截成12段。
[8,6]=24
24÷8=3(个)
24÷6=4(行)
3×4=12(个)
答:至少需要12个这样的长方形。
2、六(1)班学生进行队列表演,每行12人或16人都正好整行,你知道这个班可能有多少人吗?
3、在长40厘米、宽32厘米的长方形纸上裁出同样大小、面积最大的正方形,并且没有剩余,一共可以裁出多少个这样的正方形?
[12,16]=48
答:这个班可能有48人。
(40,32)=8
40÷8=5(个)
32÷8=4(行)
4×5=20(个)
答:至少需要20个这样的长方形。
五、课后练习。
(一)、填空题:
1、在26和78、24和10两组数中,( )是( )的因数,( )是( )的倍数。
2、在自然数中,最小的偶数是( ),最小的奇数是( ),最小的合数是( ),最小的素数是( )。
3、20以内既是偶数又是素数的数是( ),既是奇数又是合数的数是( )。
4、18和12的公因数有( ),最大公因数是( )。4和9的公倍数有( ),最小公倍数是( )。
0
1
4
2
2
9和15
1、2、3、6
6
36、72……
36
将1、2、3、5按要求组成一个两位数。
1、素数:
2、偶数:
3、5的倍数:
4、有因数3:
5、2和3的公倍数:
6、3和5的公倍数:
13、23、31、53
12、32、52
15、25、35
12、15、21、51
12
15
6、从36的因数中选择四个数可以组成比例( )。
1×36=2×18
4×9=3×12
1:2=18:36
4:3=12:9
1:3=12:36
1×36=3×12
4×9=6×6
4:6=6:9
(二)、选择题:
1、10和4的最小公倍数是( ),最大公因数是( )。
①10、4 ②40、1 ③20、2
2、对分母为20和8的两个分数通分,用( )作公分母比较合适。
①20 ②40 ③160
3、把15、20的因数、公因数填在下面的图中,中间区域填写的数是( )
①1、3、5、15 ②1、2、4、5、20
③1、5
15的因数
20的因数
15和20的公因数
③
②
③
三、综合运用:
1、小明和小军去图书馆借书,小明每6天去一次,小军每8天去一次,4月30日两人同时去了图书馆,几月几日他们又再次相遇?
2、把46块奶糖和38块水果糖分别平均分给一个组的同学,结果奶糖剩1块,水果糖剩3块,你知道这个组最多有几位同学吗?
[6,8]=24
答:5月24日他们再次相遇。
(45,35)=5
答:这个小组最多5人。
46-1=45 (块)
38-3=35 (块)
