青岛版数学九年级上册1.4图形的位似 课件(共20张PPT)
文档属性
| 名称 | 青岛版数学九年级上册1.4图形的位似 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 13:51:44 | ||
图片预览




文档简介
(共20张PPT)
1.4 图形的位似
2
情
境
导
学
探
新
知
壹
3
生活发现-------奇妙的位似
放大过程中发生了什么变化?
大小发生了变化---位置改变。
图片形状并未发生改变。
还有什么特点呢?
2022年7月18日,问天实验舱与长征五号B遥三运载火箭组合体已转运至发射区。神州14号员乘组成功开启问天实验舱舱门,顺利进入问天实验舱。这是中国航天员首次在轨进入科学实验舱。
4
合
作
探
究
释
疑
难
贰
5
对称
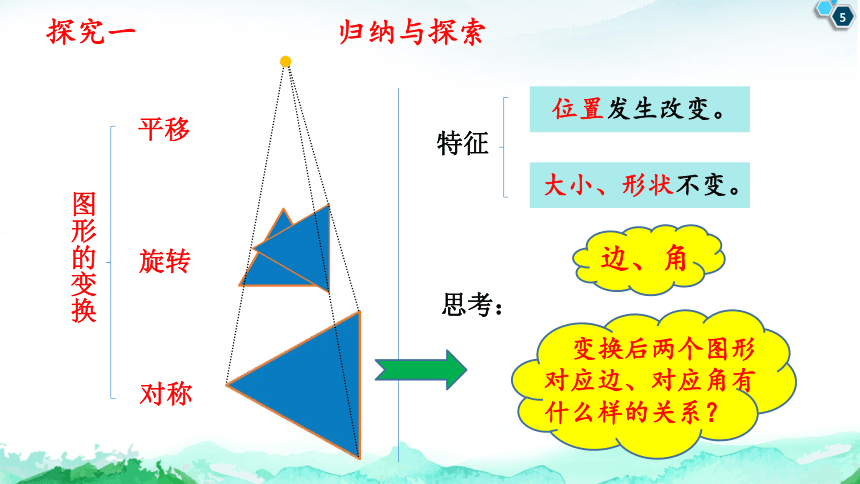
探究一 归纳与探索
图形的变换
旋转
平移
大小、形状不变。
位置发生改变。
特征
思考:
变换后两个图形对应边、对应角有什么样的关系?
边、角
1、对应边有什么样的位置关系和数量关系?
6
探究二 画图与观察
在三角形中,
分别为的中点。
中位线定理
位置:∥
∥
=
=
∥
=
数量:
.
.
.
7
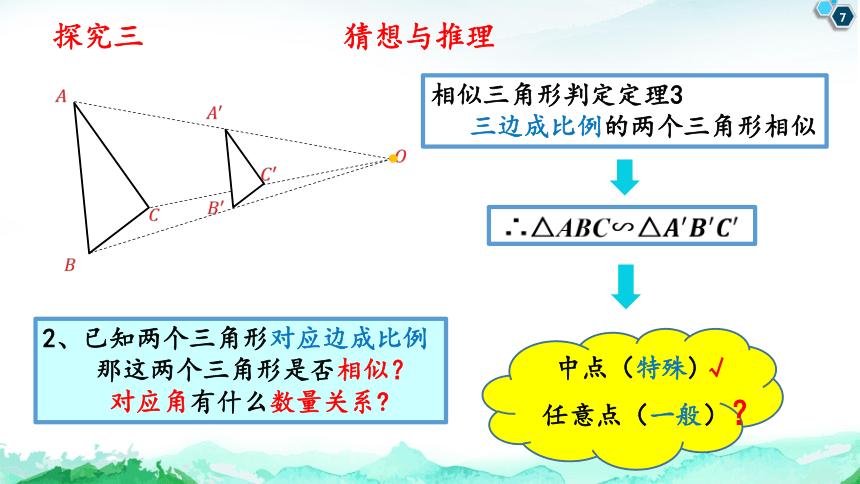
探究三 猜想与推理
2、已知两个三角形对应边成比例
那这两个三角形是否相似?
对应角有什么数量关系
相似三角形判定定理3
三边成比例的两个三角形相似
∴△ABC∽△
中点(特殊)√
任意点(一般)?
8
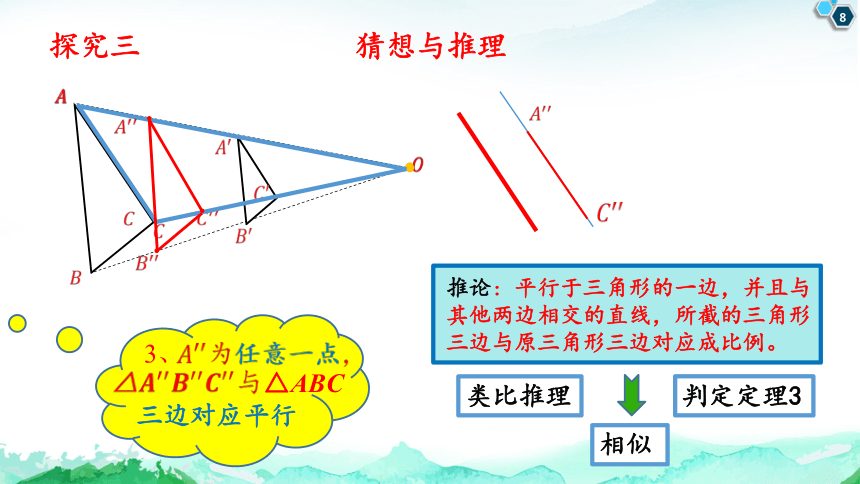
探究三 猜想与推理
为任意一点,
△与
△ABC
三边对应平行
3、
判定定理3
推论:平行于三角形的一边,并且与其他两边相交的直线,所截的三角形三边与原三角形三边对应成比例。
相似
.
.
.
类比推理
定义: 互相 且每对
所在的直线都经过 的两个相似多边形叫做 ,这个点我们叫做
9
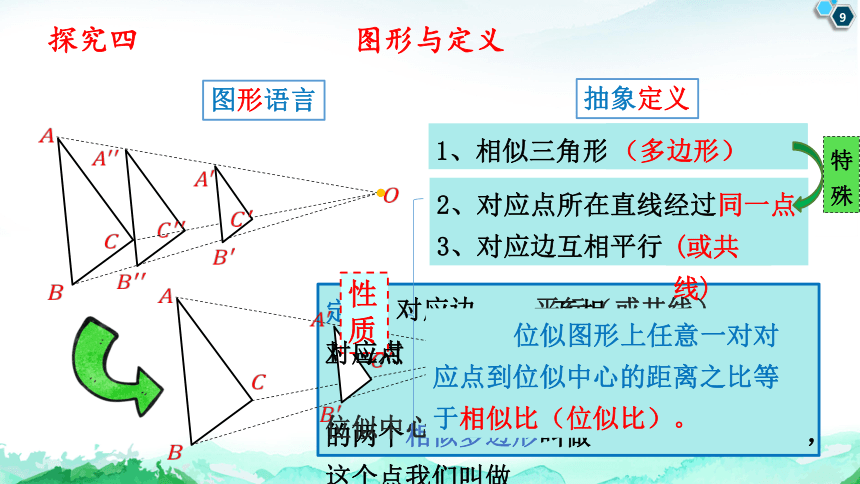
探究四 图形与定义
图形语言
抽象定义
1、相似三角形
(多边形)
性质
2、对应点所在直线经过同一点
3、对应边互相平行
(或共线)
特殊
对应边
平行(或共线)
对应点
同一点
位似图形
位似中心。
位似图形上任意一对对应点到位似中心的距离之比等于相似比(位似比)。
判断如图所示的各图中的两个图形是否是位似图形,
如果是,请指出其位似中心.
10
探究五 判定与思考
定义
判定
位似图形一定是相似图形,相似图形不一定是位似图形。
性质
相似
(同侧)
(异侧)
11
例题 实践与应用
如图,已知△ABC与点O.以点O为位似中心,画出△使它与△ABC是位似图形,并且相似比为3:2.
位似中心 对应点所在直线
如何画?
做射线OA,OB,OC;
在射线OA,OB,OC上分别取点
使O= OA等;
(3) 连接 , .
位似图形的画法:
(1)选点:确定位似中心O;
(2)作射线:以多边形的顶点或位似中心为端点作射线;
(3)定对应点:根据相似比在射线上确定所画图形的顶点;
(4)连线:顺次连接各点。
12
例题 实践与应用
如图,已知△ABC与点O.以点O为位似中心,画出△使它与△ABC是位似图形,并且相似比为3:2.
做事严谨、思维开阔!
如何画?
分类讨论
在相似模型中,我们学习过A字形与X形。
类比相似模型,位似图形画法也有A字形与X形。
13
思考 方法小结
A字形
X形
同A异X
14
拓展 文化与生活
我国的学者-墨翟(墨子)和他的学生,做了世界上第一个小孔成倒像的实验,解释了小孔成倒像的原因,指出了光沿直线进行的性质。蜡烛火焰和像就是位似图形。
用胶片放映电影,调整胶片与镜头的距离可以使图形铺满银幕。
15
课
堂
小
结
提
素
养
叁
16
位似图形
相似图形
对应边互相平行(或共线)
对应点所在直线都经过同一点(位似中心)
核心素养
知识
方法
定义
判定:
位似图形一定是相似图形,
相似图形不一定是位似图形。
性质:
画法:
同A异X
建模抽象
类比
从特殊到一般
严谨
直观想象
分类讨论
17
图形学习---------数学思想
著名数学家华罗庚曾说:
“数缺形时少直觉,
形缺数时难入微,
数形结合百般好,
隔离分家万事休。”
18
课
时
分
层
作
业
肆
19
1、课堂日记:记录本节课的重要概念和所掌握的方法与思想。
3、深入探究:如果将两个位似多边形放在平面直角坐标系中,能否用对应顶点坐标间的关系来描述位似这种几何变换呢。
2、巩固训练:完成课本28页1、2小题。
课后作业
学用相长
恳请各位老师批评指正
1.4 图形的位似
2
情
境
导
学
探
新
知
壹
3
生活发现-------奇妙的位似
放大过程中发生了什么变化?
大小发生了变化---位置改变。
图片形状并未发生改变。
还有什么特点呢?
2022年7月18日,问天实验舱与长征五号B遥三运载火箭组合体已转运至发射区。神州14号员乘组成功开启问天实验舱舱门,顺利进入问天实验舱。这是中国航天员首次在轨进入科学实验舱。
4
合
作
探
究
释
疑
难
贰
5
对称
探究一 归纳与探索
图形的变换
旋转
平移
大小、形状不变。
位置发生改变。
特征
思考:
变换后两个图形对应边、对应角有什么样的关系?
边、角
1、对应边有什么样的位置关系和数量关系?
6
探究二 画图与观察
在三角形中,
分别为的中点。
中位线定理
位置:∥
∥
=
=
∥
=
数量:
.
.
.
7
探究三 猜想与推理
2、已知两个三角形对应边成比例
那这两个三角形是否相似?
对应角有什么数量关系
相似三角形判定定理3
三边成比例的两个三角形相似
∴△ABC∽△
中点(特殊)√
任意点(一般)?
8
探究三 猜想与推理
为任意一点,
△与
△ABC
三边对应平行
3、
判定定理3
推论:平行于三角形的一边,并且与其他两边相交的直线,所截的三角形三边与原三角形三边对应成比例。
相似
.
.
.
类比推理
定义: 互相 且每对
所在的直线都经过 的两个相似多边形叫做 ,这个点我们叫做
9
探究四 图形与定义
图形语言
抽象定义
1、相似三角形
(多边形)
性质
2、对应点所在直线经过同一点
3、对应边互相平行
(或共线)
特殊
对应边
平行(或共线)
对应点
同一点
位似图形
位似中心。
位似图形上任意一对对应点到位似中心的距离之比等于相似比(位似比)。
判断如图所示的各图中的两个图形是否是位似图形,
如果是,请指出其位似中心.
10
探究五 判定与思考
定义
判定
位似图形一定是相似图形,相似图形不一定是位似图形。
性质
相似
(同侧)
(异侧)
11
例题 实践与应用
如图,已知△ABC与点O.以点O为位似中心,画出△使它与△ABC是位似图形,并且相似比为3:2.
位似中心 对应点所在直线
如何画?
做射线OA,OB,OC;
在射线OA,OB,OC上分别取点
使O= OA等;
(3) 连接 , .
位似图形的画法:
(1)选点:确定位似中心O;
(2)作射线:以多边形的顶点或位似中心为端点作射线;
(3)定对应点:根据相似比在射线上确定所画图形的顶点;
(4)连线:顺次连接各点。
12
例题 实践与应用
如图,已知△ABC与点O.以点O为位似中心,画出△使它与△ABC是位似图形,并且相似比为3:2.
做事严谨、思维开阔!
如何画?
分类讨论
在相似模型中,我们学习过A字形与X形。
类比相似模型,位似图形画法也有A字形与X形。
13
思考 方法小结
A字形
X形
同A异X
14
拓展 文化与生活
我国的学者-墨翟(墨子)和他的学生,做了世界上第一个小孔成倒像的实验,解释了小孔成倒像的原因,指出了光沿直线进行的性质。蜡烛火焰和像就是位似图形。
用胶片放映电影,调整胶片与镜头的距离可以使图形铺满银幕。
15
课
堂
小
结
提
素
养
叁
16
位似图形
相似图形
对应边互相平行(或共线)
对应点所在直线都经过同一点(位似中心)
核心素养
知识
方法
定义
判定:
位似图形一定是相似图形,
相似图形不一定是位似图形。
性质:
画法:
同A异X
建模抽象
类比
从特殊到一般
严谨
直观想象
分类讨论
17
图形学习---------数学思想
著名数学家华罗庚曾说:
“数缺形时少直觉,
形缺数时难入微,
数形结合百般好,
隔离分家万事休。”
18
课
时
分
层
作
业
肆
19
1、课堂日记:记录本节课的重要概念和所掌握的方法与思想。
3、深入探究:如果将两个位似多边形放在平面直角坐标系中,能否用对应顶点坐标间的关系来描述位似这种几何变换呢。
2、巩固训练:完成课本28页1、2小题。
课后作业
学用相长
恳请各位老师批评指正
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
