青岛版八年级下册6.1 平行四边形及其性质平行四边形及其性质 课件(共17张PPT)
文档属性
| 名称 | 青岛版八年级下册6.1 平行四边形及其性质平行四边形及其性质 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 13:52:34 | ||
图片预览






文档简介
(共17张PPT)
2.3 简单轴对称图形-等腰三角形
2
情
境
导
学
探
新
知
3
观察与思考
4
合
作
探
究
释
疑
难
5
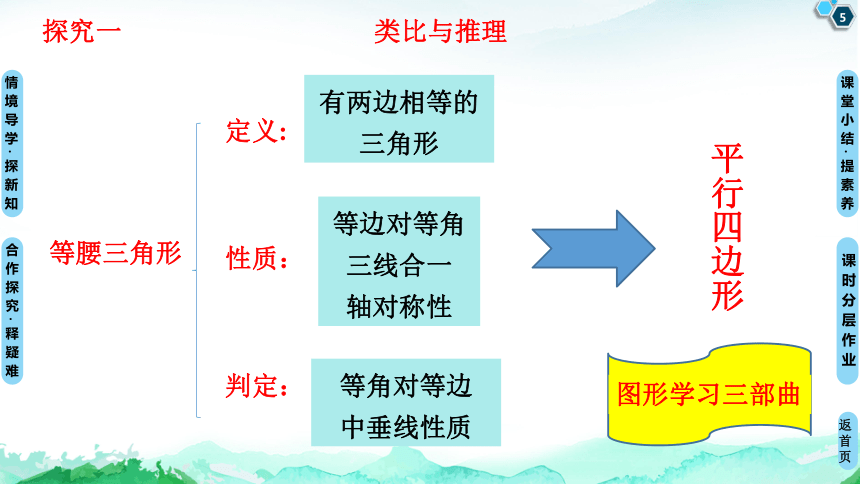
等腰三角形
定义:
性质:
判定:
有两边相等的 三角形
等边对等角
三线合一
轴对称性
等角对等边
中垂线性质
探究一 类比与推理
图形学习三部曲
平行四边形
6
探究二 图形与概念
1、平行四边形的定义:有两组对边分别平行的四边形叫做平行四边形。
下图记作“ ABCD”。
2、表示方法:平行四边形用符号“ ”表示,
B
A
D
C
O
读作“平行四边形ABCD”
对边
重要名称: 对角
对角线
7
探究三 活动与实践
类比研究等腰三角形的方法,我们可以从哪几个方面研究平行四边形的性质?
边与边、角与角
任意画一平行四边形,连接对角线,沿对角线把平行四边形剪成两个三角形,这两个三角形能否重合?
思考
实践
转化的数学 思想方法
8
探究三 活动与实践
平行四边形对边、对角的数量关系。
数学的严谨性
9
证明:如图,连接AC(作辅助线)
∵ 四边形ABCD是平行四边形.
∴ AD∥BC,AB ∥ CD(定义性质)
已知: 四边形ABCD是平行四边形.
求证: AB=CD,BC=DA; ∠B=∠D
逻辑推理
A
D
C
B
1
2
3
4
∴∠1=∠2,同理∠3=∠4。
又AC是△ABC和△CDA的公共边
∴ △ABC≌ △CDA(ASA)
∴AB=CD,BC=DA
∠B=∠D
同理∠BAD=∠DCB
平行四边形的性质:
对边相等
对角相等
做事严谨、行为规范!
10
平行四边形性质定理
定理名称 性质定理1 性质定理2
图形语言
文字语言
符号语言
B
A
D
C
B
A
D
C
三种转换
平行四边形对边相等
平行四边形对角相等
∵ ABCD
∴ AB等于CD
BC等于AD
∵ ABCD
∴ ∠A等于∠C
∠B等于∠D
11
求证:
夹在两条平行直线间的平行线段相等
A
B
C
D
平行
两组对边分别平行
证明:∵AD∥BC
AB∥CD
∴四边形ABCD是平行四边形
(平行四边形定义)
∴AB=CD
(平行四边形性质定理)
例题求证
12
课
堂
小
结
提
素
养
13
平行四边形
平行四边形的定义
平行四边形的性质
两组对边分别平行
对边相等
对角相等
类比
数形结合
逻辑推理
直观想象
转换
知识层面
数学思想方法层面
核心素养层面
著名数学家华罗庚曾说:
“数缺形时少直觉,
形缺数时难入微,
数形结合百般好,
隔离分家万事休。”
数学思想方法
15
课
时
分
层
作
业
16
1、课堂延续:课本例题1第二问:如果两条直线平行,那么一条直线上各点到另一条直线的距离相等。
2、巩固练习:课本课后第6页练习1、2小题。
3、深入探究:我们从对边与对角两个方面来探知平行四边形的性质,那对角线又有怎样的特点呢?除此之外,平行四边形还具有哪些方面的性质呢?
恳请各位老师批评指正
2.3 简单轴对称图形-等腰三角形
2
情
境
导
学
探
新
知
3
观察与思考
4
合
作
探
究
释
疑
难
5
等腰三角形
定义:
性质:
判定:
有两边相等的 三角形
等边对等角
三线合一
轴对称性
等角对等边
中垂线性质
探究一 类比与推理
图形学习三部曲
平行四边形
6
探究二 图形与概念
1、平行四边形的定义:有两组对边分别平行的四边形叫做平行四边形。
下图记作“ ABCD”。
2、表示方法:平行四边形用符号“ ”表示,
B
A
D
C
O
读作“平行四边形ABCD”
对边
重要名称: 对角
对角线
7
探究三 活动与实践
类比研究等腰三角形的方法,我们可以从哪几个方面研究平行四边形的性质?
边与边、角与角
任意画一平行四边形,连接对角线,沿对角线把平行四边形剪成两个三角形,这两个三角形能否重合?
思考
实践
转化的数学 思想方法
8
探究三 活动与实践
平行四边形对边、对角的数量关系。
数学的严谨性
9
证明:如图,连接AC(作辅助线)
∵ 四边形ABCD是平行四边形.
∴ AD∥BC,AB ∥ CD(定义性质)
已知: 四边形ABCD是平行四边形.
求证: AB=CD,BC=DA; ∠B=∠D
逻辑推理
A
D
C
B
1
2
3
4
∴∠1=∠2,同理∠3=∠4。
又AC是△ABC和△CDA的公共边
∴ △ABC≌ △CDA(ASA)
∴AB=CD,BC=DA
∠B=∠D
同理∠BAD=∠DCB
平行四边形的性质:
对边相等
对角相等
做事严谨、行为规范!
10
平行四边形性质定理
定理名称 性质定理1 性质定理2
图形语言
文字语言
符号语言
B
A
D
C
B
A
D
C
三种转换
平行四边形对边相等
平行四边形对角相等
∵ ABCD
∴ AB等于CD
BC等于AD
∵ ABCD
∴ ∠A等于∠C
∠B等于∠D
11
求证:
夹在两条平行直线间的平行线段相等
A
B
C
D
平行
两组对边分别平行
证明:∵AD∥BC
AB∥CD
∴四边形ABCD是平行四边形
(平行四边形定义)
∴AB=CD
(平行四边形性质定理)
例题求证
12
课
堂
小
结
提
素
养
13
平行四边形
平行四边形的定义
平行四边形的性质
两组对边分别平行
对边相等
对角相等
类比
数形结合
逻辑推理
直观想象
转换
知识层面
数学思想方法层面
核心素养层面
著名数学家华罗庚曾说:
“数缺形时少直觉,
形缺数时难入微,
数形结合百般好,
隔离分家万事休。”
数学思想方法
15
课
时
分
层
作
业
16
1、课堂延续:课本例题1第二问:如果两条直线平行,那么一条直线上各点到另一条直线的距离相等。
2、巩固练习:课本课后第6页练习1、2小题。
3、深入探究:我们从对边与对角两个方面来探知平行四边形的性质,那对角线又有怎样的特点呢?除此之外,平行四边形还具有哪些方面的性质呢?
恳请各位老师批评指正
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
