六年级下册数学苏教版第13课时 解决问题的策略课件(共21张PPT)
文档属性
| 名称 | 六年级下册数学苏教版第13课时 解决问题的策略课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 115.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 12:17:09 | ||
图片预览






文档简介
(共21张PPT)
解决问题的策略
一、知识整理:
小学阶段学过的解决问题的策略
有列表 、画图 、枚举(一一列举) 、倒推(倒过来想) 、替换 、假设 、转化
(一)认真思考,正确填空。
1、一种消毒药水,是由某种药粉和水按
1:19的比配成的。这种药水中药粉的浓度是( )%.
2、某市举行小学生足球赛,比赛采用淘汰制。10支队伍参赛需赛( )场才能决出冠军;如果已赛了8场,还留有( )支队伍继续比赛。
5
9
2
3、白兔和黑兔只数的比是3:4,黑兔只数是
白兔的( ),白兔只数是黑兔的( ) ,
白兔只数占总只数的( ) ,黑兔只数与
兔总只数的比是( ):( )。
4 7
4、如图所示,
男生人数是女生的( ) ,
女生人数是男生的( ) ,
女生占总人数的( ) ,
男生与总人数的比是( ):( ) 。
3 7
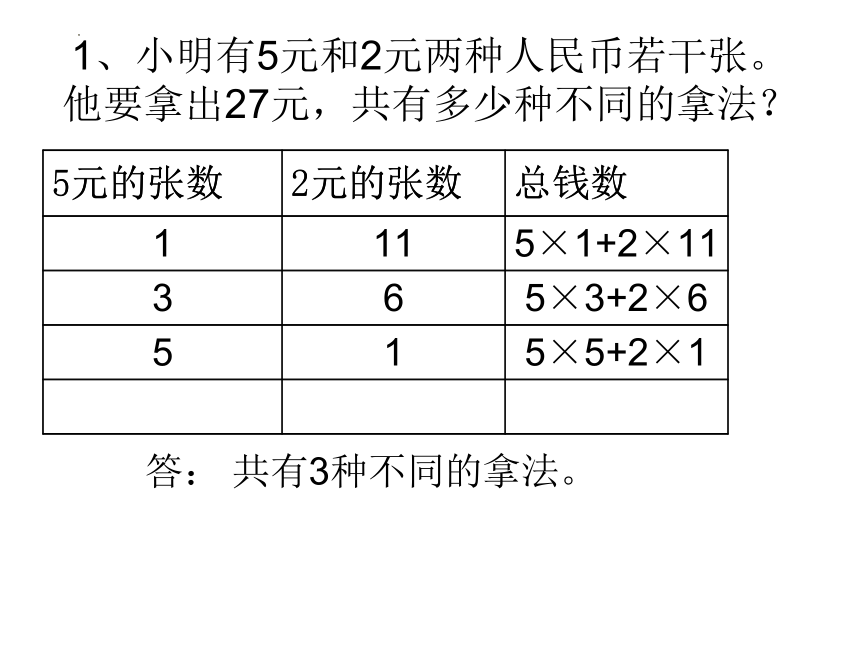
1、小明有5元和2元两种人民币若干张。他要拿出27元,共有多少种不同的拿法?
5元的张数 2元的张数 总钱数
5元的张数 2元的张数 总钱数
1 11 5×1+2×11
3 6 5×3+2×6
5 1 5×5+2×1
答: 共有3种不同的拿法。
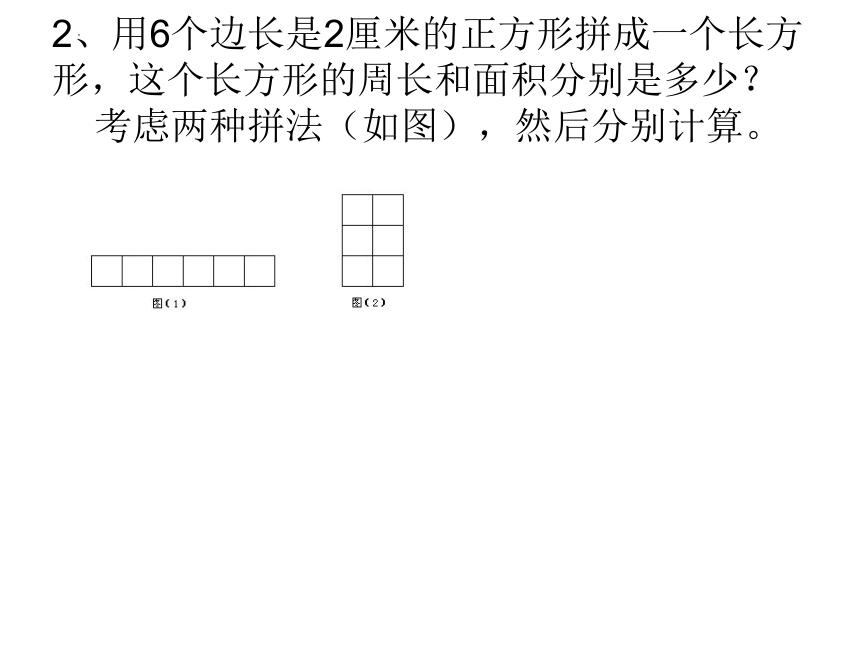
2、用6个边长是2厘米的正方形拼成一个长方形,这个长方形的周长和面积分别是多少?
考虑两种拼法(如图),然后分别计算。
小明问爷爷的年龄,爷爷笑眯眯说:我的年龄减16加上24,再除以3得36,你能计算出我的年龄吗?
4、有5元和10元得人民币共14张,共100元。5元和10元币各有多少张?
解法一:假设14张人民币全是10元的,则共有( )元,比100元多( )元,一张5元替换成10元,多( )元,可以求出5元的人民币有( )张。
解法二:假设14张人民币全是5元的,则共有( )元,比100元少( )元,一张10元替换成5元,少( )元,可以求出10元的人民币有( )张。
140
40
5
8
70
30
5
6
5、甲桶油比乙桶油多3.6千克,甲桶油的 等于乙桶油的 ,那么甲桶原有油多少千克?
甲乙两桶油重量的比是( ):( )。
3.6÷(3-1)=1.8kg
1.8×3=5.4kg
3 1
课外练习
1、一个梯形的下底长20厘米,如果把上底延长6厘米,就变成了长方形,并且面积也会增加24平方厘米,原来梯形的面积是多少平方厘米?
2、物流公司委托小王送1000只玻璃花瓶,双方商定每只运费1角5分,损坏一只不但不计运费,并且要赔偿9角5分。结果,小王共得运费145.6元。你能计算出搬运过程中打破了几只花瓶吗?
打坏一件损失多少元?
3、冬冬看一本儿童故事书,第一天看了 ,第二天看了42页。
这时已看的页数与未看的页数的比是2:3,这本书共有多少页?
4、下图中每个小方格的面积是1平方厘米,阴影部分的面积是多少?
5、下图中,平行四边形的面积是20平方厘米,阴影部分的面积是多少平方厘米?
6、一个正方形,它的边长增加8厘米后,面积就增加了224平方厘米。
(1)画出示意图,并用阴影表示出增加的面积。
(2)小正方形的边长为多少厘米?
课外拓展题
一个圆柱体的侧面积是100平方米,底面半径是4米,求它的体积是多少?
(提示:仔细观察圆柱体切拼成近似长方体的图,你能找到本题最简单的算法。)
2、计算阴影部分的面积:
3、一条公路已经修了它的1/5,再修300米,就能修好这条公路的1/3。这条公路全长多少米?
4、一条公路第一次修了它的1/5,第二次修了300米,这时已经修的和剩下的比为1:2。这条公路全长多少米?
解决问题的策略
一、知识整理:
小学阶段学过的解决问题的策略
有列表 、画图 、枚举(一一列举) 、倒推(倒过来想) 、替换 、假设 、转化
(一)认真思考,正确填空。
1、一种消毒药水,是由某种药粉和水按
1:19的比配成的。这种药水中药粉的浓度是( )%.
2、某市举行小学生足球赛,比赛采用淘汰制。10支队伍参赛需赛( )场才能决出冠军;如果已赛了8场,还留有( )支队伍继续比赛。
5
9
2
3、白兔和黑兔只数的比是3:4,黑兔只数是
白兔的( ),白兔只数是黑兔的( ) ,
白兔只数占总只数的( ) ,黑兔只数与
兔总只数的比是( ):( )。
4 7
4、如图所示,
男生人数是女生的( ) ,
女生人数是男生的( ) ,
女生占总人数的( ) ,
男生与总人数的比是( ):( ) 。
3 7
1、小明有5元和2元两种人民币若干张。他要拿出27元,共有多少种不同的拿法?
5元的张数 2元的张数 总钱数
5元的张数 2元的张数 总钱数
1 11 5×1+2×11
3 6 5×3+2×6
5 1 5×5+2×1
答: 共有3种不同的拿法。
2、用6个边长是2厘米的正方形拼成一个长方形,这个长方形的周长和面积分别是多少?
考虑两种拼法(如图),然后分别计算。
小明问爷爷的年龄,爷爷笑眯眯说:我的年龄减16加上24,再除以3得36,你能计算出我的年龄吗?
4、有5元和10元得人民币共14张,共100元。5元和10元币各有多少张?
解法一:假设14张人民币全是10元的,则共有( )元,比100元多( )元,一张5元替换成10元,多( )元,可以求出5元的人民币有( )张。
解法二:假设14张人民币全是5元的,则共有( )元,比100元少( )元,一张10元替换成5元,少( )元,可以求出10元的人民币有( )张。
140
40
5
8
70
30
5
6
5、甲桶油比乙桶油多3.6千克,甲桶油的 等于乙桶油的 ,那么甲桶原有油多少千克?
甲乙两桶油重量的比是( ):( )。
3.6÷(3-1)=1.8kg
1.8×3=5.4kg
3 1
课外练习
1、一个梯形的下底长20厘米,如果把上底延长6厘米,就变成了长方形,并且面积也会增加24平方厘米,原来梯形的面积是多少平方厘米?
2、物流公司委托小王送1000只玻璃花瓶,双方商定每只运费1角5分,损坏一只不但不计运费,并且要赔偿9角5分。结果,小王共得运费145.6元。你能计算出搬运过程中打破了几只花瓶吗?
打坏一件损失多少元?
3、冬冬看一本儿童故事书,第一天看了 ,第二天看了42页。
这时已看的页数与未看的页数的比是2:3,这本书共有多少页?
4、下图中每个小方格的面积是1平方厘米,阴影部分的面积是多少?
5、下图中,平行四边形的面积是20平方厘米,阴影部分的面积是多少平方厘米?
6、一个正方形,它的边长增加8厘米后,面积就增加了224平方厘米。
(1)画出示意图,并用阴影表示出增加的面积。
(2)小正方形的边长为多少厘米?
课外拓展题
一个圆柱体的侧面积是100平方米,底面半径是4米,求它的体积是多少?
(提示:仔细观察圆柱体切拼成近似长方体的图,你能找到本题最简单的算法。)
2、计算阴影部分的面积:
3、一条公路已经修了它的1/5,再修300米,就能修好这条公路的1/3。这条公路全长多少米?
4、一条公路第一次修了它的1/5,第二次修了300米,这时已经修的和剩下的比为1:2。这条公路全长多少米?
