六年级下册数学苏教版第14课时 式与方程用字母表示数课件(共18张PPT)
文档属性
| 名称 | 六年级下册数学苏教版第14课时 式与方程用字母表示数课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 12:27:12 | ||
图片预览






文档简介
(共18张PPT)
式与方程
用字母表示计算公式
长方形面积=____________________
圆锥体积=______________________
_______________________________
_______________________________
_______________________________
_______________________________
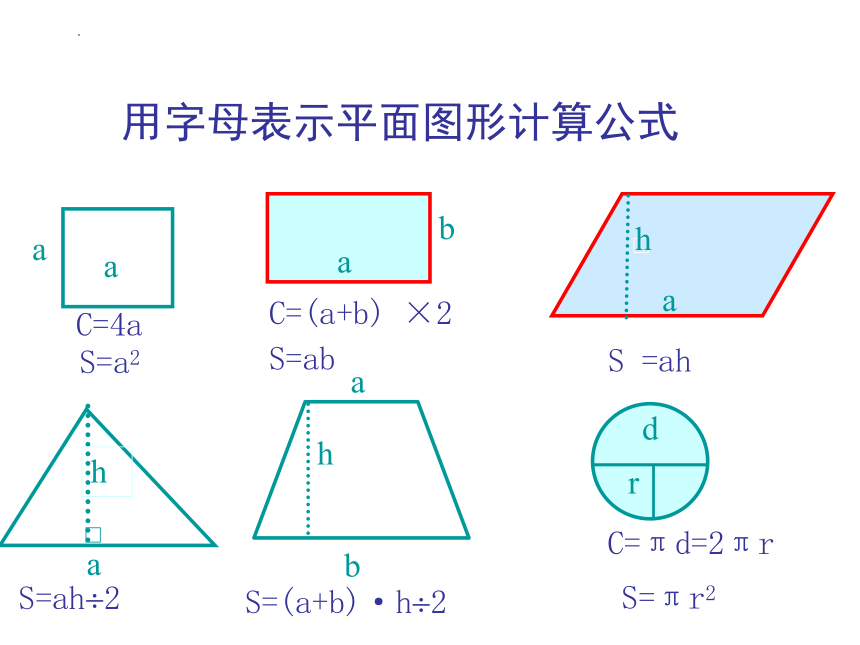
用字母表示平面图形计算公式
a
a
a
h
b
a
h
a
b
a
h
C=4a
S=ah 2
S=(a+b)·h 2
S =ah
S=ab
C=πd=2πr
S=πr2
S=a2
C=(a+b) ×2
d
r
名 称 举 例 用 字 母 表 示
加法 交换律 5+15=15+5
加法 结合律 (8.5+3.26)+5.74 =8.5+(3.26+5.74)
乘法 交换律 8X4=4X8
乘法 结合律 3X1.25X8 =3X(1.25X8)
乘法 分配律 (2.5+1.3)X4 =2.5X4+1.3X4
(1)2a表示___________,
a2表示_____________,
a3表示_____________.
(2) b×5可以简写成______,
b×1可以简写成_______.
x×y可以简写成________.
2个a相加
2个a相乘
3个a相乘
5b
b
xy
基本练习
1.在括号里写出含有字母的式子。
(1)一种贺卡的单价是a元,小英买5张这样的贺卡,用去( )元;小明买n张这样的贺卡,付出10元,应找回( )元。
(2)每千瓦时电费0.52元,每立方米水费2元。小明家本月用了a千瓦时电和b立方米水,一共要付水电费( )元。
5a
10-an
0.52a+2b
(3)3个x相加的和( ) ,3个x相乘的积 ( )。
(4)三个连续自然数,中间数是m,其余两个可以表示为 ( )和( )。
(5)一个圆柱底面半径为r,高为h,它的体积v= ( ) 。
(6)松树高y米,杨树比松树的3/4少5米,杨树高( )米。
(7)斑马有x只,猴子只数是斑马的120%,猴子有( )只,猴子和斑马一共( )只.
3x
x3
1.2x
2.2x
m+1
m-1
2.食堂买来a千克西红柿,每千克 8元;买来3千克黄瓜,每千克b元。
(1)8a表示( )
(2)8a+3b表示( )
(3)8a-3b表示( )
当a=5、b=6时,食堂共付( )元。
(4)请你根据题意写一个用字母表示的式子( ),表示( )
a千克西红柿的价钱
a千克西红柿和3千克黄瓜的总价钱
a千克西红柿比3千克黄瓜多的价钱
58
综合练习
1.用字母表示下列式子
(1)爸爸今年a岁,小华今年b岁,经过c年后,两人相差( )岁。
(2)三个连续的奇数,中间一个是m,另外两个奇数分别是( )和( ),这三个数的和是( )。
a- b
m +2
m - 2
3m
(3)3.小明、小军、小刚三人进行百米赛跑,小明用去x秒,小军比小明多用去2秒,小刚比小明少用0.2秒, ( ) 是冠军,成绩是( )秒。最后一名是( ) ,成绩是( )
(4) 如果 是真分数,a可以是( ) ,
如果是最简真分数,a可以是( )
如果是假分数,a最小是( ) 。
小刚
X-0.2
小军
(X+2)秒
1-11
1、5、7、11
12
2.判断
(1)一个两位数,个位是b,十位是a,这个两位数是ab。 ( )
(2)2a无论什么情况下都不可能等于a2。 ( )
(3)n是偶数,n+1一定是奇数。 ( )
(4)乘法分配律可以用式子(a+b)×c=ac+b来表示。
( )
√
×
×
×
10a+b
a=2 或0
(a+b)×c=ac+bc
3.在○里天上“>”“<”或“=“。
(1)当b=12时,b+19○30,
60-b○32
(2)当x=0.2时,0.6x○0.12,
x÷2○0.2
>
>
=
<
4.解决问题。
某市规定:乘坐出租车起步价为8元(3千米以内),超过3千米以外每1千米按2.5元计费(不足1千米按1千米收费)。小明的妈妈乘坐出租车行了m千米。
(1)用式子表示小明的妈妈应付的钱数。
(2)当m=11时,求小明的妈妈应付多少钱。
8+ (m-3) ×2.5
8+ (11-3) ×2.5
=8+8×2.5
=28(元)
课外练习
一、在( )里写出含有字母的式子。
(1)绿绳长x米,红绳的长度是绿绳的2.4倍,红绳长( )米,两种绳一共长( )米,绿绳比红绳短( )米。
(2)妈妈买8只茶杯,付了100元,找回m元,一只茶杯( )元。
2.4x
3.4x
1.4x
(100 – m) ÷8
(3)师徒加工一批零件,师傅单独完成要a小时,徒弟单独完成要b小时,徒弟和师傅工作时间的比是( ),师傅和徒弟工作效率的比是( )。
(4)m与n的差除以它们的和( )。当m=1.2,n=0.4时,结果是( ).
(5)一个圆锥底面半径为 r,高为h,它的体积v=( )。
(6)分数 如果是真分数,那么x( )y,如果是假分数,那么x( )y.
b:a
b:a
(m-n) ÷(m+n)
0.5
≥
<
二、在○里填“>”、“<”或“=”。
1、当x=1.6时,0.58+0.6x○1.63。
2、当x=0.6时,x+0.3x○55%。
<
<
三、选择。
1、等腰三角形的一个底角是n°,它的顶角是( )°。 A.n° B.90°-n°
C.180°-2n° D.(180°-n°)÷2
2、如果a×75%=b÷3/4= c+0.75,那么a、b、c中最大的是( )。
A.a B.b C.c
3、5个连续偶数,中间的一个数为m,则最大的数是( )。
A.m+1 B.m+2 C.m+3 D.m+4
C
A
D
四、探寻规律。
小明用小棒按照如下方式摆图形。
摆n个八边形需要( )根小棒,141根小棒可摆( )个八边形。
式与方程
用字母表示计算公式
长方形面积=____________________
圆锥体积=______________________
_______________________________
_______________________________
_______________________________
_______________________________
用字母表示平面图形计算公式
a
a
a
h
b
a
h
a
b
a
h
C=4a
S=ah 2
S=(a+b)·h 2
S =ah
S=ab
C=πd=2πr
S=πr2
S=a2
C=(a+b) ×2
d
r
名 称 举 例 用 字 母 表 示
加法 交换律 5+15=15+5
加法 结合律 (8.5+3.26)+5.74 =8.5+(3.26+5.74)
乘法 交换律 8X4=4X8
乘法 结合律 3X1.25X8 =3X(1.25X8)
乘法 分配律 (2.5+1.3)X4 =2.5X4+1.3X4
(1)2a表示___________,
a2表示_____________,
a3表示_____________.
(2) b×5可以简写成______,
b×1可以简写成_______.
x×y可以简写成________.
2个a相加
2个a相乘
3个a相乘
5b
b
xy
基本练习
1.在括号里写出含有字母的式子。
(1)一种贺卡的单价是a元,小英买5张这样的贺卡,用去( )元;小明买n张这样的贺卡,付出10元,应找回( )元。
(2)每千瓦时电费0.52元,每立方米水费2元。小明家本月用了a千瓦时电和b立方米水,一共要付水电费( )元。
5a
10-an
0.52a+2b
(3)3个x相加的和( ) ,3个x相乘的积 ( )。
(4)三个连续自然数,中间数是m,其余两个可以表示为 ( )和( )。
(5)一个圆柱底面半径为r,高为h,它的体积v= ( ) 。
(6)松树高y米,杨树比松树的3/4少5米,杨树高( )米。
(7)斑马有x只,猴子只数是斑马的120%,猴子有( )只,猴子和斑马一共( )只.
3x
x3
1.2x
2.2x
m+1
m-1
2.食堂买来a千克西红柿,每千克 8元;买来3千克黄瓜,每千克b元。
(1)8a表示( )
(2)8a+3b表示( )
(3)8a-3b表示( )
当a=5、b=6时,食堂共付( )元。
(4)请你根据题意写一个用字母表示的式子( ),表示( )
a千克西红柿的价钱
a千克西红柿和3千克黄瓜的总价钱
a千克西红柿比3千克黄瓜多的价钱
58
综合练习
1.用字母表示下列式子
(1)爸爸今年a岁,小华今年b岁,经过c年后,两人相差( )岁。
(2)三个连续的奇数,中间一个是m,另外两个奇数分别是( )和( ),这三个数的和是( )。
a- b
m +2
m - 2
3m
(3)3.小明、小军、小刚三人进行百米赛跑,小明用去x秒,小军比小明多用去2秒,小刚比小明少用0.2秒, ( ) 是冠军,成绩是( )秒。最后一名是( ) ,成绩是( )
(4) 如果 是真分数,a可以是( ) ,
如果是最简真分数,a可以是( )
如果是假分数,a最小是( ) 。
小刚
X-0.2
小军
(X+2)秒
1-11
1、5、7、11
12
2.判断
(1)一个两位数,个位是b,十位是a,这个两位数是ab。 ( )
(2)2a无论什么情况下都不可能等于a2。 ( )
(3)n是偶数,n+1一定是奇数。 ( )
(4)乘法分配律可以用式子(a+b)×c=ac+b来表示。
( )
√
×
×
×
10a+b
a=2 或0
(a+b)×c=ac+bc
3.在○里天上“>”“<”或“=“。
(1)当b=12时,b+19○30,
60-b○32
(2)当x=0.2时,0.6x○0.12,
x÷2○0.2
>
>
=
<
4.解决问题。
某市规定:乘坐出租车起步价为8元(3千米以内),超过3千米以外每1千米按2.5元计费(不足1千米按1千米收费)。小明的妈妈乘坐出租车行了m千米。
(1)用式子表示小明的妈妈应付的钱数。
(2)当m=11时,求小明的妈妈应付多少钱。
8+ (m-3) ×2.5
8+ (11-3) ×2.5
=8+8×2.5
=28(元)
课外练习
一、在( )里写出含有字母的式子。
(1)绿绳长x米,红绳的长度是绿绳的2.4倍,红绳长( )米,两种绳一共长( )米,绿绳比红绳短( )米。
(2)妈妈买8只茶杯,付了100元,找回m元,一只茶杯( )元。
2.4x
3.4x
1.4x
(100 – m) ÷8
(3)师徒加工一批零件,师傅单独完成要a小时,徒弟单独完成要b小时,徒弟和师傅工作时间的比是( ),师傅和徒弟工作效率的比是( )。
(4)m与n的差除以它们的和( )。当m=1.2,n=0.4时,结果是( ).
(5)一个圆锥底面半径为 r,高为h,它的体积v=( )。
(6)分数 如果是真分数,那么x( )y,如果是假分数,那么x( )y.
b:a
b:a
(m-n) ÷(m+n)
0.5
≥
<
二、在○里填“>”、“<”或“=”。
1、当x=1.6时,0.58+0.6x○1.63。
2、当x=0.6时,x+0.3x○55%。
<
<
三、选择。
1、等腰三角形的一个底角是n°,它的顶角是( )°。 A.n° B.90°-n°
C.180°-2n° D.(180°-n°)÷2
2、如果a×75%=b÷3/4= c+0.75,那么a、b、c中最大的是( )。
A.a B.b C.c
3、5个连续偶数,中间的一个数为m,则最大的数是( )。
A.m+1 B.m+2 C.m+3 D.m+4
C
A
D
四、探寻规律。
小明用小棒按照如下方式摆图形。
摆n个八边形需要( )根小棒,141根小棒可摆( )个八边形。
