2023-2024学年人教版数学九年级下册26.2实际问题与反比例函数同步练习(含答案)
文档属性
| 名称 | 2023-2024学年人教版数学九年级下册26.2实际问题与反比例函数同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 385.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 00:00:00 | ||
图片预览



文档简介
26.2实际问题与反比例函数 同步练习
一.选择题(共12小题)
1.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于0.5m3 B.不大于0.5m3
C.不小于0.6m3 D.不大于0.6m3
2.学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温y(℃)与通电时间x(min)成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
A.水温从20℃加热到100℃,需要7min
B.水温下降过程中,y与x的函数关系式是y=
C.上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水
D.在一个加热周期内水温不低于30℃的时间为min
3.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升7℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
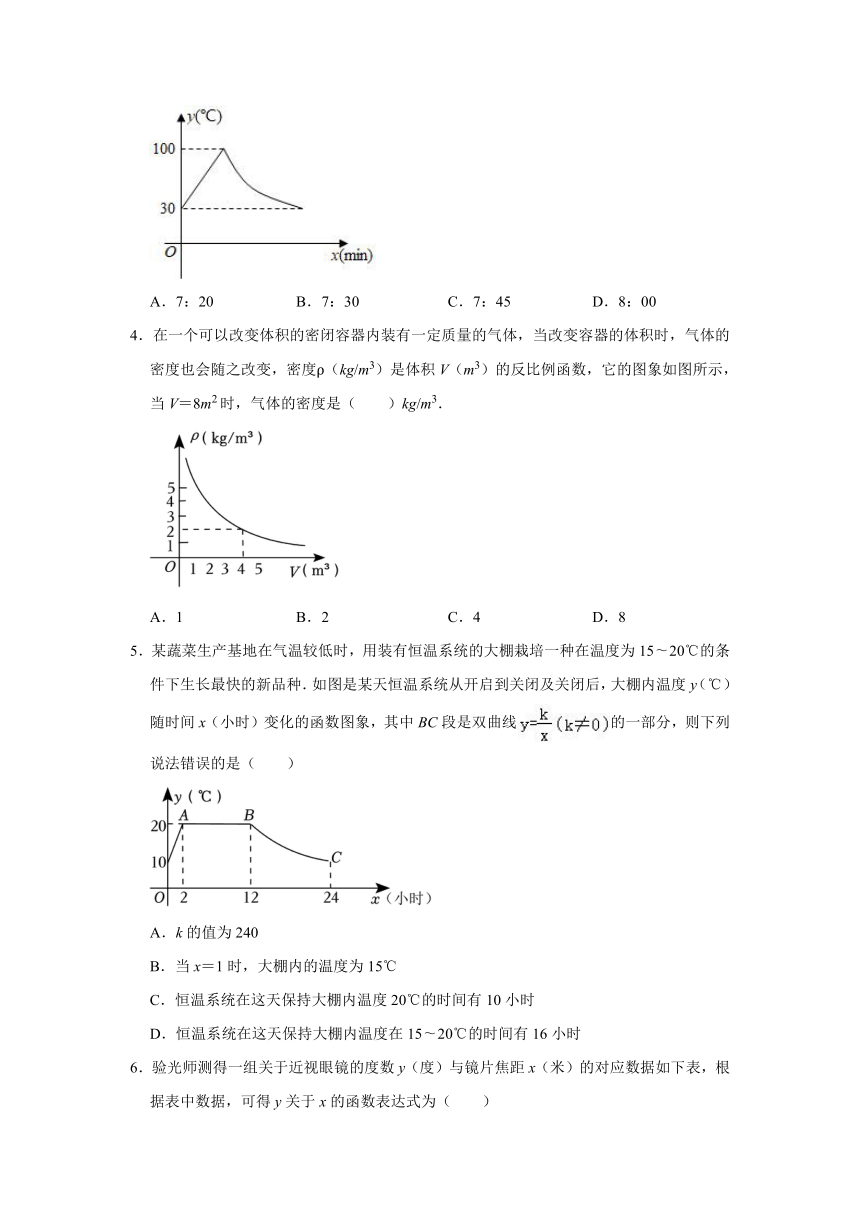
A.7:20 B.7:30 C.7:45 D.8:00
4.在一个可以改变体积的密闭容器内装有一定质量的气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(kg/m3)是体积V(m3)的反比例函数,它的图象如图所示,当V=8m2时,气体的密度是( )kg/m3.
A.1 B.2 C.4 D.8
5.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为15 20℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分,则下列说法错误的是( )
A.k的值为240
B.当x=1时,大棚内的温度为15℃
C.恒温系统在这天保持大棚内温度20℃的时间有10小时
D.恒温系统在这天保持大棚内温度在15 20℃的时间有16小时
6.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
7.小明设计了杠杆平衡实验:如图,取一根长60cm质地均匀的木杆,用细绳绑在木杆的中点O处并将其吊起来,在左侧距离中点O20cm处挂一个重15N的物体,在中点O右侧用一个弹簧测力计竖直向下拉,以保持木杆水平(动力×动力臂=阻力×阻力臂).改变弹簧测力计与中点O的距离L(单位:cm),观察并记录弹簧测力计的示数F(单位:N)有什么变化.小明根据实验得到的下列结论中,不正确的是( )
A.L与F的函数关系式为
B.当L=10时,F=30
C.当L>20时,F>15
D.保持木杆水平,F的最小值为10
8.如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流I(A)与电阻R(Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象可知,下列说法不正确的是( )
A.I与R的函数关系式是
B.当I=0.5时,R=440
C.当R>1000时,I>0.22
D.当880<R<1000时,I的取值范围是0.22<I<0.25
9.某气球充满一定质量的气体后,当温度不变时,气球内的气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积至少为( )
A. B. C. D.
10.如图,一块方砖的三个面A,B,C,其中B面为正方形,A,C两个面为矩形,B面的面积小于A面的面积.若将A,B,C三个面分别向下放在桌面上,则地面所受压强分别为PA,PB,PC,压强的计算公式为,其中P是压强,F是压力(由于方砖的重量不变,故F不变),S是受力面积,则PA,PB,PC的大小关系正确的是( )
A.PA>PB>PC B.PA>PC=PB C.PC=PA>PB D.PB>PA=PC
11.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
A.甲 B.乙 C.丙 D.丁
12.小亮新买了一盏亮度可调节的台灯(图①),他发现调节的原理是当电压一定时,通过调节电阻控制电流的变化从而改变灯光的明暗,台灯的电流I(A)是电阻R(Ω)的反比例函数,其图象如图②所示.下列说法正确的是( )
A.电流I(A)随电阻R(Ω)的增大而增大
B.电流I(A)与电阻R(Ω)的关系式为
C.当电阻R为550Ω时,电流I为0.5A
D.当电阻R≥1100Ω时,电流I的范围为0<I≤0.2A
二.填空题(共5小题)
13.若梯形的下底长为x,上底长为下底长的,高为y,面积为60,则y与x的函数关系式为 .(不考虑x的取值范围)
14.某蓄电池的电压为48V,使用此蓄电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为.当R=6Ω时,I的值为 A.
15.验光师通过检测发现近视眼镜的度数y(度)与镜片焦距x(米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 度.
16.已知蓄电池的电压为定值.使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则蓄电池的电压是 V.
17.科学发现,若气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是关于气体体积V(单位:m3)的反比例函数,如图所示的是恒温下某气球(充满气)的气压与体积的函数图象.当气体体积为2m3时,气压是 kPa.
三.解答题(共5小题)
18.写出函数解析式表示下列关系,并指出它们各是什么函数:
(1)体积是常数V时,圆柱的底面积S与高h的关系;
(2)柳树乡共有耕地面积S(单位:hm2),该乡人均耕地面积y(单位:hm2/人)与全乡总人口x的关系.
19.水塔中储有若干立方米的水,如果每小时放水5m3,那么8小时放完.
(1)求水塔中原有多少立方米的水;
(2)设放水时间为y(h),每小时放水量为x(m3),写出y与x的关系式;
(3)画出(2)中函数的大致图象.
20.某地区上一年度每度电价格为0.8元,年用电量为1亿度,本年度计划将电价调到0.55~0.75元(不包括端点值).经测算,若电价调至x元,则本年度新增用电量y(亿度)与(x﹣0.4)(元)成反比例,且当x=0.65时,y=0.8.
(1)求y与x之间的函数表达式 .
(2)若每度电的成本价为0.3元,当电价调至0.72元时,本年度电力部门的收益是多少元?[收益=用电量×(实际电价﹣成本价)]
21.面积一定的梯形,其上底长是下底长的,设上底长为xcm,高为ycm,且当x=5cm,y=6cm,
(1)求y与x的函数关系式;
(2)求当y=4cm时,下底长多少?
22.一辆汽车准备从甲地开往乙地.若平均速度为80km/h,则需要5h到达.
(1)写出汽车从甲地到乙地所用时间t与平均速度v之间的关系式;
(2)如果准备用8h到达,那么平均速度是多少?
(3)已知汽车的最大平均速度是100km/h,那么汽车最少用多长时间可以到达?
参考答案
一.选择题(共12小题)
1--10CDCAD BCCDD 11--12CD
二.填空题(共5小题)
13.y=
14.8
15.200
16.36
17.100
三.解答题(共5小题)
18.解:(1)由题意可得:S=;
(2)由题意可得:y=.
19.解:(1)5m3×8=40m2,
答:水塔中原有40立方米的水;
(2)∵xy=40,y与x成反比例关系.
∴y与x之间的关系式为y=;
(3)如图所示:
20.解:(1)设y与x之间的函数表达式为 (k≠0).
因为当x=0.65时,y=0.8,所以k=(x﹣0.4)y=(0.65﹣0.4)×0.8=0.2.
所以 即 (0.55<x<0.75).
故答案为: (0.55<x<0.75).
(2)当电价调至0.72元时,本年度新增用电量为 (亿度),则本年度用电量为 1+0.625=1.625(亿度)=1.625×10°(度).
所以( 0.72﹣0.3)×1.625×108=6.825×107 (元).
所以当电价调至0.72元时,本年度电力部门的收益是 6.825×107 元.
21.解:(1)∵x=5cm,y=6cm,上底长是下底长的,
∴下底长为10cm,
∴梯形的面积=(5+10)×6=45,
∵梯形的高=,
∴;
(2)当y=4cm时,x=7.5,
∴2x=15.
答:下底长15cm.
22.解:(1)∵平均速度为80km/h,则需要5h到达,
∴甲地到乙地的距离为80×5=400km,
∴vt=400,
∴汽车从甲地到乙地所用时间t与平均速度v之间的关系式t=;
(2)当t=8时,v==50,
∴平均速度是50km/h;
(3)当v=100时,t==4,
所以汽车最少用4时间可以到达
一.选择题(共12小题)
1.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于0.5m3 B.不大于0.5m3
C.不小于0.6m3 D.不大于0.6m3
2.学校的自动饮水机,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降.此时水温y(℃)与通电时间x(min)成反比例关系.当水温降至20℃时,饮水机再自动加热,若水温在20℃时接通电源,水温y与通电时间x之间的关系如图所示,则下列说法中正确的是( )
A.水温从20℃加热到100℃,需要7min
B.水温下降过程中,y与x的函数关系式是y=
C.上午8点接通电源,可以保证当天9:30能喝到不超过40℃的水
D.在一个加热周期内水温不低于30℃的时间为min
3.教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升7℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20 B.7:30 C.7:45 D.8:00
4.在一个可以改变体积的密闭容器内装有一定质量的气体,当改变容器的体积时,气体的密度也会随之改变,密度ρ(kg/m3)是体积V(m3)的反比例函数,它的图象如图所示,当V=8m2时,气体的密度是( )kg/m3.
A.1 B.2 C.4 D.8
5.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在温度为15 20℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线的一部分,则下列说法错误的是( )
A.k的值为240
B.当x=1时,大棚内的温度为15℃
C.恒温系统在这天保持大棚内温度20℃的时间有10小时
D.恒温系统在这天保持大棚内温度在15 20℃的时间有16小时
6.验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表,根据表中数据,可得y关于x的函数表达式为( )
近视眼镜的度数y(度) 200 250 400 500 1000
镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10
A. B. C. D.
7.小明设计了杠杆平衡实验:如图,取一根长60cm质地均匀的木杆,用细绳绑在木杆的中点O处并将其吊起来,在左侧距离中点O20cm处挂一个重15N的物体,在中点O右侧用一个弹簧测力计竖直向下拉,以保持木杆水平(动力×动力臂=阻力×阻力臂).改变弹簧测力计与中点O的距离L(单位:cm),观察并记录弹簧测力计的示数F(单位:N)有什么变化.小明根据实验得到的下列结论中,不正确的是( )
A.L与F的函数关系式为
B.当L=10时,F=30
C.当L>20时,F>15
D.保持木杆水平,F的最小值为10
8.如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流I(A)与电阻R(Ω)成反比例函数的图象,该图象经过点P(880,0.25).根据图象可知,下列说法不正确的是( )
A.I与R的函数关系式是
B.当I=0.5时,R=440
C.当R>1000时,I>0.22
D.当880<R<1000时,I的取值范围是0.22<I<0.25
9.某气球充满一定质量的气体后,当温度不变时,气球内的气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积至少为( )
A. B. C. D.
10.如图,一块方砖的三个面A,B,C,其中B面为正方形,A,C两个面为矩形,B面的面积小于A面的面积.若将A,B,C三个面分别向下放在桌面上,则地面所受压强分别为PA,PB,PC,压强的计算公式为,其中P是压强,F是压力(由于方砖的重量不变,故F不变),S是受力面积,则PA,PB,PC的大小关系正确的是( )
A.PA>PB>PC B.PA>PC=PB C.PC=PA>PB D.PB>PA=PC
11.某市举行中学生党史知识竞赛,如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率(该校优秀人数与该校参加竞赛人数的比值)y与该校参加竞赛人数x的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是( )
A.甲 B.乙 C.丙 D.丁
12.小亮新买了一盏亮度可调节的台灯(图①),他发现调节的原理是当电压一定时,通过调节电阻控制电流的变化从而改变灯光的明暗,台灯的电流I(A)是电阻R(Ω)的反比例函数,其图象如图②所示.下列说法正确的是( )
A.电流I(A)随电阻R(Ω)的增大而增大
B.电流I(A)与电阻R(Ω)的关系式为
C.当电阻R为550Ω时,电流I为0.5A
D.当电阻R≥1100Ω时,电流I的范围为0<I≤0.2A
二.填空题(共5小题)
13.若梯形的下底长为x,上底长为下底长的,高为y,面积为60,则y与x的函数关系式为 .(不考虑x的取值范围)
14.某蓄电池的电压为48V,使用此蓄电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为.当R=6Ω时,I的值为 A.
15.验光师通过检测发现近视眼镜的度数y(度)与镜片焦距x(米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 度.
16.已知蓄电池的电压为定值.使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则蓄电池的电压是 V.
17.科学发现,若气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(单位:kPa)是关于气体体积V(单位:m3)的反比例函数,如图所示的是恒温下某气球(充满气)的气压与体积的函数图象.当气体体积为2m3时,气压是 kPa.
三.解答题(共5小题)
18.写出函数解析式表示下列关系,并指出它们各是什么函数:
(1)体积是常数V时,圆柱的底面积S与高h的关系;
(2)柳树乡共有耕地面积S(单位:hm2),该乡人均耕地面积y(单位:hm2/人)与全乡总人口x的关系.
19.水塔中储有若干立方米的水,如果每小时放水5m3,那么8小时放完.
(1)求水塔中原有多少立方米的水;
(2)设放水时间为y(h),每小时放水量为x(m3),写出y与x的关系式;
(3)画出(2)中函数的大致图象.
20.某地区上一年度每度电价格为0.8元,年用电量为1亿度,本年度计划将电价调到0.55~0.75元(不包括端点值).经测算,若电价调至x元,则本年度新增用电量y(亿度)与(x﹣0.4)(元)成反比例,且当x=0.65时,y=0.8.
(1)求y与x之间的函数表达式 .
(2)若每度电的成本价为0.3元,当电价调至0.72元时,本年度电力部门的收益是多少元?[收益=用电量×(实际电价﹣成本价)]
21.面积一定的梯形,其上底长是下底长的,设上底长为xcm,高为ycm,且当x=5cm,y=6cm,
(1)求y与x的函数关系式;
(2)求当y=4cm时,下底长多少?
22.一辆汽车准备从甲地开往乙地.若平均速度为80km/h,则需要5h到达.
(1)写出汽车从甲地到乙地所用时间t与平均速度v之间的关系式;
(2)如果准备用8h到达,那么平均速度是多少?
(3)已知汽车的最大平均速度是100km/h,那么汽车最少用多长时间可以到达?
参考答案
一.选择题(共12小题)
1--10CDCAD BCCDD 11--12CD
二.填空题(共5小题)
13.y=
14.8
15.200
16.36
17.100
三.解答题(共5小题)
18.解:(1)由题意可得:S=;
(2)由题意可得:y=.
19.解:(1)5m3×8=40m2,
答:水塔中原有40立方米的水;
(2)∵xy=40,y与x成反比例关系.
∴y与x之间的关系式为y=;
(3)如图所示:
20.解:(1)设y与x之间的函数表达式为 (k≠0).
因为当x=0.65时,y=0.8,所以k=(x﹣0.4)y=(0.65﹣0.4)×0.8=0.2.
所以 即 (0.55<x<0.75).
故答案为: (0.55<x<0.75).
(2)当电价调至0.72元时,本年度新增用电量为 (亿度),则本年度用电量为 1+0.625=1.625(亿度)=1.625×10°(度).
所以( 0.72﹣0.3)×1.625×108=6.825×107 (元).
所以当电价调至0.72元时,本年度电力部门的收益是 6.825×107 元.
21.解:(1)∵x=5cm,y=6cm,上底长是下底长的,
∴下底长为10cm,
∴梯形的面积=(5+10)×6=45,
∵梯形的高=,
∴;
(2)当y=4cm时,x=7.5,
∴2x=15.
答:下底长15cm.
22.解:(1)∵平均速度为80km/h,则需要5h到达,
∴甲地到乙地的距离为80×5=400km,
∴vt=400,
∴汽车从甲地到乙地所用时间t与平均速度v之间的关系式t=;
(2)当t=8时,v==50,
∴平均速度是50km/h;
(3)当v=100时,t==4,
所以汽车最少用4时间可以到达
