第一单元 观察物体(三)(单元检测培优卷) 人教版数学 五年级下册(含解析)
文档属性
| 名称 | 第一单元 观察物体(三)(单元检测培优卷) 人教版数学 五年级下册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 329.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 16:54:26 | ||
图片预览




文档简介
第一单元 观察物体(三)(单元检测培优卷)
人教版数学 五年级下册
一、填空题
1.如图:从( )面看是,从( )面看是,从( )面看是。
2.看图填空。
从( )面看到的形状是,从( )面看到的形状是。
3.用同样的小正方体搭一个立体图形,从上面看到的图形是,从前面看到的图形是,从左面看到的图形是,则这个立体图形是由( )个小正方体组成的。
4.如图的立体图形,要想从上面看形状不变,最多可以拿掉( )个小正方体。
5.用5个小正方体摆成的立体图形,从上面看到的和的上面一样,一共有( )种摆法。
二、判断题
6.一个物体从前面看到的图形是,这个物体一定是由2个小正方体摆成的。( )
7.从左面观察 所看到的图形是。( )
8.一个立体图形从上面看到的图形如图(上面的数字表示在这个位置的小正方体的个数),则这个立体图形从前面看是。( )
9.从正面、左面和上面看到的都是,这个几何体可以摆成。( )
10.拿走图中一个小方块,使从上面和左面看到的图形不变,有2种拿法。( )
三、选择题
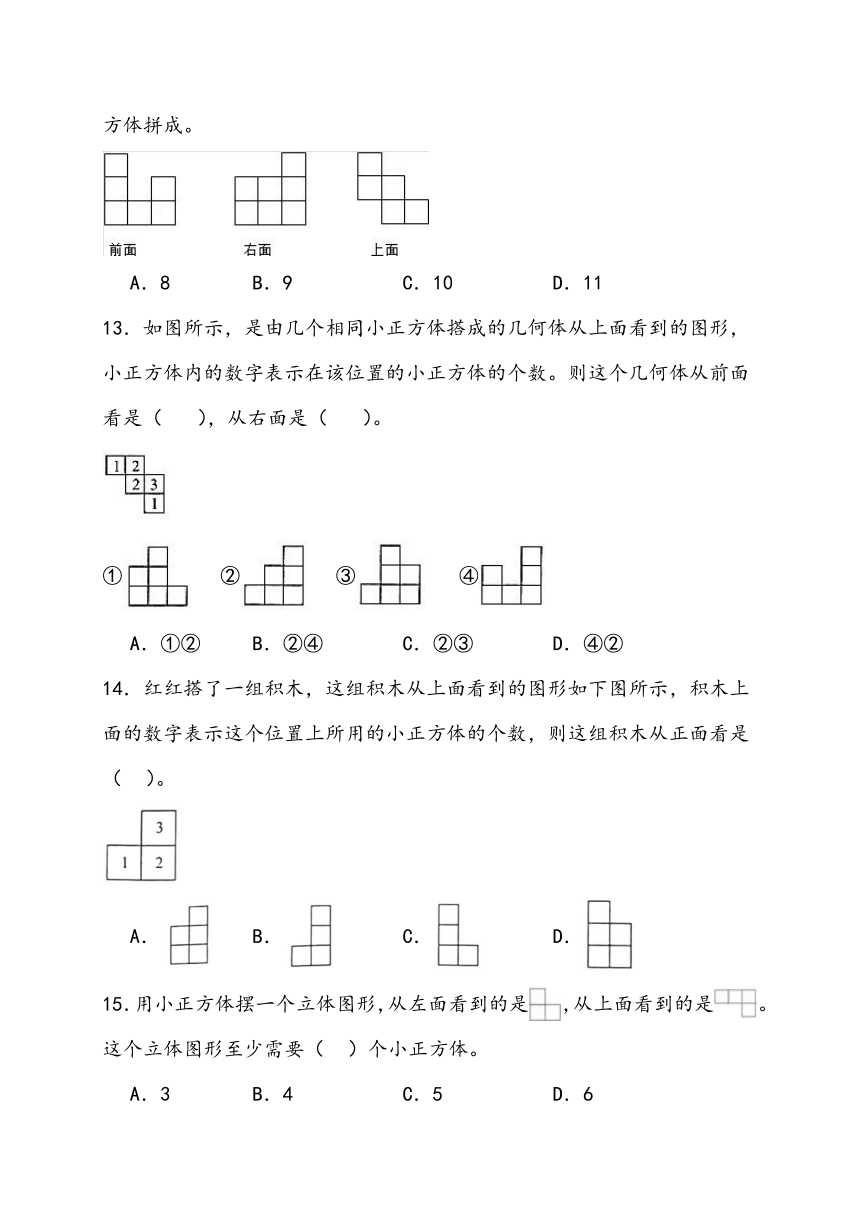
11.一个立体图形,从前面和左面看到的图形均由下图所示,搭成这样的立体图形,最少需要( )个小正方体。
A.4 B.3 C.6 D.5
12.小强观察一个建筑物模型(由若干个相同的小正方体拼成),分别从前面,右面,上面观察,看到的图案如图所示,那么该模型共由( )个小正方体拼成。
A.8 B.9 C.10 D.11
13.如图所示,是由几个相同小正方体搭成的几何体从上面看到的图形,小正方体内的数字表示在该位置的小正方体的个数。则这个几何体从前面看是( ),从右面是( )。
① ② ③ ④
A.①② B.②④ C.②③ D.④②
14.红红搭了一组积木,这组积木从上面看到的图形如下图所示,积木上面的数字表示这个位置上所用的小正方体的个数,则这组积木从正面看是( )。
A. B. C. D.
15.用小正方体摆一个立体图形,从左面看到的是,从上面看到的是。这个立体图形至少需要( )个小正方体。
A.3 B.4 C.5 D.6
四、作图题
16.如图是从上面看到所搭几何体的平面图,方格中数字表示该位置的小正方体个数。请在下图方格中分别画出从正面和左面看到的图形。
五、解答题
17.如图中的网格是边长为1cm的小正方形。
(1)图2是由图1先向右平移( )格,再绕点A按( )时针方向旋转( )°得到的。
(2)在图1中标出点A。
(3)一个由小正方体搭成的几何体,如果从正面和上面看到的都是图1的形状,那么这个几何体的表面积最少是( )cm2。
18.用一些同样的正方体积木在桌面上摆一个几何体,要求从正面、上面和左面看到的图形都是,至少需要用几块正方体积木?最多呢?
19.如下图所示,要使从上面看到的图形不变。
(1)如果有6个小正方体,有几种不同的摆法?可以怎样摆?
(2)如果有7个小正方体,有几种不同的摆法?说说你的理由。
20.把9个棱长是1 cm的小正方体拼在一起(如下图),从正面看和从左面看,所看到的图形的面积之和是多少 取走几号小正方体后,从上面和左面看到的形状不变
参考答案:
1. 侧 正 上
【分析】观察立体图形,从侧面看到的图形有两层,第一层和第二层都有1个小正方形;从正面看到的图形有两行,三列,第一列和第二列都有2个小正方形,第三列有1个小正方形位于第2行;从上面看到的图形有1行,这行有3个小正方形。据此填空即可。
【详解】由分析可知:
从侧面看是,从正面看是,从上面看是。
【点睛】本题考查观察物体,明确从不同方向观察到的形状是解题的关键。
2. 上 左/侧
【分析】根据立体图形从前面、上面、左面看到的形状进行判断即可。
【详解】从上面看:,从前面看:,从左面看:。
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
3.4
【分析】根据题意,从上面看到的图形是,可知底层分左右两列,有2个小正方体,结合从前面看到的图形是,从左面看到的图形是,可知左列有3个小正方体,右列有1个小正方体,据此解答即可。
【详解】3+1=4(个)
则这个立体图形是由4个小正方体组成的。
4.2
【分析】题中图形从上面看到的正方形有两行,共3个小正方形,上面1个,下面2个,右对齐,并且每个小正方形叠加的数量如图:
据此分析解答即可。
【详解】由分析可得:
要使从上面的形状不变,最多可以将做左边叠加3个的正方体,拿走2个。
综上所述:如图的立体图形,要想从上面看形状不变,最多可以拿掉2个小正方体。
【点睛】本题主要考查从不同方向观察物体,需要学生有空间想象能力,可以动手画图协助分析。
5.6
【分析】根据题意, 从上面看到的是,可知用5个小正方体要摆成1列,2层,下面一层为3个,其余2个可以在底层3个上面自由摆放,根据这2个的摆放情况确定摆法;据此解答。
【详解】根据分析,当如图,上面2个叠在一起(阴影部分)前后移动时,有3种摆法;
当如图,上面2个并列(阴影部分)前后移动时,有2种摆法;
当如图,上面2个分开摆放时,有1种摆法;
3+2+1=6(种)
所以,一共有6种摆法。
【点睛】此题考查了观察物体的知识,需要学生发挥空间想象能力。
6.×
【分析】一个物体从前面看到的图形是,只能确定这个物体最少由2个小正方体摆成,每个小正方体后面还可以放无数个这样的小正方体,因此,不能确定它一定是由2个正方体摆成的,据此分析。
【详解】如图,这个物体从前面看到的图形是,这个物体是由6个小正方体摆成的,所以原题说法错误。
故答案为:×
7.×
【分析】观察图形可知,从左面看到的图形有两层,第一层有3个小正方形,第二层有1个小正方形,靠左齐。据此解答即可。
【详解】由分析可知:
从左面观察到的图形是,所以原题干说法错误。
故答案为:×
【点睛】本题考查观察物体,明确从左面看到的形状是解题的关键。
8.×
【分析】观察图形可知,从前面看到的形状有三层,第一层和第二层都有2个正方形,第三层有1个正方形,靠左齐。据此作图即可。
【详解】由分析可知:
这个立体图形从前面看是。原题干说法错误。
故答案为:×
【点睛】本题考查观察物体,明确从前面看到的形状是解题的关键。
9.×
【分析】主视图、左视图、俯视图都是,给想象图形增加了难度,我们可以结合题意在纸上试着一步步画出立体图形,再作判断。
【详解】从正面看是,说明几何体最高是2层,最低是1层;如果结合俯视图也是,基本能够确定,从正面看后排为2个小立方体,前排为1层,2列。每列各有1个小立方体;最后再结合左视图也是,可以最终确定是的形状。即。
故答案为×。
【点睛】由三视图确定几何体,就本题来说,有一定的难度。需要我们充分发挥空间思维,在一次次试验中逐步确定几何体的形状。
10.√
【分析】从上面看到的图形确定每个位置上的小正方体,从上面看到的图形不变,则只能去掉第2层的小正方体;从左面看到的图形可以确定每个位置上小正方体的最高层数,从左面看到的图形左边两列最高层数为2层,从左面看到的图形不变,则只能去掉该立体图形最后边一行的第二层两个小正方体中的一个,据此解答。
【详解】
如图所示,拿走图中一个小方块,使从上面和左面看到的图形不变,有2种拿法。
故答案为:√
【点睛】先确定可以拿走的3个小正方体不改变从上面看到的图形,再从3个小正方体中确定可以拿走的2个小正方体不改变从左面看到的图形。
11.A
【解析】略
12.B
【分析】此题属于简单图形覆盖现象中的规律问题,考查学生的空间想象力。
【详解】3+2+1+1+2=9(个)
故答案为:B
13.C
【分析】做此类题目时,从上面看到同一列最多的小正方体数量即为最后从正面看到的小正方体对应列的数量,即从正面看第一列应只有一个小正方形,第二列有两个,第三列有三个。从右面看有三行,最里面一行有两层,中间一行有三层,最外面一层有一层,据此选择。
【详解】从正面看第一列应只有一个小正方形,第二列有两个,第三列有三个,从右面看有三行,最里面一行有两层,中间一行有三层,最外面一层有一层。
故答案为:C
【点睛】本题考查空间几何观察能力。
14.B
【分析】根据画出红红搭的这组积木,再根据对三视图的认识,即可解答。
【详解】根据可知,红红搭的积木为:;
A.是从右面看到的;
B.是从正面看到的;
C.是从后面看到的;
D.是从左面看到的;
故答案为:B
【点睛】正确画出这组积木的摆放图是解题关键。
15.C
【分析】此题主要考查了观察物体的知识,根据从上面看到的图形可知,这个图形有两行,后面一行3个正方体,前面一行1个正方体居右;根据从左面看到的图形可知,这个图形有两列,左边一列最高为2个正方体,右边一列最高为1个正方体;结合左视图、俯视图,能够确定这个组合体后面一行底层有3个小正方体,上层至少有1个小正方体;前面一行只有一个小正方体,居右;这样算来,最少需要5个小正方体摆出这个立体图形。
【详解】用小正方体摆一个立体图形,从左面看到的是,从上面看到的是。这个立体图形组合方式可以为以下一种:;;;;;;。则至少需要5个小正方体。
故答案为:C。
【点睛】问题是“至少需要几个小正方体”,“至少”二字增加了难度。就是增加了不确定性,需要我们考虑透彻、全面。
16.见详解
【分析】根据从上面看到的几何体的平面图,可以得出:从正面看有3列,共6个小正方体;从左往右,分别是3个、1个、2个;从左面看有3行,从左往右,分别是3个、2个、1个;据此画出从正面看、从左面看的平面图形。
【详解】结合从上面看到的平面图,可以得出下面的几何体:
可以画出从正面和左面看到的图形:
【点睛】具备根据部分视图还原立体图形的能力,从而画出其他视图。
17.(1)6;逆;90
(2)见详解
(3)22
【分析】(1)平移是指在平面内,将一个图形沿着某个方向移动一定的距离,称为平移;旋转是指在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
(2)旋转中心是不动的,据此找到点A的位置。
(3)从正面和上面看到的都是图1的形状,那么这个几何体至少用了5个正方体拼成,如图:,这个几何体的上下面各有4个小正方形,左右面各有3个小正方形,前后面各有4个小正方形;先计算出正方形的总个数,再乘每个正方形的面积,就是几何体最少的表面积。
【详解】(1)先确定旋转中心A点,将图1向右平移6格,图1点A与图2点A重合,再将图1绕点逆时针旋转90°可得到图2;
(2)在图1中标出点A,作图如下:
(3)拼成的几何体是。
(4+3+4)×2
=11×2
=22(个)
1×1×22=22(cm2)
【点睛】掌握图形的平移、旋转的特点,以及能根据部分视图还原立体图形是解题的关键。
18.6块;8块
【分析】根据从上面看到的图形是, 可以知道底层需要4块积木,如图摆放: 。根据从正面看到的图形是 ,可以知道左右两列都有两层;根据从左面看到的图形是 ,可以知道在前后两行也都有两层。综合从正面和左面看到的图形可以知道第二层上至少应摆放2个小正方体,如图摆放: 、 ;最多可摆放4个小正方体,如图摆放:。
【详解】至少需要6块:、。
最多可摆放8个小正方体,如图摆放:。
答:至少需要用6块正方体积木,最多需要用8块正方体积木。
【点睛】本题考查观察物体,解答本题的关键是掌握根据从不同方向看到的图形确定物体形状的方法。
19.(1)有5种不同的摆法(上面的数字表示在这个位置上所用的小正方体的个数)如图:
(2)有15种不同的摆法,理由见解析。
【分析】根据从上面看到的图形的特点,可知这个几何体有两排,第一排有4个小正方体,第二排的最右边有一个小正方体;这时有5个正方体为;
(1)如果有6个小正方体,则是在再加上一个小正方体,则这个小正方体应该放在第二层中,所以有5个不同的拼法;
(2)如果有7个小正方体,则是要在上再加上2个小正方体,1个正方体上摆2个正方体的情况有5种;2个正方体上各摆1个正方体的情况有4+3+2+1=10(种),所以一共有10+5 =15(种);据此解答。
【详解】(1)如果有6个小正方体,有5种不同的摆法(上面的数字表示在这个位置上所用的小正方体的个数)
(2)如果有7个小正方体,有15种不同的摆法。理由:1个正方体上摆2个正方体的情况有5种;2个正方体上各摆1个正方体的情况有4+3+2+1=10(种),所以一共有10+5=15(种)。
【点睛】本题考查了从不同的角度观察物体,关键是要掌握从不同角度观察到几何体的图形的特点,学会从观察到的图形分析几何体的形状。
20.11cm2 3号
【详解】1×1×(6+5)=11(cm2)
取走3号小正方体后,从上面和左面看到的形状不变。
人教版数学 五年级下册
一、填空题
1.如图:从( )面看是,从( )面看是,从( )面看是。
2.看图填空。
从( )面看到的形状是,从( )面看到的形状是。
3.用同样的小正方体搭一个立体图形,从上面看到的图形是,从前面看到的图形是,从左面看到的图形是,则这个立体图形是由( )个小正方体组成的。
4.如图的立体图形,要想从上面看形状不变,最多可以拿掉( )个小正方体。
5.用5个小正方体摆成的立体图形,从上面看到的和的上面一样,一共有( )种摆法。
二、判断题
6.一个物体从前面看到的图形是,这个物体一定是由2个小正方体摆成的。( )
7.从左面观察 所看到的图形是。( )
8.一个立体图形从上面看到的图形如图(上面的数字表示在这个位置的小正方体的个数),则这个立体图形从前面看是。( )
9.从正面、左面和上面看到的都是,这个几何体可以摆成。( )
10.拿走图中一个小方块,使从上面和左面看到的图形不变,有2种拿法。( )
三、选择题
11.一个立体图形,从前面和左面看到的图形均由下图所示,搭成这样的立体图形,最少需要( )个小正方体。
A.4 B.3 C.6 D.5
12.小强观察一个建筑物模型(由若干个相同的小正方体拼成),分别从前面,右面,上面观察,看到的图案如图所示,那么该模型共由( )个小正方体拼成。
A.8 B.9 C.10 D.11
13.如图所示,是由几个相同小正方体搭成的几何体从上面看到的图形,小正方体内的数字表示在该位置的小正方体的个数。则这个几何体从前面看是( ),从右面是( )。
① ② ③ ④
A.①② B.②④ C.②③ D.④②
14.红红搭了一组积木,这组积木从上面看到的图形如下图所示,积木上面的数字表示这个位置上所用的小正方体的个数,则这组积木从正面看是( )。
A. B. C. D.
15.用小正方体摆一个立体图形,从左面看到的是,从上面看到的是。这个立体图形至少需要( )个小正方体。
A.3 B.4 C.5 D.6
四、作图题
16.如图是从上面看到所搭几何体的平面图,方格中数字表示该位置的小正方体个数。请在下图方格中分别画出从正面和左面看到的图形。
五、解答题
17.如图中的网格是边长为1cm的小正方形。
(1)图2是由图1先向右平移( )格,再绕点A按( )时针方向旋转( )°得到的。
(2)在图1中标出点A。
(3)一个由小正方体搭成的几何体,如果从正面和上面看到的都是图1的形状,那么这个几何体的表面积最少是( )cm2。
18.用一些同样的正方体积木在桌面上摆一个几何体,要求从正面、上面和左面看到的图形都是,至少需要用几块正方体积木?最多呢?
19.如下图所示,要使从上面看到的图形不变。
(1)如果有6个小正方体,有几种不同的摆法?可以怎样摆?
(2)如果有7个小正方体,有几种不同的摆法?说说你的理由。
20.把9个棱长是1 cm的小正方体拼在一起(如下图),从正面看和从左面看,所看到的图形的面积之和是多少 取走几号小正方体后,从上面和左面看到的形状不变
参考答案:
1. 侧 正 上
【分析】观察立体图形,从侧面看到的图形有两层,第一层和第二层都有1个小正方形;从正面看到的图形有两行,三列,第一列和第二列都有2个小正方形,第三列有1个小正方形位于第2行;从上面看到的图形有1行,这行有3个小正方形。据此填空即可。
【详解】由分析可知:
从侧面看是,从正面看是,从上面看是。
【点睛】本题考查观察物体,明确从不同方向观察到的形状是解题的关键。
2. 上 左/侧
【分析】根据立体图形从前面、上面、左面看到的形状进行判断即可。
【详解】从上面看:,从前面看:,从左面看:。
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力。
3.4
【分析】根据题意,从上面看到的图形是,可知底层分左右两列,有2个小正方体,结合从前面看到的图形是,从左面看到的图形是,可知左列有3个小正方体,右列有1个小正方体,据此解答即可。
【详解】3+1=4(个)
则这个立体图形是由4个小正方体组成的。
4.2
【分析】题中图形从上面看到的正方形有两行,共3个小正方形,上面1个,下面2个,右对齐,并且每个小正方形叠加的数量如图:
据此分析解答即可。
【详解】由分析可得:
要使从上面的形状不变,最多可以将做左边叠加3个的正方体,拿走2个。
综上所述:如图的立体图形,要想从上面看形状不变,最多可以拿掉2个小正方体。
【点睛】本题主要考查从不同方向观察物体,需要学生有空间想象能力,可以动手画图协助分析。
5.6
【分析】根据题意, 从上面看到的是,可知用5个小正方体要摆成1列,2层,下面一层为3个,其余2个可以在底层3个上面自由摆放,根据这2个的摆放情况确定摆法;据此解答。
【详解】根据分析,当如图,上面2个叠在一起(阴影部分)前后移动时,有3种摆法;
当如图,上面2个并列(阴影部分)前后移动时,有2种摆法;
当如图,上面2个分开摆放时,有1种摆法;
3+2+1=6(种)
所以,一共有6种摆法。
【点睛】此题考查了观察物体的知识,需要学生发挥空间想象能力。
6.×
【分析】一个物体从前面看到的图形是,只能确定这个物体最少由2个小正方体摆成,每个小正方体后面还可以放无数个这样的小正方体,因此,不能确定它一定是由2个正方体摆成的,据此分析。
【详解】如图,这个物体从前面看到的图形是,这个物体是由6个小正方体摆成的,所以原题说法错误。
故答案为:×
7.×
【分析】观察图形可知,从左面看到的图形有两层,第一层有3个小正方形,第二层有1个小正方形,靠左齐。据此解答即可。
【详解】由分析可知:
从左面观察到的图形是,所以原题干说法错误。
故答案为:×
【点睛】本题考查观察物体,明确从左面看到的形状是解题的关键。
8.×
【分析】观察图形可知,从前面看到的形状有三层,第一层和第二层都有2个正方形,第三层有1个正方形,靠左齐。据此作图即可。
【详解】由分析可知:
这个立体图形从前面看是。原题干说法错误。
故答案为:×
【点睛】本题考查观察物体,明确从前面看到的形状是解题的关键。
9.×
【分析】主视图、左视图、俯视图都是,给想象图形增加了难度,我们可以结合题意在纸上试着一步步画出立体图形,再作判断。
【详解】从正面看是,说明几何体最高是2层,最低是1层;如果结合俯视图也是,基本能够确定,从正面看后排为2个小立方体,前排为1层,2列。每列各有1个小立方体;最后再结合左视图也是,可以最终确定是的形状。即。
故答案为×。
【点睛】由三视图确定几何体,就本题来说,有一定的难度。需要我们充分发挥空间思维,在一次次试验中逐步确定几何体的形状。
10.√
【分析】从上面看到的图形确定每个位置上的小正方体,从上面看到的图形不变,则只能去掉第2层的小正方体;从左面看到的图形可以确定每个位置上小正方体的最高层数,从左面看到的图形左边两列最高层数为2层,从左面看到的图形不变,则只能去掉该立体图形最后边一行的第二层两个小正方体中的一个,据此解答。
【详解】
如图所示,拿走图中一个小方块,使从上面和左面看到的图形不变,有2种拿法。
故答案为:√
【点睛】先确定可以拿走的3个小正方体不改变从上面看到的图形,再从3个小正方体中确定可以拿走的2个小正方体不改变从左面看到的图形。
11.A
【解析】略
12.B
【分析】此题属于简单图形覆盖现象中的规律问题,考查学生的空间想象力。
【详解】3+2+1+1+2=9(个)
故答案为:B
13.C
【分析】做此类题目时,从上面看到同一列最多的小正方体数量即为最后从正面看到的小正方体对应列的数量,即从正面看第一列应只有一个小正方形,第二列有两个,第三列有三个。从右面看有三行,最里面一行有两层,中间一行有三层,最外面一层有一层,据此选择。
【详解】从正面看第一列应只有一个小正方形,第二列有两个,第三列有三个,从右面看有三行,最里面一行有两层,中间一行有三层,最外面一层有一层。
故答案为:C
【点睛】本题考查空间几何观察能力。
14.B
【分析】根据画出红红搭的这组积木,再根据对三视图的认识,即可解答。
【详解】根据可知,红红搭的积木为:;
A.是从右面看到的;
B.是从正面看到的;
C.是从后面看到的;
D.是从左面看到的;
故答案为:B
【点睛】正确画出这组积木的摆放图是解题关键。
15.C
【分析】此题主要考查了观察物体的知识,根据从上面看到的图形可知,这个图形有两行,后面一行3个正方体,前面一行1个正方体居右;根据从左面看到的图形可知,这个图形有两列,左边一列最高为2个正方体,右边一列最高为1个正方体;结合左视图、俯视图,能够确定这个组合体后面一行底层有3个小正方体,上层至少有1个小正方体;前面一行只有一个小正方体,居右;这样算来,最少需要5个小正方体摆出这个立体图形。
【详解】用小正方体摆一个立体图形,从左面看到的是,从上面看到的是。这个立体图形组合方式可以为以下一种:;;;;;;。则至少需要5个小正方体。
故答案为:C。
【点睛】问题是“至少需要几个小正方体”,“至少”二字增加了难度。就是增加了不确定性,需要我们考虑透彻、全面。
16.见详解
【分析】根据从上面看到的几何体的平面图,可以得出:从正面看有3列,共6个小正方体;从左往右,分别是3个、1个、2个;从左面看有3行,从左往右,分别是3个、2个、1个;据此画出从正面看、从左面看的平面图形。
【详解】结合从上面看到的平面图,可以得出下面的几何体:
可以画出从正面和左面看到的图形:
【点睛】具备根据部分视图还原立体图形的能力,从而画出其他视图。
17.(1)6;逆;90
(2)见详解
(3)22
【分析】(1)平移是指在平面内,将一个图形沿着某个方向移动一定的距离,称为平移;旋转是指在平面内,将一个图形绕一点按某个方向转动一个角度,这样的运动叫做图形的旋转。
(2)旋转中心是不动的,据此找到点A的位置。
(3)从正面和上面看到的都是图1的形状,那么这个几何体至少用了5个正方体拼成,如图:,这个几何体的上下面各有4个小正方形,左右面各有3个小正方形,前后面各有4个小正方形;先计算出正方形的总个数,再乘每个正方形的面积,就是几何体最少的表面积。
【详解】(1)先确定旋转中心A点,将图1向右平移6格,图1点A与图2点A重合,再将图1绕点逆时针旋转90°可得到图2;
(2)在图1中标出点A,作图如下:
(3)拼成的几何体是。
(4+3+4)×2
=11×2
=22(个)
1×1×22=22(cm2)
【点睛】掌握图形的平移、旋转的特点,以及能根据部分视图还原立体图形是解题的关键。
18.6块;8块
【分析】根据从上面看到的图形是, 可以知道底层需要4块积木,如图摆放: 。根据从正面看到的图形是 ,可以知道左右两列都有两层;根据从左面看到的图形是 ,可以知道在前后两行也都有两层。综合从正面和左面看到的图形可以知道第二层上至少应摆放2个小正方体,如图摆放: 、 ;最多可摆放4个小正方体,如图摆放:。
【详解】至少需要6块:、。
最多可摆放8个小正方体,如图摆放:。
答:至少需要用6块正方体积木,最多需要用8块正方体积木。
【点睛】本题考查观察物体,解答本题的关键是掌握根据从不同方向看到的图形确定物体形状的方法。
19.(1)有5种不同的摆法(上面的数字表示在这个位置上所用的小正方体的个数)如图:
(2)有15种不同的摆法,理由见解析。
【分析】根据从上面看到的图形的特点,可知这个几何体有两排,第一排有4个小正方体,第二排的最右边有一个小正方体;这时有5个正方体为;
(1)如果有6个小正方体,则是在再加上一个小正方体,则这个小正方体应该放在第二层中,所以有5个不同的拼法;
(2)如果有7个小正方体,则是要在上再加上2个小正方体,1个正方体上摆2个正方体的情况有5种;2个正方体上各摆1个正方体的情况有4+3+2+1=10(种),所以一共有10+5 =15(种);据此解答。
【详解】(1)如果有6个小正方体,有5种不同的摆法(上面的数字表示在这个位置上所用的小正方体的个数)
(2)如果有7个小正方体,有15种不同的摆法。理由:1个正方体上摆2个正方体的情况有5种;2个正方体上各摆1个正方体的情况有4+3+2+1=10(种),所以一共有10+5=15(种)。
【点睛】本题考查了从不同的角度观察物体,关键是要掌握从不同角度观察到几何体的图形的特点,学会从观察到的图形分析几何体的形状。
20.11cm2 3号
【详解】1×1×(6+5)=11(cm2)
取走3号小正方体后,从上面和左面看到的形状不变。
