高一物理必修二 第六章 圆周运动 单元提高训练(含答案)
文档属性
| 名称 | 高一物理必修二 第六章 圆周运动 单元提高训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 553.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-31 15:31:12 | ||
图片预览


文档简介
高一物理必修二第六章《圆周运动》单元提高训练
一、选择题:
1、2023年5月28日,我国自主研制的大型客运飞机C919从上海虹桥飞抵北京首都国际机场,标志着中国造大飞机正式迈入商业运营阶段。若客机空中转弯时,在t时间内以恒定的速率沿圆弧路径飞行的路程为L,客机相对圆弧圆心转过的角度为,客机的质量为m,下列对客机转弯过程的分析,正确的是( )
A. 转弯半径为L B. 转弯半径为
C. 客机所受向心力大小为 D. 客机所受向心力大小为
2、如图所示为教室里悬挂的走时准确的时钟,时针、分针和秒针可视为做匀速转动,已知分针的长度是时针长度的倍,关于时钟的时针、分针和秒针转动情况的分析,下列说法正确的是( )
A. 时针、分针、秒针三者转动的角速度相等
B. 分针端点的线速度是时针端点的线速度的倍
C. 分针端点的向心加速度是时针端点的向心加速度的倍
D. 分针与时针相邻两次重合间隔的时间为小时
3、如图所示,两个质量均为0.1 kg的小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为0.5 m,b与转轴OO′的距离为1.5 m。木块与圆盘的最大静摩擦力为木块所受重力的0.8倍,取重力加速度g=10 m/s2,圆盘绕转轴以2 rad/s的角速度匀速转动。下列说法正确的是( )
A.a受到的摩擦力大小为0.1 N B.b正在远离转轴
C.改变圆盘绕转轴转动的角速度,b可能向转轴靠近
D.若要使a相对圆盘运动,则圆盘绕转轴转动的角速度应大于4 rad/s
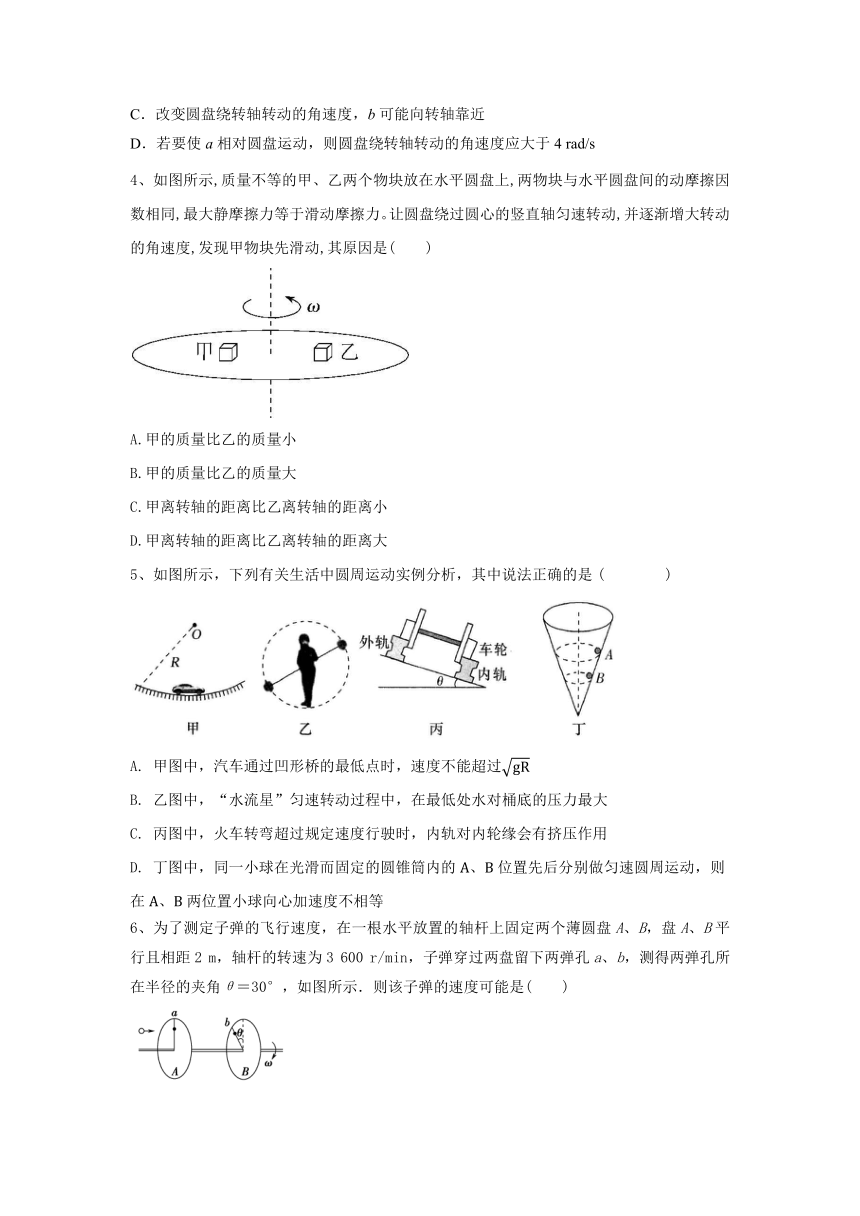
4、如图所示,质量不等的甲、乙两个物块放在水平圆盘上,两物块与水平圆盘间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力。让圆盘绕过圆心的竖直轴匀速转动,并逐渐增大转动的角速度,发现甲物块先滑动,其原因是( )
A.甲的质量比乙的质量小
B.甲的质量比乙的质量大
C.甲离转轴的距离比乙离转轴的距离小
D.甲离转轴的距离比乙离转轴的距离大
5、如图所示,下列有关生活中圆周运动实例分析,其中说法正确的是( )
A. 甲图中,汽车通过凹形桥的最低点时,速度不能超过
B. 乙图中,“水流星”匀速转动过程中,在最低处水对桶底的压力最大
C. 丙图中,火车转弯超过规定速度行驶时,内轨对内轮缘会有挤压作用
D. 丁图中,同一小球在光滑而固定的圆锥筒内的、位置先后分别做匀速圆周运动,则在、两位置小球向心加速度不相等
6、为了测定子弹的飞行速度,在一根水平放置的轴杆上固定两个薄圆盘A、B,盘A、B平行且相距2 m,轴杆的转速为3 600 r/min,子弹穿过两盘留下两弹孔a、b,测得两弹孔所在半径的夹角θ=30°,如图所示.则该子弹的速度可能是( )
A.360 m/s B.720 m/s
C.1 440 m/s D.108 m/s
7、如图所示,物块P置于水平转盘上随转盘一起运动,图中c方向沿半径指向圆心,a方向与c方向垂直。当转盘逆时针转动时,下列说法正确的是( )
A.当转盘匀速转动时,P所受摩擦力方向为c
B.当转盘匀速转动时,P不受转盘的摩擦力
C.当转盘加速转动时,P所受摩擦力方向可能为a
D.当转盘减速转动时,P所受摩擦力方向可能为b
8、如图所示,OO'为竖直轴,MN为固定在OO'上的水平光滑杆,有两个质量相同的金属球A、B套在水平杆上,AC和BC为抗拉能力相同的两根细线,C端固定在转轴OO'上。当细线拉直时,A、B两球转动半径之比恒为2∶1,当转轴的角速度逐渐增大时( )
A.AC先断 B.BC先断
C.两细线同时断 D.不能确定哪根细线先断
9、如图所示,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动。座舱的质量为m,运动半径为R,角速度大小为ω,重力加速度为g,则关于座舱说法不正确的是( )
A.运动周期为 B.线速度的大小为2ωR
C.受摩天轮作用力的大小始终为mg D.所受合力的大小始终为mω2R
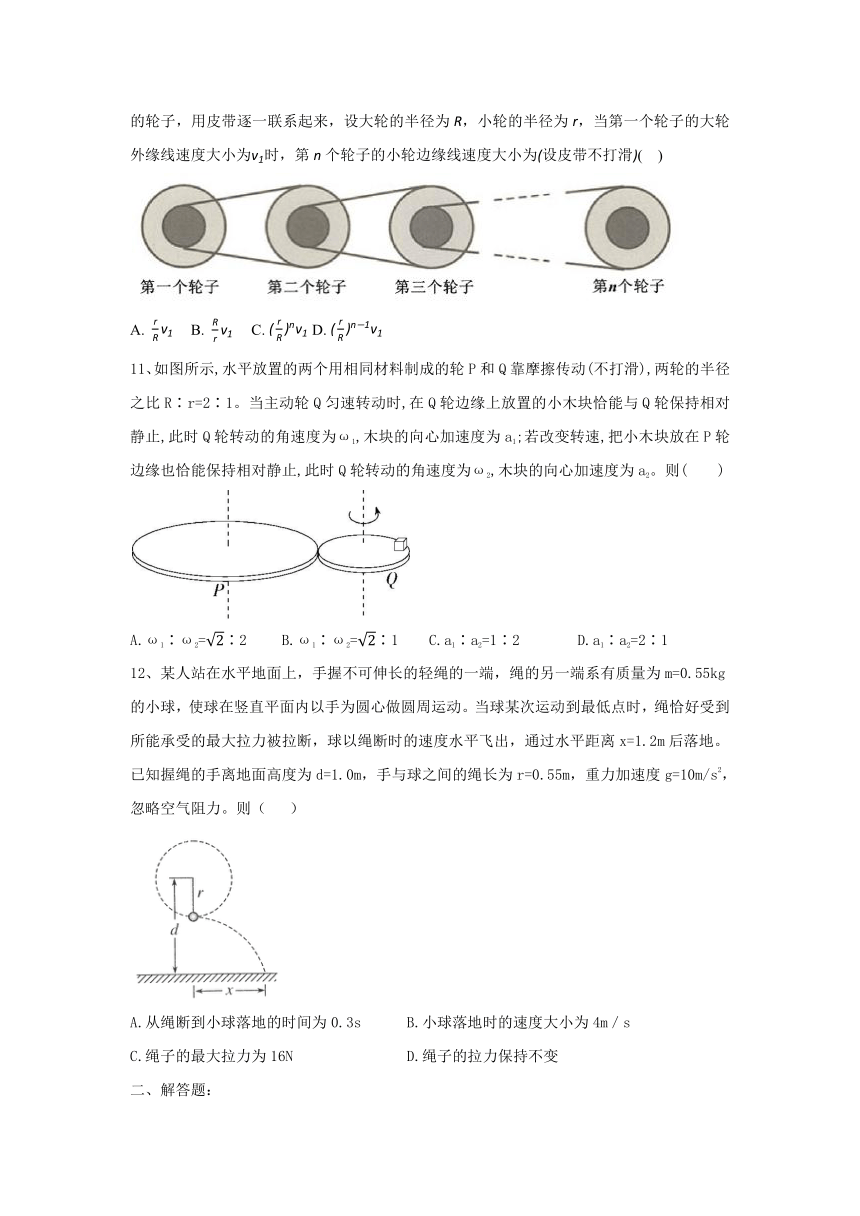
10、如图是多级减速装置的示意图。每一个轮子都由大小两个轮子叠合而成,共有个这样的轮子,用皮带逐一联系起来,设大轮的半径为,小轮的半径为,当第一个轮子的大轮外缘线速度大小为时,第个轮子的小轮边缘线速度大小为设皮带不打滑( )
A. B. C. D.
11、如图所示,水平放置的两个用相同材料制成的轮P和Q靠摩擦传动(不打滑),两轮的半径之比R∶r=2∶1。当主动轮Q匀速转动时,在Q轮边缘上放置的小木块恰能与Q轮保持相对静止,此时Q轮转动的角速度为ω1,木块的向心加速度为a1;若改变转速,把小木块放在P轮边缘也恰能保持相对静止,此时Q轮转动的角速度为ω2,木块的向心加速度为a2。则( )
A.ω1∶ω2=∶2 B.ω1∶ω2=∶1 C.a1∶a2=1∶2 D.a1∶a2=2∶1
12、某人站在水平地面上,手握不可伸长的轻绳的一端,绳的另一端系有质量为m=0.55kg的小球,使球在竖直平面内以手为圆心做圆周运动。当球某次运动到最低点时,绳恰好受到所能承受的最大拉力被拉断,球以绳断时的速度水平飞出,通过水平距离x=1.2m后落地。已知握绳的手离地面高度为d=1.0m,手与球之间的绳长为r=0.55m,重力加速度g=10m/s2,忽略空气阻力。则( )
A.从绳断到小球落地的时间为0.3s B.小球落地时的速度大小为4m/s
C.绳子的最大拉力为16N D.绳子的拉力保持不变
二、解答题:
13、某同学利用图甲所示的DIS向心力实验器来探究砝码做圆周运动所需要向心力F与其质量m、转动半径r和转动线速度v之间的关系。实验时,砝码和挡光杆随旋臂一起做圆周运动,砝码所需的向心力可通过牵引杆由力传感器测得,挡光杆每经过光电门一次,通过力传感器和光电门就同时获得一组向心力F和挡光杆挡光时间t的数据。牵引杆的质量和一切摩擦可忽略。
(1)利用本仪器探究向心力大小的表达式过程中,用到的最主要的科学方法是___________。(选填“理想法”“等效法”“控制变量法”)
(2)为了探究向心力大小与线速度的关系,则应保持_______和_______不变。(用题中给出物理量的符号表示)
(3)已知挡光杆和砝码到转轴的距离均为L,挡光杆的挡光宽度为d,在满足(1)的条件下,改变其转速得到多组F、t的数据,得到F-()2图线如图乙所示。根据图乙得到的实验结论是_______。
(4)求得图线的斜率为k,则砝码的质量为_______。(用题中给出物理量的符号表示)
14、为确保弯道行车安全,汽车进入弯道前必须减速。如图所示,AB为进入弯道前的平直公路,BC为水平圆弧形弯道。已知AB段的距离sAB=14 m,弯道半径R=24 m。汽车到达A点时速度vA=16 m/s,汽车与路面间的动摩擦因数μ=0.6,设最大静摩擦力等于滑动摩擦力,g取10 m/s2。要确保汽车进入弯道后不侧滑。求汽车:
(1)在弯道上行驶的最大速度;
(2)在AB段做匀减速运动的最小加速度;
(3)为提高BC处转弯的最大速度,请提出公路建设时的合理建议(至少写两点)。
15、.如图所示,长为L的细绳,一端拴一质量为m的小球,另一端固定于O点,让其在水平面内做匀速圆周运动(圆锥摆),摆线与竖直方向的夹角为α。求:
(1)细绳的拉力大小F;
(2)小球运动的线速度的大小和向心加速度大小;
(3)小球运动的角速度及周期。
16、如图所示,一根长为的细线,一端系一质量为的小球可视为质点,另一端固定在一光滑锥体顶端,母线与竖直方向的夹角,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为时,细线的拉力为,取。,结果可用根式表示。
若要小球离开锥面,则小球的角速度至少为多大?
若细线与竖直方向的夹角为,则小球的角速度为多大?
当小球的角速度时,细线上的拉力为多大?
17、如图所示,一个可视为质点的质量为m=2 kg的木块从P点以初速度v0=5 m/s向右运动,木块与水平面间的动摩擦因数μ=0.4,木块运动到M点后水平抛出,恰好沿粗糙圆弧AB的A点的切线方向进入圆弧(不计空气阻力)。已知圆弧的半径R=0.5 m,半径OA与竖直半径OB间的夹角θ=53°,木块到达A点时的速度vA=5 m/s,取sin 53°=0.8,cos 53°=0.6,g=10 m/s2。
(1)求P到M的距离l;
(2)求M、A间的距离s;
(3)若木块到达圆弧底端B点时速度大小vB=5 m/s,求此时木块对轨道的压力。
参考答案
参考答案
一、选择题:
1、 D 2、 D 3、D 4、D 5、B
6、 C 7、 A 8、A 9、D 10、C
11、A 12、A
二、解答题:
13、 [1]控制变量法
[2]根据探究向心力大小与线速度的关系,应保持质量m和转动半径r不变;
[3]线速度大小为则有图线斜率表示质量与半径的比值,且保持不变,由此可知,当质量m、转动半径r不变时,向心力与线速度的平方成正比。
[4]由得
14、(1)在BC弯道,由牛顿第二定律得:μmg=代入数据解得vmax=12 m/s
(2)汽车匀减速至B处,速度减为12 m/s时,加速度最小,
由运动学公式-2aminsAB=v-v 代入数据解得amin=4 m/s2
(3)BC弯道路面建成外高内低,增大路面摩擦因数,使BC弯道的弯道半径变大。
15、 (1)因为小球在水平面内做匀速圆周运动,所以小球受到的合力沿水平方向指向圆心O′。由受力分析图可知小球受到的合力大小为mgtan α,细绳对小球的拉力大小为F=。
(2)由牛顿第二定律得:mgtan α=,由几何关系得r=Lsin α,
所以,小球做匀速圆周运动的线速度的大小为v= 。
小球的向心加速度an==gtan α,
(或用牛顿第二定律求解:an===g tan α)。
(3)小球运动的角速度ω=== ,
小球运动的周期T==2π 。
16、若要小球刚好离开锥面,则小球受到重力和细线拉力作用,小球做匀速圆周运动的轨迹圆在水平面上,根据牛顿第二定律可得:
解得 。
同理,当细线与竖直方向成角时,由牛顿第二定律及向心力公式有:
解得: 。
小球的角速度时,小球受到锥面的支持力作用,
对小球受力分析可知,
联立解得。
17、(1)由木块运动到M点后水平抛出,恰好沿粗糙圆弧AB的A点的切线方向进入圆弧可得,M点的速度为:v=vAcos θ=3 m/s
木块在水平面上滑行时的加速度大小a=μg=4 m/s2
P到M的距离l==2 m。
(2)由题图可知,木块运动至A点时竖直方向的分速度为vy=vAsin θ=4 m/s
设M点与A点的水平距离为x,竖直高度为h,有
vy=gt,v=2gh,x=vt,s= 解得s= m。
(3)设木块到达圆弧底端时,底端对木块的支持力为FN,
根据FN-mg=m可得,FN=120 N
由牛顿第三定律可知,木块对轨道的压力大小FN′=FN=120 N,方向竖直向下。
一、选择题:
1、2023年5月28日,我国自主研制的大型客运飞机C919从上海虹桥飞抵北京首都国际机场,标志着中国造大飞机正式迈入商业运营阶段。若客机空中转弯时,在t时间内以恒定的速率沿圆弧路径飞行的路程为L,客机相对圆弧圆心转过的角度为,客机的质量为m,下列对客机转弯过程的分析,正确的是( )
A. 转弯半径为L B. 转弯半径为
C. 客机所受向心力大小为 D. 客机所受向心力大小为
2、如图所示为教室里悬挂的走时准确的时钟,时针、分针和秒针可视为做匀速转动,已知分针的长度是时针长度的倍,关于时钟的时针、分针和秒针转动情况的分析,下列说法正确的是( )
A. 时针、分针、秒针三者转动的角速度相等
B. 分针端点的线速度是时针端点的线速度的倍
C. 分针端点的向心加速度是时针端点的向心加速度的倍
D. 分针与时针相邻两次重合间隔的时间为小时
3、如图所示,两个质量均为0.1 kg的小木块a和b(均可视为质点)放在水平圆盘上,a与转轴OO′的距离为0.5 m,b与转轴OO′的距离为1.5 m。木块与圆盘的最大静摩擦力为木块所受重力的0.8倍,取重力加速度g=10 m/s2,圆盘绕转轴以2 rad/s的角速度匀速转动。下列说法正确的是( )
A.a受到的摩擦力大小为0.1 N B.b正在远离转轴
C.改变圆盘绕转轴转动的角速度,b可能向转轴靠近
D.若要使a相对圆盘运动,则圆盘绕转轴转动的角速度应大于4 rad/s
4、如图所示,质量不等的甲、乙两个物块放在水平圆盘上,两物块与水平圆盘间的动摩擦因数相同,最大静摩擦力等于滑动摩擦力。让圆盘绕过圆心的竖直轴匀速转动,并逐渐增大转动的角速度,发现甲物块先滑动,其原因是( )
A.甲的质量比乙的质量小
B.甲的质量比乙的质量大
C.甲离转轴的距离比乙离转轴的距离小
D.甲离转轴的距离比乙离转轴的距离大
5、如图所示,下列有关生活中圆周运动实例分析,其中说法正确的是( )
A. 甲图中,汽车通过凹形桥的最低点时,速度不能超过
B. 乙图中,“水流星”匀速转动过程中,在最低处水对桶底的压力最大
C. 丙图中,火车转弯超过规定速度行驶时,内轨对内轮缘会有挤压作用
D. 丁图中,同一小球在光滑而固定的圆锥筒内的、位置先后分别做匀速圆周运动,则在、两位置小球向心加速度不相等
6、为了测定子弹的飞行速度,在一根水平放置的轴杆上固定两个薄圆盘A、B,盘A、B平行且相距2 m,轴杆的转速为3 600 r/min,子弹穿过两盘留下两弹孔a、b,测得两弹孔所在半径的夹角θ=30°,如图所示.则该子弹的速度可能是( )
A.360 m/s B.720 m/s
C.1 440 m/s D.108 m/s
7、如图所示,物块P置于水平转盘上随转盘一起运动,图中c方向沿半径指向圆心,a方向与c方向垂直。当转盘逆时针转动时,下列说法正确的是( )
A.当转盘匀速转动时,P所受摩擦力方向为c
B.当转盘匀速转动时,P不受转盘的摩擦力
C.当转盘加速转动时,P所受摩擦力方向可能为a
D.当转盘减速转动时,P所受摩擦力方向可能为b
8、如图所示,OO'为竖直轴,MN为固定在OO'上的水平光滑杆,有两个质量相同的金属球A、B套在水平杆上,AC和BC为抗拉能力相同的两根细线,C端固定在转轴OO'上。当细线拉直时,A、B两球转动半径之比恒为2∶1,当转轴的角速度逐渐增大时( )
A.AC先断 B.BC先断
C.两细线同时断 D.不能确定哪根细线先断
9、如图所示,摩天轮悬挂的座舱在竖直平面内做匀速圆周运动。座舱的质量为m,运动半径为R,角速度大小为ω,重力加速度为g,则关于座舱说法不正确的是( )
A.运动周期为 B.线速度的大小为2ωR
C.受摩天轮作用力的大小始终为mg D.所受合力的大小始终为mω2R
10、如图是多级减速装置的示意图。每一个轮子都由大小两个轮子叠合而成,共有个这样的轮子,用皮带逐一联系起来,设大轮的半径为,小轮的半径为,当第一个轮子的大轮外缘线速度大小为时,第个轮子的小轮边缘线速度大小为设皮带不打滑( )
A. B. C. D.
11、如图所示,水平放置的两个用相同材料制成的轮P和Q靠摩擦传动(不打滑),两轮的半径之比R∶r=2∶1。当主动轮Q匀速转动时,在Q轮边缘上放置的小木块恰能与Q轮保持相对静止,此时Q轮转动的角速度为ω1,木块的向心加速度为a1;若改变转速,把小木块放在P轮边缘也恰能保持相对静止,此时Q轮转动的角速度为ω2,木块的向心加速度为a2。则( )
A.ω1∶ω2=∶2 B.ω1∶ω2=∶1 C.a1∶a2=1∶2 D.a1∶a2=2∶1
12、某人站在水平地面上,手握不可伸长的轻绳的一端,绳的另一端系有质量为m=0.55kg的小球,使球在竖直平面内以手为圆心做圆周运动。当球某次运动到最低点时,绳恰好受到所能承受的最大拉力被拉断,球以绳断时的速度水平飞出,通过水平距离x=1.2m后落地。已知握绳的手离地面高度为d=1.0m,手与球之间的绳长为r=0.55m,重力加速度g=10m/s2,忽略空气阻力。则( )
A.从绳断到小球落地的时间为0.3s B.小球落地时的速度大小为4m/s
C.绳子的最大拉力为16N D.绳子的拉力保持不变
二、解答题:
13、某同学利用图甲所示的DIS向心力实验器来探究砝码做圆周运动所需要向心力F与其质量m、转动半径r和转动线速度v之间的关系。实验时,砝码和挡光杆随旋臂一起做圆周运动,砝码所需的向心力可通过牵引杆由力传感器测得,挡光杆每经过光电门一次,通过力传感器和光电门就同时获得一组向心力F和挡光杆挡光时间t的数据。牵引杆的质量和一切摩擦可忽略。
(1)利用本仪器探究向心力大小的表达式过程中,用到的最主要的科学方法是___________。(选填“理想法”“等效法”“控制变量法”)
(2)为了探究向心力大小与线速度的关系,则应保持_______和_______不变。(用题中给出物理量的符号表示)
(3)已知挡光杆和砝码到转轴的距离均为L,挡光杆的挡光宽度为d,在满足(1)的条件下,改变其转速得到多组F、t的数据,得到F-()2图线如图乙所示。根据图乙得到的实验结论是_______。
(4)求得图线的斜率为k,则砝码的质量为_______。(用题中给出物理量的符号表示)
14、为确保弯道行车安全,汽车进入弯道前必须减速。如图所示,AB为进入弯道前的平直公路,BC为水平圆弧形弯道。已知AB段的距离sAB=14 m,弯道半径R=24 m。汽车到达A点时速度vA=16 m/s,汽车与路面间的动摩擦因数μ=0.6,设最大静摩擦力等于滑动摩擦力,g取10 m/s2。要确保汽车进入弯道后不侧滑。求汽车:
(1)在弯道上行驶的最大速度;
(2)在AB段做匀减速运动的最小加速度;
(3)为提高BC处转弯的最大速度,请提出公路建设时的合理建议(至少写两点)。
15、.如图所示,长为L的细绳,一端拴一质量为m的小球,另一端固定于O点,让其在水平面内做匀速圆周运动(圆锥摆),摆线与竖直方向的夹角为α。求:
(1)细绳的拉力大小F;
(2)小球运动的线速度的大小和向心加速度大小;
(3)小球运动的角速度及周期。
16、如图所示,一根长为的细线,一端系一质量为的小球可视为质点,另一端固定在一光滑锥体顶端,母线与竖直方向的夹角,当小球在水平面内绕锥体的轴做匀速圆周运动的角速度为时,细线的拉力为,取。,结果可用根式表示。
若要小球离开锥面,则小球的角速度至少为多大?
若细线与竖直方向的夹角为,则小球的角速度为多大?
当小球的角速度时,细线上的拉力为多大?
17、如图所示,一个可视为质点的质量为m=2 kg的木块从P点以初速度v0=5 m/s向右运动,木块与水平面间的动摩擦因数μ=0.4,木块运动到M点后水平抛出,恰好沿粗糙圆弧AB的A点的切线方向进入圆弧(不计空气阻力)。已知圆弧的半径R=0.5 m,半径OA与竖直半径OB间的夹角θ=53°,木块到达A点时的速度vA=5 m/s,取sin 53°=0.8,cos 53°=0.6,g=10 m/s2。
(1)求P到M的距离l;
(2)求M、A间的距离s;
(3)若木块到达圆弧底端B点时速度大小vB=5 m/s,求此时木块对轨道的压力。
参考答案
参考答案
一、选择题:
1、 D 2、 D 3、D 4、D 5、B
6、 C 7、 A 8、A 9、D 10、C
11、A 12、A
二、解答题:
13、 [1]控制变量法
[2]根据探究向心力大小与线速度的关系,应保持质量m和转动半径r不变;
[3]线速度大小为则有图线斜率表示质量与半径的比值,且保持不变,由此可知,当质量m、转动半径r不变时,向心力与线速度的平方成正比。
[4]由得
14、(1)在BC弯道,由牛顿第二定律得:μmg=代入数据解得vmax=12 m/s
(2)汽车匀减速至B处,速度减为12 m/s时,加速度最小,
由运动学公式-2aminsAB=v-v 代入数据解得amin=4 m/s2
(3)BC弯道路面建成外高内低,增大路面摩擦因数,使BC弯道的弯道半径变大。
15、 (1)因为小球在水平面内做匀速圆周运动,所以小球受到的合力沿水平方向指向圆心O′。由受力分析图可知小球受到的合力大小为mgtan α,细绳对小球的拉力大小为F=。
(2)由牛顿第二定律得:mgtan α=,由几何关系得r=Lsin α,
所以,小球做匀速圆周运动的线速度的大小为v= 。
小球的向心加速度an==gtan α,
(或用牛顿第二定律求解:an===g tan α)。
(3)小球运动的角速度ω=== ,
小球运动的周期T==2π 。
16、若要小球刚好离开锥面,则小球受到重力和细线拉力作用,小球做匀速圆周运动的轨迹圆在水平面上,根据牛顿第二定律可得:
解得 。
同理,当细线与竖直方向成角时,由牛顿第二定律及向心力公式有:
解得: 。
小球的角速度时,小球受到锥面的支持力作用,
对小球受力分析可知,
联立解得。
17、(1)由木块运动到M点后水平抛出,恰好沿粗糙圆弧AB的A点的切线方向进入圆弧可得,M点的速度为:v=vAcos θ=3 m/s
木块在水平面上滑行时的加速度大小a=μg=4 m/s2
P到M的距离l==2 m。
(2)由题图可知,木块运动至A点时竖直方向的分速度为vy=vAsin θ=4 m/s
设M点与A点的水平距离为x,竖直高度为h,有
vy=gt,v=2gh,x=vt,s= 解得s= m。
(3)设木块到达圆弧底端时,底端对木块的支持力为FN,
根据FN-mg=m可得,FN=120 N
由牛顿第三定律可知,木块对轨道的压力大小FN′=FN=120 N,方向竖直向下。
