第六章 特殊平行四边形 专题2 关于矩形的探究题、作图题(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 专题2 关于矩形的探究题、作图题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1009.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 17:06:07 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
专题2 关于矩形的探究题、作图题
题型1 关于矩形的作图题
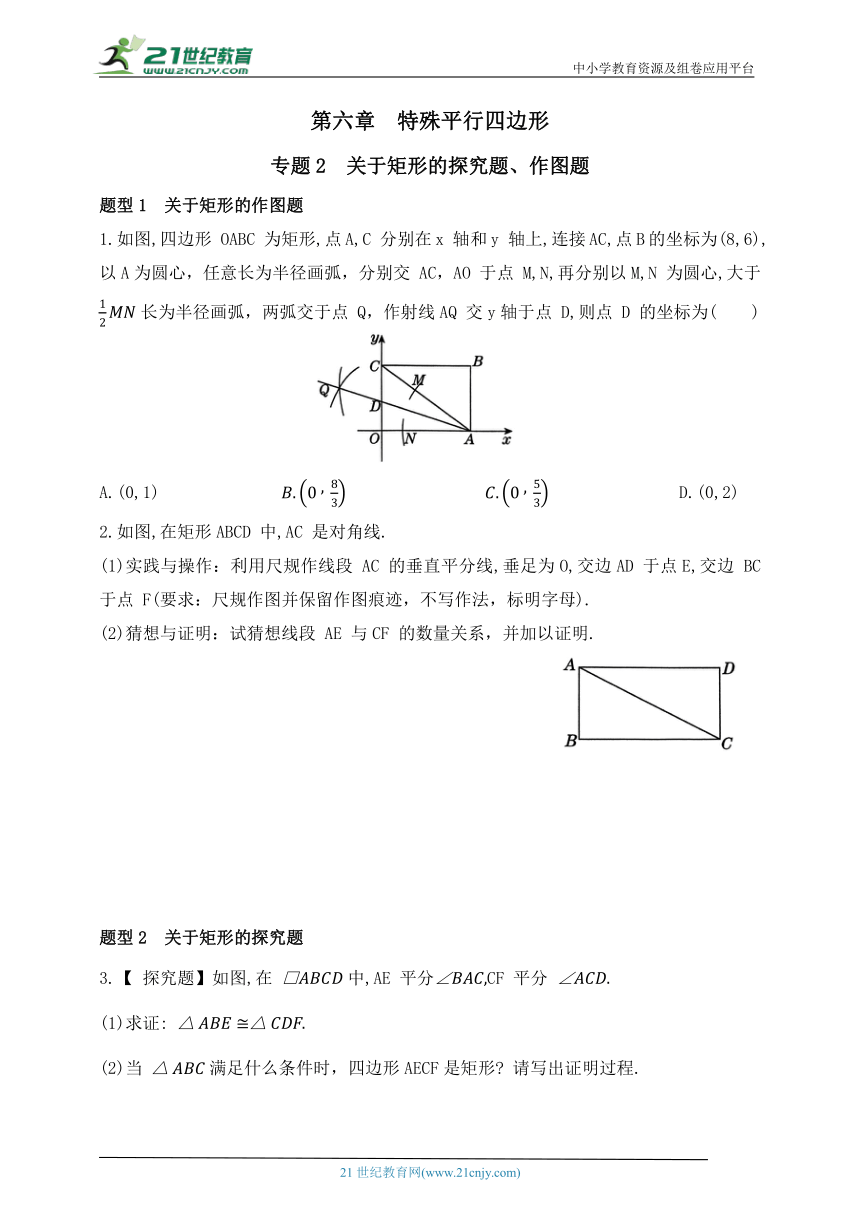
1.如图,四边形 OABC 为矩形,点A,C 分别在x 轴和y 轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交 AC,AO 于点 M,N,再分别以M,N 为圆心,大于 长为半径画弧,两弧交于点 Q,作射线AQ 交y轴于点 D,则点 D 的坐标为( )
A.(0,1) D.(0,2)
2.如图,在矩形ABCD 中,AC 是对角线.
(1)实践与操作:利用尺规作线段 AC 的垂直平分线,垂足为O,交边AD 于点E,交边 BC 于点 F(要求:尺规作图并保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段 AE 与CF 的数量关系,并加以证明.
题型2 关于矩形的探究题
3.【 探究题】如图,在 中,AE 平分CF 平分
(1)求证:
(2)当 满足什么条件时,四边形AECF是矩形 请写出证明过程.
4.如图,在 中,对角线AC 与BD 相交于点 O,点 E,F 分别为OB,OD 的中点,连接AE,CF,延长AE 至点 G,使连接CG.
(1)求证:
(2)当AB 与AC 满足什么数量关系时,四边形EGCF 是矩形 请说明理由.
参考答案
1. B 【点拨】过点 D作 DE⊥AC于点 E,
∵ 四边形OABC 为矩形,点B 的坐标为(8,6),∴ OA =8,
由题意可得 AD平分∠OAC,∴∠DAE=∠DAO.
又∵ ∠AED=90°,∴△ADO≌△ADE(AAS),∴AE=AO=
解得 点
2.【解】 (1)如图.
(2)AE=CF.证明:∵ 四边形 ABCD是矩形,∴AD∥BC,∴ ∠EAO =∠FCO,∠AEO=∠CFO.
∵ EF 是AC 的垂直平分线,∴ AO= CO.
在△AOE 和△COF 中 ∴ △AOE≌△COF(AAS),∴ AE=CF.
3.(1)【证明】∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D,AB∥CD,∴∠BAC=∠ACD.
∵ AE 平分∠BAC,CF 平分∠ACD,∴∠BAE =∴∠BAE=∠DCF.
在△ABE和△CDF中,∴△ABE≌△CDF(ASA).
(2)【解】当△ABC满足AB =AC时,四边形 AECF是矩形.
证明:由(1)易得∠CAE=∠ACF,∴AE∥CF.
∵△ABE≌△CDF,∴AE=CF,∴ 四边形AECF 是平行四边形.
又∵AB=AC,AE平分∠BAC,∴AE⊥BC,∴∠AEC=90°,∴ AECF 是矩形.(答案不唯一)
4.(1)【证明】∵ 四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,∴∠ABE=∠CDF.
∵E,F分别为 OB,OD 的中点,
在△ABE 和 中,
(2)【解】 时,四边形 EGCF是矩形. 理由如下:
「あ 是
OB的中点, 同理:OD, ∥∥
由(1)得
∴四边形EGCF 是平行四边形.
∴四边形EGCF 是矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
专题2 关于矩形的探究题、作图题
题型1 关于矩形的作图题
1.如图,四边形 OABC 为矩形,点A,C 分别在x 轴和y 轴上,连接AC,点B的坐标为(8,6),以A为圆心,任意长为半径画弧,分别交 AC,AO 于点 M,N,再分别以M,N 为圆心,大于 长为半径画弧,两弧交于点 Q,作射线AQ 交y轴于点 D,则点 D 的坐标为( )
A.(0,1) D.(0,2)
2.如图,在矩形ABCD 中,AC 是对角线.
(1)实践与操作:利用尺规作线段 AC 的垂直平分线,垂足为O,交边AD 于点E,交边 BC 于点 F(要求:尺规作图并保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段 AE 与CF 的数量关系,并加以证明.
题型2 关于矩形的探究题
3.【 探究题】如图,在 中,AE 平分CF 平分
(1)求证:
(2)当 满足什么条件时,四边形AECF是矩形 请写出证明过程.
4.如图,在 中,对角线AC 与BD 相交于点 O,点 E,F 分别为OB,OD 的中点,连接AE,CF,延长AE 至点 G,使连接CG.
(1)求证:
(2)当AB 与AC 满足什么数量关系时,四边形EGCF 是矩形 请说明理由.
参考答案
1. B 【点拨】过点 D作 DE⊥AC于点 E,
∵ 四边形OABC 为矩形,点B 的坐标为(8,6),∴ OA =8,
由题意可得 AD平分∠OAC,∴∠DAE=∠DAO.
又∵ ∠AED=90°,∴△ADO≌△ADE(AAS),∴AE=AO=
解得 点
2.【解】 (1)如图.
(2)AE=CF.证明:∵ 四边形 ABCD是矩形,∴AD∥BC,∴ ∠EAO =∠FCO,∠AEO=∠CFO.
∵ EF 是AC 的垂直平分线,∴ AO= CO.
在△AOE 和△COF 中 ∴ △AOE≌△COF(AAS),∴ AE=CF.
3.(1)【证明】∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D,AB∥CD,∴∠BAC=∠ACD.
∵ AE 平分∠BAC,CF 平分∠ACD,∴∠BAE =∴∠BAE=∠DCF.
在△ABE和△CDF中,∴△ABE≌△CDF(ASA).
(2)【解】当△ABC满足AB =AC时,四边形 AECF是矩形.
证明:由(1)易得∠CAE=∠ACF,∴AE∥CF.
∵△ABE≌△CDF,∴AE=CF,∴ 四边形AECF 是平行四边形.
又∵AB=AC,AE平分∠BAC,∴AE⊥BC,∴∠AEC=90°,∴ AECF 是矩形.(答案不唯一)
4.(1)【证明】∵ 四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,∴∠ABE=∠CDF.
∵E,F分别为 OB,OD 的中点,
在△ABE 和 中,
(2)【解】 时,四边形 EGCF是矩形. 理由如下:
「あ 是
OB的中点, 同理:OD, ∥∥
由(1)得
∴四边形EGCF 是平行四边形.
∴四边形EGCF 是矩形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
