第六章 特殊平行四边形 3 正方形的性质与判定 第1课时 正方形的性质(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 3 正方形的性质与判定 第1课时 正方形的性质(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-30 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
3 正方形的性质与判定
第1课时 正方形的性质
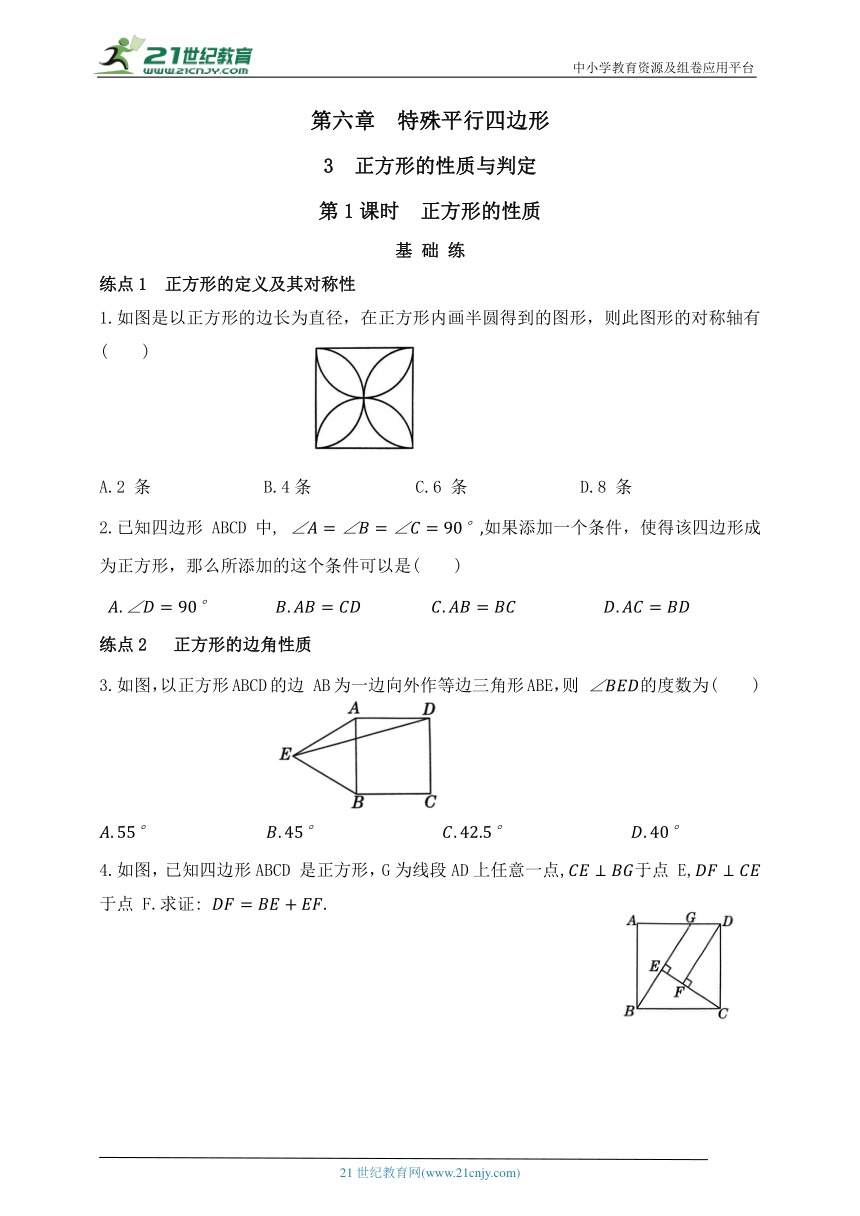
基 础 练
练点1 正方形的定义及其对称性
1.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2 条 B.4条 C.6 条 D.8 条
2.已知四边形 ABCD中, 如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )
练点2 正方形的边角性质
3.如图,以正方形ABCD的边 AB为一边向外作等边三角形ABE,则 的度数为( )
4.如图,已知四边形ABCD 是正方形,G为线段AD上任意一点,于点 E,于点 F.求证:
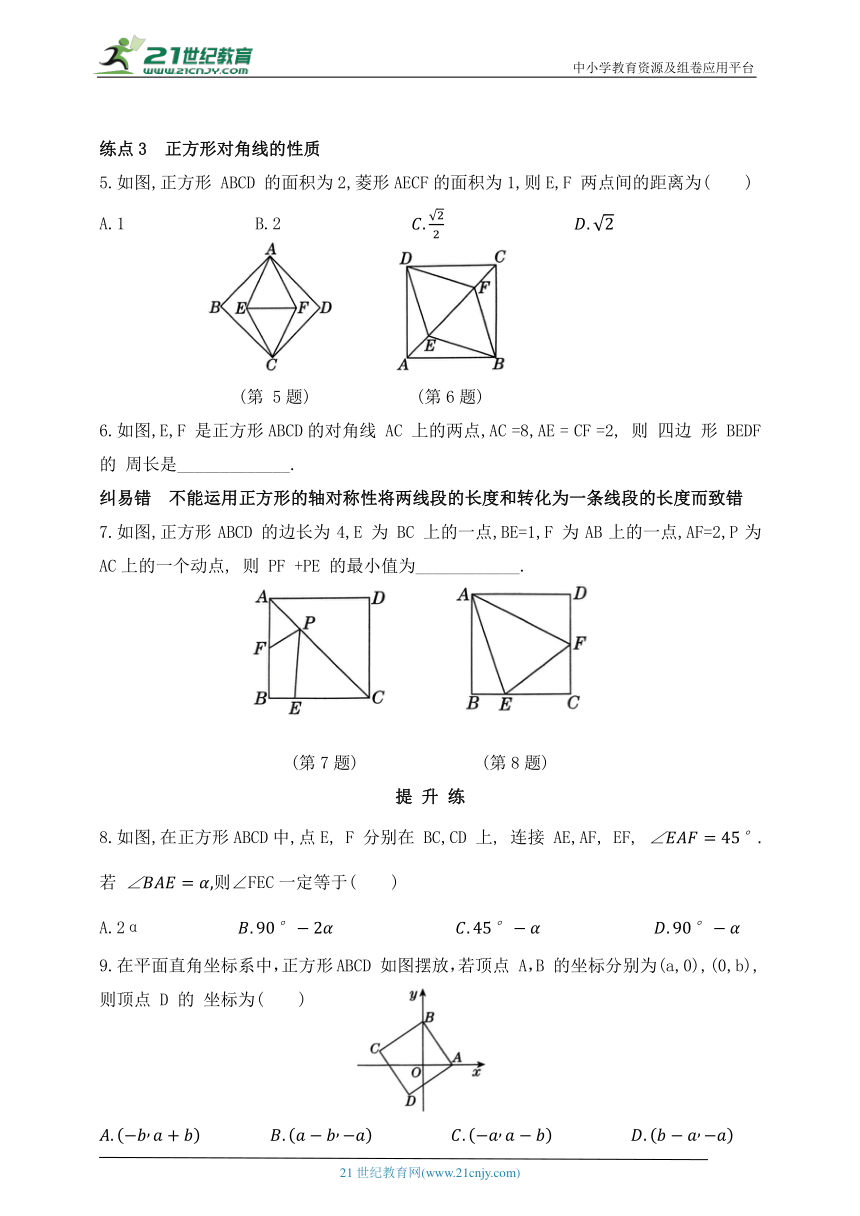
练点3 正方形对角线的性质
5.如图,正方形 ABCD 的面积为2,菱形AECF的面积为1,则E,F 两点间的距离为( )
A.1 B.2
(第 5题) (第6题)
6.如图,E,F 是正方形ABCD的对角线 AC 上的两点,AC =8,AE = CF =2, 则 四边 形 BEDF 的 周长是_____________.
纠易错 不能运用正方形的轴对称性将两线段的长度和转化为一条线段的长度而致错
7.如图,正方形ABCD 的边长为4,E 为 BC 上的一点,BE=1,F 为AB上的一点,AF=2,P为AC上的一个动点, 则 PF +PE 的最小值为____________.
(第7题) (第8题)
提 升 练
8.如图,在正方形ABCD中,点E, F 分别在 BC,CD 上, 连接 AE,AF, EF, 若 则∠FEC一定等于( )
A.2α
9.在平面直角坐标系中,正方形ABCD 如图摆放,若顶点 A,B 的坐标分别为(a,0),(0,b),则顶点 D 的 坐标为( )
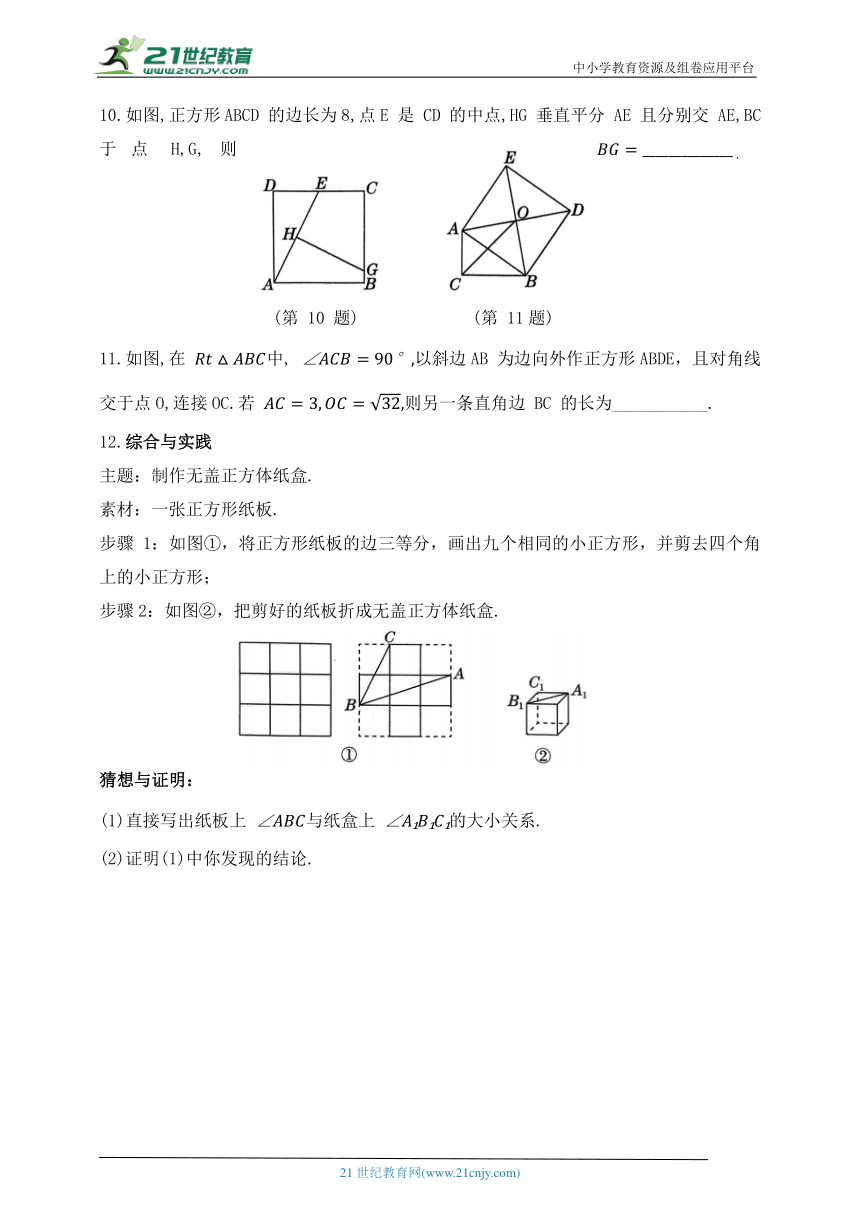
10.如图,正方形ABCD 的边长为8,点E 是 CD 的中点,HG 垂直平分 AE 且分别交 AE,BC
于点H,G,则
(第 10 题) (第 11题)
11.如图,在 中, 以斜边AB 为边向外作正方形ABDE,且对角线交于点O,连接OC.若 则另一条直角边 BC 的长为___________.
12.综合与实践
主题:制作无盖正方体纸盒.
素材:一张正方形纸板.
步骤 1:如图①,将正方形纸板的边三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤2:如图②,把剪好的纸板折成无盖正方体纸盒.
猜想与证明:
(1)直接写出纸板上 与纸盒上 的大小关系.
(2)证明(1)中你发现的结论.
13.如图,已知正方形ABCD,点P在边BC的延长线上,连接AP交BD于F,过点C作∥AP 交 BD 于点 G,连接AG,CF.
(1)求证:
(2)判断四边形 AGCF 是什么特殊四边形 请说明理由.
14.如图,正方形ABCD的对角线AC,BD 相交于点 O,G是CD边上一点,连接BG 交 AC 于点 E,过点 A 作 垂足为M,AM交 BD 于点 F.
(1)求证:
(2)若 BG平分 求证:
参考答案
1. B 2. C
3. B 【点拨】∵ 四边形ABCD 是正方形,∴∠DAB=90°,AD =AB.
∵ △ABE 是等边三角形,∴∠AEB =∠EAB = 60°,AE = AB,∴ ∠DAE = 150°,AE = AD,
(180°-150°) =15°,∴ ∠BED=∠AEB -∠AED=60°-15°=45°.
4.【证明】∵ 四边形 ABCD 是正方形,∴ BC = CD, ∠BCD=90°,∴∠BCE+∠DCF=90°.
∵CE⊥BG,DF⊥CE,∴ ∠BEC = ∠DFC = 90°,∴∠BCE +∠CBE = 90°,∴ ∠CBE =∠DCF.
在△CBE 和△DCF 中, △DCF(AAS),∴CF = BE,CE = DF.
∵ CE = EF +CF,∴DF=BE +EF.
5. A 【点拨】连接AC,BD,∵正方形ABCD的面积是
∵菱 形AECF 的面积是 1,·EF=1,∴EF=1.
【点拨】连接 BD 交 AC 于点 O.
∵ 四边形ABCD 是正方形,
∵AE=CF=2,∴OA-AE=OC-CF=2,∴OE=OF=2.
又∵OB=OD,EF⊥BD,∴ 四边形BEDF 是菱形, ∴ BE = DE = DF = BF.
在 Rt△ODE 中,DE = ∴ 四边形 BEDF 的周长为
7. 【点拨】在 AD 上取一点 M,使得 AM =2,易知点 F,M关于直线 AC 对称.
连接EM ,交 AC 于点P',连接P'F,易得 即 EM 的长为PF +PE的最小值.
过点M作MN⊥BC 于点N,由题意易知EN=BN - BE=AM- BE=2-1 =1,MN=4,所以
点易错 此类问题容易出错的地方是不能将两条线段的长度和转化为一条线段的长度.
8. A 【点拨】在正方形ABCD中,AD=AB,∠BAD=∠ABC=∠ADC=90°.
将△ADF 绕点 A顺时针旋转90°,得 △ABG,则 AF = AG, ∠DAF = ∠BAG.
∵∠EAF=45°,∴ ∠BAE +∠DAF =45°,∴∠BAE+∠BAG=45°,即∠GAE=45°,
∴∠GAE =∠FAE.
在△GAE 和△FAE 中 △FAE(SAS),∴∠AEF=∠AEG.
∵∠BAE=α,∴∠AEB=90°-α,∴∠AEF =∠AEB =90°-α,
∴∠FEC=180°-∠AEF-∠AEB=180°-2×(90°-α) =2α.
9. B 【点拨】过点 D作DE⊥x轴于点 E,
∵ 四边形ABCD 是 正 方 形, ∴AB= AD, ∠BAD = 90°.
∵∠AOB=90°,∴ ∠BAO +∠DAO = ∠ABO +∠BAO = 90°, ∴ ∠ABO = ∠DAO.
∵ ∠AOB =∠DEA=90°,∴△ABO≌△DAE(AAS),∴DE=OA,AE=OB.
∵点A,B 的坐标分别为(a,0),(0,b), ∴OA=a,OB =b,∴ DE =a,AE =b,∴OE =b-a,
∴顶点 D 的坐标为(a-b,-a).
10.1 【点拨】连接AG,EG,∵ 四边形 ABCD 是正方形,∴∠B=∠C=90°.
∵E 是 CD的中点,∴DE=CE=4,设 CG=x,则 BG=8-x.
∵ HG 垂直平分AE,∴ AG = EG. ∴ 根据勾股定理,得
即 解得 x =7,
∴BG=BC-CG=8-7=1.
11.5 【点拨】如图,过点 O 作OF⊥BC于点F,过点A 作AM⊥OF 于点M,
则∠OFC=∠OFB=∠AMF=∠AMO=90°.
又∵∠ACB =90°,∴ 四边形 F BACFM 是矩形,∴AM=CF,MF =AC=3.
∵四边形ABDE 为正方形,
又∵
是等腰直角三角形,
∵FM =4-3=1,∴BC=CF+BF=4+1=5.
12.(1)【解】
(2)【证明】由正方形的性质可知
连接 AC,设每个小正方形的边长为1,则
∴∴△ABC是等腰直角三角形,且∠ACB = 90°,∴∠ABC=45°,
∴∠ABC=∠A B C .
13.(1)【证明】∵ 四边形ABCD 是正方形,∴ AD=BC,∠DBC=∠ADB=45°.
∵CG∥AP,∴∠BGC=∠BFP.∵∠BFP=∠AFD,∴∠AFD=∠BGC.
在△ADF和△CBG中 ∴△ADF≌△CBG(AAS).
(2)【解】四边形 AGCF 是菱形. 理由如下:
连接AC,交 BD 于点 O.
∵ 四边形 ABCD 是正方形, ∴OA=OC,OB =OD,AC⊥BD.
由(1)知△ADF≌△CBG,∴DF=BG,∴OB-BG=OD-FD,∴OG=OF.
又∵OA=OC,∴四边形AGCF 为平行四边形.
∵AC⊥FG,∴四边形AGCF 是菱形.
14.【证明】(1)∵ 四边形ABCD 是正方形;
.
在△AOF和△BOE中,
(2)如图,在 BG上取一点 H,使连接OH,
∵ O 为BD的中点,∴ OH是的中位线,∥
∵四边形ABCD 是正方形,45°,
∴ ∠FOH = 45°.∴∠OCB =∠FOH.
∵ BG 平分
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
3 正方形的性质与判定
第1课时 正方形的性质
基 础 练
练点1 正方形的定义及其对称性
1.如图是以正方形的边长为直径,在正方形内画半圆得到的图形,则此图形的对称轴有( )
A.2 条 B.4条 C.6 条 D.8 条
2.已知四边形 ABCD中, 如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )
练点2 正方形的边角性质
3.如图,以正方形ABCD的边 AB为一边向外作等边三角形ABE,则 的度数为( )
4.如图,已知四边形ABCD 是正方形,G为线段AD上任意一点,于点 E,于点 F.求证:
练点3 正方形对角线的性质
5.如图,正方形 ABCD 的面积为2,菱形AECF的面积为1,则E,F 两点间的距离为( )
A.1 B.2
(第 5题) (第6题)
6.如图,E,F 是正方形ABCD的对角线 AC 上的两点,AC =8,AE = CF =2, 则 四边 形 BEDF 的 周长是_____________.
纠易错 不能运用正方形的轴对称性将两线段的长度和转化为一条线段的长度而致错
7.如图,正方形ABCD 的边长为4,E 为 BC 上的一点,BE=1,F 为AB上的一点,AF=2,P为AC上的一个动点, 则 PF +PE 的最小值为____________.
(第7题) (第8题)
提 升 练
8.如图,在正方形ABCD中,点E, F 分别在 BC,CD 上, 连接 AE,AF, EF, 若 则∠FEC一定等于( )
A.2α
9.在平面直角坐标系中,正方形ABCD 如图摆放,若顶点 A,B 的坐标分别为(a,0),(0,b),则顶点 D 的 坐标为( )
10.如图,正方形ABCD 的边长为8,点E 是 CD 的中点,HG 垂直平分 AE 且分别交 AE,BC
于点H,G,则
(第 10 题) (第 11题)
11.如图,在 中, 以斜边AB 为边向外作正方形ABDE,且对角线交于点O,连接OC.若 则另一条直角边 BC 的长为___________.
12.综合与实践
主题:制作无盖正方体纸盒.
素材:一张正方形纸板.
步骤 1:如图①,将正方形纸板的边三等分,画出九个相同的小正方形,并剪去四个角上的小正方形;
步骤2:如图②,把剪好的纸板折成无盖正方体纸盒.
猜想与证明:
(1)直接写出纸板上 与纸盒上 的大小关系.
(2)证明(1)中你发现的结论.
13.如图,已知正方形ABCD,点P在边BC的延长线上,连接AP交BD于F,过点C作∥AP 交 BD 于点 G,连接AG,CF.
(1)求证:
(2)判断四边形 AGCF 是什么特殊四边形 请说明理由.
14.如图,正方形ABCD的对角线AC,BD 相交于点 O,G是CD边上一点,连接BG 交 AC 于点 E,过点 A 作 垂足为M,AM交 BD 于点 F.
(1)求证:
(2)若 BG平分 求证:
参考答案
1. B 2. C
3. B 【点拨】∵ 四边形ABCD 是正方形,∴∠DAB=90°,AD =AB.
∵ △ABE 是等边三角形,∴∠AEB =∠EAB = 60°,AE = AB,∴ ∠DAE = 150°,AE = AD,
(180°-150°) =15°,∴ ∠BED=∠AEB -∠AED=60°-15°=45°.
4.【证明】∵ 四边形 ABCD 是正方形,∴ BC = CD, ∠BCD=90°,∴∠BCE+∠DCF=90°.
∵CE⊥BG,DF⊥CE,∴ ∠BEC = ∠DFC = 90°,∴∠BCE +∠CBE = 90°,∴ ∠CBE =∠DCF.
在△CBE 和△DCF 中, △DCF(AAS),∴CF = BE,CE = DF.
∵ CE = EF +CF,∴DF=BE +EF.
5. A 【点拨】连接AC,BD,∵正方形ABCD的面积是
∵菱 形AECF 的面积是 1,·EF=1,∴EF=1.
【点拨】连接 BD 交 AC 于点 O.
∵ 四边形ABCD 是正方形,
∵AE=CF=2,∴OA-AE=OC-CF=2,∴OE=OF=2.
又∵OB=OD,EF⊥BD,∴ 四边形BEDF 是菱形, ∴ BE = DE = DF = BF.
在 Rt△ODE 中,DE = ∴ 四边形 BEDF 的周长为
7. 【点拨】在 AD 上取一点 M,使得 AM =2,易知点 F,M关于直线 AC 对称.
连接EM ,交 AC 于点P',连接P'F,易得 即 EM 的长为PF +PE的最小值.
过点M作MN⊥BC 于点N,由题意易知EN=BN - BE=AM- BE=2-1 =1,MN=4,所以
点易错 此类问题容易出错的地方是不能将两条线段的长度和转化为一条线段的长度.
8. A 【点拨】在正方形ABCD中,AD=AB,∠BAD=∠ABC=∠ADC=90°.
将△ADF 绕点 A顺时针旋转90°,得 △ABG,则 AF = AG, ∠DAF = ∠BAG.
∵∠EAF=45°,∴ ∠BAE +∠DAF =45°,∴∠BAE+∠BAG=45°,即∠GAE=45°,
∴∠GAE =∠FAE.
在△GAE 和△FAE 中 △FAE(SAS),∴∠AEF=∠AEG.
∵∠BAE=α,∴∠AEB=90°-α,∴∠AEF =∠AEB =90°-α,
∴∠FEC=180°-∠AEF-∠AEB=180°-2×(90°-α) =2α.
9. B 【点拨】过点 D作DE⊥x轴于点 E,
∵ 四边形ABCD 是 正 方 形, ∴AB= AD, ∠BAD = 90°.
∵∠AOB=90°,∴ ∠BAO +∠DAO = ∠ABO +∠BAO = 90°, ∴ ∠ABO = ∠DAO.
∵ ∠AOB =∠DEA=90°,∴△ABO≌△DAE(AAS),∴DE=OA,AE=OB.
∵点A,B 的坐标分别为(a,0),(0,b), ∴OA=a,OB =b,∴ DE =a,AE =b,∴OE =b-a,
∴顶点 D 的坐标为(a-b,-a).
10.1 【点拨】连接AG,EG,∵ 四边形 ABCD 是正方形,∴∠B=∠C=90°.
∵E 是 CD的中点,∴DE=CE=4,设 CG=x,则 BG=8-x.
∵ HG 垂直平分AE,∴ AG = EG. ∴ 根据勾股定理,得
即 解得 x =7,
∴BG=BC-CG=8-7=1.
11.5 【点拨】如图,过点 O 作OF⊥BC于点F,过点A 作AM⊥OF 于点M,
则∠OFC=∠OFB=∠AMF=∠AMO=90°.
又∵∠ACB =90°,∴ 四边形 F BACFM 是矩形,∴AM=CF,MF =AC=3.
∵四边形ABDE 为正方形,
又∵
是等腰直角三角形,
∵FM =4-3=1,∴BC=CF+BF=4+1=5.
12.(1)【解】
(2)【证明】由正方形的性质可知
连接 AC,设每个小正方形的边长为1,则
∴∴△ABC是等腰直角三角形,且∠ACB = 90°,∴∠ABC=45°,
∴∠ABC=∠A B C .
13.(1)【证明】∵ 四边形ABCD 是正方形,∴ AD=BC,∠DBC=∠ADB=45°.
∵CG∥AP,∴∠BGC=∠BFP.∵∠BFP=∠AFD,∴∠AFD=∠BGC.
在△ADF和△CBG中 ∴△ADF≌△CBG(AAS).
(2)【解】四边形 AGCF 是菱形. 理由如下:
连接AC,交 BD 于点 O.
∵ 四边形 ABCD 是正方形, ∴OA=OC,OB =OD,AC⊥BD.
由(1)知△ADF≌△CBG,∴DF=BG,∴OB-BG=OD-FD,∴OG=OF.
又∵OA=OC,∴四边形AGCF 为平行四边形.
∵AC⊥FG,∴四边形AGCF 是菱形.
14.【证明】(1)∵ 四边形ABCD 是正方形;
.
在△AOF和△BOE中,
(2)如图,在 BG上取一点 H,使连接OH,
∵ O 为BD的中点,∴ OH是的中位线,∥
∵四边形ABCD 是正方形,45°,
∴ ∠FOH = 45°.∴∠OCB =∠FOH.
∵ BG 平分
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
