人教版八年级数学下册18.2 特殊的平行四边形 课件 (共24张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.2 特殊的平行四边形 课件 (共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 423.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 20:11:16 | ||
图片预览





文档简介
(共24张PPT)
特殊的平行四边形(第五课时)
初中数学
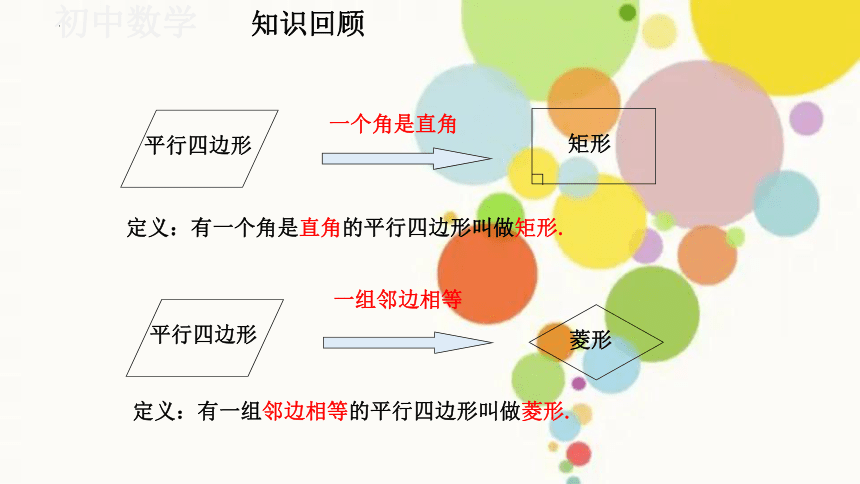
平行四边形
菱形
定义:有一组邻边相等的平行四边形叫做菱形.
一个角是直角
定义:有一个角是直角的平行四边形叫做矩形.
一组邻边相等
平行四边形
知识回顾
矩形
初中数学
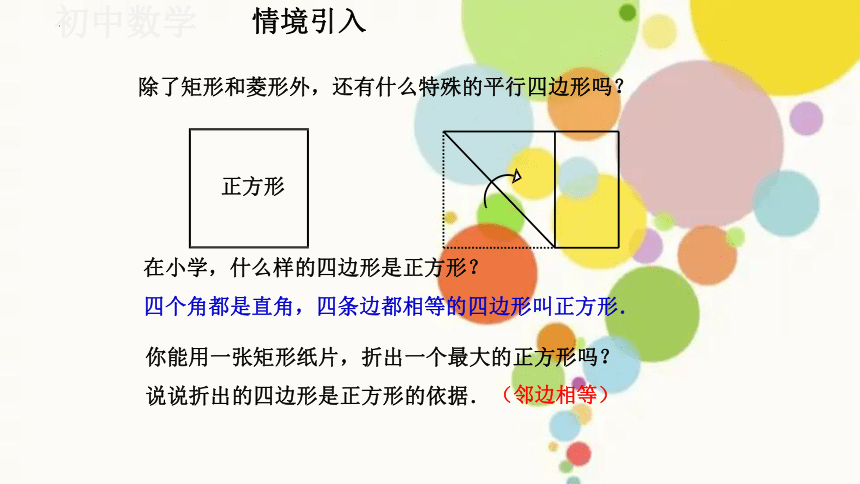
除了矩形和菱形外,还有什么特殊的平行四边形吗?
情境引入
正方形
在小学,什么样的四边形是正方形?
四个角都是直角,四条边都相等的四边形叫正方形.
你能用一张矩形纸片,折出一个最大的正方形吗? 说说折出的四边形是正方形的依据.(邻边相等)
初中数学
如图,某推拉门在完全关闭时,其相应的菱形变成正方形.
请说说图中∠1的变化过程.
1
1
情境引入
(由钝角变为直角)
初中数学
⑴有一组邻边相等的平行四边形(菱形)
⑵并且有一个角是直角的平行四边形(矩形)
两层 含义
正 方 形
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
理解定义
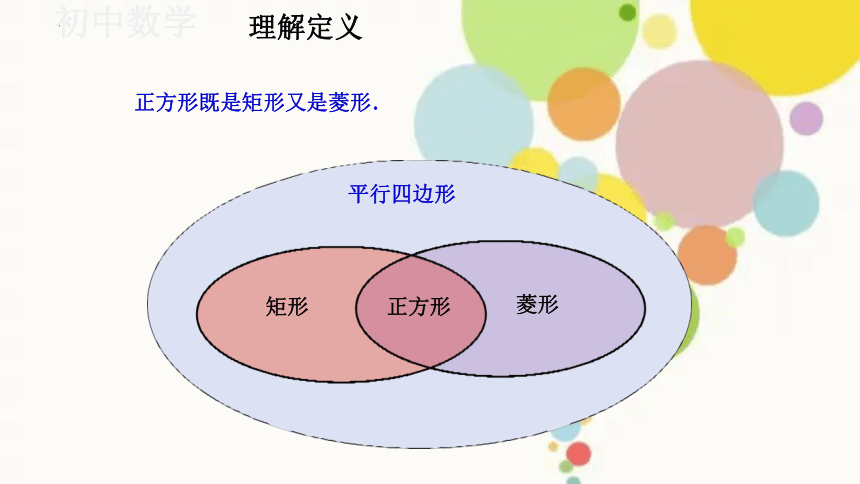
由正方形的定义可知:
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.
初中数学
矩形
菱形
正方形
平行四边形
理解定义
正方形既是矩形又是菱形.
初中数学
对角线
对角线相等
对角线互相垂直平分
每条对角线平分一组对角
正方形既是特殊的矩形,又是特殊的菱形.
正方形有哪些性质? 正方形具有矩形,菱形的所有性质. 对边平行
边
四边相等
角:四个角相等且都是直角
正方形的性质
探究性质
初中数学
正方形是轴对称图形吗?如果是,它的对称轴是什么?
探究性质
正方形是轴对称图形, 有四条对称轴,分别是 对角线所在直线,连接 对边中点的直线.
初中数学
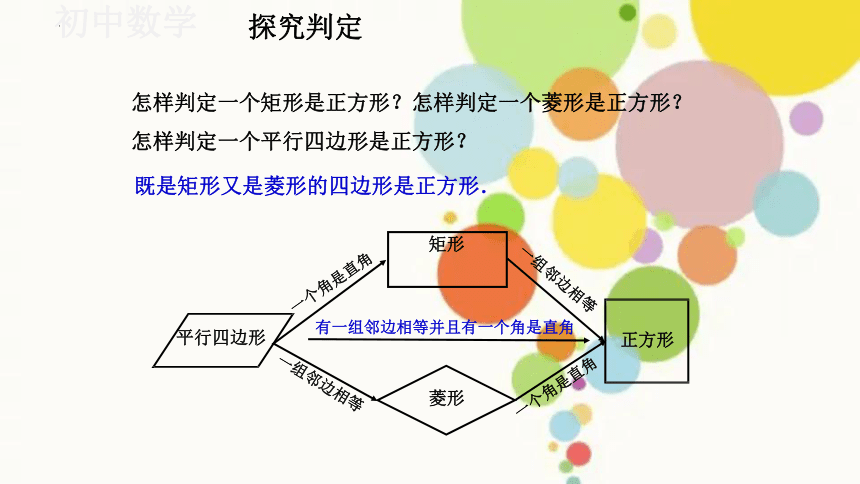
探究判定
一组邻边相等
平行四边形
菱形
一组邻边相等
一个角是直角
正方形
一个角是直角
有一组邻边相等并且有一个角是直角
怎样判定一个矩形是正方形?怎样判定一个菱形是正方形? 怎样判定一个平行四边形是正方形?
既是矩形又是菱形的四边形是正方形.
矩形
初中数学
对角线互相垂直
平行四边形
矩形
菱形
对角线互相垂直
对角线相等
正方形
对角线相等且互相垂直
既是矩形又是菱形的四边形是正方形.
探究判定
对角线相等
初中数学
例1 下列各句判定正方形的说法是否正确?
有一个角是直角的菱形是正方形.( )
有一组邻边相等的矩形是正方形. ( )
对角线相等的菱形是正方形.( )
对角线互相垂直的矩形是正方形. ( )
对角线相等且互相垂直的四边形是正方形.( )
运用判定
初中数学
运用判定
例1 下列各句判定正方形的说法是否正确?
有一个角是直角的菱形是正方形.( )
有一组邻边相等的矩形是正方形. ( )
对角线相等的菱形是正方形.( )
对角线互相垂直的矩形是正方形. ( )
对角线相等且互相垂直的四边形是正方形.( ) 对角线相等且互相垂直平分的四边形是正方形.
初中数学
例2 求证:正方形的两条对角线把这个正方形分成 四个全等的等腰直角三角形.
思考:判定一个三角形是等腰直角三角形需要什么条件? 判定两个三角形全等的条件又是什么?
运用性质
初中数学
分析:∵ 四边形ABCD是正方形,
∴ AC=BD, AC⊥BD,AO=CO=BO=DO.
∴ △ABO、△BCO、△CDO、△DAO 都是等腰直角三角形,
并且 △ABO ≌△BCO≌△CDO≌△DAO.
O
A
B
C
D
思考:图中共有多少个等腰直角三角形?
已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O. 求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
运用性质
初中数学
分析: ∵ 四边形ABCD是正方形,
∴ AC=BD, AC⊥BD,AO=CO=BO=DO.
∴ △ABO、△BCO、△CDO、△DAO 都是等腰直角三角形,
并且 △ABO ≌△BCO≌△CDO≌△DAO.
O
A
B
C
D
已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O. 求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
运用性质
思考:图中共有多少个等腰直角三角形?
8个,△ABO、△BCO、△CDO、△DAO、△ABD、△BCD、△ABC、△ACD.
初中数学
例3 在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O, 则△ABO的周长是 cm.
运用性质
初中数学
B
C
O
例3 在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O, 则△ABO的周长是 cm.
A D 略解:△ABO是等腰直角三角形,AB=12 cm,
利用勾股定理,可以求出OA=OB= 6 2 cm,
所以△ABO的周长是(12 12 2 )cm.
运用性质
初中数学
例4 如图,正方形ABCD中,对角线的交点为O,
E是OB上的一点,DG⊥AE于G,DG交OA于F. 求证:OE=OF.
运用性质
O
G
F
D
C
B
A
E
初中数学
∴ ∠AOE=∠DOF=90°,AO=DO.
又
∴
∴
∴
DG⊥AE, ∴∠EAO+∠AEO=∠EDG+∠AEO=90°.
∠EAO=∠FDO.
△AEO ≌△DFO(ASA).
OE=OF.
证明: ∵ 四边形ABCD是正方形,
运用性质
O
G
F
例4 如图,正方形ABCD中,对角线的交点为O, D
E是OB上的一点,DG⊥AE于G,DG交OA于F. 求证:OE=OF.
C
B
A
E
初中数学
例5 如图,四边形ABCD是正方形,分别 过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1 于N,直线BM、DN分别交l2于Q、P点.
求证:四边形PQMN是正方形.
运用判定
P C Q l2
D
B
l1
N A M
初中数学
证 明 : ∵ PN⊥l1,QM⊥l1,
∴ ∠PNM=∠QMN=90°,
∴ ∠PNM+∠QMN=180°,
∴ PN∥QM.
∵ l1∥l2, 即 PQ∥NM,
∴ 四边形PQMN是矩形.
运用判定
P C Q l2
D
B
l1
N A M
初中数学
运用判定
∵ 四边形ABCD是正方形,
∴ ∠BAD=∠ADC=90°,AB=AD=DC,
∴ ∠BAM+∠DAN=90°. 又 ∠ADN+∠DAN=90°,
∴ ∠BAM=∠ADN.
∴ △BAM ≌△ADN(AAS).
∴ AM=DN. 同理可证 AN=DP.
∴ AM+AN=DN+DP, 即 MN=PN.
∴ 四边形PQMN是正方形.
总结:先证出四边形PQMN是矩形,再证明一组邻边相等(MN=NP).
P C Q l2
D
B
l1
N A M
初中数学
正方形的概念、性质和判定
对角线
对角线相等
对角线互相垂直平分
每条对角线平分一组对角
课堂小结
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形既是特殊的矩形,又是特殊的菱形.具有矩形,菱形的所有性质. 对边平行
边
四边相等
角:四个角相等且都是直角
正方形的性质
正方形既是中心对称 图形也是轴对称图形, 有四条对称轴.
初中数学
一组邻边相等
平行四边形
3.既是矩形又是菱形的四边形是正方形.
矩形
菱形
一组邻边相等
一个角是直角
正方形
一个角是直角
有一组邻边相等并且有一个角是直角
正方形的概念、性质和判定
性质
定义
判定
逆向猜想
4.从一般到特殊的研究问题的方法.
特殊的平行四边形(第五课时)
初中数学
平行四边形
菱形
定义:有一组邻边相等的平行四边形叫做菱形.
一个角是直角
定义:有一个角是直角的平行四边形叫做矩形.
一组邻边相等
平行四边形
知识回顾
矩形
初中数学
除了矩形和菱形外,还有什么特殊的平行四边形吗?
情境引入
正方形
在小学,什么样的四边形是正方形?
四个角都是直角,四条边都相等的四边形叫正方形.
你能用一张矩形纸片,折出一个最大的正方形吗? 说说折出的四边形是正方形的依据.(邻边相等)
初中数学
如图,某推拉门在完全关闭时,其相应的菱形变成正方形.
请说说图中∠1的变化过程.
1
1
情境引入
(由钝角变为直角)
初中数学
⑴有一组邻边相等的平行四边形(菱形)
⑵并且有一个角是直角的平行四边形(矩形)
两层 含义
正 方 形
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
理解定义
由正方形的定义可知:
正方形既是有一组邻边相等的矩形,又是有一个角为直角的菱形.
初中数学
矩形
菱形
正方形
平行四边形
理解定义
正方形既是矩形又是菱形.
初中数学
对角线
对角线相等
对角线互相垂直平分
每条对角线平分一组对角
正方形既是特殊的矩形,又是特殊的菱形.
正方形有哪些性质? 正方形具有矩形,菱形的所有性质. 对边平行
边
四边相等
角:四个角相等且都是直角
正方形的性质
探究性质
初中数学
正方形是轴对称图形吗?如果是,它的对称轴是什么?
探究性质
正方形是轴对称图形, 有四条对称轴,分别是 对角线所在直线,连接 对边中点的直线.
初中数学
探究判定
一组邻边相等
平行四边形
菱形
一组邻边相等
一个角是直角
正方形
一个角是直角
有一组邻边相等并且有一个角是直角
怎样判定一个矩形是正方形?怎样判定一个菱形是正方形? 怎样判定一个平行四边形是正方形?
既是矩形又是菱形的四边形是正方形.
矩形
初中数学
对角线互相垂直
平行四边形
矩形
菱形
对角线互相垂直
对角线相等
正方形
对角线相等且互相垂直
既是矩形又是菱形的四边形是正方形.
探究判定
对角线相等
初中数学
例1 下列各句判定正方形的说法是否正确?
有一个角是直角的菱形是正方形.( )
有一组邻边相等的矩形是正方形. ( )
对角线相等的菱形是正方形.( )
对角线互相垂直的矩形是正方形. ( )
对角线相等且互相垂直的四边形是正方形.( )
运用判定
初中数学
运用判定
例1 下列各句判定正方形的说法是否正确?
有一个角是直角的菱形是正方形.( )
有一组邻边相等的矩形是正方形. ( )
对角线相等的菱形是正方形.( )
对角线互相垂直的矩形是正方形. ( )
对角线相等且互相垂直的四边形是正方形.( ) 对角线相等且互相垂直平分的四边形是正方形.
初中数学
例2 求证:正方形的两条对角线把这个正方形分成 四个全等的等腰直角三角形.
思考:判定一个三角形是等腰直角三角形需要什么条件? 判定两个三角形全等的条件又是什么?
运用性质
初中数学
分析:∵ 四边形ABCD是正方形,
∴ AC=BD, AC⊥BD,AO=CO=BO=DO.
∴ △ABO、△BCO、△CDO、△DAO 都是等腰直角三角形,
并且 △ABO ≌△BCO≌△CDO≌△DAO.
O
A
B
C
D
思考:图中共有多少个等腰直角三角形?
已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O. 求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
运用性质
初中数学
分析: ∵ 四边形ABCD是正方形,
∴ AC=BD, AC⊥BD,AO=CO=BO=DO.
∴ △ABO、△BCO、△CDO、△DAO 都是等腰直角三角形,
并且 △ABO ≌△BCO≌△CDO≌△DAO.
O
A
B
C
D
已知:如图,四边形ABCD是正方形,对角线AC、BD相交于点O. 求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.
运用性质
思考:图中共有多少个等腰直角三角形?
8个,△ABO、△BCO、△CDO、△DAO、△ABD、△BCD、△ABC、△ACD.
初中数学
例3 在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O, 则△ABO的周长是 cm.
运用性质
初中数学
B
C
O
例3 在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O, 则△ABO的周长是 cm.
A D 略解:△ABO是等腰直角三角形,AB=12 cm,
利用勾股定理,可以求出OA=OB= 6 2 cm,
所以△ABO的周长是(12 12 2 )cm.
运用性质
初中数学
例4 如图,正方形ABCD中,对角线的交点为O,
E是OB上的一点,DG⊥AE于G,DG交OA于F. 求证:OE=OF.
运用性质
O
G
F
D
C
B
A
E
初中数学
∴ ∠AOE=∠DOF=90°,AO=DO.
又
∴
∴
∴
DG⊥AE, ∴∠EAO+∠AEO=∠EDG+∠AEO=90°.
∠EAO=∠FDO.
△AEO ≌△DFO(ASA).
OE=OF.
证明: ∵ 四边形ABCD是正方形,
运用性质
O
G
F
例4 如图,正方形ABCD中,对角线的交点为O, D
E是OB上的一点,DG⊥AE于G,DG交OA于F. 求证:OE=OF.
C
B
A
E
初中数学
例5 如图,四边形ABCD是正方形,分别 过点A、C两点作l1∥l2,作BM⊥l1于M,DN⊥l1 于N,直线BM、DN分别交l2于Q、P点.
求证:四边形PQMN是正方形.
运用判定
P C Q l2
D
B
l1
N A M
初中数学
证 明 : ∵ PN⊥l1,QM⊥l1,
∴ ∠PNM=∠QMN=90°,
∴ ∠PNM+∠QMN=180°,
∴ PN∥QM.
∵ l1∥l2, 即 PQ∥NM,
∴ 四边形PQMN是矩形.
运用判定
P C Q l2
D
B
l1
N A M
初中数学
运用判定
∵ 四边形ABCD是正方形,
∴ ∠BAD=∠ADC=90°,AB=AD=DC,
∴ ∠BAM+∠DAN=90°. 又 ∠ADN+∠DAN=90°,
∴ ∠BAM=∠ADN.
∴ △BAM ≌△ADN(AAS).
∴ AM=DN. 同理可证 AN=DP.
∴ AM+AN=DN+DP, 即 MN=PN.
∴ 四边形PQMN是正方形.
总结:先证出四边形PQMN是矩形,再证明一组邻边相等(MN=NP).
P C Q l2
D
B
l1
N A M
初中数学
正方形的概念、性质和判定
对角线
对角线相等
对角线互相垂直平分
每条对角线平分一组对角
课堂小结
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形.
正方形既是特殊的矩形,又是特殊的菱形.具有矩形,菱形的所有性质. 对边平行
边
四边相等
角:四个角相等且都是直角
正方形的性质
正方形既是中心对称 图形也是轴对称图形, 有四条对称轴.
初中数学
一组邻边相等
平行四边形
3.既是矩形又是菱形的四边形是正方形.
矩形
菱形
一组邻边相等
一个角是直角
正方形
一个角是直角
有一组邻边相等并且有一个角是直角
正方形的概念、性质和判定
性质
定义
判定
逆向猜想
4.从一般到特殊的研究问题的方法.
