4.3 余角和补角
图片预览



文档简介
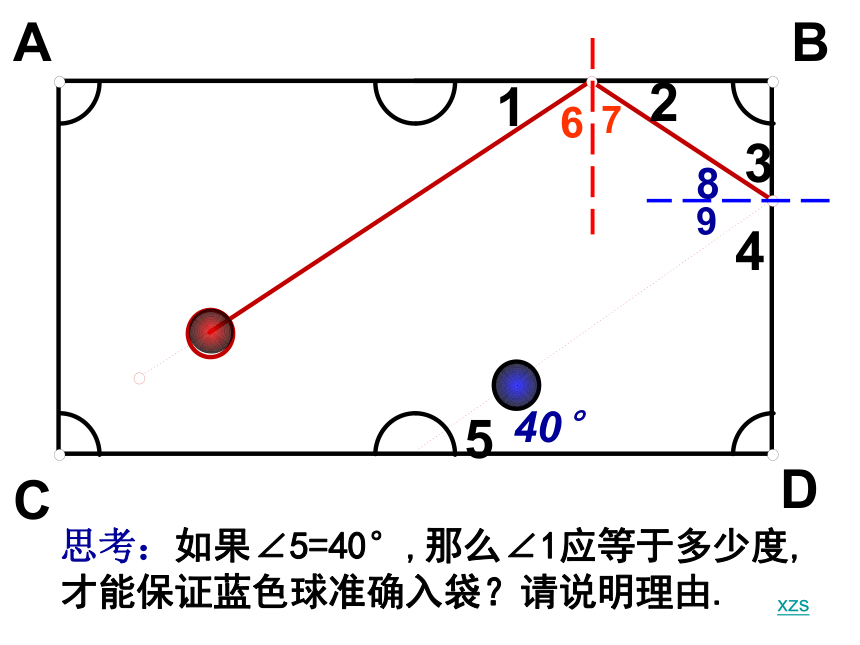
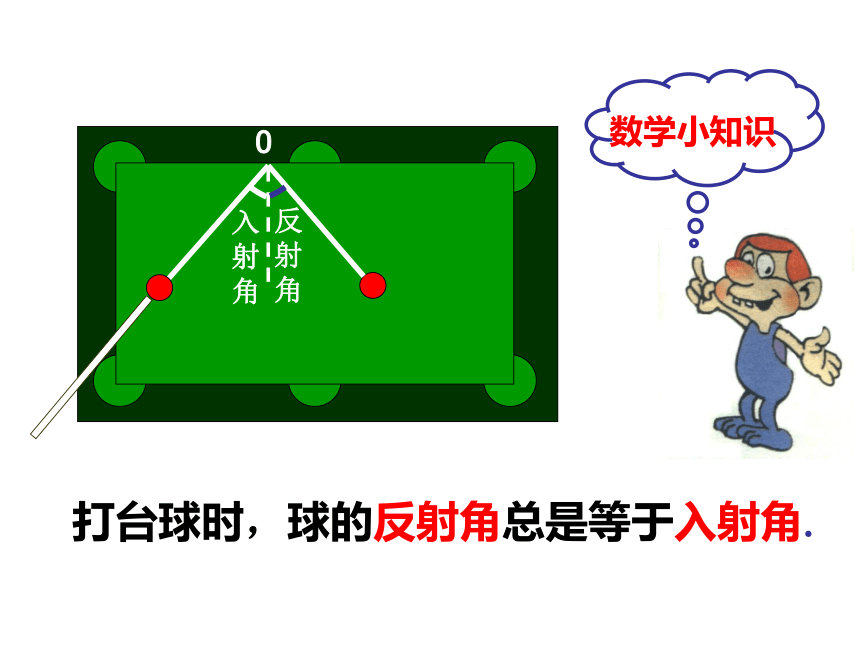
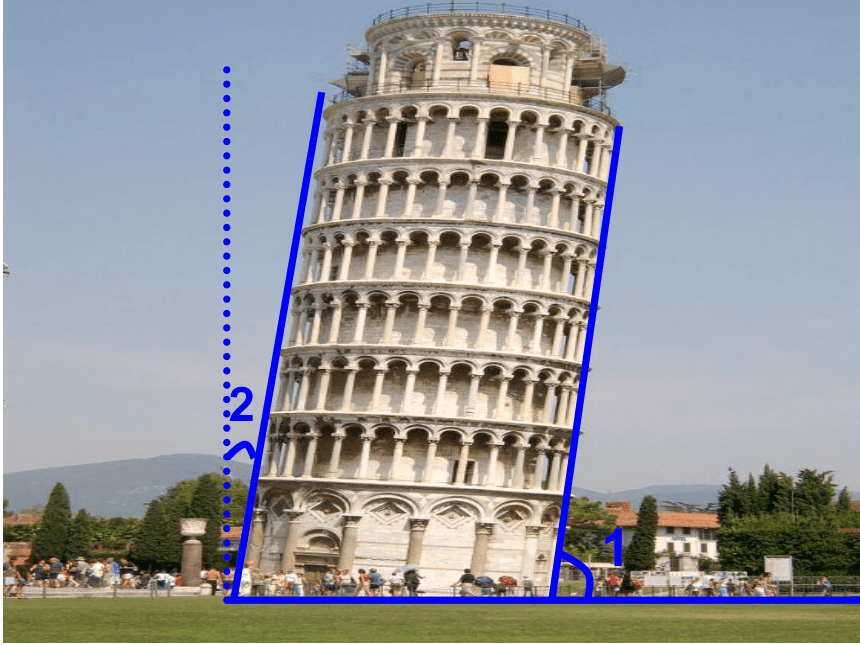
课件33张PPT。3.4.2余角与补角4.3余角与补角授课人:沈海尉思考:如果∠5=40°,那么∠1应等于多少度,才能保证蓝色球准确入袋?请说明理由.xzs40°打台球时,球的反射角总是等于入射角.O122
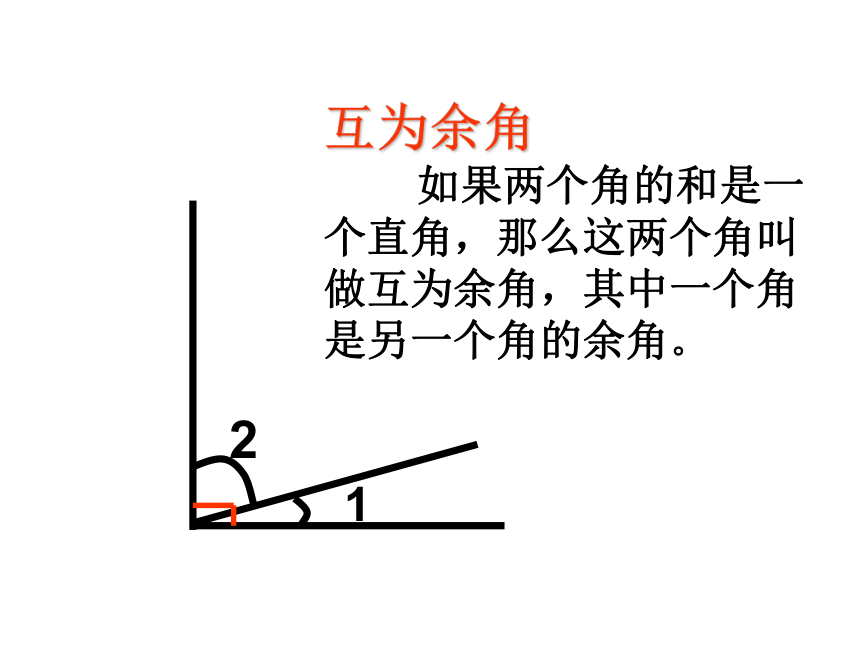
112互为余角
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
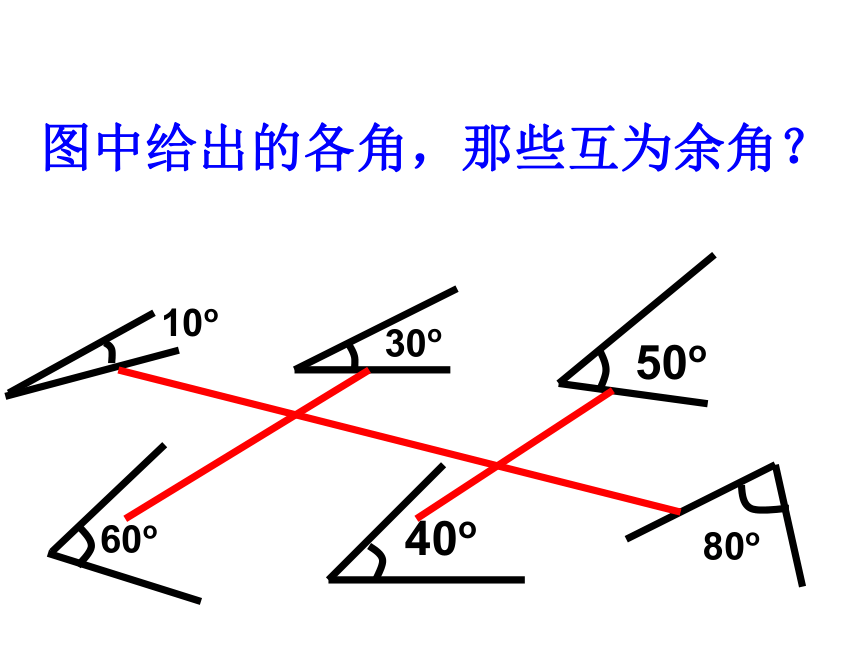
图中给出的各角,那些互为余角?10o30o60o80o50o40o343434互为补角
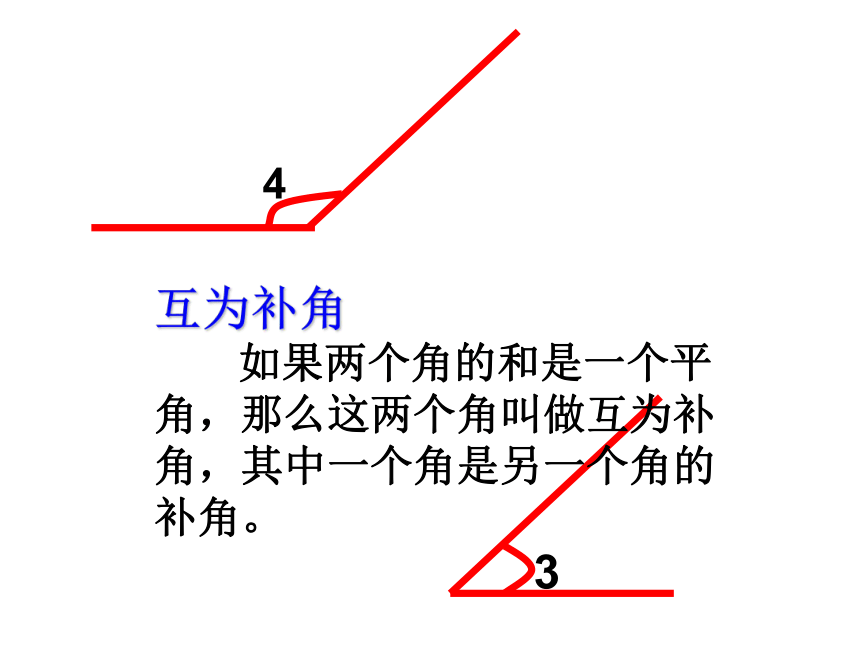
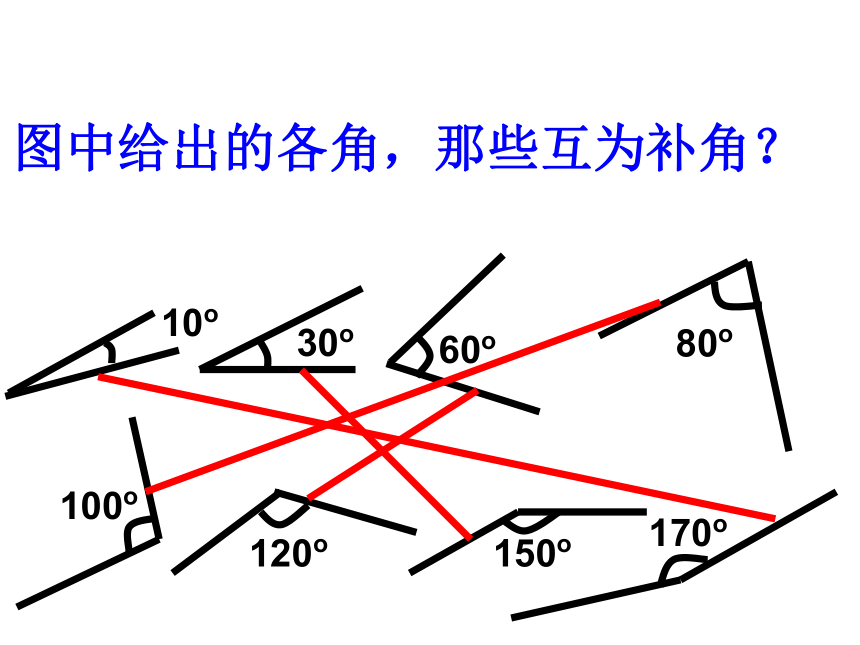
如果两个角的和是一个平角,那么这两个角叫做互为补角,其中一个角是另一个角的补角。
图中给出的各角,那些互为补角?10o30o60o80o100o120o150o170o问题3:互为余角、互为补角的两个角是否一定有公共顶点? 问题1:以上定义中的“互为”是什么意思?我来试一试:27°37′117°37′85°175°58°148°45°135°103°13°练习
一、填空
1、70°的余角是 ,补角是 。
2、 ∠ ? ( ∠ ? <90 ° )的余角是 ,它的补角是 。
110 °20°90°- ∠ ? 180°- ∠ ? 重要提醒:(如何表示一个角的余角和补角)
锐角∠?的余角是(90 °—∠ ? )
∠?的补角是(180 °—∠ ? )想一想:1、钝角有余角吗?没有 2、直角有余角吗?没有 3、同一个角的补角比它的余角大多少度?90°(3)如果一个角的余角和补角都存在,那么这
个角的余角一定比这个角的补角小.(2)如果两个角互补,那么这两个角中,一个
是锐角,另一个是钝角;(1)一个锐角的补角一定是钝角;1、判断下列说法是否正确,并说明理由.√√注意:1、只有锐角有余角;
2、一个角的余角与它的补角相差90°.三.活学活用.加深理解1、90度的角叫余角,180度的角叫补角。 ( )3、如果一个角有补角,那么这个角一定是钝角。( )(一)判断题:4、互补的两个角不可能相等。 ( )5、钝角没有余角,但一定有补角。( )6、互余的两个角一定都是锐角,两个锐角一定互余.( )????????例1 若一个角的补角等于它的余角的4 倍, 求这个角的度数。解: 设这个角是x °,则它的补角是 ( 180°-x°),余角是(90°-x°) 。
根据题意得:
(180°-x°)= 4 (90°-x°)
解得: x =60
答:这个角的度数是60 °。(2)如果∠1的补角是∠1的3倍,求∠1的度数。(3)、已知两个角互为补角,它们的差30°, 求这两个角的度数。
总结:
1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。3、同一个角的补角比余角大90度。∠1与∠2互余, ∠3与∠4互余,如果∠1=∠3,
那么∠2与∠4相等吗?为什么?分析:由题意可知 ∠2=90°- ∠1, ∠4=90°- ∠3答:∠2 =∠4 ,因为 ∠1 =∠3,
所以90°- ∠1 =90°- ∠3(等量减等量差相等)你能得到什么结论吗?等角的余角相等∠1与∠2互补, ∠3与∠4互补,如果∠1=∠3,
那么∠2与∠4相等吗?为什么?答:∠2 =∠4 ,因为 ∠1 =∠3,
所以180°- ∠1 =180°- ∠3(等量减等量差相等)你能得到什么结论吗?等角的补角相等例2、如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗?_________.
图中有哪些角相等?∠2,∠4∠3,∠1∠BOD等角的补角相等,等角的余角相等. 如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?B东西北南O(1)正东,正南,正西,正北(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OAABCDOBOCOD45°射线OE射线OF射线OG射线OH45°45°45°O北南西东 (3)南偏西25°25° 北偏西70° 南偏东60°射线OA射线OB射线OC70°60°甲地乙地乙地对甲地的方位角1. 先找出中心点,然后画出方向指标甲地乙地乙地对甲地的方位角2. 把中心点和目的地用线连接起來甲地乙地乙地对甲地的方位角3.度量向北的射线和蓝色线之间的角度北 ● 本节课你学到了哪些知识? ● 通过这节课的学习后,你有什么感受? 小结∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等。同角或等角的补角相等。
112互为余角
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
图中给出的各角,那些互为余角?10o30o60o80o50o40o343434互为补角
如果两个角的和是一个平角,那么这两个角叫做互为补角,其中一个角是另一个角的补角。
图中给出的各角,那些互为补角?10o30o60o80o100o120o150o170o问题3:互为余角、互为补角的两个角是否一定有公共顶点? 问题1:以上定义中的“互为”是什么意思?我来试一试:27°37′117°37′85°175°58°148°45°135°103°13°练习
一、填空
1、70°的余角是 ,补角是 。
2、 ∠ ? ( ∠ ? <90 ° )的余角是 ,它的补角是 。
110 °20°90°- ∠ ? 180°- ∠ ? 重要提醒:(如何表示一个角的余角和补角)
锐角∠?的余角是(90 °—∠ ? )
∠?的补角是(180 °—∠ ? )想一想:1、钝角有余角吗?没有 2、直角有余角吗?没有 3、同一个角的补角比它的余角大多少度?90°(3)如果一个角的余角和补角都存在,那么这
个角的余角一定比这个角的补角小.(2)如果两个角互补,那么这两个角中,一个
是锐角,另一个是钝角;(1)一个锐角的补角一定是钝角;1、判断下列说法是否正确,并说明理由.√√注意:1、只有锐角有余角;
2、一个角的余角与它的补角相差90°.三.活学活用.加深理解1、90度的角叫余角,180度的角叫补角。 ( )3、如果一个角有补角,那么这个角一定是钝角。( )(一)判断题:4、互补的两个角不可能相等。 ( )5、钝角没有余角,但一定有补角。( )6、互余的两个角一定都是锐角,两个锐角一定互余.( )????????例1 若一个角的补角等于它的余角的4 倍, 求这个角的度数。解: 设这个角是x °,则它的补角是 ( 180°-x°),余角是(90°-x°) 。
根据题意得:
(180°-x°)= 4 (90°-x°)
解得: x =60
答:这个角的度数是60 °。(2)如果∠1的补角是∠1的3倍,求∠1的度数。(3)、已知两个角互为补角,它们的差30°, 求这两个角的度数。
总结:
1、互为余角(互余)、互为补角(互补)是两个角之间的数量关系,不是位置关系。2、互为余角的两个角不一定是直角中分成的两个角,互为补角的两个角不一定是平角中分成的两个角。3、同一个角的补角比余角大90度。∠1与∠2互余, ∠3与∠4互余,如果∠1=∠3,
那么∠2与∠4相等吗?为什么?分析:由题意可知 ∠2=90°- ∠1, ∠4=90°- ∠3答:∠2 =∠4 ,因为 ∠1 =∠3,
所以90°- ∠1 =90°- ∠3(等量减等量差相等)你能得到什么结论吗?等角的余角相等∠1与∠2互补, ∠3与∠4互补,如果∠1=∠3,
那么∠2与∠4相等吗?为什么?答:∠2 =∠4 ,因为 ∠1 =∠3,
所以180°- ∠1 =180°- ∠3(等量减等量差相等)你能得到什么结论吗?等角的补角相等例2、如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗?_________.
图中有哪些角相等?∠2,∠4∠3,∠1∠BOD等角的补角相等,等角的余角相等. 如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?B东西北南O(1)正东,正南,正西,正北(2)西北方向:_________
西南方向:__________
东南方向:__________
东北方向:__________
射线OAABCDOBOCOD45°射线OE射线OF射线OG射线OH45°45°45°O北南西东 (3)南偏西25°25° 北偏西70° 南偏东60°射线OA射线OB射线OC70°60°甲地乙地乙地对甲地的方位角1. 先找出中心点,然后画出方向指标甲地乙地乙地对甲地的方位角2. 把中心点和目的地用线连接起來甲地乙地乙地对甲地的方位角3.度量向北的射线和蓝色线之间的角度北 ● 本节课你学到了哪些知识? ● 通过这节课的学习后,你有什么感受? 小结∠1+ ∠2 = 90 °∠1+ ∠2 = 180 °同角或等角的余角相等。同角或等角的补角相等。
