2009年福建省文科数学高考样卷
图片预览


文档简介
2009年福建省高考数学文科样卷
第I卷(选择题共60分)
选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
复数等于 A. B. C. D.
已知全集U={-1,0,1,2},集合A={-1,2},B={0,2},则等于 A. {0} B.{2} C. {0,1,2} D.
已知是定义在上的奇函数,当时,,则等于 A.3 B.-3 C.6 D.-6
命题“对任意的”的否定是 A.不存在 B.存在 C.存在 D.对任意的
曲线在点处的切线的倾斜角为( )
A.30° B.45° C.60° D.120°
已知直线和两个不同的平面、,则下列命题正确的是 A. 若,,则// B. 若//, //,则// C. 若,,则// D. 若//,,则
对于右边的程序框图,当输入的值是5,则输出的值是
A. 0.2 B. 0.3 C. 0.5 D. 1
△ABC的内角A、B、C所对的边分别为a、b、c,若sinA=,b=sinB,则a等于 A. B. C. D.
已知向量a=(2,1),b=(3,2),若a(a+b),则实数等于 A. B. C. D.
在某五场篮球比赛中,甲、乙两名运动员得分的茎叶图如右.下列说法正确的是 A.在这五场比赛中,甲的平均得分比乙好,且甲比乙稳定 B.在这五场比赛中,甲的平均得分比乙好,但乙比甲稳定 C.在这五场比赛中,乙的平均得分比甲好,且乙比甲稳定 D.在这五场比赛中,乙的平均得分比甲好,但甲比乙稳定
已知圆的方程为.设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为
A.10 B.20 C.30 D.40
已知函数,正实数、、满足,若实数是函数的一个零点,那么下列四个判断:
①;②;③;④.
其中可能成立的个数为
A.1 B.2 C.3 D.4
第II卷(非选择题共90分)
填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
双曲线的焦距为 .
由x,y满足的约束条件,作出可行域如图中阴影部分(含边界)所示,则目标函数z=3x+y的最大值是________.
若函数,(0,+∞)的值恒大于4,则实数m的取值范围是_______.
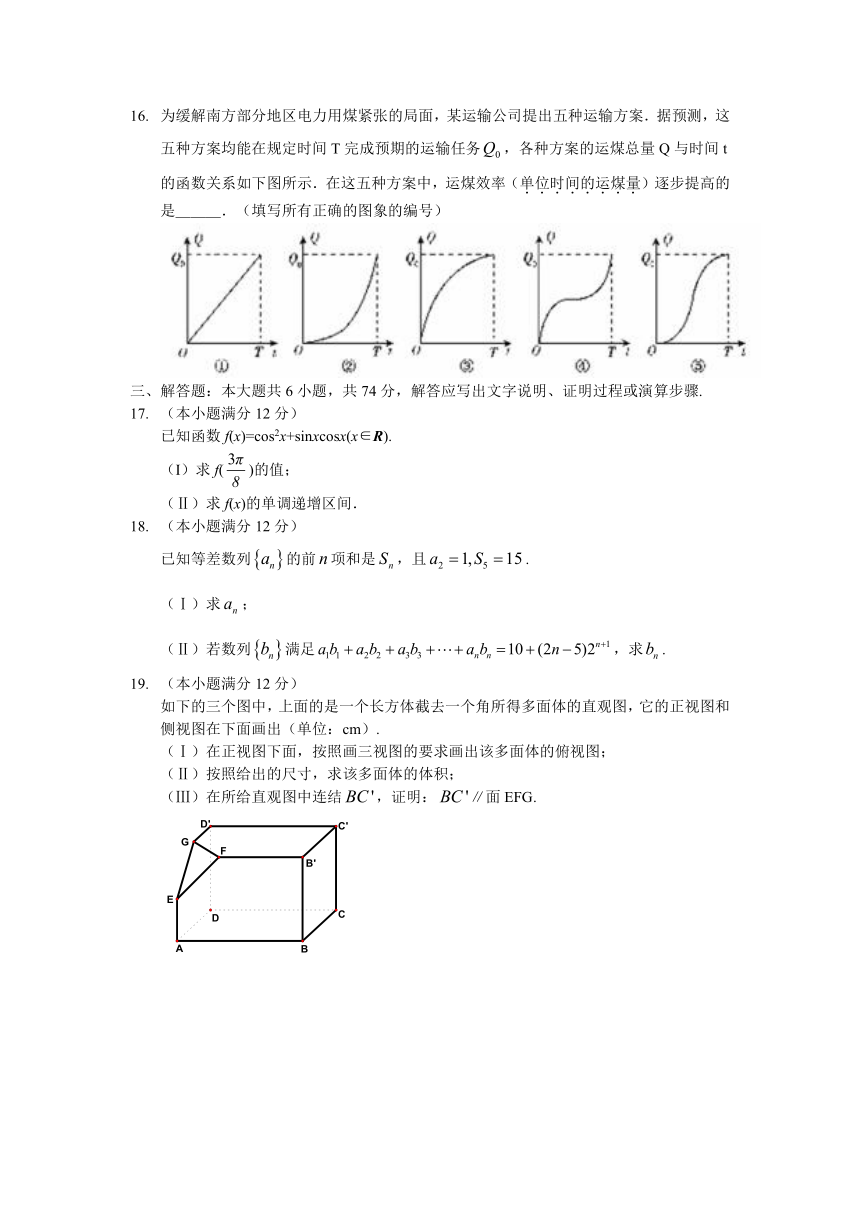
为缓解南方部分地区电力用煤紧张的局面,某运输公司提出五种运输方案.据预测,这五种方案均能在规定时间T完成预期的运输任务,各种方案的运煤总量Q与时间t的函数关系如下图所示.在这五种方案中,运煤效率(单位时间的运煤量)逐步提高的是___.(填写所有正确的图象的编号)
解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
(本小题满分12分) 已知函数f(x)=cos2x+sinxcosx(x∈R). (I)求f()的值; (Ⅱ)求f(x)的单调递增区间.
(本小题满分12分) 已知等差数列的前项和是,且. (Ⅰ)求; (Ⅱ)若数列满足,求.
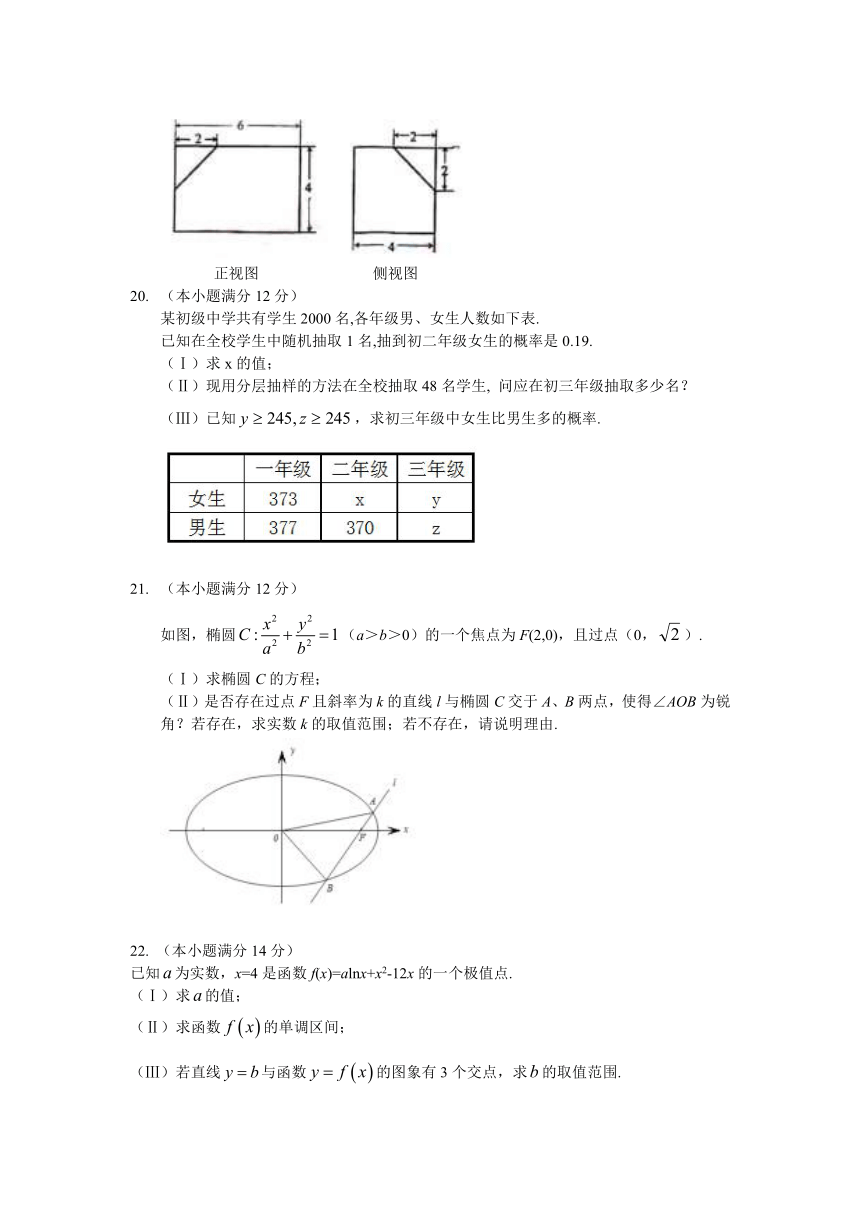
(本小题满分12分) 如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm). (Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (Ⅱ)按照给出的尺寸,求该多面体的体积; (Ⅲ)在所给直观图中连结,证明:∥面EFG. 正视图 侧视图
(本小题满分12分) 某初级中学共有学生2000名,各年级男、女生人数如下表. 已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19. (Ⅰ)求x的值; (Ⅱ)现用分层抽样的方法在全校抽取48名学生, 问应在初三年级抽取多少名? (Ⅲ)已知,求初三年级中女生比男生多的概率.
(本小题满分12分) 如图,椭圆(a>b>0)的一个焦点为F(2,0),且过点(0,). (Ⅰ)求椭圆C的方程; (Ⅱ)是否存在过点F且斜率为k的直线l与椭圆C交于A、B两点,使得∠AOB为锐角?若存在,求实数k的取值范围;若不存在,请说明理由.
22. (本小题满分14分) 已知为实数,x=4是函数f(x)=alnx+x2-12x的一个极值点. (Ⅰ)求的值; (Ⅱ)求函数的单调区间; (Ⅲ)若直线与函数的图象有3个交点,求的取值范围. 参考答案
一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分.
1.D. 2.A. 3.B. 4.C. 5.B. 6.A.
7.C. 8.D. 9.D. 10.C. 11.B. 12.B.
二、填空题:本题考查基础知识和基本运算,每小题4分,满分16分.
13.. 14.5. 15.或. 16.②.
三、解答题:本大题共6小题,共74分.解答应写出文字说明.证明过程或演算步骤.
17.本题主要考查两角和与差的三角函数公式、二倍角公式,三角函数的图象与性质等基础知识;考查运算求解能力.满分12分.
.
,
,
即时,f(x)单调递增.
∴f(x)的单调递增区间为[,].
18.本题主要考查等差数列、数列求和等基础知识;考查推理论证与运算求解能力;考查化归与转化思想.满分12分.
(Ⅰ)设数列{an}的公差为d,则 解得.
因此,an=-1+2(n-1)=2n-3. (Ⅱ)由已知 (1)得,
当n≥2时, (2).
由(1)-(2)得,
所以,又,
故.
在式(1)中,令n=1得,,
又,故.
所以.
19.本题主要考查空间几何体的直观图、三视图,空间线面的位置关系等基础知识;考查空间想像能力及推理论证能力.满分12分. (Ⅰ)如图 俯视图 (Ⅱ)所求多面体的体积 . (Ⅲ)证明:如图,在长方体中,连接,则∥. 因为E,G分别为的中点, 所以∥,从而∥. 又,所以∥平面EFG.
20.本题主要考查概率与统计的基础知识,考查运算求解能力及应用意识.满分12分.
(Ⅰ)由,解得. (Ⅱ)初三年级人数为, 设应在初三年级抽取m人,则,解得m=12. 所以应在初三年级抽取12名. (Ⅲ)设初三年级女生比男生多的事件为,初三年级女生和男生数记为数对, 由(Ⅱ)知,则基本事件总数有: 共11个, 而事件包含的基本事件有: 共5个, 所以.
21.本题主要考查直线与椭圆的位置关系等基础知识;考查运算求解能力及化归与转化思想.满分12分. (Ⅰ)由题设b=,c=2,从而a2=b2+c2=6, 所以椭圆C的方程为.
(Ⅱ)假设斜率为k的直线l与椭圆C交于A、B两点,使得∠AOB为锐角,
设直线l的方程为y=k(x - 2).
所以满足题意的的直线l存在,斜率k的取值范围为
方法二: 同方法一得到.
所以满足题意的的直线l存在,斜率k的取值范围为
22.本题主要考查利用导数研究函数的性质,考查运算求解能力及数形结合思想.满分14分. (Ⅰ),由得, ,解得. (Ⅱ)由(Ⅰ)知, , . 当时,; 当时,;
时,. 所以的单调增区间是;的单调减区间是. (Ⅲ)由(Ⅱ)知,在内单调递增,在内单调递减,在上单调递增,且当或时,. 所以的极大值为,极小值为. 又因为, .
当且仅当,直线与的图象有三个交点. 所以,的取值范围为.
第I卷(选择题共60分)
选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
复数等于 A. B. C. D.
已知全集U={-1,0,1,2},集合A={-1,2},B={0,2},则等于 A. {0} B.{2} C. {0,1,2} D.
已知是定义在上的奇函数,当时,,则等于 A.3 B.-3 C.6 D.-6
命题“对任意的”的否定是 A.不存在 B.存在 C.存在 D.对任意的
曲线在点处的切线的倾斜角为( )
A.30° B.45° C.60° D.120°
已知直线和两个不同的平面、,则下列命题正确的是 A. 若,,则// B. 若//, //,则// C. 若,,则// D. 若//,,则
对于右边的程序框图,当输入的值是5,则输出的值是
A. 0.2 B. 0.3 C. 0.5 D. 1
△ABC的内角A、B、C所对的边分别为a、b、c,若sinA=,b=sinB,则a等于 A. B. C. D.
已知向量a=(2,1),b=(3,2),若a(a+b),则实数等于 A. B. C. D.
在某五场篮球比赛中,甲、乙两名运动员得分的茎叶图如右.下列说法正确的是 A.在这五场比赛中,甲的平均得分比乙好,且甲比乙稳定 B.在这五场比赛中,甲的平均得分比乙好,但乙比甲稳定 C.在这五场比赛中,乙的平均得分比甲好,且乙比甲稳定 D.在这五场比赛中,乙的平均得分比甲好,但甲比乙稳定
已知圆的方程为.设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为
A.10 B.20 C.30 D.40
已知函数,正实数、、满足,若实数是函数的一个零点,那么下列四个判断:
①;②;③;④.
其中可能成立的个数为
A.1 B.2 C.3 D.4
第II卷(非选择题共90分)
填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
双曲线的焦距为 .
由x,y满足的约束条件,作出可行域如图中阴影部分(含边界)所示,则目标函数z=3x+y的最大值是________.
若函数,(0,+∞)的值恒大于4,则实数m的取值范围是_______.
为缓解南方部分地区电力用煤紧张的局面,某运输公司提出五种运输方案.据预测,这五种方案均能在规定时间T完成预期的运输任务,各种方案的运煤总量Q与时间t的函数关系如下图所示.在这五种方案中,运煤效率(单位时间的运煤量)逐步提高的是___.(填写所有正确的图象的编号)
解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤.
(本小题满分12分) 已知函数f(x)=cos2x+sinxcosx(x∈R). (I)求f()的值; (Ⅱ)求f(x)的单调递增区间.
(本小题满分12分) 已知等差数列的前项和是,且. (Ⅰ)求; (Ⅱ)若数列满足,求.
(本小题满分12分) 如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位:cm). (Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图; (Ⅱ)按照给出的尺寸,求该多面体的体积; (Ⅲ)在所给直观图中连结,证明:∥面EFG. 正视图 侧视图
(本小题满分12分) 某初级中学共有学生2000名,各年级男、女生人数如下表. 已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19. (Ⅰ)求x的值; (Ⅱ)现用分层抽样的方法在全校抽取48名学生, 问应在初三年级抽取多少名? (Ⅲ)已知,求初三年级中女生比男生多的概率.
(本小题满分12分) 如图,椭圆(a>b>0)的一个焦点为F(2,0),且过点(0,). (Ⅰ)求椭圆C的方程; (Ⅱ)是否存在过点F且斜率为k的直线l与椭圆C交于A、B两点,使得∠AOB为锐角?若存在,求实数k的取值范围;若不存在,请说明理由.
22. (本小题满分14分) 已知为实数,x=4是函数f(x)=alnx+x2-12x的一个极值点. (Ⅰ)求的值; (Ⅱ)求函数的单调区间; (Ⅲ)若直线与函数的图象有3个交点,求的取值范围. 参考答案
一、选择题:本题考查基础知识和基本运算,每小题5分,满分60分.
1.D. 2.A. 3.B. 4.C. 5.B. 6.A.
7.C. 8.D. 9.D. 10.C. 11.B. 12.B.
二、填空题:本题考查基础知识和基本运算,每小题4分,满分16分.
13.. 14.5. 15.或. 16.②.
三、解答题:本大题共6小题,共74分.解答应写出文字说明.证明过程或演算步骤.
17.本题主要考查两角和与差的三角函数公式、二倍角公式,三角函数的图象与性质等基础知识;考查运算求解能力.满分12分.
.
,
,
即时,f(x)单调递增.
∴f(x)的单调递增区间为[,].
18.本题主要考查等差数列、数列求和等基础知识;考查推理论证与运算求解能力;考查化归与转化思想.满分12分.
(Ⅰ)设数列{an}的公差为d,则 解得.
因此,an=-1+2(n-1)=2n-3. (Ⅱ)由已知 (1)得,
当n≥2时, (2).
由(1)-(2)得,
所以,又,
故.
在式(1)中,令n=1得,,
又,故.
所以.
19.本题主要考查空间几何体的直观图、三视图,空间线面的位置关系等基础知识;考查空间想像能力及推理论证能力.满分12分. (Ⅰ)如图 俯视图 (Ⅱ)所求多面体的体积 . (Ⅲ)证明:如图,在长方体中,连接,则∥. 因为E,G分别为的中点, 所以∥,从而∥. 又,所以∥平面EFG.
20.本题主要考查概率与统计的基础知识,考查运算求解能力及应用意识.满分12分.
(Ⅰ)由,解得. (Ⅱ)初三年级人数为, 设应在初三年级抽取m人,则,解得m=12. 所以应在初三年级抽取12名. (Ⅲ)设初三年级女生比男生多的事件为,初三年级女生和男生数记为数对, 由(Ⅱ)知,则基本事件总数有: 共11个, 而事件包含的基本事件有: 共5个, 所以.
21.本题主要考查直线与椭圆的位置关系等基础知识;考查运算求解能力及化归与转化思想.满分12分. (Ⅰ)由题设b=,c=2,从而a2=b2+c2=6, 所以椭圆C的方程为.
(Ⅱ)假设斜率为k的直线l与椭圆C交于A、B两点,使得∠AOB为锐角,
设直线l的方程为y=k(x - 2).
所以满足题意的的直线l存在,斜率k的取值范围为
方法二: 同方法一得到.
所以满足题意的的直线l存在,斜率k的取值范围为
22.本题主要考查利用导数研究函数的性质,考查运算求解能力及数形结合思想.满分14分. (Ⅰ),由得, ,解得. (Ⅱ)由(Ⅰ)知, , . 当时,; 当时,;
时,. 所以的单调增区间是;的单调减区间是. (Ⅲ)由(Ⅱ)知,在内单调递增,在内单调递减,在上单调递增,且当或时,. 所以的极大值为,极小值为. 又因为, .
当且仅当,直线与的图象有三个交点. 所以,的取值范围为.
同课章节目录
