新课标人教A版 选修2-1 2.2.2椭圆的简单几何性质(1)
文档属性
| 名称 | 新课标人教A版 选修2-1 2.2.2椭圆的简单几何性质(1) |  | |
| 格式 | rar | ||
| 文件大小 | 72.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-03 23:42:00 | ||
图片预览



文档简介
(共13张PPT)
2.2.2 椭圆的简单几何性质(一)
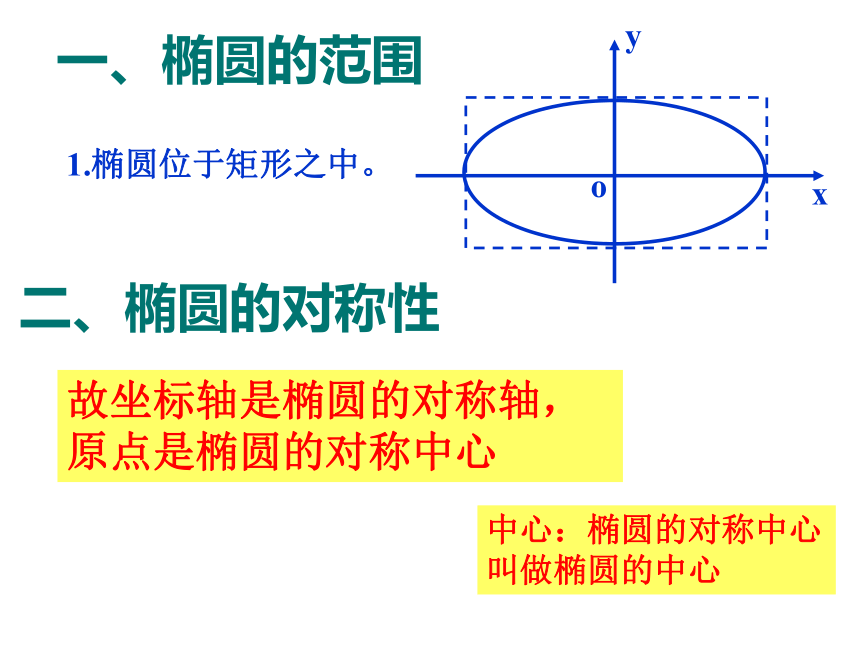
一、椭圆的范围
o
x
y
1.椭圆位于矩形之中。
二、椭圆的对称性
故坐标轴是椭圆的对称轴,原点是椭圆的对称中心
中心:椭圆的对称中心叫做椭圆的中心
三、椭圆的顶点
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和
短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。
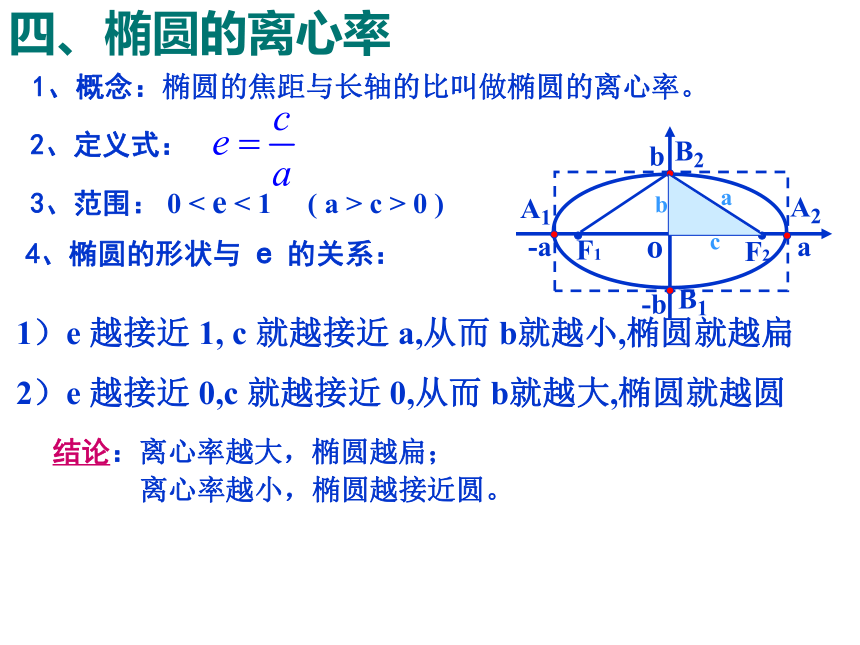
四、椭圆的离心率
1、概念:椭圆的焦距与长轴的比叫做椭圆的离心率。
3、范围: 0 < e < 1 ( a > c > 0 )
4、椭圆的形状与 e 的关系:
2、定义式:
结论:离心率越大,椭圆越扁;
离心率越小,椭圆越接近圆。
o
F1
F2
c
a
b
B2
B1
A2
-a
a
A1
-b
b
1)e 越接近 1, c 就越接近 a,从而 b就越小,椭圆就越扁
2)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆
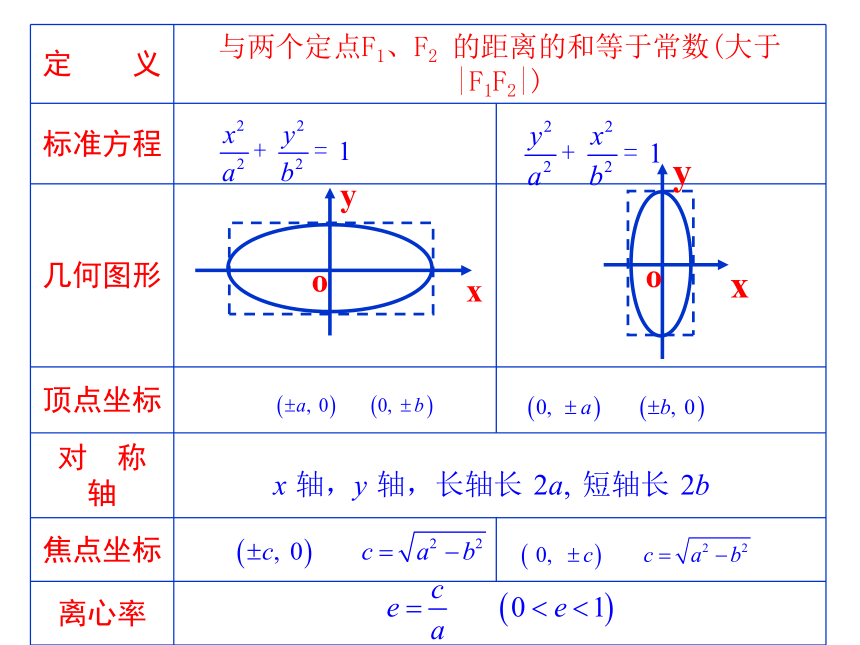
定 义 与两个定点F1、F2 的距离的和等于常数(大于|F1F2|)
标准方程
几何图形
顶点坐标
对 称 轴
焦点坐标
离心率
o
x
y
o
x
y
例4
求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标
解:把已知方程化成标准方程
这里,
因此,椭圆的长轴长和短轴长分别是
离心率
焦点坐标分别是
四个顶点坐标是
F2
补充题:如图,我国发射的第一颗人造地球卫星的运行轨道,是以地心(地球的中心)F2为一个焦点的椭圆.已知它的近地点A(离地面最近的点)距地面439km,远地点B(离地面最远的点)距地面2384km,并且F2、A、B在同一直线上,地球半径约为6371km.求卫星运行的轨道方程(精确到1km).
F1
x
y
0
A
B
a
a
c
解:如图,建立直角坐标系,使点A、B、F2在x轴上,F2为椭圆的右焦点(记F1为左焦点).
因为椭圆的焦点在x轴上,所以设它的标准方程为
F2
则 a-c=|OA|-|OF2|=|F2A|
=6371+439=6810,
a+c=|OB|+|OF2|=|F2B|
=6371+2384=8755.
解得 a=7782.5,c=972.5.
∴b=√a2-c2=√(a+c)(a-c)
=√8755×6810.
≈7722.
∴ 卫星的轨道方程是
F2
F1
x
y
0
A
B
a
a
c
F2
练习1:求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 。
练习2:已知椭圆中心在原点,对称轴为坐标轴,焦点在y轴,长轴是短轴的2倍,焦距为2,离心率为 ,求椭圆的方程。
x
y
解析:由题可得:设椭圆方程为:
又
椭圆方程为:
练习3:已知椭圆的中心在原点,一个顶点和一个焦点分
别是直线 x + 3y –6=0与两坐标轴的交点,求它的标
准方程。
解:
如右图所示,若A(6,0)为顶点,B(0, 2)为焦点,
x
所以椭圆的标准方程为
A(6, 0)
B(0, 2)
y
0
x
x
则b=6 , c=2, a2=b2+c2=40. 此时椭圆的标准方程为
2.2.2 椭圆的简单几何性质(一)
一、椭圆的范围
o
x
y
1.椭圆位于矩形之中。
二、椭圆的对称性
故坐标轴是椭圆的对称轴,原点是椭圆的对称中心
中心:椭圆的对称中心叫做椭圆的中心
三、椭圆的顶点
o
x
y
B1(0,b)
B2(0,-b)
A1
A2
顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和
短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。
四、椭圆的离心率
1、概念:椭圆的焦距与长轴的比叫做椭圆的离心率。
3、范围: 0 < e < 1 ( a > c > 0 )
4、椭圆的形状与 e 的关系:
2、定义式:
结论:离心率越大,椭圆越扁;
离心率越小,椭圆越接近圆。
o
F1
F2
c
a
b
B2
B1
A2
-a
a
A1
-b
b
1)e 越接近 1, c 就越接近 a,从而 b就越小,椭圆就越扁
2)e 越接近 0,c 就越接近 0,从而 b就越大,椭圆就越圆
定 义 与两个定点F1、F2 的距离的和等于常数(大于|F1F2|)
标准方程
几何图形
顶点坐标
对 称 轴
焦点坐标
离心率
o
x
y
o
x
y
例4
求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标
解:把已知方程化成标准方程
这里,
因此,椭圆的长轴长和短轴长分别是
离心率
焦点坐标分别是
四个顶点坐标是
F2
补充题:如图,我国发射的第一颗人造地球卫星的运行轨道,是以地心(地球的中心)F2为一个焦点的椭圆.已知它的近地点A(离地面最近的点)距地面439km,远地点B(离地面最远的点)距地面2384km,并且F2、A、B在同一直线上,地球半径约为6371km.求卫星运行的轨道方程(精确到1km).
F1
x
y
0
A
B
a
a
c
解:如图,建立直角坐标系,使点A、B、F2在x轴上,F2为椭圆的右焦点(记F1为左焦点).
因为椭圆的焦点在x轴上,所以设它的标准方程为
F2
则 a-c=|OA|-|OF2|=|F2A|
=6371+439=6810,
a+c=|OB|+|OF2|=|F2B|
=6371+2384=8755.
解得 a=7782.5,c=972.5.
∴b=√a2-c2=√(a+c)(a-c)
=√8755×6810.
≈7722.
∴ 卫星的轨道方程是
F2
F1
x
y
0
A
B
a
a
c
F2
练习1:求适合下列条件的椭圆的标准方程:
(1)经过点P(-3,0),Q(0,-2);
(2)长轴长等于20,离心率等于 。
练习2:已知椭圆中心在原点,对称轴为坐标轴,焦点在y轴,长轴是短轴的2倍,焦距为2,离心率为 ,求椭圆的方程。
x
y
解析:由题可得:设椭圆方程为:
又
椭圆方程为:
练习3:已知椭圆的中心在原点,一个顶点和一个焦点分
别是直线 x + 3y –6=0与两坐标轴的交点,求它的标
准方程。
解:
如右图所示,若A(6,0)为顶点,B(0, 2)为焦点,
x
所以椭圆的标准方程为
A(6, 0)
B(0, 2)
y
0
x
x
则b=6 , c=2, a2=b2+c2=40. 此时椭圆的标准方程为
