1.1周期变化 课件(共15张PPT)
文档属性
| 名称 | 1.1周期变化 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 872.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 21:15:38 | ||
图片预览





文档简介
(共15张PPT)
第一章 三角函数
§1 周期变化
周期变化
正弦函数
余弦函数
正弦函数和余
弦函数的概念
正弦函数和余
弦函数的图象
及性质
y=Asin(ωx+φ)
函数y=Asin(ωx+φ)
的图象及性质
函数图象的平移和
伸缩变化
角的概念
任意角
弧度制
三角函数的简单应用
正切函数
三角函数
本章概述
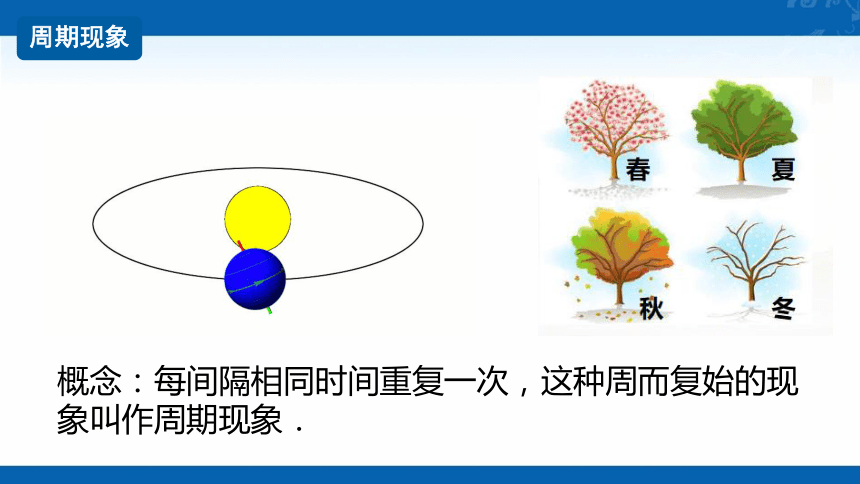
▲地球公转引起的
四季更替
▲星期制、二十四小时制
的使用
“周而复始”、“循环往复”
春分
夏至
秋分
冬至
导入新课
概念:每间隔相同时间重复一次,这种周而复始的现象叫作周期现象.
周期现象
练习1:下列现象不是周期现象的是( )
A.春去春又回
B.钟表的分针每小时转一圈
C.天干地支表示年、月、日的时间顺序
D.某交通路口每次绿灯通过的车辆数
解析:由周期现象的概念易知,A,B,C都是周期现象,某交通路口每次绿灯通过的车辆数不是周期现象,故选D.
答案:D
练习2:下列现象是周期现象的是( )
①日出日落 ②潮汐 ③海啸 ④地震
A.①② B.①②③
C.①②④ D.③④
解析: 显然日出日落和潮汐是周期现象.故选A.
答案:A
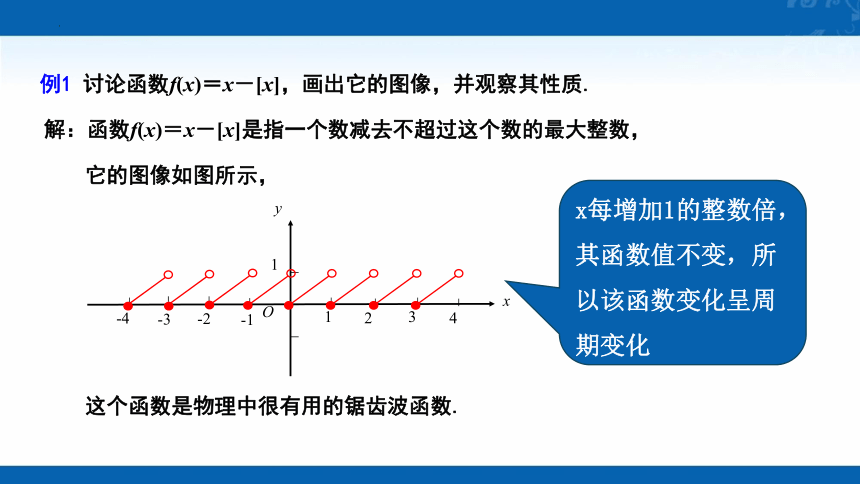
例1 讨论函数f(x)=x-[x],画出它的图像,并观察其性质.
解:函数f(x)=x-[x]是指一个数减去不超过这个数的最大整数,
O
1
y
1
x
-1
-2
-3
-4
2
3
4
它的图像如图所示,
这个函数是物理中很有用的锯齿波函数.
x每增加1的整数倍,其函数值不变,所以该函数变化呈周期变化
例2 讨论函数f(x)=的图像和性质.
解:
当[]为偶数时,函数f(x)==1;
当[x]为奇数时,函数f(x)==-1.
在平面直角坐标系中,该函数的图像
如图所示.
O
1
y
1
x
-1
-2
-3
-4
-5
2
3
4
5
-1
x每增加2的整数倍,其函数值不变,呈周期性变化
O
1
y
1
x
-1
-2
-3
-4
-5
2
3
4
5
-1
概念生成
O
1
y
1
x
-1
-2
-3
-4
2
3
4
x每增加2的整数倍,其函数值不变
x每增加1的整数倍,其函数值不变
思考:如何用数学符号语言描述这一性质?
概念生成
一般地,对于函数y=f(x),x∈D,如果存在一个非零常数T,使得对任意的x∈D,都有x+T∈D且满足
f(x+T)=f(x),
那么函数y=f(x)称作周期函数,非零常数T 称作这个函数的周期.
思考:对于函数,满足,那么6是该函数周期吗?
思考:对于函数,存在满足,那么6是该函数周期吗?
思考:周期函数的周期是否唯一?
周期函数的周期不止一个.
如果在周期函数y=f(x)的所有周期中存在一个最小的正数, 那么这个最小正数就称作函数y=f(x)的最小正周期.
注意:若不加特别说明,本书所指周期均为函数的最小正周期.
O
1
y
1
x
-1
-2
-3
-4
2
3
4
O
1
y
1
x
-1
-2
-3
-4
-5
2
3
4
5
-1
例3 讨论函数y=7+(-1)n,n∈N是否为周期函数,如果是,请指出它的周期.
解:当n∈N时,该函数的取值为8,6,8,6,8,
可见它是周期函数,且周期T=2.
例4 如图是一个单摆振动的函数图象,那么单摆的振动函数图象是周期变化吗?若是周期变化,其振动的周期是多少?
解:观察图象可知,图象从t=0.8 s 开始重复,所以单摆的振动是周期变化.
振动的周期为0.8 s.
例5
思考:试画出该函数一个周期的图像.
例5 已知函数定义域为R,若其满足一下关系式,该函数是否为周期函数,若有则最小正周期为多少?
①
②
③
④
思考:结合例3-例5,求函数周期有什么方法?
课堂小结
生活中的
“周而复始”
周期函数的
定义
周期变化
函数图象的
“重复出现”
函数值满足
f (x +T )=f (x)
数学建模
直观想象
数学抽象
逻辑推理
课堂小结
第一章 三角函数
§1 周期变化
周期变化
正弦函数
余弦函数
正弦函数和余
弦函数的概念
正弦函数和余
弦函数的图象
及性质
y=Asin(ωx+φ)
函数y=Asin(ωx+φ)
的图象及性质
函数图象的平移和
伸缩变化
角的概念
任意角
弧度制
三角函数的简单应用
正切函数
三角函数
本章概述
▲地球公转引起的
四季更替
▲星期制、二十四小时制
的使用
“周而复始”、“循环往复”
春分
夏至
秋分
冬至
导入新课
概念:每间隔相同时间重复一次,这种周而复始的现象叫作周期现象.
周期现象
练习1:下列现象不是周期现象的是( )
A.春去春又回
B.钟表的分针每小时转一圈
C.天干地支表示年、月、日的时间顺序
D.某交通路口每次绿灯通过的车辆数
解析:由周期现象的概念易知,A,B,C都是周期现象,某交通路口每次绿灯通过的车辆数不是周期现象,故选D.
答案:D
练习2:下列现象是周期现象的是( )
①日出日落 ②潮汐 ③海啸 ④地震
A.①② B.①②③
C.①②④ D.③④
解析: 显然日出日落和潮汐是周期现象.故选A.
答案:A
例1 讨论函数f(x)=x-[x],画出它的图像,并观察其性质.
解:函数f(x)=x-[x]是指一个数减去不超过这个数的最大整数,
O
1
y
1
x
-1
-2
-3
-4
2
3
4
它的图像如图所示,
这个函数是物理中很有用的锯齿波函数.
x每增加1的整数倍,其函数值不变,所以该函数变化呈周期变化
例2 讨论函数f(x)=的图像和性质.
解:
当[]为偶数时,函数f(x)==1;
当[x]为奇数时,函数f(x)==-1.
在平面直角坐标系中,该函数的图像
如图所示.
O
1
y
1
x
-1
-2
-3
-4
-5
2
3
4
5
-1
x每增加2的整数倍,其函数值不变,呈周期性变化
O
1
y
1
x
-1
-2
-3
-4
-5
2
3
4
5
-1
概念生成
O
1
y
1
x
-1
-2
-3
-4
2
3
4
x每增加2的整数倍,其函数值不变
x每增加1的整数倍,其函数值不变
思考:如何用数学符号语言描述这一性质?
概念生成
一般地,对于函数y=f(x),x∈D,如果存在一个非零常数T,使得对任意的x∈D,都有x+T∈D且满足
f(x+T)=f(x),
那么函数y=f(x)称作周期函数,非零常数T 称作这个函数的周期.
思考:对于函数,满足,那么6是该函数周期吗?
思考:对于函数,存在满足,那么6是该函数周期吗?
思考:周期函数的周期是否唯一?
周期函数的周期不止一个.
如果在周期函数y=f(x)的所有周期中存在一个最小的正数, 那么这个最小正数就称作函数y=f(x)的最小正周期.
注意:若不加特别说明,本书所指周期均为函数的最小正周期.
O
1
y
1
x
-1
-2
-3
-4
2
3
4
O
1
y
1
x
-1
-2
-3
-4
-5
2
3
4
5
-1
例3 讨论函数y=7+(-1)n,n∈N是否为周期函数,如果是,请指出它的周期.
解:当n∈N时,该函数的取值为8,6,8,6,8,
可见它是周期函数,且周期T=2.
例4 如图是一个单摆振动的函数图象,那么单摆的振动函数图象是周期变化吗?若是周期变化,其振动的周期是多少?
解:观察图象可知,图象从t=0.8 s 开始重复,所以单摆的振动是周期变化.
振动的周期为0.8 s.
例5
思考:试画出该函数一个周期的图像.
例5 已知函数定义域为R,若其满足一下关系式,该函数是否为周期函数,若有则最小正周期为多少?
①
②
③
④
思考:结合例3-例5,求函数周期有什么方法?
课堂小结
生活中的
“周而复始”
周期函数的
定义
周期变化
函数图象的
“重复出现”
函数值满足
f (x +T )=f (x)
数学建模
直观想象
数学抽象
逻辑推理
课堂小结
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
