第六章 特殊平行四边形 单元检测题(含答案)
文档属性
| 名称 | 第六章 特殊平行四边形 单元检测题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 15:54:57 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第六章 特殊平行四边形
单元检测题
(时间:90分钟 满分:120分)
一、选择题(每题3分,共36分)
1.菱形、矩形、正方形都具有的性质是( )
A.四条边相等,四个角相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
2.在矩形ABCD中,对角线AC,BD相交于点O,若AC=16, 则OD等于( )
A.16 B.12 C.10 D.8
3.如图,菱形ABCD的对角线 AC 与BD相交于点O,若AB=5,AC=6,则BD 的长为( )
A.4 B.6 C.7 D.8
(第3 题) (第4 题)
4.如图,以正方形 ABCD 的对角线AC为一边作菱形AEFC,则∠FAB的度数是( )
A.20° B.30° C.50° D.22.5°
5.如图,DE 为△ABC 的中位线,点 F 在 DE 上,且∠AFB=90°,若AB =5,BC=8,则EF的长为( )
A.2 B.1.5 C.2.5 D.3
6.在四边形ABCD中,∠A=∠B=∠C=90°.如果再添加一个条件可推出四边形ABCD 是正方形,那么这个条件可以是( )
A. AB=CD B. BC=CD C.∠D=90° D. AC=BD
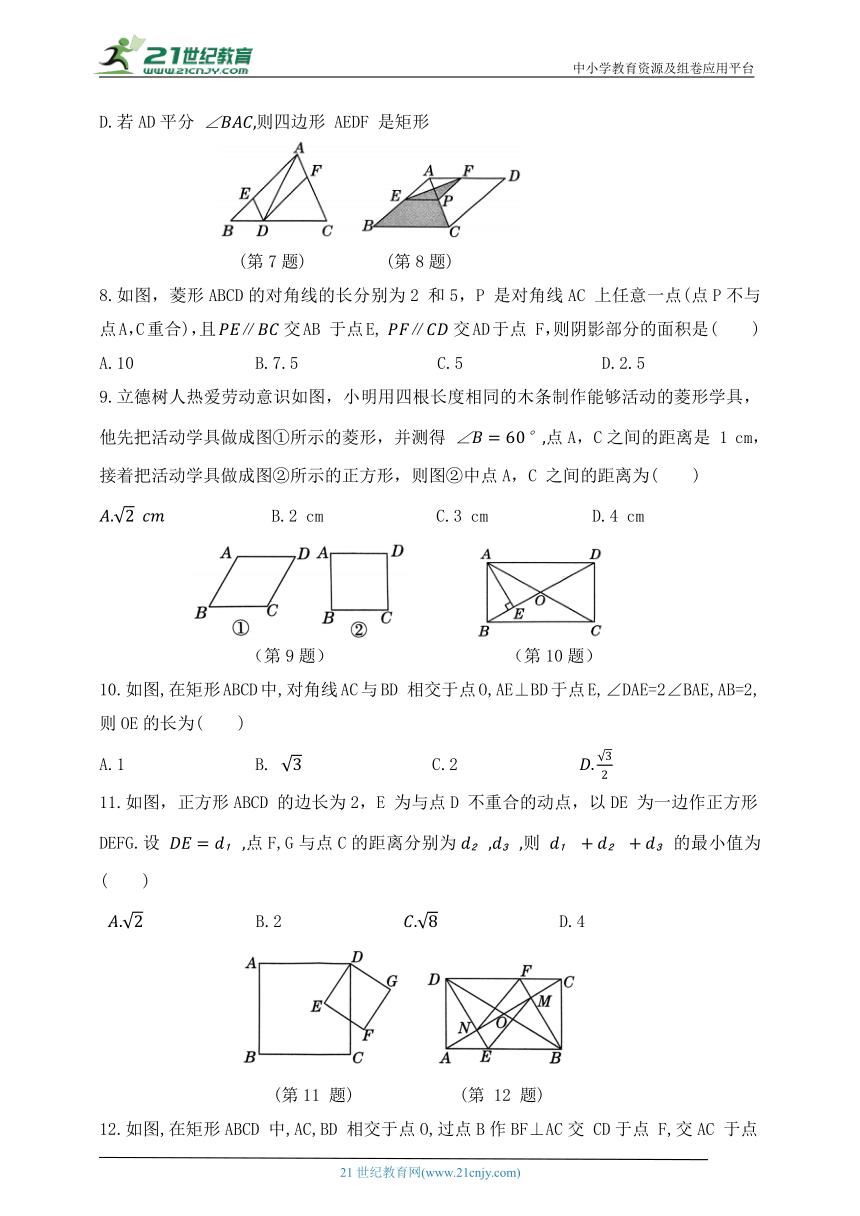
7.如图,在△ABC中,点D在BC上, DE∥AC,DF∥AB,下列四个判断中不正确的是( )
A.四边形AEDF 是平行四边形
B.若 则四边形AEDF 是矩形
C.若 且 则四边形 AEDF 是菱形
D.若AD平分 则四边形 AEDF 是矩形
(第7题) (第8题)
8.如图,菱形ABCD的对角线的长分别为2 和5,P 是对角线AC 上任意一点(点P不与点A,C重合),且∥交AB 于点E, ∥交AD于点 F,则阴影部分的面积是( )
A.10 B.7.5 C.5 D.2.5
9.立德树人热爱劳动意识如图,小明用四根长度相同的木条制作能够活动的菱形学具,他先把活动学具做成图①所示的菱形,并测得 点A,C之间的距离是 1 cm,接着把活动学具做成图②所示的正方形,则图②中点A,C 之间的距离为( )
B.2 cm C.3 cm D.4 cm
(第9题) (第10题)
10.如图,在矩形ABCD中,对角线AC与BD 相交于点O,AE⊥BD于点E,∠DAE=2∠BAE,AB=2,则OE的长为( )
A.1 B. C.2
11.如图,正方形ABCD 的边长为2,E 为与点D 不重合的动点,以DE 为一边作正方形DEFG.设 点F,G与点C的距离分别为则 的最小值为( )
B.2 D.4
(第11 题) (第 12 题)
12.如图,在矩形ABCD 中,AC,BD 相交于点O,过点B作BF⊥AC交 CD于点 F,交AC 于点M,过点 D作 DE∥BF 交 AB 于点 E,交 AC 于点 N,连接FN,EM.则下列结论:①DN= BM;②EM∥FN;③AE=CM;④当AO=AD时,四边形DEBF 是菱形.其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题3分,共18分)
13.如图,在菱形ABCD 中,E为 CD的中点,菱形ABCD的周长为32,则
(第13 题) (第14 题)
14.如图,在 中,D,E,F 分别是AB, BC 和AC边的中点,请添加一个条件:_________,使四边形BEFD为矩形.
15.如图,将正方形OACD 放在平面直角坐标系中,O 是坐标原点,点D的坐标为(3,4),则点A 的坐标为__________.
(第 15 题) (第 16题)
16.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD 中,对角线AC与BD 交于点O,点E 为BC 边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点 F,G,则EF +EG=____________.
17.如图,在△ABC 中, AD 是 的角平分线,分别以点A,D为圆心,大于 的长为半径作弧,两弧交于点 M,N,作直线 MN,分别交 AB,AC 于点E,F,连接DE,DF,若△CDF 的周长为 12,AC =8,则四边形AEDF 的面积为____________.
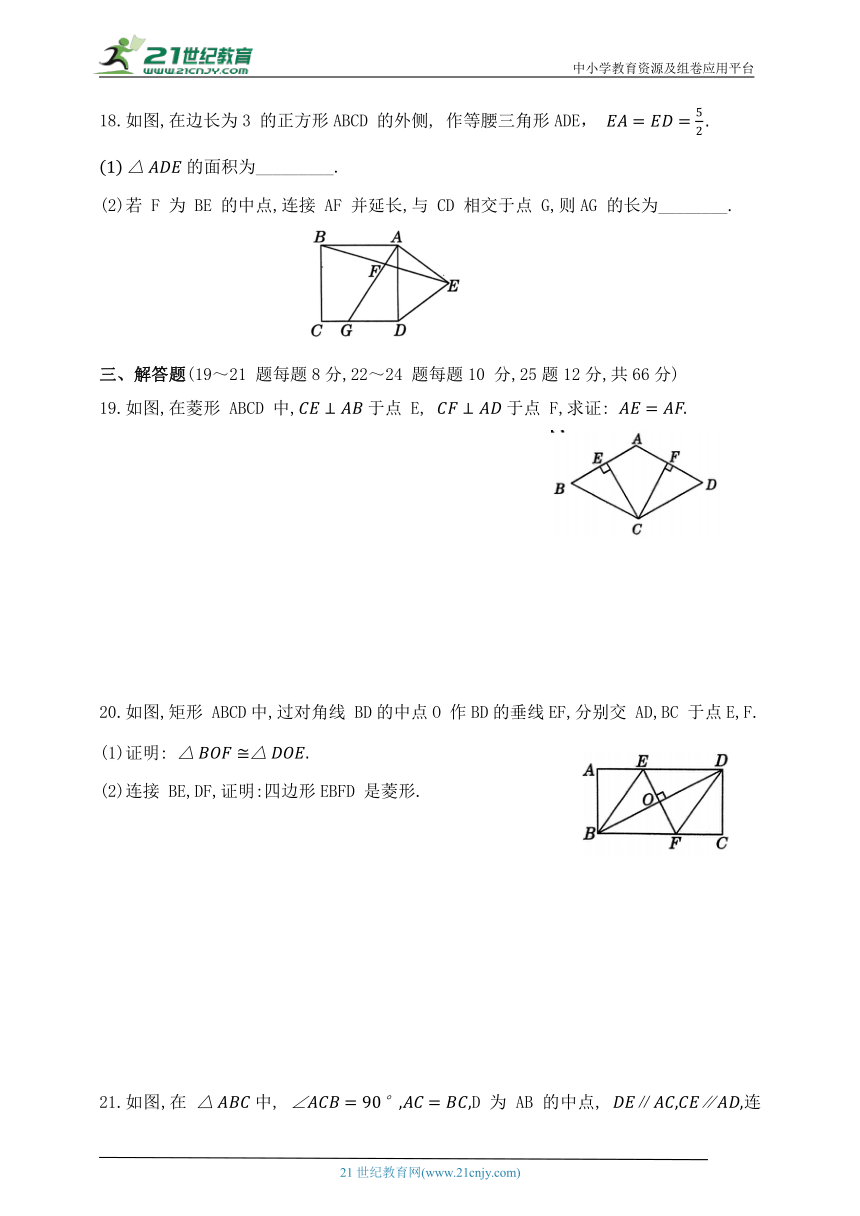
18.如图,在边长为3 的正方形ABCD 的外侧, 作等腰三角形ADE,
的面积为_________.
(2)若 F 为 BE 的中点,连接 AF 并延长,与 CD 相交于点 G,则AG 的长为________.
三、解答题(19~21 题每题8分,22~24 题每题10 分,25题12分,共66分)
19.如图,在菱形 ABCD 中,于点 E, 于点 F,求证:
20.如图,矩形 ABCD中,过对角线 BD的中点O 作BD的垂线EF,分别交 AD,BC 于点E,F.
(1)证明:
(2)连接 BE,DF,证明:四边形EBFD 是菱形.
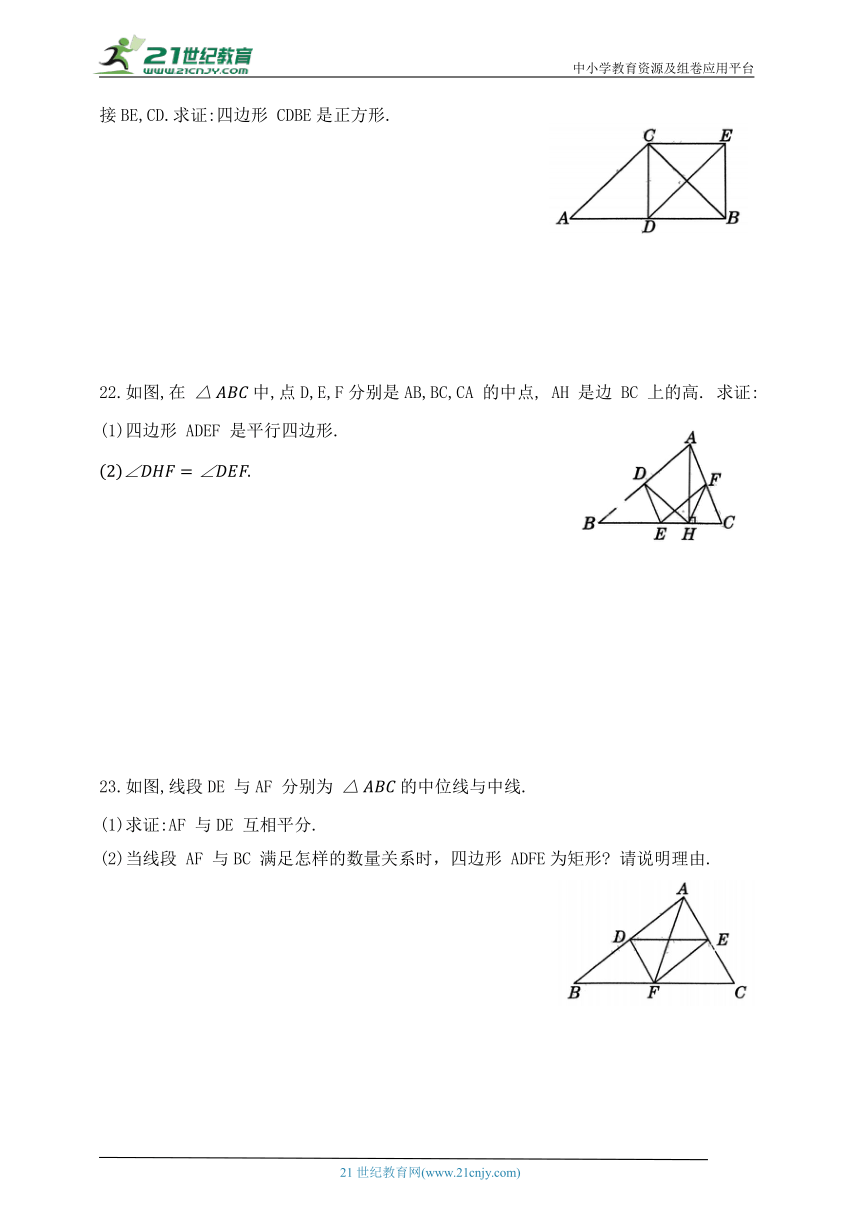
21.如图,在 中, D 为 AB 的中点, ∥∥连接BE,CD.求证:四边形 CDBE是正方形.
22.如图,在 中,点D,E,F分别是AB,BC,CA 的中点, AH 是边 BC 上的高. 求证:
(1)四边形 ADEF 是平行四边形.
23.如图,线段DE 与AF 分别为 的中位线与中线.
(1)求证:AF 与DE 互相平分.
(2)当线段 AF 与BC 满足怎样的数量关系时,四边形 ADFE为矩形 请说明理由.
24.如图,在矩形ABCD中,对角线AC 的垂直平分线分别与边AB 和边 CD 的延长线交于点M,N,与边 AD交于点E,垂足为点 O.
(1)求证:
(2)若 求AE 的长.
25.如图①,在正方形ABCD 中,点P 是对角线 BD上的一点, 点 E 在 AD 的延长线上,且. PE 交 CD于点 F,
(1)证明:
(2)求 的度数.
(3)如图②,把正方形ABCD 改为菱形ABCD,其他条件不变,连接 CE,当时,试探究线段 AP 与线段 CE数量关系,并说明理由.
参考答案
一、1. D
2. D 【点拨】∵在矩形ABCD中,对角线 AC,BD 相交于点O,∴
3. D 【点拨】∵四边形ABCD是菱形,
在 中,根据勾股定 理, 得 ∴ BD=20B=8.
4. D 【点拨】∵ 四边形ABCD 是正方形,AC 是对角线
∵四边形 AEFC 是菱形,AF是对角线,
5. B 【点拨】∵DE 为△ABC 的中位线,BC=8,∴DE= 点D 是AB 的中点.
∵∠AFB=90°,AB=5,
6. B
7. D 【点拨】因为: 所以四边形AEDF是平行四边形,故 A 正确;若∠BAC=90°,则是矩形,故B正确;若AD⊥BC且AB=AC,则是菱形,故C 正确;由AD平分∠BAC,易知AE=DE,所以 AEDF 是菱形,故 D 错误.
8. D 【点拨】设 EF 交 AC于点O,易得四边形 AEPF是平行四边形,
9. A 【点拨】如图①,连接AC,
∵四边形 ABCD 是菱形,∴AB =BC.
∵∠B =60°, 是等边三角形,∴AB=AC =1 cm.
如图②,连接AC,∵四边形ABCD 是正方形,∴ BC = AB=1 cm,
10. A 【点 拨】∵ 四边形ABCD是矩形,
11. C 【点拨】如图,连接AE,CG,CF,
∵四边形 DEFG 是 正方形, DE = DG.
∵四边形 ABCD 是正方形, ∠ADC = 90°,
∴∠ADE=
∴ 点A,E,F,C 在同一条直线上时,EF +CF+AE最小,即 最小.连接AC,的最小值为 AC 的长,
在 Rt△ABC中, 的最小值为 .
12. C 【点拨】∵ 四边形 ABCD 是矩形,∴ AB=CD, ∥AC,∠BMC=90°,∴∠DNA =90°=∠BMC.
在△DNA和△BMC中 ∴△DNA≌△BMC(AAS),∴DN= BM,∠ADE =∠CBF,故 ① 正确.
在△ADE和△CBF中, . △ADE≌△CBF(ASA),∴AE=FC,DE =BF.
∵ CF>CM,∴AE>CM,故③错误.
∵DE=BF,DN=BM,∴ DE-DN=BF-BM,即NE=MF.
又∵DE∥BF,∴四边形NEMF 是平行四边形,∴EM∥FN,故②正确.
∵AB= CD,AE =CF,∴BE=DF.又∵ DE =BF,∴ 四边形 DEBF 是平行四边形.
∵ AO =AD,OA =OD,∴AO= AD=OD,∴△AOD是等边三角形,∴∠ADO=∠DAN=
AD= OD,∴∠ADN=∠ODN= 30°,
∴ ∠ODN =∠ABD,∴DE= BE,∴□DEBF是菱形,故④正确.
故正确结论的个数是3.
二、13.4 【点拨】∵ 菱形 ABCD 的周长为 32,∴ 菱形ABCD的边长为8,即AD=8.
∵ 四边形ABCD为菱形, ∴O为AC 的中点.
∵E为 CD的中点,∴
14. AB⊥BC(答案不唯一) 【点拨】∵D,E,F分别是AB,BC 和 AC 边的中点,
∴DF,EF 都是△ABC 的中位线,∴DF∥BC,EF∥AB,∴四边形BEFD为平行四边形.
当AB⊥BC时,∠B=90°,∴平行四边形BEFD为矩形.
15.(-4,3) 【点拨】如图,过点A 作AB⊥x轴于点B, 过点 D 作 DE⊥x轴于点E,则∠OAB+∠AOB =90°.
∵四边形 OACD 是正方形,∴OA=OD,∠AOD=90°,∴∠DOE+∠AOB=90°,∴∠OAB=∠DOE.
在△AOB和△ODE中, ∴△AOB≌△ODE(AAS),
∴ AB = OE,OB = DE.
∵点D的坐标为(3,4),∴OE=3,DE =4.∵ 点 A在第二象限,∴ 点A 的坐标为(-4,3).
【点拨】连接 OE,
∵ 四边形 ABCD 是矩形,∴∠ABC=90°,BC=AD=12,AO =CO=BO =DO.
.
17.20 【点拨】由题可知 MN 是线段 AD 的垂直平分线,∴AF =FD,AE =ED,AD⊥EF.
∵ AD 是△ABC的角平分线, ∴ ∠EAD=∠FAD,∴ ∠AFE =∠AEF,∴AF=AE,
∴ AF =FD=AE=ED,∴ 四边形AEDF 是菱形.
∵△CDF 的周长 =CD+DF+CF=CD+AF+CF=AC +CD=12,AC=8,∴CD=4.
设AF=FD=x,则CF=8-x.
∵在Rt△CDF 中, 解得 x =5,
18.(1)3
【点拨】(1)如图,过 E 作 ⊥AD于 M,
的面积为
(2)如图,延长EM 交 AG于N,交BC于P,
∵四边形ABCD是 E正方形,∴ AB∥CD,∠BAD=∠ABC = 90°.
∵ EM⊥AD,∴四边形 ABPM 是矩形, ∴ PM=AB =3,AB∥EP,
∴ PM∥CD,EP=5,∠ABF=∠NEF.
∵F 为BE的中点,∴BF=EF.
在△ABF和△NEF中,∴△ABF≌△NEF(ASA),
∴ EN=AB =3,∴ MN=1.
由PM∥CD,易知AN=
三、19.【证明】∵ 四边形ABCD 是菱形,∴ AB =BC=DC = AD,∠B= ∠D.
∵ CE ⊥AB,CF ⊥ AD, ∴∠CEB=∠CFD = 90°.
在△BCE 和△DCF 中, ∴ △BCE ≌ △DCF (AAS),
∴BE=DF,∴AB-BE=AD-DF,即AE=AF.
20.【证明】(1)∵ 四边形ABCD 是矩形,∴ AD∥BC, ∴∠EDO=∠FBO.
∵点O 是 BD的中点,∴DO=BO.
又∵∠EOD=∠FOB,∴△BOF≌△DOE(ASA).
(2)由(1)知△BOF≌△DOE,∴BF=DE.
∵ AD∥BC,即DE∥BF,∴ 四边形 EBFD 是平行四边形.
∵EF⊥BD,∴四边形EBFD 是菱形.
21.【证明】∵ DE∥AC, CE∥AD,∴四边形ADEC 是平行四边形. 又∵ ∴BC = DE.∵D为AB 的中点,∴
又∵CE∥DB,∴四边形CDBE 是平行四边形.
又∵BC=DE.∴ 四边形CDBE 是矩形.
D为AB的中点, 四边形 CDBE 是正方形.
22.【证明】(1)∵点 D,E 分别是 AB,BC 的中点,∴DE∥AC.同理可得∥∴ 四边形 ADEF 是平行四边形.
(2) 由(1) 知 四边 形 ADEF 是平行 四边 形,∴∠DAF=∠DEF.
在 中,∵D 是AB 的中点,.
同理可得
23.(1)【证明】∵ DE 是 的中位线,∴点 D 是AB 的中点,点 E 是 AC 的中点,
是△ABC的中线,∴点 F 是 BC 的中点,∴ EF 是△ABC的中位线,
∥AD,∴四边形ADFE 是平行四边形,
∴ AF 与DE 互相平分.
(2)【解】当 时,四边形 ADFE 为矩形.
理由:∵线段DE 为△ABC的中位线,
由(1)得四边形ADFE 是平行四边形,∴ 四边形ADFE 为矩形.
24.(1)【证明】∵ MN 是 AC的垂直平分线,∴AO=CO.
∵四边形ABCD 是矩形,∴AB∥CD,∴∠M=∠N.
在△AOM和△CON中 ∴△AOM≌△CON(AAS).
(2)【解】如图,连接 CE, ∵ MN是 AC 的垂直平分线,∴CE=AE,
设AE=CE=x,则DE=6-x.
∵ 四边形 ABCD 是矩形,∴ ∠CDE =90°,CD=AB =3.
在 Rt△CDE 中, 由勾股定理得
即解得 即AE 的长为
(1)【证明】在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°.
在△ABP和△CBP中,
∴ PA=PC.∵PA=PE,∴PC=PE.
(2)【解】由(1)知△ABP≌△CBP,∴ ∠BAP =∠BCP.
∵∠BAD=∠BCD=90°,∴∠DAP=∠DCP.
∵PA = PE,∴ ∠DAP = ∠E,∴ ∠DCP = ∠E.
∵∠CFP=∠EFD,∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,即∠CPE=∠EDF=90°.
(3)【解】AP = CE. 理由如下:
在菱形 ABCD 中,AB =BC,∠ABP=∠CBP,∠BAD=∠BCD,∠ADC=∠ABC = 120°.
在 △ABP 和 △CBP 中,
∴PA=PC,∠BAP =∠BCP,∴∠DAP =∠DCP.
∵PA=PE,∴PC=PE,∠DAP=∠AEP,∴∠DCP=∠AEP.
∵ ∠CFP = ∠EFD,∴180°-∠PFC -∠PCF = 180°-∠DFE - ∠AEP, 即∠CPF =∠EDF = 180°- ∠ADC = 180°-120°= 60°,∴△EPC是等边三角形,∴PC=CE,∴AP=CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 特殊平行四边形
单元检测题
(时间:90分钟 满分:120分)
一、选择题(每题3分,共36分)
1.菱形、矩形、正方形都具有的性质是( )
A.四条边相等,四个角相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
2.在矩形ABCD中,对角线AC,BD相交于点O,若AC=16, 则OD等于( )
A.16 B.12 C.10 D.8
3.如图,菱形ABCD的对角线 AC 与BD相交于点O,若AB=5,AC=6,则BD 的长为( )
A.4 B.6 C.7 D.8
(第3 题) (第4 题)
4.如图,以正方形 ABCD 的对角线AC为一边作菱形AEFC,则∠FAB的度数是( )
A.20° B.30° C.50° D.22.5°
5.如图,DE 为△ABC 的中位线,点 F 在 DE 上,且∠AFB=90°,若AB =5,BC=8,则EF的长为( )
A.2 B.1.5 C.2.5 D.3
6.在四边形ABCD中,∠A=∠B=∠C=90°.如果再添加一个条件可推出四边形ABCD 是正方形,那么这个条件可以是( )
A. AB=CD B. BC=CD C.∠D=90° D. AC=BD
7.如图,在△ABC中,点D在BC上, DE∥AC,DF∥AB,下列四个判断中不正确的是( )
A.四边形AEDF 是平行四边形
B.若 则四边形AEDF 是矩形
C.若 且 则四边形 AEDF 是菱形
D.若AD平分 则四边形 AEDF 是矩形
(第7题) (第8题)
8.如图,菱形ABCD的对角线的长分别为2 和5,P 是对角线AC 上任意一点(点P不与点A,C重合),且∥交AB 于点E, ∥交AD于点 F,则阴影部分的面积是( )
A.10 B.7.5 C.5 D.2.5
9.立德树人热爱劳动意识如图,小明用四根长度相同的木条制作能够活动的菱形学具,他先把活动学具做成图①所示的菱形,并测得 点A,C之间的距离是 1 cm,接着把活动学具做成图②所示的正方形,则图②中点A,C 之间的距离为( )
B.2 cm C.3 cm D.4 cm
(第9题) (第10题)
10.如图,在矩形ABCD中,对角线AC与BD 相交于点O,AE⊥BD于点E,∠DAE=2∠BAE,AB=2,则OE的长为( )
A.1 B. C.2
11.如图,正方形ABCD 的边长为2,E 为与点D 不重合的动点,以DE 为一边作正方形DEFG.设 点F,G与点C的距离分别为则 的最小值为( )
B.2 D.4
(第11 题) (第 12 题)
12.如图,在矩形ABCD 中,AC,BD 相交于点O,过点B作BF⊥AC交 CD于点 F,交AC 于点M,过点 D作 DE∥BF 交 AB 于点 E,交 AC 于点 N,连接FN,EM.则下列结论:①DN= BM;②EM∥FN;③AE=CM;④当AO=AD时,四边形DEBF 是菱形.其中,正确结论的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题3分,共18分)
13.如图,在菱形ABCD 中,E为 CD的中点,菱形ABCD的周长为32,则
(第13 题) (第14 题)
14.如图,在 中,D,E,F 分别是AB, BC 和AC边的中点,请添加一个条件:_________,使四边形BEFD为矩形.
15.如图,将正方形OACD 放在平面直角坐标系中,O 是坐标原点,点D的坐标为(3,4),则点A 的坐标为__________.
(第 15 题) (第 16题)
16.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD 中,对角线AC与BD 交于点O,点E 为BC 边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点 F,G,则EF +EG=____________.
17.如图,在△ABC 中, AD 是 的角平分线,分别以点A,D为圆心,大于 的长为半径作弧,两弧交于点 M,N,作直线 MN,分别交 AB,AC 于点E,F,连接DE,DF,若△CDF 的周长为 12,AC =8,则四边形AEDF 的面积为____________.
18.如图,在边长为3 的正方形ABCD 的外侧, 作等腰三角形ADE,
的面积为_________.
(2)若 F 为 BE 的中点,连接 AF 并延长,与 CD 相交于点 G,则AG 的长为________.
三、解答题(19~21 题每题8分,22~24 题每题10 分,25题12分,共66分)
19.如图,在菱形 ABCD 中,于点 E, 于点 F,求证:
20.如图,矩形 ABCD中,过对角线 BD的中点O 作BD的垂线EF,分别交 AD,BC 于点E,F.
(1)证明:
(2)连接 BE,DF,证明:四边形EBFD 是菱形.
21.如图,在 中, D 为 AB 的中点, ∥∥连接BE,CD.求证:四边形 CDBE是正方形.
22.如图,在 中,点D,E,F分别是AB,BC,CA 的中点, AH 是边 BC 上的高. 求证:
(1)四边形 ADEF 是平行四边形.
23.如图,线段DE 与AF 分别为 的中位线与中线.
(1)求证:AF 与DE 互相平分.
(2)当线段 AF 与BC 满足怎样的数量关系时,四边形 ADFE为矩形 请说明理由.
24.如图,在矩形ABCD中,对角线AC 的垂直平分线分别与边AB 和边 CD 的延长线交于点M,N,与边 AD交于点E,垂足为点 O.
(1)求证:
(2)若 求AE 的长.
25.如图①,在正方形ABCD 中,点P 是对角线 BD上的一点, 点 E 在 AD 的延长线上,且. PE 交 CD于点 F,
(1)证明:
(2)求 的度数.
(3)如图②,把正方形ABCD 改为菱形ABCD,其他条件不变,连接 CE,当时,试探究线段 AP 与线段 CE数量关系,并说明理由.
参考答案
一、1. D
2. D 【点拨】∵在矩形ABCD中,对角线 AC,BD 相交于点O,∴
3. D 【点拨】∵四边形ABCD是菱形,
在 中,根据勾股定 理, 得 ∴ BD=20B=8.
4. D 【点拨】∵ 四边形ABCD 是正方形,AC 是对角线
∵四边形 AEFC 是菱形,AF是对角线,
5. B 【点拨】∵DE 为△ABC 的中位线,BC=8,∴DE= 点D 是AB 的中点.
∵∠AFB=90°,AB=5,
6. B
7. D 【点拨】因为: 所以四边形AEDF是平行四边形,故 A 正确;若∠BAC=90°,则是矩形,故B正确;若AD⊥BC且AB=AC,则是菱形,故C 正确;由AD平分∠BAC,易知AE=DE,所以 AEDF 是菱形,故 D 错误.
8. D 【点拨】设 EF 交 AC于点O,易得四边形 AEPF是平行四边形,
9. A 【点拨】如图①,连接AC,
∵四边形 ABCD 是菱形,∴AB =BC.
∵∠B =60°, 是等边三角形,∴AB=AC =1 cm.
如图②,连接AC,∵四边形ABCD 是正方形,∴ BC = AB=1 cm,
10. A 【点 拨】∵ 四边形ABCD是矩形,
11. C 【点拨】如图,连接AE,CG,CF,
∵四边形 DEFG 是 正方形, DE = DG.
∵四边形 ABCD 是正方形, ∠ADC = 90°,
∴∠ADE=
∴ 点A,E,F,C 在同一条直线上时,EF +CF+AE最小,即 最小.连接AC,的最小值为 AC 的长,
在 Rt△ABC中, 的最小值为 .
12. C 【点拨】∵ 四边形 ABCD 是矩形,∴ AB=CD, ∥AC,∠BMC=90°,∴∠DNA =90°=∠BMC.
在△DNA和△BMC中 ∴△DNA≌△BMC(AAS),∴DN= BM,∠ADE =∠CBF,故 ① 正确.
在△ADE和△CBF中, . △ADE≌△CBF(ASA),∴AE=FC,DE =BF.
∵ CF>CM,∴AE>CM,故③错误.
∵DE=BF,DN=BM,∴ DE-DN=BF-BM,即NE=MF.
又∵DE∥BF,∴四边形NEMF 是平行四边形,∴EM∥FN,故②正确.
∵AB= CD,AE =CF,∴BE=DF.又∵ DE =BF,∴ 四边形 DEBF 是平行四边形.
∵ AO =AD,OA =OD,∴AO= AD=OD,∴△AOD是等边三角形,∴∠ADO=∠DAN=
AD= OD,∴∠ADN=∠ODN= 30°,
∴ ∠ODN =∠ABD,∴DE= BE,∴□DEBF是菱形,故④正确.
故正确结论的个数是3.
二、13.4 【点拨】∵ 菱形 ABCD 的周长为 32,∴ 菱形ABCD的边长为8,即AD=8.
∵ 四边形ABCD为菱形, ∴O为AC 的中点.
∵E为 CD的中点,∴
14. AB⊥BC(答案不唯一) 【点拨】∵D,E,F分别是AB,BC 和 AC 边的中点,
∴DF,EF 都是△ABC 的中位线,∴DF∥BC,EF∥AB,∴四边形BEFD为平行四边形.
当AB⊥BC时,∠B=90°,∴平行四边形BEFD为矩形.
15.(-4,3) 【点拨】如图,过点A 作AB⊥x轴于点B, 过点 D 作 DE⊥x轴于点E,则∠OAB+∠AOB =90°.
∵四边形 OACD 是正方形,∴OA=OD,∠AOD=90°,∴∠DOE+∠AOB=90°,∴∠OAB=∠DOE.
在△AOB和△ODE中, ∴△AOB≌△ODE(AAS),
∴ AB = OE,OB = DE.
∵点D的坐标为(3,4),∴OE=3,DE =4.∵ 点 A在第二象限,∴ 点A 的坐标为(-4,3).
【点拨】连接 OE,
∵ 四边形 ABCD 是矩形,∴∠ABC=90°,BC=AD=12,AO =CO=BO =DO.
.
17.20 【点拨】由题可知 MN 是线段 AD 的垂直平分线,∴AF =FD,AE =ED,AD⊥EF.
∵ AD 是△ABC的角平分线, ∴ ∠EAD=∠FAD,∴ ∠AFE =∠AEF,∴AF=AE,
∴ AF =FD=AE=ED,∴ 四边形AEDF 是菱形.
∵△CDF 的周长 =CD+DF+CF=CD+AF+CF=AC +CD=12,AC=8,∴CD=4.
设AF=FD=x,则CF=8-x.
∵在Rt△CDF 中, 解得 x =5,
18.(1)3
【点拨】(1)如图,过 E 作 ⊥AD于 M,
的面积为
(2)如图,延长EM 交 AG于N,交BC于P,
∵四边形ABCD是 E正方形,∴ AB∥CD,∠BAD=∠ABC = 90°.
∵ EM⊥AD,∴四边形 ABPM 是矩形, ∴ PM=AB =3,AB∥EP,
∴ PM∥CD,EP=5,∠ABF=∠NEF.
∵F 为BE的中点,∴BF=EF.
在△ABF和△NEF中,∴△ABF≌△NEF(ASA),
∴ EN=AB =3,∴ MN=1.
由PM∥CD,易知AN=
三、19.【证明】∵ 四边形ABCD 是菱形,∴ AB =BC=DC = AD,∠B= ∠D.
∵ CE ⊥AB,CF ⊥ AD, ∴∠CEB=∠CFD = 90°.
在△BCE 和△DCF 中, ∴ △BCE ≌ △DCF (AAS),
∴BE=DF,∴AB-BE=AD-DF,即AE=AF.
20.【证明】(1)∵ 四边形ABCD 是矩形,∴ AD∥BC, ∴∠EDO=∠FBO.
∵点O 是 BD的中点,∴DO=BO.
又∵∠EOD=∠FOB,∴△BOF≌△DOE(ASA).
(2)由(1)知△BOF≌△DOE,∴BF=DE.
∵ AD∥BC,即DE∥BF,∴ 四边形 EBFD 是平行四边形.
∵EF⊥BD,∴四边形EBFD 是菱形.
21.【证明】∵ DE∥AC, CE∥AD,∴四边形ADEC 是平行四边形. 又∵ ∴BC = DE.∵D为AB 的中点,∴
又∵CE∥DB,∴四边形CDBE 是平行四边形.
又∵BC=DE.∴ 四边形CDBE 是矩形.
D为AB的中点, 四边形 CDBE 是正方形.
22.【证明】(1)∵点 D,E 分别是 AB,BC 的中点,∴DE∥AC.同理可得∥∴ 四边形 ADEF 是平行四边形.
(2) 由(1) 知 四边 形 ADEF 是平行 四边 形,∴∠DAF=∠DEF.
在 中,∵D 是AB 的中点,.
同理可得
23.(1)【证明】∵ DE 是 的中位线,∴点 D 是AB 的中点,点 E 是 AC 的中点,
是△ABC的中线,∴点 F 是 BC 的中点,∴ EF 是△ABC的中位线,
∥AD,∴四边形ADFE 是平行四边形,
∴ AF 与DE 互相平分.
(2)【解】当 时,四边形 ADFE 为矩形.
理由:∵线段DE 为△ABC的中位线,
由(1)得四边形ADFE 是平行四边形,∴ 四边形ADFE 为矩形.
24.(1)【证明】∵ MN 是 AC的垂直平分线,∴AO=CO.
∵四边形ABCD 是矩形,∴AB∥CD,∴∠M=∠N.
在△AOM和△CON中 ∴△AOM≌△CON(AAS).
(2)【解】如图,连接 CE, ∵ MN是 AC 的垂直平分线,∴CE=AE,
设AE=CE=x,则DE=6-x.
∵ 四边形 ABCD 是矩形,∴ ∠CDE =90°,CD=AB =3.
在 Rt△CDE 中, 由勾股定理得
即解得 即AE 的长为
(1)【证明】在正方形ABCD中,AB=BC,∠ABP=∠CBP=45°.
在△ABP和△CBP中,
∴ PA=PC.∵PA=PE,∴PC=PE.
(2)【解】由(1)知△ABP≌△CBP,∴ ∠BAP =∠BCP.
∵∠BAD=∠BCD=90°,∴∠DAP=∠DCP.
∵PA = PE,∴ ∠DAP = ∠E,∴ ∠DCP = ∠E.
∵∠CFP=∠EFD,∴180°-∠PFC-∠PCF=180°-∠DFE-∠E,即∠CPE=∠EDF=90°.
(3)【解】AP = CE. 理由如下:
在菱形 ABCD 中,AB =BC,∠ABP=∠CBP,∠BAD=∠BCD,∠ADC=∠ABC = 120°.
在 △ABP 和 △CBP 中,
∴PA=PC,∠BAP =∠BCP,∴∠DAP =∠DCP.
∵PA=PE,∴PC=PE,∠DAP=∠AEP,∴∠DCP=∠AEP.
∵ ∠CFP = ∠EFD,∴180°-∠PFC -∠PCF = 180°-∠DFE - ∠AEP, 即∠CPF =∠EDF = 180°- ∠ADC = 180°-120°= 60°,∴△EPC是等边三角形,∴PC=CE,∴AP=CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
