2.2.3 运用乘法公式进行计算 课件(共24张PPT)
文档属性
| 名称 | 2.2.3 运用乘法公式进行计算 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:40 | ||
图片预览








文档简介
(共24张PPT)
2.2.3 运用乘法公式进行计算
1.熟练地运用乘法公式进行计算.
2.能正确地根据题目的要求选择不同的乘法公式进行运算.
3.提高学生对乘法公式综合运用的能力,分析、解决问题的能力.
4.培养学生实事求是、科学严谨的学习态度.
【教学重点】
正确选择乘法公式进行运算.
【教学难点】
综合运用平方差和完全平方公式进行多项式的计算.
请同学们回忆我们学过的平方差公式与完全平方公式:
注意:公式中的 a 与 b 既可以是数,也可以是单项式或多项式.
思考
(1)( x+1 )( x2+1 )( x-1 )=?
(2)(x+y+1)( x+y-1 )=
(1)(x+1)(x2+1)(x-1);
(2)(x+y+1)(x+y-1).
你能用简单的方法计算上面的式子吗?
(x+1)(x2+1)(x-1)
= (x+1)(x-1)(x2+1)
= (x2-1)(x2+1)
= x4-1
(交换律)
(1)(x+1)(x2+1)(x-1);
(2)(x+y+1)(x+y-1).
你能用简单的方法计算上面的式子吗?
把 x+y 看做一个整体
(x + y + 1)(x + y-1)
=[(x + y) + 1][(x + y)-1]
= (x + y)2-1
= x2 + 2xy + y2-1
遇到多项式的乘法时,我们要先观察式子的特征,看能否运用乘法公式,以达到简化运算的目的.
【例8】运用乘法公式计算:
(1)[(a+3)(a-3)]2;
解:(1)[(a+3)(a-3)]2
= (a2-9)2
= (a2)2-2·a2·9 + 92
= a4-18a2+81
(2)(a-b+c)(a+b-c).
平方差公式
完全平方公式:
(1)[(a+3)(a-3)]2;
(2)(a-b+c)(a+b-c).
(2)(a-b+c)(a+b-c)
= [a-(b-c)][a+(b-c)]
= a2-(b-c)2
= a2-(b2-2bc+c2)
= a2-b2+2bc-c2
平方差公式
完全平方公式:
【例8】运用乘法公式计算:
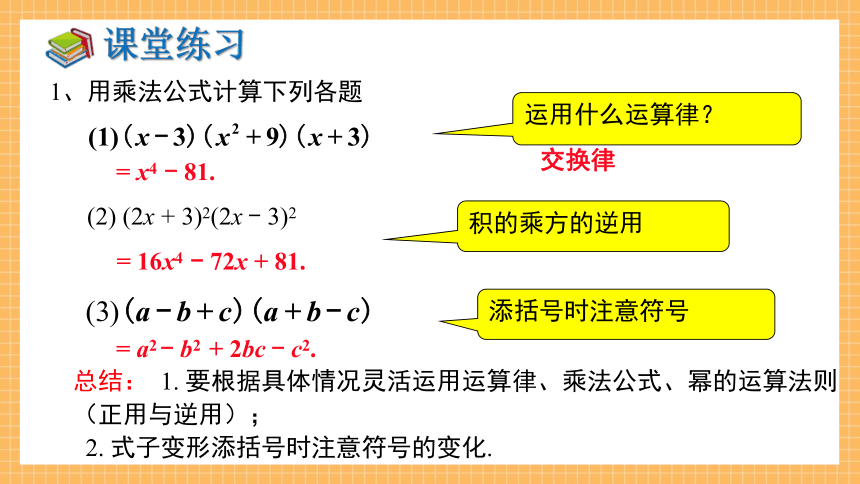
1、用乘法公式计算下列各题
= x4 - 81.
= 16x4 - 72x + 81.
= a2 - b2 + 2bc - c2.
添括号时注意符号
运用什么运算律?
积的乘方的逆用
(2) (2x + 3)2(2x - 3)2
总结: 1. 要根据具体情况灵活运用运算律、乘法公式、幂的运算法则(正用与逆用);
2. 式子变形添括号时注意符号的变化.
交换律
2、运用乘法公式计算:
( a + b + c )2 .
遇到多项式的乘法时,我们要先观察式子的特征,看能否运用乘法公式,以到达简化运算的目的.
解: ( a + b + c )2
= [(a + b) + c]2
= (a + b)2 + 2c(a + b) + c2
= a2 + 2ab + b2 + 2ac + 2bc + c2
= a2 + b2 + c2 + 2ab + 2ac + 2bc
课本P49例题:一个正方形花圃的边长增加到原来2倍还多1m,它的面积就增加到原来的4倍还多21m2 ,求这个正方形花圃原来的边长.
解 :设正方形花圃原来的边长为 x m.
由数量关系 得:(2x +1)2= 4x 2+21
化简得: 4x 2+4x +1= 4x 2 +21
即 4x = 20
解得 x = 5.
答: 这个正方形花圃原来的边长为 5 m.
3、运用乘法公式计算:(x + 2y – 3)(x – 2y + 3).
方法总结:选用平方差公式进行计算,需要分组.分组方法是“符号相同的为一组,符号相反的为另一组”.
解:原式= [ x + (2y – 3)][x – (2y – 3)]
= x2 – (2y – 3)2
= x2 – (4y2 – 12y + 9)
= x2 – 4y2 + 12y – 9.
4、计算:(1)(a-b+c)2;
(2)(1-2x+y)(1+2x-y).
=1-4x2+4xy-y2.
解:(1)原式=[(a-b)+c]2
=(a-b)2+c2+2(a-b)c
=a2-2ab+b2+c2+2ac-2bc.
(2)原式=[1+(-2x+y)][1-(-2x+y)]
=12-(-2x+y)2
1.下列运算中,正确的是( )
A. (a+3)(a-3) = a2-3
B. (3b+2)(3b-2) = 3b2-4
C. (3m-2n)(-2n-3m) = 4n2-9m2
D. (x+2)(x-3) = x2-6
C
2.运用乘法公式计算:
(1)( x-2 )( x+2 )( x2+4 ); (2)( a+2b-1 )( a+2b+1 );
(3)( 2m+n-1 )( 2m-n+1 ); (4)( x+1 )2( x-1 )2.
答案:(1)x4-16; (2)a2+4ab+4b2-1;
(3)4m2-n2+2n-1; (4)x4-2x2+1.
(1)(x - 2)(x + 2)(x2 + 4)
(2)(x - 1)2 - (x + 1)2
(3)(x + 1)2(x - 1)2
(4)(a + 2b - 1)(a + 2b + 1)
(5)(a - b - c) 2
3.运用乘法公式计算 :
= x4 - 16
= -4x
= x4 - 2x2 + 1
= a2 + 4ab + 4b2 - 1
= a2 + b2 + c2 - 2ab - 2ac + 2bc
4. 解方程:
5x + 6(3x + 2)(-2 + 3x) - 54 (x- )(x+ ) = 2
解: 5x + 6(9x2 - 4 ) – 54 (x2- ) = 2
5x+54x2-24-54x2+6 = 2
5x = 20
x = 4
5.一个正方形的边长增加了 2 cm,它的面积就增加了 16 cm2,求这个正方形原来的边长.
答:这个正方形原来的边长为 3 cm.
解:设正方形原来的边长为 x cm.
列方程,得 (x + 2)2 = x2 + 16,
解得 x = 3.
x2 + 4x + 4 = x2 + 16,
4x = 12,
6. 计算:
(a-b-c)2
解:(a-b-c)2
= [a - (b + c)]2
= a2 - 2a(b + c) + (b + c)2
= a2 - 2ab - 2ac + b2 + 2bc + c2
= a2 + b2 + c2 - 2ab - 2ac + 2bc.
7.先化简,再求值:
2b2 + (a + b)(a - b) - (a - b)2,其中 a = -3,b = .
解:原式 = 2b2 + a2 - b2 - a2 + 2ab - b2 = 2ab.
当 a = - 3,b = 时,
原式 = 2×(-3)× = -3.
(1) 平方差公式:
(a+b)2 =
(a+b)(a-b) =
(2)完全平方公式:
a -2ab+b
a +2ab+b
(a-b) =
a -b
注意: 公式中的 a 与 b 既可以是数,又可以是单项式 和 多项式.
如何运用乘法公式进行计算:
3. 灵活运用公式进行求值计算.
2. 有时会结合其它运算法则;
1. 先观察式子的特点,选取适当的乘法公式;
1.习题“2.2”中第5、6题.
2.完成同步练习册中本课时的练习.
2.2.3 运用乘法公式进行计算
1.熟练地运用乘法公式进行计算.
2.能正确地根据题目的要求选择不同的乘法公式进行运算.
3.提高学生对乘法公式综合运用的能力,分析、解决问题的能力.
4.培养学生实事求是、科学严谨的学习态度.
【教学重点】
正确选择乘法公式进行运算.
【教学难点】
综合运用平方差和完全平方公式进行多项式的计算.
请同学们回忆我们学过的平方差公式与完全平方公式:
注意:公式中的 a 与 b 既可以是数,也可以是单项式或多项式.
思考
(1)( x+1 )( x2+1 )( x-1 )=?
(2)(x+y+1)( x+y-1 )=
(1)(x+1)(x2+1)(x-1);
(2)(x+y+1)(x+y-1).
你能用简单的方法计算上面的式子吗?
(x+1)(x2+1)(x-1)
= (x+1)(x-1)(x2+1)
= (x2-1)(x2+1)
= x4-1
(交换律)
(1)(x+1)(x2+1)(x-1);
(2)(x+y+1)(x+y-1).
你能用简单的方法计算上面的式子吗?
把 x+y 看做一个整体
(x + y + 1)(x + y-1)
=[(x + y) + 1][(x + y)-1]
= (x + y)2-1
= x2 + 2xy + y2-1
遇到多项式的乘法时,我们要先观察式子的特征,看能否运用乘法公式,以达到简化运算的目的.
【例8】运用乘法公式计算:
(1)[(a+3)(a-3)]2;
解:(1)[(a+3)(a-3)]2
= (a2-9)2
= (a2)2-2·a2·9 + 92
= a4-18a2+81
(2)(a-b+c)(a+b-c).
平方差公式
完全平方公式:
(1)[(a+3)(a-3)]2;
(2)(a-b+c)(a+b-c).
(2)(a-b+c)(a+b-c)
= [a-(b-c)][a+(b-c)]
= a2-(b-c)2
= a2-(b2-2bc+c2)
= a2-b2+2bc-c2
平方差公式
完全平方公式:
【例8】运用乘法公式计算:
1、用乘法公式计算下列各题
= x4 - 81.
= 16x4 - 72x + 81.
= a2 - b2 + 2bc - c2.
添括号时注意符号
运用什么运算律?
积的乘方的逆用
(2) (2x + 3)2(2x - 3)2
总结: 1. 要根据具体情况灵活运用运算律、乘法公式、幂的运算法则(正用与逆用);
2. 式子变形添括号时注意符号的变化.
交换律
2、运用乘法公式计算:
( a + b + c )2 .
遇到多项式的乘法时,我们要先观察式子的特征,看能否运用乘法公式,以到达简化运算的目的.
解: ( a + b + c )2
= [(a + b) + c]2
= (a + b)2 + 2c(a + b) + c2
= a2 + 2ab + b2 + 2ac + 2bc + c2
= a2 + b2 + c2 + 2ab + 2ac + 2bc
课本P49例题:一个正方形花圃的边长增加到原来2倍还多1m,它的面积就增加到原来的4倍还多21m2 ,求这个正方形花圃原来的边长.
解 :设正方形花圃原来的边长为 x m.
由数量关系 得:(2x +1)2= 4x 2+21
化简得: 4x 2+4x +1= 4x 2 +21
即 4x = 20
解得 x = 5.
答: 这个正方形花圃原来的边长为 5 m.
3、运用乘法公式计算:(x + 2y – 3)(x – 2y + 3).
方法总结:选用平方差公式进行计算,需要分组.分组方法是“符号相同的为一组,符号相反的为另一组”.
解:原式= [ x + (2y – 3)][x – (2y – 3)]
= x2 – (2y – 3)2
= x2 – (4y2 – 12y + 9)
= x2 – 4y2 + 12y – 9.
4、计算:(1)(a-b+c)2;
(2)(1-2x+y)(1+2x-y).
=1-4x2+4xy-y2.
解:(1)原式=[(a-b)+c]2
=(a-b)2+c2+2(a-b)c
=a2-2ab+b2+c2+2ac-2bc.
(2)原式=[1+(-2x+y)][1-(-2x+y)]
=12-(-2x+y)2
1.下列运算中,正确的是( )
A. (a+3)(a-3) = a2-3
B. (3b+2)(3b-2) = 3b2-4
C. (3m-2n)(-2n-3m) = 4n2-9m2
D. (x+2)(x-3) = x2-6
C
2.运用乘法公式计算:
(1)( x-2 )( x+2 )( x2+4 ); (2)( a+2b-1 )( a+2b+1 );
(3)( 2m+n-1 )( 2m-n+1 ); (4)( x+1 )2( x-1 )2.
答案:(1)x4-16; (2)a2+4ab+4b2-1;
(3)4m2-n2+2n-1; (4)x4-2x2+1.
(1)(x - 2)(x + 2)(x2 + 4)
(2)(x - 1)2 - (x + 1)2
(3)(x + 1)2(x - 1)2
(4)(a + 2b - 1)(a + 2b + 1)
(5)(a - b - c) 2
3.运用乘法公式计算 :
= x4 - 16
= -4x
= x4 - 2x2 + 1
= a2 + 4ab + 4b2 - 1
= a2 + b2 + c2 - 2ab - 2ac + 2bc
4. 解方程:
5x + 6(3x + 2)(-2 + 3x) - 54 (x- )(x+ ) = 2
解: 5x + 6(9x2 - 4 ) – 54 (x2- ) = 2
5x+54x2-24-54x2+6 = 2
5x = 20
x = 4
5.一个正方形的边长增加了 2 cm,它的面积就增加了 16 cm2,求这个正方形原来的边长.
答:这个正方形原来的边长为 3 cm.
解:设正方形原来的边长为 x cm.
列方程,得 (x + 2)2 = x2 + 16,
解得 x = 3.
x2 + 4x + 4 = x2 + 16,
4x = 12,
6. 计算:
(a-b-c)2
解:(a-b-c)2
= [a - (b + c)]2
= a2 - 2a(b + c) + (b + c)2
= a2 - 2ab - 2ac + b2 + 2bc + c2
= a2 + b2 + c2 - 2ab - 2ac + 2bc.
7.先化简,再求值:
2b2 + (a + b)(a - b) - (a - b)2,其中 a = -3,b = .
解:原式 = 2b2 + a2 - b2 - a2 + 2ab - b2 = 2ab.
当 a = - 3,b = 时,
原式 = 2×(-3)× = -3.
(1) 平方差公式:
(a+b)2 =
(a+b)(a-b) =
(2)完全平方公式:
a -2ab+b
a +2ab+b
(a-b) =
a -b
注意: 公式中的 a 与 b 既可以是数,又可以是单项式 和 多项式.
如何运用乘法公式进行计算:
3. 灵活运用公式进行求值计算.
2. 有时会结合其它运算法则;
1. 先观察式子的特点,选取适当的乘法公式;
1.习题“2.2”中第5、6题.
2.完成同步练习册中本课时的练习.
