河北省保定市高阳中学2014-2015学年高一下学期第十二次周练数学试题
文档属性
| 名称 | 河北省保定市高阳中学2014-2015学年高一下学期第十二次周练数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 149.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-24 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
高一数学周练七十一
1.正方体的表面积是96,则正方体的体积为( )
A.48 B.16
C.64 D.96
2.直径为10 cm的一个大金属球,熔化后铸成若干个直径为2 cm的小球,如果不计损耗,可铸成这样的小球的个数为( )21世纪教育网版权所有
A.5 B.15
C.25 D.125
3.将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括( )
A.一个圆台,两个圆锥 B.两个圆台,一个圆锥
C.两个圆台,一个圆柱 D.一个圆柱,两个圆锥
4.一个几何体的三视图如图所示,则该几何体的直观图可以是( )
5.如图,梯形A1B1C1D1是一平面图 ( http: / / www.21cnjy.com )形ABCD的直观图(斜二测),若A1D1∥O1y1,A1B1∥C1D1,A1B1=C1D1=2,A1D1=1,则梯形ABCD的面积是( )21教育网
A.10 B.5
C.5 D.10
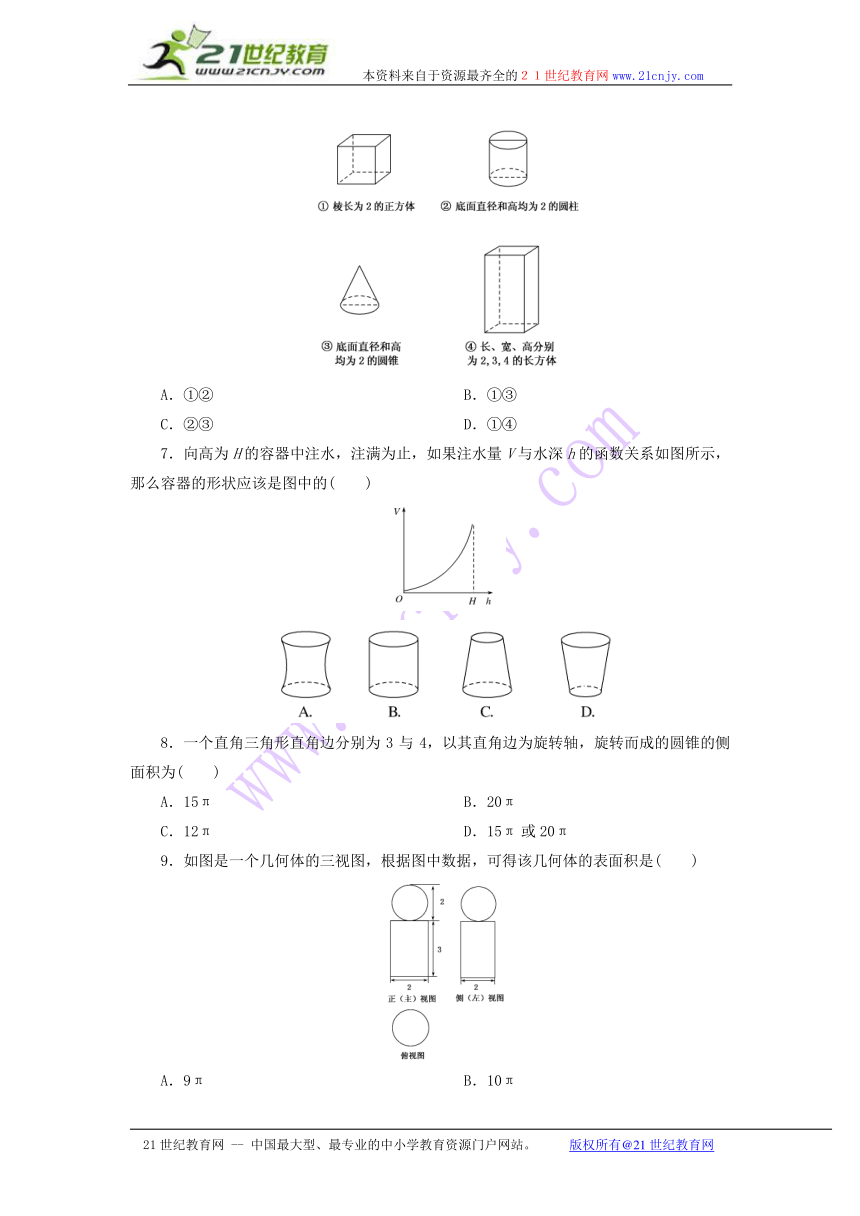
6.如图,下列四个几何体中,它们的三视图(正视图、侧视图、俯视图)有且仅有两个相同的是( )
A.①② B.①③
C.②③ D.①④
7.向高为H的容器中注水,注满为止,如果注水量V与水深h的函数关系如图所示,那么容器的形状应该是图中的( )21·cn·jy·com
8.一个直角三角形直角边分别为3与4,以其直角边为旋转轴,旋转而成的圆锥的侧面积为( )
A.15π B.20π
C.12π D.15π或20π
9.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
A.9π B.10π
C.11π D.12π
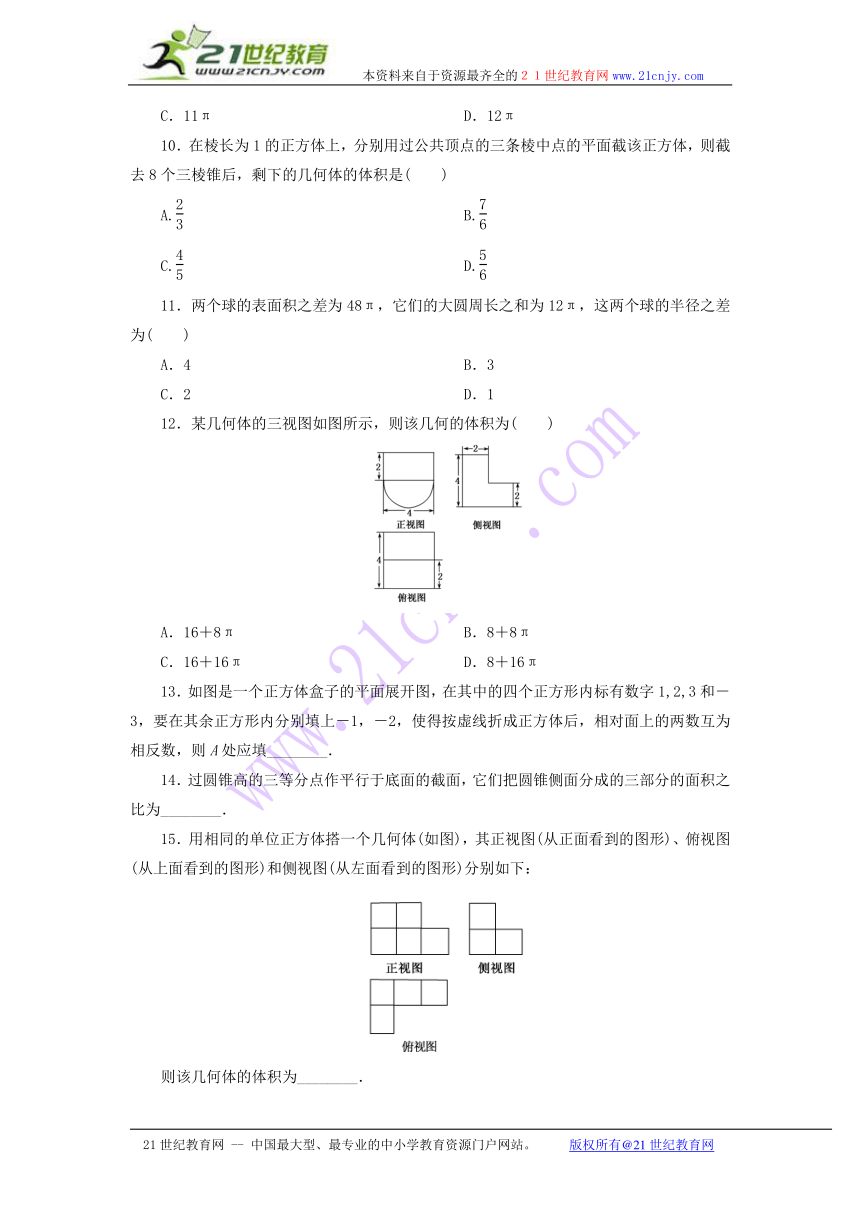
10.在棱长为1的正方体上,分别用过公共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是( )www.21-cn-jy.com
A. B.
C. D.
11.两个球的表面积之差为48π,它们的大圆周长之和为12π,这两个球的半径之差为( )
A.4 B.3
C.2 D.1
12.某几何体的三视图如图所示,则该几何的体积为( )
A.16+8π B.8+8π
C.16+16π D.8+16π
13.如图是一个正方体盒子的平面展开图,在其中的四个正方形内标有数字1,2,3和-3,要在其余正方形内分别填上-1,-2,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填________.21cnjy.com
14.过圆锥高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为________.21世纪教育网2·1·c·n·j·y
15.用相同的单位正方体搭一个几何体(如图),其正视图(从正面看到的图形)、俯视图(从上面看到的图形)和侧视图(从左面看到的图形)分别如下:【来源:21·世纪·教育·网】
则该几何体的体积为________.
16.已知一个圆台的下底面半径为r,高为h,当圆台的上底半径r′变化时,圆台体积的变化范围是________.21·世纪*教育网
17.(10分)如图所示,在边长为4的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC, EH⊥BC,FG⊥BC,D,H,G为垂足,若将△ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.www-2-1-cnjy-com
18.(12分)一个正三棱柱的三视图如图所示,求这个正三棱柱的表面积.
21世纪教育网
19.(12分)已知圆台的上底面半径为r,下底面半径为R,母线长为l,试证明圆台的侧面积公式为:S圆台侧面积=π (r+R)l,表面积公式为S=π (R2+r2+Rl+rl).
20.(12分)侧棱垂直底面的棱柱叫直棱柱.已知底面是菱形的直棱柱,它的体对角线分别为9和15,高是5,求这个棱柱的侧面积.2-1-c-n-j-y
21.(12分)如图,BD是正方形ABCD的对角线,的圆心是A,半径为AB,正方形ABCD以AB为轴旋转一周,求图中Ⅰ、Ⅱ、Ⅲ三部分旋转所得旋转体的体积之比.
22.(12分)一几何体按比例绘制的三视图如图所示(单位:m).
(1)试画出它的直观图;
(2)求它的表面积和体积.
21世纪教育网
答案:
1.C
2. D
3.D
4.D
5. B
6.C
7.D
8. D
9. D
10. D
11.C
12. A
13. -2
14. 1:3:5
15. 6
16.
17. 2(6+)π.
18. 8(3+)(mm)2.
19.证明 把圆台还原成圆锥,并作出轴截面,如图:21世纪教育网
设AB=x,BC=l,∵△ABF∽△ACG.
∴=,∴x=.
∴S圆台侧=S扇形ACD-S扇形ABE
=·2πR(x+l)-·2πr·x[21世纪教育网]
=πRl+π(R-r)·
=π (R+r)l
∴S圆台表面积=π(R+r)l+πR2+πr2
=π(Rl+rl+R2+r2).
20.160.
21. 1:1:1.
22. (1)直观图如图所示.
(2)表面积为(7+) m2,体积为 m3.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
高一数学周练七十一
1.正方体的表面积是96,则正方体的体积为( )
A.48 B.16
C.64 D.96
2.直径为10 cm的一个大金属球,熔化后铸成若干个直径为2 cm的小球,如果不计损耗,可铸成这样的小球的个数为( )21世纪教育网版权所有
A.5 B.15
C.25 D.125
3.将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括( )
A.一个圆台,两个圆锥 B.两个圆台,一个圆锥
C.两个圆台,一个圆柱 D.一个圆柱,两个圆锥
4.一个几何体的三视图如图所示,则该几何体的直观图可以是( )
5.如图,梯形A1B1C1D1是一平面图 ( http: / / www.21cnjy.com )形ABCD的直观图(斜二测),若A1D1∥O1y1,A1B1∥C1D1,A1B1=C1D1=2,A1D1=1,则梯形ABCD的面积是( )21教育网
A.10 B.5
C.5 D.10
6.如图,下列四个几何体中,它们的三视图(正视图、侧视图、俯视图)有且仅有两个相同的是( )
A.①② B.①③
C.②③ D.①④
7.向高为H的容器中注水,注满为止,如果注水量V与水深h的函数关系如图所示,那么容器的形状应该是图中的( )21·cn·jy·com
8.一个直角三角形直角边分别为3与4,以其直角边为旋转轴,旋转而成的圆锥的侧面积为( )
A.15π B.20π
C.12π D.15π或20π
9.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
A.9π B.10π
C.11π D.12π
10.在棱长为1的正方体上,分别用过公共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是( )www.21-cn-jy.com
A. B.
C. D.
11.两个球的表面积之差为48π,它们的大圆周长之和为12π,这两个球的半径之差为( )
A.4 B.3
C.2 D.1
12.某几何体的三视图如图所示,则该几何的体积为( )
A.16+8π B.8+8π
C.16+16π D.8+16π
13.如图是一个正方体盒子的平面展开图,在其中的四个正方形内标有数字1,2,3和-3,要在其余正方形内分别填上-1,-2,使得按虚线折成正方体后,相对面上的两数互为相反数,则A处应填________.21cnjy.com
14.过圆锥高的三等分点作平行于底面的截面,它们把圆锥侧面分成的三部分的面积之比为________.21世纪教育网2·1·c·n·j·y
15.用相同的单位正方体搭一个几何体(如图),其正视图(从正面看到的图形)、俯视图(从上面看到的图形)和侧视图(从左面看到的图形)分别如下:【来源:21·世纪·教育·网】
则该几何体的体积为________.
16.已知一个圆台的下底面半径为r,高为h,当圆台的上底半径r′变化时,圆台体积的变化范围是________.21·世纪*教育网
17.(10分)如图所示,在边长为4的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC, EH⊥BC,FG⊥BC,D,H,G为垂足,若将△ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.www-2-1-cnjy-com
18.(12分)一个正三棱柱的三视图如图所示,求这个正三棱柱的表面积.
21世纪教育网
19.(12分)已知圆台的上底面半径为r,下底面半径为R,母线长为l,试证明圆台的侧面积公式为:S圆台侧面积=π (r+R)l,表面积公式为S=π (R2+r2+Rl+rl).
20.(12分)侧棱垂直底面的棱柱叫直棱柱.已知底面是菱形的直棱柱,它的体对角线分别为9和15,高是5,求这个棱柱的侧面积.2-1-c-n-j-y
21.(12分)如图,BD是正方形ABCD的对角线,的圆心是A,半径为AB,正方形ABCD以AB为轴旋转一周,求图中Ⅰ、Ⅱ、Ⅲ三部分旋转所得旋转体的体积之比.
22.(12分)一几何体按比例绘制的三视图如图所示(单位:m).
(1)试画出它的直观图;
(2)求它的表面积和体积.
21世纪教育网
答案:
1.C
2. D
3.D
4.D
5. B
6.C
7.D
8. D
9. D
10. D
11.C
12. A
13. -2
14. 1:3:5
15. 6
16.
17. 2(6+)π.
18. 8(3+)(mm)2.
19.证明 把圆台还原成圆锥,并作出轴截面,如图:21世纪教育网
设AB=x,BC=l,∵△ABF∽△ACG.
∴=,∴x=.
∴S圆台侧=S扇形ACD-S扇形ABE
=·2πR(x+l)-·2πr·x[21世纪教育网]
=πRl+π(R-r)·
=π (R+r)l
∴S圆台表面积=π(R+r)l+πR2+πr2
=π(Rl+rl+R2+r2).
20.160.
21. 1:1:1.
22. (1)直观图如图所示.
(2)表面积为(7+) m2,体积为 m3.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
