五年级下册数学人教版3.5 长方体和正方体练习十 课件(19张ppt)
文档属性
| 名称 | 五年级下册数学人教版3.5 长方体和正方体练习十 课件(19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 20:22:08 | ||
图片预览


文档简介
(共19张PPT)
练习十
第三单元 长方体和正方体
长方体和正方体的认识
6个面
12条棱
8个顶点
正方体是特殊的长方体
长方体和正方体的表面积
长方体或正方体6个面的总面积,叫作它的表面积。
长方体表面积=(长×宽+长×高+宽×高)×2
正方体表面积=棱长×棱长×6
长方体和正方体的体积
物体所占空间的大小叫作物体的体积。
长方体体积=长×宽×高
V=abh
正方体体积=棱长×棱长×棱长
a
b
h
a
a
a
V=a
体积单位间的进率
1立方分米=1000立方厘米
1立方米=1000立方分米
相邻的两个体积单位之间的进率是1000。
1dm =1000cm
1m =1000dm
计量容积,一般用体积单位;液体的体积,常用容积单位L和mL。
1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
容积和容积单位
1
选自教材第43页练习十
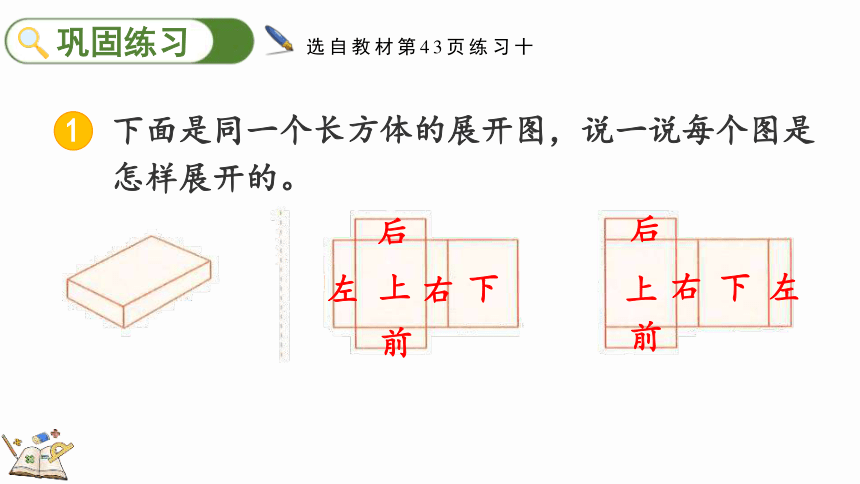
下面是同一个长方体的展开图,说一说每个图是怎样展开的。
上
左
右
前
后
下
上
右
前
后
下
左
找一些正方体纸盒将其展开,你能展开成多少种不同的形状?
“141”型
“231”型
“222”型
“33”型
2
长方体的长、宽、高都变为原来的 2 倍,它的表面积和体积分别发生了什么变化?你发现了什么规律?
长方体 长/cm 宽/cm 高/cm 表面积/cm2 体积/cm3
① 2 1 3
② 4 2 6
③ 8 4 12
22
6
88
48
352
384
规律:如果长方体的长、宽、高都变为原来的 2 倍,
它的表面积变为原来的 4 倍,体积变为原来的 8 倍。
3
一个长方体鱼塘长 8 m,宽 4.5 m,深 2 m。这个鱼塘的容积是多少?
8×4.5×2 = 72(m3)
答:这个鱼塘的容积是72立方米。
4
某古建筑景点定做了 25 个宫灯(如右图,单位:cm)。宫灯外侧有一层外饰面(上、下面除外)。如果外饰面每平方米18元,这些宫灯的外饰面一共要花多少钱?
18×50 = 900(元)
(66×20×4+46×80×4)×25
=(5280+14720)×25
= 500000(cm2)
= 50(m2)
答:这些宫灯的外饰面一共要花900元。
长方体有( )个面,( )个顶点,( )条棱,相对的两个面( )。一个长方体最多有( )个面完全相同。
6
8
12
完全相同
4
比较正方体有什么不同呢?
1.
一个长12厘米、宽8厘米、高5厘米的长方体,这个长方体六个面中最大面的面积是( )平方厘米,最小面的面积是( )平方厘米。
12厘米
8厘米
5厘米
长×宽
宽×高
96
40
2.
判断:
棱长是6分米的正方体的表面积和体积相等。
( )
体积和面积是两个不同的概念,两者单位不同,不能比较大小。
×
3.
一个菜窖能容纳6立方米白菜,说明这个菜窖的( )是6立方米。
A.体积 B.容积 C.表面积
B
所能容纳物体的体积,通常叫作它们的容积。
4.
(30×20+30×15+20×15)×2=2700(平方厘米)
答:需要2700平方厘米彩纸。
爸爸买了一个长30厘米、宽20厘米、高15厘米的长方体礼盒,里面装有妈妈爱吃的长方体形状的花生酥,每块花生酥长5厘米、宽3厘米、高2厘米。
(1)礼盒用彩纸包装,需要多少彩纸?(重叠部分不计算)
5.
长方体礼盒的表面积。
(30÷5)×(20÷2)×(15÷3)=300(块)
答:最多能装300块花生酥。
长方体的摆法不同,长、宽、高不同。
爸爸买了一个长30厘米、宽20厘米、高15厘米的长方体礼盒,里面装有妈妈爱吃的长方体形状的花生酥,每块花生酥长5厘米、宽3厘米、高2厘米。
(2)最多能装多少块花生酥?
5.
行数
列数
层数
× ×
这节课有什么收获呢?
在解决有关表面积的实际问题时,要根据具体情况确定要算哪几个面。
练习十
长方体表面积=(长×宽+长×高+宽×高)×2
正方体表面积=棱长×棱长×6
V=abh
V=a
V=Sh
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
1dm =1000cm
1m =1000dm
练习十
第三单元 长方体和正方体
长方体和正方体的认识
6个面
12条棱
8个顶点
正方体是特殊的长方体
长方体和正方体的表面积
长方体或正方体6个面的总面积,叫作它的表面积。
长方体表面积=(长×宽+长×高+宽×高)×2
正方体表面积=棱长×棱长×6
长方体和正方体的体积
物体所占空间的大小叫作物体的体积。
长方体体积=长×宽×高
V=abh
正方体体积=棱长×棱长×棱长
a
b
h
a
a
a
V=a
体积单位间的进率
1立方分米=1000立方厘米
1立方米=1000立方分米
相邻的两个体积单位之间的进率是1000。
1dm =1000cm
1m =1000dm
计量容积,一般用体积单位;液体的体积,常用容积单位L和mL。
1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
容积和容积单位
1
选自教材第43页练习十
下面是同一个长方体的展开图,说一说每个图是怎样展开的。
上
左
右
前
后
下
上
右
前
后
下
左
找一些正方体纸盒将其展开,你能展开成多少种不同的形状?
“141”型
“231”型
“222”型
“33”型
2
长方体的长、宽、高都变为原来的 2 倍,它的表面积和体积分别发生了什么变化?你发现了什么规律?
长方体 长/cm 宽/cm 高/cm 表面积/cm2 体积/cm3
① 2 1 3
② 4 2 6
③ 8 4 12
22
6
88
48
352
384
规律:如果长方体的长、宽、高都变为原来的 2 倍,
它的表面积变为原来的 4 倍,体积变为原来的 8 倍。
3
一个长方体鱼塘长 8 m,宽 4.5 m,深 2 m。这个鱼塘的容积是多少?
8×4.5×2 = 72(m3)
答:这个鱼塘的容积是72立方米。
4
某古建筑景点定做了 25 个宫灯(如右图,单位:cm)。宫灯外侧有一层外饰面(上、下面除外)。如果外饰面每平方米18元,这些宫灯的外饰面一共要花多少钱?
18×50 = 900(元)
(66×20×4+46×80×4)×25
=(5280+14720)×25
= 500000(cm2)
= 50(m2)
答:这些宫灯的外饰面一共要花900元。
长方体有( )个面,( )个顶点,( )条棱,相对的两个面( )。一个长方体最多有( )个面完全相同。
6
8
12
完全相同
4
比较正方体有什么不同呢?
1.
一个长12厘米、宽8厘米、高5厘米的长方体,这个长方体六个面中最大面的面积是( )平方厘米,最小面的面积是( )平方厘米。
12厘米
8厘米
5厘米
长×宽
宽×高
96
40
2.
判断:
棱长是6分米的正方体的表面积和体积相等。
( )
体积和面积是两个不同的概念,两者单位不同,不能比较大小。
×
3.
一个菜窖能容纳6立方米白菜,说明这个菜窖的( )是6立方米。
A.体积 B.容积 C.表面积
B
所能容纳物体的体积,通常叫作它们的容积。
4.
(30×20+30×15+20×15)×2=2700(平方厘米)
答:需要2700平方厘米彩纸。
爸爸买了一个长30厘米、宽20厘米、高15厘米的长方体礼盒,里面装有妈妈爱吃的长方体形状的花生酥,每块花生酥长5厘米、宽3厘米、高2厘米。
(1)礼盒用彩纸包装,需要多少彩纸?(重叠部分不计算)
5.
长方体礼盒的表面积。
(30÷5)×(20÷2)×(15÷3)=300(块)
答:最多能装300块花生酥。
长方体的摆法不同,长、宽、高不同。
爸爸买了一个长30厘米、宽20厘米、高15厘米的长方体礼盒,里面装有妈妈爱吃的长方体形状的花生酥,每块花生酥长5厘米、宽3厘米、高2厘米。
(2)最多能装多少块花生酥?
5.
行数
列数
层数
× ×
这节课有什么收获呢?
在解决有关表面积的实际问题时,要根据具体情况确定要算哪几个面。
练习十
长方体表面积=(长×宽+长×高+宽×高)×2
正方体表面积=棱长×棱长×6
V=abh
V=a
V=Sh
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
1dm =1000cm
1m =1000dm
