五年级下册数学人教版3.4 整理和复习 课件(34张ppt)
文档属性
| 名称 | 五年级下册数学人教版3.4 整理和复习 课件(34张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 20:24:46 | ||
图片预览



文档简介
(共34张PPT)
整理和复习
第三单元 长方体和正方体
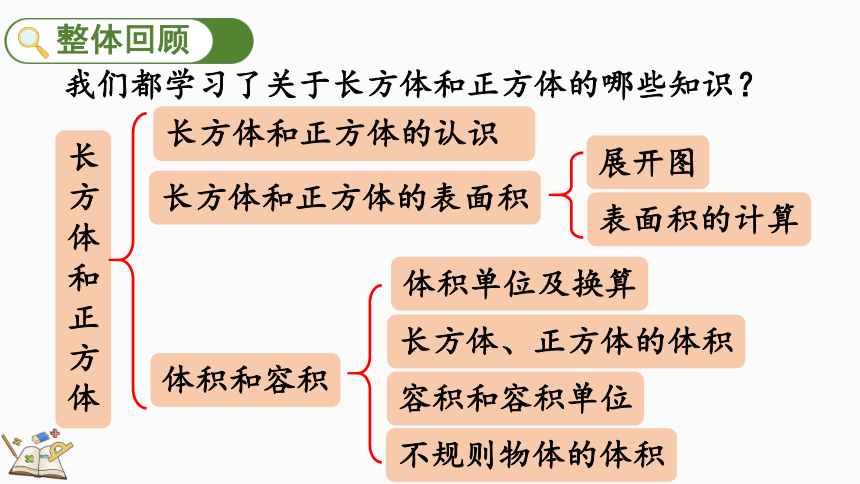
长方体和正方体
长方体和正方体的表面积
体积和容积
长方体和正方体的认识
体积单位及换算
长方体、正方体的体积
容积和容积单位
展开图
表面积的计算
不规则物体的体积
我们都学习了关于长方体和正方体的哪些知识?
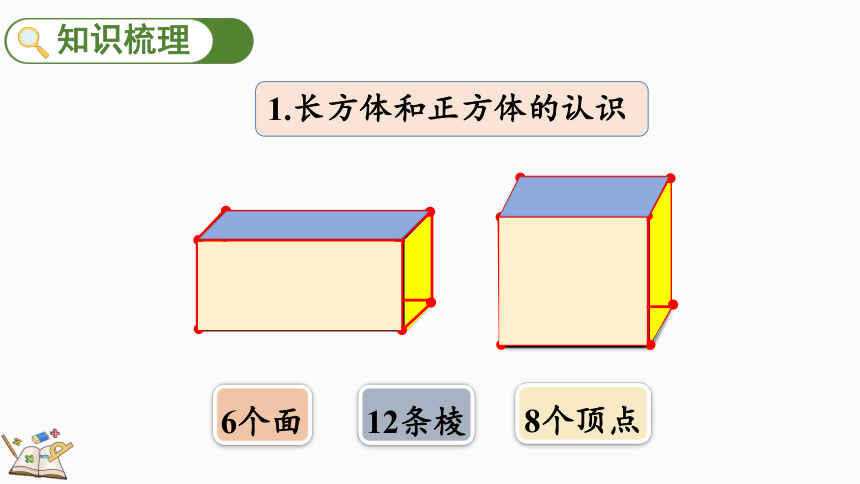
1.长方体和正方体的认识
12条棱
6个面
8个顶点
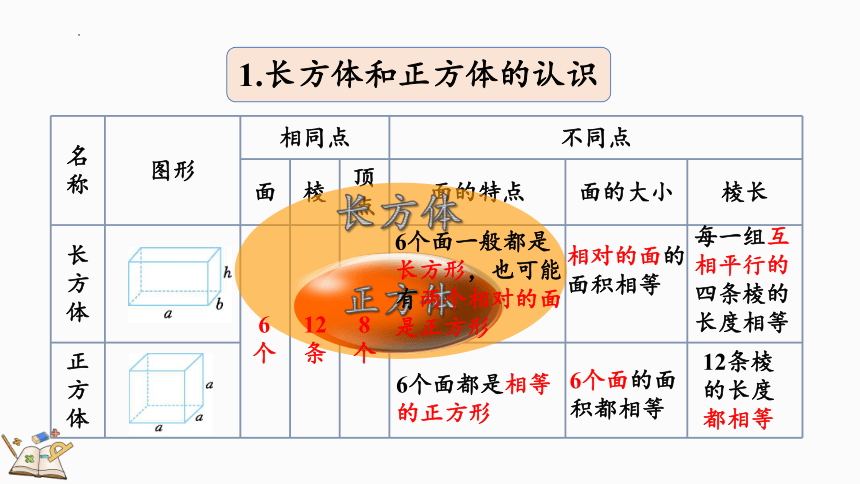
1.长方体和正方体的认识
名称 图形 相同点 不同点
面 棱 顶点 面的特点 面的大小 棱长
长方体
正方体
长方体
正方体
6个
12条
8个
6个面一般都是长方形,也可能有两个相对的面是正方形
6个面都是相等的正方形
相对的面的面积相等
6个面的面积都相等
每一组互相平行的四条棱的长度相等
12条棱的长度都相等
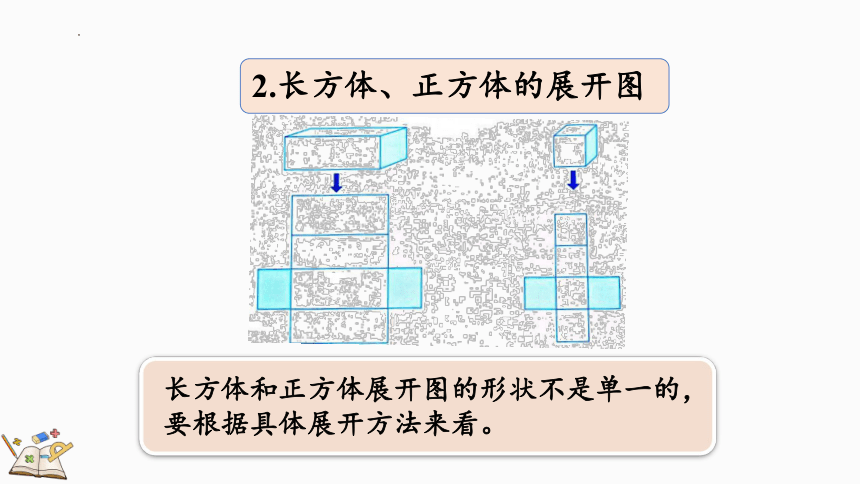
2.长方体、正方体的展开图
长方体和正方体展开图的形状不是单一的,要根据具体展开方法来看。
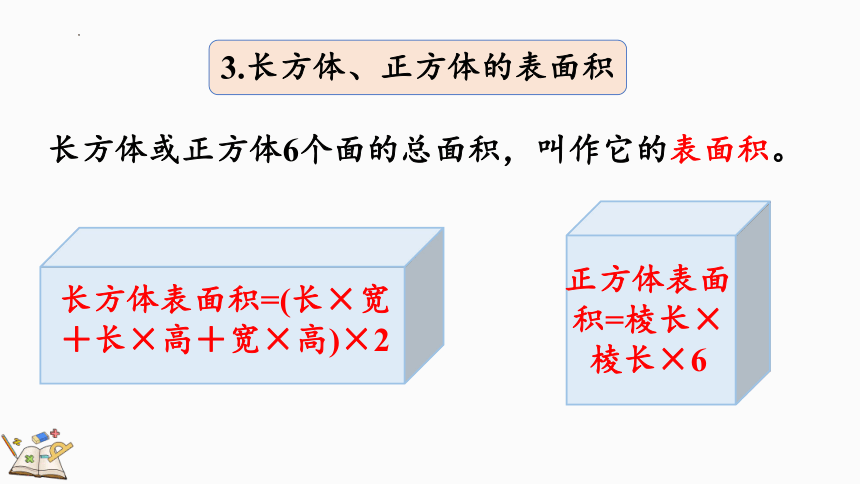
3.长方体、正方体的表面积
长方体表面积=(长×宽+长×高+宽×高)×2
正方体表面积=棱长×棱长×6
长方体或正方体6个面的总面积,叫作它的表面积。
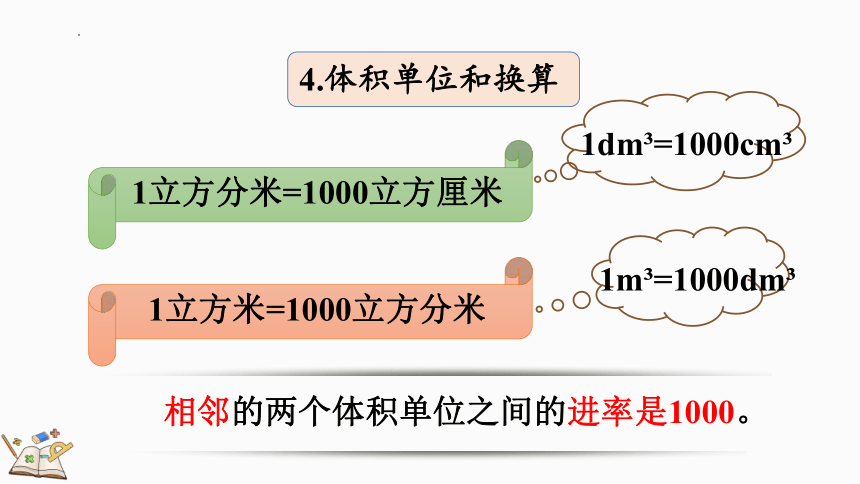
4.体积单位和换算
1立方分米=1000立方厘米
1立方米=1000立方分米
相邻的两个体积单位之间的进率是1000。
1dm =1000cm
1m =1000dm
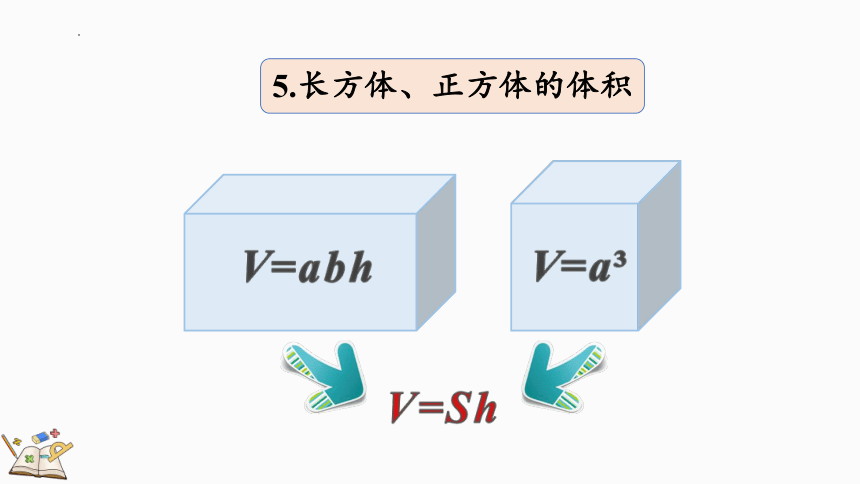
5.长方体、正方体的体积
V
=abh
V
=a
V=Sh
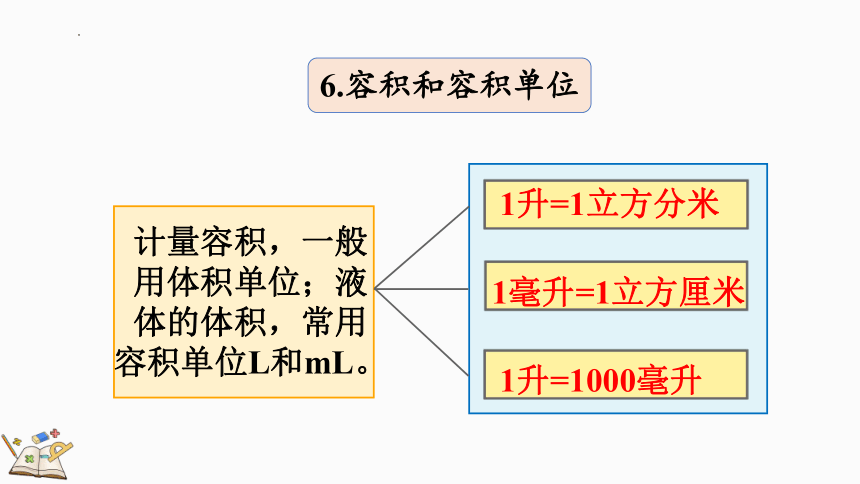
6.容积和容积单位
像太空舱、粮仓、油桶、盒子等所能容纳物体的体积,通常叫作它们的容积。
思考一下容积和体积的联系和区别。
计量容积,一般用体积单位;液体的体积,常用容积单位L和mL。
1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
6.容积和容积单位
7.不规则物体的体积
测量不规则物体的体积,通常采用排水法,即利用有刻度的量筒或量杯,记录下放入不规则物体前后水位的刻度,上升的那部分水的体积就是不规则物体的体积。
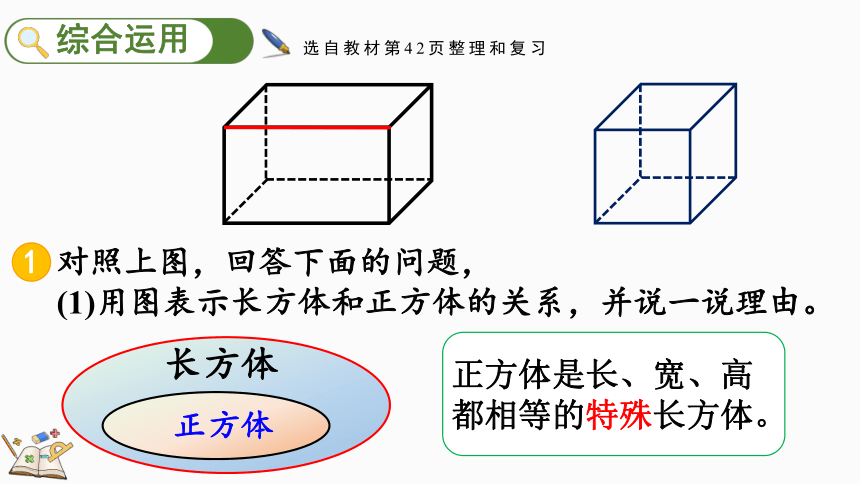
选自教材第42页整理和复习
1
对照上图,回答下面的问题,
(1)用图表示长方体和正方体的关系,并说一说理由。
长方体
正方体
正方体是长、宽、高都相等的特殊长方体。
1.长方体相对的棱平行且相等。
2.长、宽、高互相垂直。
(2)在上面的长方体中有一条红色标示的棱,分别
指出与它平行的棱和与它相交且垂直的棱,你
能发现什么?
(3)回忆计算表面积的方法以及探索体积公式的过程,
说一说关键是要知道什么。计算体积和容积有什
么相同点和不同点?
长方体或正方体6个面的总面积,叫作它的表面积。
长方体的表面积=S上+S下+S前+S后+S左+S右
=长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2
S表=2ab+2ah+2bh
宽(b)
长(a)
高(h)
S表=(ab+ah+bh)×2
S表=6a
棱长(a)
棱长(a)
棱长(a)
长方体的体积=长×宽×高
V = abh
正方体的体积=棱长×棱长×棱长
V = a3
宽(b)
长(a)
高(h)
长方体或正方体的体积=底面积×高
V = Sh
宽(b)
长(a)
高(h)
底面积(S)
关键是要知道长方体的长、宽、高和正方体的棱长。
体积与容积计算方法一样,物体形状规则时,测量有关数据,利用公式计算;物体形状不规则时,想办法转化为规则的,常用“排水法”转化。
体积和容积的单位不同。
(3)回忆计算表面积的方法以及探索体积公式的过程,
说一说关键是要知道什么。计算体积和容积有什
么相同点和不同点?
2
你能用尺子和长方体(或正方体)容器测出下面物体的体积吗?如果用这种方法比较两个物体体积的大小,你打算怎么做?
玻璃球可以用“排水法”,转化为规则的物体的体积。
绿豆也可以用“排水法”,但体积太小,水位上升不明显,可以多放一些绿豆在水中,如10粒、20粒,求出总体积后再除以10或20,得到每粒绿豆的体积。
玻璃球
绿豆
下面的长方体都是用棱长 1 cm 的小正方体摆成的。计算它们的体积。
下面的长方体都是用棱长 1 cm 的小正方体摆成的。计算它们的体积。
4cm
3cm
3cm
3×3×4=36(cm3)
4cm
4cm
4cm
4×4×4=64(cm3)
判断。对的画“√”,错的画“×”。
(1)长方体的横截面有可能是正方形。 ( )
√
×
(2)表面积相等的两个长方体,它们的体积一定
相等。 ( )
形状不一定相同,所以体积不一定相等。
1.
一个长8厘米、宽2厘米、高3厘米的长方体,这个长方体的棱长总和是( )厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
(长×宽+长×高+宽×高)×2
长方体有12条棱,分成4组,棱长总和=(长+宽+高)×4。
V= abh
52
92
48
2.
下图中甲的表面积( )乙的表面积。
A.大于 B.等于 C.小于
立体图形的所有面的面积之和是它的表面积。
B
3.
下面图形不能围成长方体的是( )。
C
长方体的展开图形状要根据展开的方法来确定。
4.
填空。
2.32 m3=( )dm3 8570 cm3=( )dm3
7.5 m3=( )dm3 9.6 dm2=( )cm2
530 cm3=( )dm3 43.3 dm3=( )cm3
87.2 cm2=( )dm2
7.62 L=( )mL
2320
8.57
7500
960
0.53
43300
0.872
7620
5.
一个无盖的长方体水箱,长2.5分米,宽2.5分米,高3.5分米。制作一个这样的水箱至少需要铁皮多少平方分米?
长方体表面积=(长×宽+长×高+宽×高)×2
长方体表面积=长×宽+(长×高+宽×高)×2
求表面积
水箱表面积=长×宽+长(宽)×高×4
6.
2.5×2.5+2.5×3.5×4
=6.25+35
=41.25(平方分米)
答:制作一个这样的水箱至少需要铁皮41.25平方分米。
求5个面的表面积。
一个无盖的长方体水箱,长2.5分米,宽2.5分米,高3.5分米。制作一个这样的水箱至少需要铁皮多少平方分米?
6.
一个长方体形状的游泳池,长50米,宽30米,深2米。这个游泳池能蓄水多少升?
50×30×2=3000(立方米)
3000立方米=3000000升
答:这个游泳池能蓄水3000000升。
7.
在一个长120厘米、宽60厘米的长方体水箱里,浸没一块长方体铁块后,水面上升了2厘米。求铁块的体积。
上升部分的水的体积就是铁块的体积。
120×60×2=14400(立方厘米)
答:铁块的体积是14400立方厘米。
8.
将棱长是1.6分米的正方体石块浸没到一个长方体水槽里,水面上升了3.2分米,然后放入一个铁块并浸没,水面又上升了0.9分米,求铁块的体积。
V
=a
V水
=Sh
S=V÷h
=V水
V石
a =1.6分米
h=3.2分米
9.
答:铁块的体积是1.152dm3。
石块体积:1.6×1.6×1.6=4.096(dm )
水槽底面积:4.096÷3.2=1.28(dm2)
铁块体积:1.28×0.9=1.152(dm3)
将棱长是1.6分米的正方体石块浸没到一个长方体水槽里,水面上升了3.2分米,然后放入一个铁块并浸没,水面又上升了0.9分米,求铁块的体积。
9.
长方体和正方体
长方体和正方体的表面积
体积和容积
长方体和正方体的认识
体积单位及换算
长方体、正方体的体积
容积和容积单位
展开图
表面积的计算
不规则物体的体积
整理和复习
整理和复习
第三单元 长方体和正方体
长方体和正方体
长方体和正方体的表面积
体积和容积
长方体和正方体的认识
体积单位及换算
长方体、正方体的体积
容积和容积单位
展开图
表面积的计算
不规则物体的体积
我们都学习了关于长方体和正方体的哪些知识?
1.长方体和正方体的认识
12条棱
6个面
8个顶点
1.长方体和正方体的认识
名称 图形 相同点 不同点
面 棱 顶点 面的特点 面的大小 棱长
长方体
正方体
长方体
正方体
6个
12条
8个
6个面一般都是长方形,也可能有两个相对的面是正方形
6个面都是相等的正方形
相对的面的面积相等
6个面的面积都相等
每一组互相平行的四条棱的长度相等
12条棱的长度都相等
2.长方体、正方体的展开图
长方体和正方体展开图的形状不是单一的,要根据具体展开方法来看。
3.长方体、正方体的表面积
长方体表面积=(长×宽+长×高+宽×高)×2
正方体表面积=棱长×棱长×6
长方体或正方体6个面的总面积,叫作它的表面积。
4.体积单位和换算
1立方分米=1000立方厘米
1立方米=1000立方分米
相邻的两个体积单位之间的进率是1000。
1dm =1000cm
1m =1000dm
5.长方体、正方体的体积
V
=abh
V
=a
V=Sh
6.容积和容积单位
像太空舱、粮仓、油桶、盒子等所能容纳物体的体积,通常叫作它们的容积。
思考一下容积和体积的联系和区别。
计量容积,一般用体积单位;液体的体积,常用容积单位L和mL。
1升=1立方分米
1毫升=1立方厘米
1升=1000毫升
6.容积和容积单位
7.不规则物体的体积
测量不规则物体的体积,通常采用排水法,即利用有刻度的量筒或量杯,记录下放入不规则物体前后水位的刻度,上升的那部分水的体积就是不规则物体的体积。
选自教材第42页整理和复习
1
对照上图,回答下面的问题,
(1)用图表示长方体和正方体的关系,并说一说理由。
长方体
正方体
正方体是长、宽、高都相等的特殊长方体。
1.长方体相对的棱平行且相等。
2.长、宽、高互相垂直。
(2)在上面的长方体中有一条红色标示的棱,分别
指出与它平行的棱和与它相交且垂直的棱,你
能发现什么?
(3)回忆计算表面积的方法以及探索体积公式的过程,
说一说关键是要知道什么。计算体积和容积有什
么相同点和不同点?
长方体或正方体6个面的总面积,叫作它的表面积。
长方体的表面积=S上+S下+S前+S后+S左+S右
=长×宽×2+长×高×2+宽×高×2
=(长×宽+长×高+宽×高)×2
S表=2ab+2ah+2bh
宽(b)
长(a)
高(h)
S表=(ab+ah+bh)×2
S表=6a
棱长(a)
棱长(a)
棱长(a)
长方体的体积=长×宽×高
V = abh
正方体的体积=棱长×棱长×棱长
V = a3
宽(b)
长(a)
高(h)
长方体或正方体的体积=底面积×高
V = Sh
宽(b)
长(a)
高(h)
底面积(S)
关键是要知道长方体的长、宽、高和正方体的棱长。
体积与容积计算方法一样,物体形状规则时,测量有关数据,利用公式计算;物体形状不规则时,想办法转化为规则的,常用“排水法”转化。
体积和容积的单位不同。
(3)回忆计算表面积的方法以及探索体积公式的过程,
说一说关键是要知道什么。计算体积和容积有什
么相同点和不同点?
2
你能用尺子和长方体(或正方体)容器测出下面物体的体积吗?如果用这种方法比较两个物体体积的大小,你打算怎么做?
玻璃球可以用“排水法”,转化为规则的物体的体积。
绿豆也可以用“排水法”,但体积太小,水位上升不明显,可以多放一些绿豆在水中,如10粒、20粒,求出总体积后再除以10或20,得到每粒绿豆的体积。
玻璃球
绿豆
下面的长方体都是用棱长 1 cm 的小正方体摆成的。计算它们的体积。
下面的长方体都是用棱长 1 cm 的小正方体摆成的。计算它们的体积。
4cm
3cm
3cm
3×3×4=36(cm3)
4cm
4cm
4cm
4×4×4=64(cm3)
判断。对的画“√”,错的画“×”。
(1)长方体的横截面有可能是正方形。 ( )
√
×
(2)表面积相等的两个长方体,它们的体积一定
相等。 ( )
形状不一定相同,所以体积不一定相等。
1.
一个长8厘米、宽2厘米、高3厘米的长方体,这个长方体的棱长总和是( )厘米,它的表面积是( )平方厘米,体积是( )立方厘米。
(长×宽+长×高+宽×高)×2
长方体有12条棱,分成4组,棱长总和=(长+宽+高)×4。
V= abh
52
92
48
2.
下图中甲的表面积( )乙的表面积。
A.大于 B.等于 C.小于
立体图形的所有面的面积之和是它的表面积。
B
3.
下面图形不能围成长方体的是( )。
C
长方体的展开图形状要根据展开的方法来确定。
4.
填空。
2.32 m3=( )dm3 8570 cm3=( )dm3
7.5 m3=( )dm3 9.6 dm2=( )cm2
530 cm3=( )dm3 43.3 dm3=( )cm3
87.2 cm2=( )dm2
7.62 L=( )mL
2320
8.57
7500
960
0.53
43300
0.872
7620
5.
一个无盖的长方体水箱,长2.5分米,宽2.5分米,高3.5分米。制作一个这样的水箱至少需要铁皮多少平方分米?
长方体表面积=(长×宽+长×高+宽×高)×2
长方体表面积=长×宽+(长×高+宽×高)×2
求表面积
水箱表面积=长×宽+长(宽)×高×4
6.
2.5×2.5+2.5×3.5×4
=6.25+35
=41.25(平方分米)
答:制作一个这样的水箱至少需要铁皮41.25平方分米。
求5个面的表面积。
一个无盖的长方体水箱,长2.5分米,宽2.5分米,高3.5分米。制作一个这样的水箱至少需要铁皮多少平方分米?
6.
一个长方体形状的游泳池,长50米,宽30米,深2米。这个游泳池能蓄水多少升?
50×30×2=3000(立方米)
3000立方米=3000000升
答:这个游泳池能蓄水3000000升。
7.
在一个长120厘米、宽60厘米的长方体水箱里,浸没一块长方体铁块后,水面上升了2厘米。求铁块的体积。
上升部分的水的体积就是铁块的体积。
120×60×2=14400(立方厘米)
答:铁块的体积是14400立方厘米。
8.
将棱长是1.6分米的正方体石块浸没到一个长方体水槽里,水面上升了3.2分米,然后放入一个铁块并浸没,水面又上升了0.9分米,求铁块的体积。
V
=a
V水
=Sh
S=V÷h
=V水
V石
a =1.6分米
h=3.2分米
9.
答:铁块的体积是1.152dm3。
石块体积:1.6×1.6×1.6=4.096(dm )
水槽底面积:4.096÷3.2=1.28(dm2)
铁块体积:1.28×0.9=1.152(dm3)
将棱长是1.6分米的正方体石块浸没到一个长方体水槽里,水面上升了3.2分米,然后放入一个铁块并浸没,水面又上升了0.9分米,求铁块的体积。
9.
长方体和正方体
长方体和正方体的表面积
体积和容积
长方体和正方体的认识
体积单位及换算
长方体、正方体的体积
容积和容积单位
展开图
表面积的计算
不规则物体的体积
整理和复习
