人教版五年级下册数学4.5.2 公倍数和最小公倍数的应用 课件(16张ppt)
文档属性
| 名称 | 人教版五年级下册数学4.5.2 公倍数和最小公倍数的应用 课件(16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 20:31:33 | ||
图片预览




文档简介
(共16张PPT)
公倍数和最小公倍数的应用
第四单元 分数的意义和性质
规则:
1.第一组的同学从1开始报数;
2.听到2的倍数举左手,听到3的倍数举右手,听到2和3的公倍数拍拍手。
报数游戏
一种长方形地砖长3 dm,宽2 dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块的),正方形的边长可以是多少分米?最小是多少分米?
阅读与理解
你知道哪些信息?
3dm
2dm
dm
dm
3dm
2dm
3
dm
dm
3dm
2dm
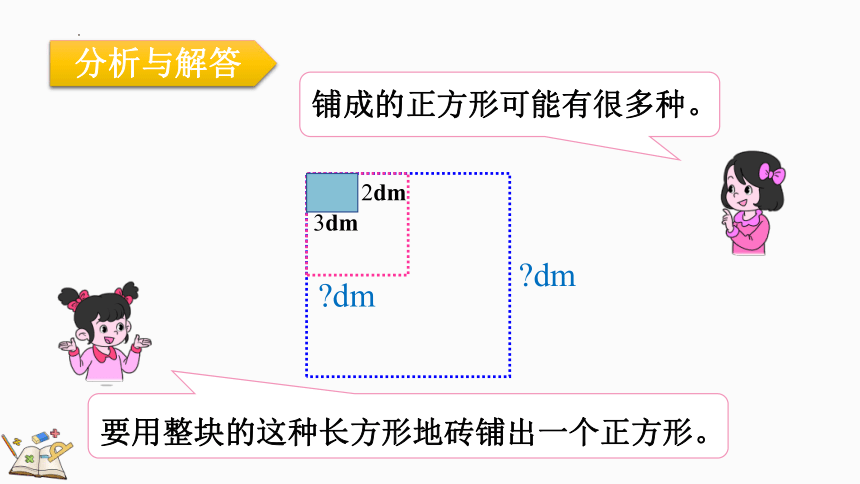
要用整块的这种长方形地砖铺出一个正方形。
铺成的正方形可能有很多种。
分析与解答
分析与解答
边长
是地砖长3 dm的倍数。
边长
是地砖宽2 dm的倍数。
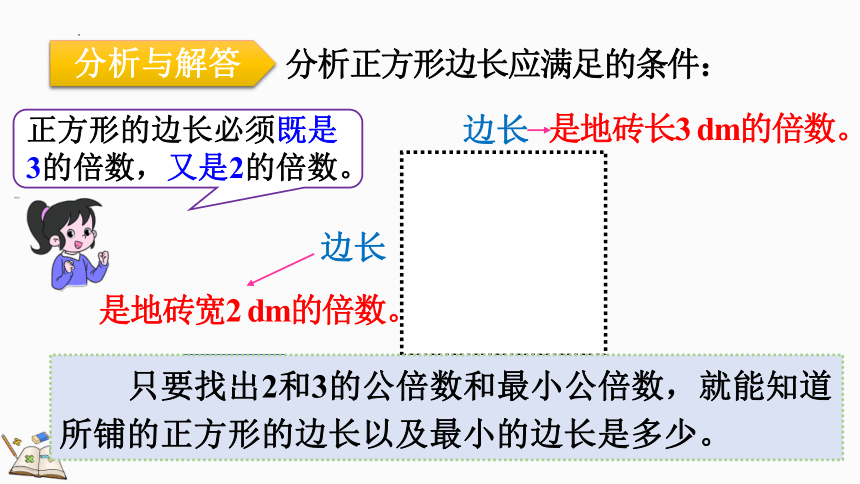
分析正方形边长应满足的条件:
正方形的边长必须既是3的倍数,又是2的倍数。
只要找出2和3的公倍数和最小公倍数,就能知道所铺的正方形的边长以及最小的边长是多少。
2的倍数有:2, 4, 6, 8, 10, 12, 14, 16, 18, …
3的倍数有:3, 6, 9, 12, 15, 18, …
2和3的公倍数有:6, 12, 18, …,最小公倍数是6。
所以,正方形的边长可以是6 dm,12 dm,18 dm, …;边长最小是6 dm。
分析与解答
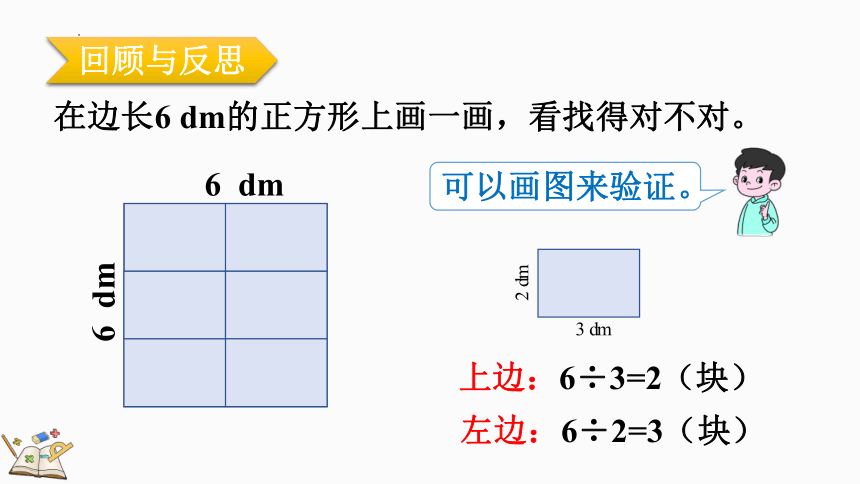
回顾与反思
在边长6 dm的正方形上画一画,看找得对不对。
可以画图来验证。
6 dm
6 dm
上边:6÷3=2(块)
3 dm
2 dm
左边:6÷2=3(块)
在边长12 dm的正方形上画一画,看找得对不对。
12 dm
12 dm
上边:12÷3=4(块)
左边:12÷2=6(块)
3 dm
2 dm
回顾与反思
怎样解决铺地砖问题?
解决地砖铺正方形问题的关键是把铺砖问题转化为求公倍数的问题。要使用的地砖必须都是整块,则铺成的正方形边长必须是地砖长和宽的公倍数。要求最小的正方形边长就是求地砖长与宽的最小公倍数。
当所求量分别与两个(或几个)已知量的倍数有关时,可以用公倍数或最小公倍数的知识解决。
说一说
选自教材第70页做一做
1
参加跳绳比赛的学生分组进行计数,可以6人一组,也可以9人一组,都正好分完。如果这些学生的总人数在40人以内,可能是多少人?
学生人数是40以内的6和9的公倍数。
9的倍数有9,18,27,36,45,54,…
18<40, 36<40, 54>40, …
答:可能是18人或36人。
有一堆糖,4颗4颗地数,6颗6颗地数,都能刚好数完。这堆糖至少有多少颗?
这堆糖的最少颗数是4和6的最小公倍数。
答:这堆糖至少有12颗。
2
一个长方形的长和宽分别是24cm和9cm,至少多少个这样的长方形才能拼成一个正方形?这个正方形的边长是多少?
24 9
3
8 3
3×8×3=72(cm)
长:72÷24=3 宽:72÷9=8
3×8=24(个)
答:至少用24个长方形,正方形的边长是72cm。
1
暑假期间,汪老师每4天到校一次,张老师每6天到校一次。如果7月10日他俩同时到校,下次两人同一天到校是几月几日?
从这次同一天到校到下一次同一天到校,经过的天数是4和6的最小公倍数。
2
4和6的最小公倍数是12。
所以下次两人同一天到校是7月22日。
小明和爸爸、妈妈绕着环形湖边小道跑步,小明跑一圈要8分钟,爸爸跑一圈要4分钟,妈妈跑一圈要5分钟。他们同时同地出发,同向而行,多少时间后三人同时回到出发点?此时三人各跑了多少圈?
8、4、5的最小公倍数是40。
小明:
40÷8=5(圈)
爸爸:
40÷4=10(圈)
妈妈:
40÷5=8(圈)
答:至少过40分钟三人同时回到出发点,小明跑了5圈,爸爸跑了10圈,妈妈跑了8圈。
这节课有什么收获呢?
利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一天到达问题等等。
公倍数和最小公倍数的应用
公倍数和最小公倍数的应用
6 dm
6 dm
边长
是地砖长3 dm的倍数。
边长
是地砖宽2 dm的倍数。
正方形的边长必须既是3的倍数,又是2的倍数。
公倍数和最小公倍数的应用
第四单元 分数的意义和性质
规则:
1.第一组的同学从1开始报数;
2.听到2的倍数举左手,听到3的倍数举右手,听到2和3的公倍数拍拍手。
报数游戏
一种长方形地砖长3 dm,宽2 dm。如果用这种地砖铺一个正方形(用的地砖必须都是整块的),正方形的边长可以是多少分米?最小是多少分米?
阅读与理解
你知道哪些信息?
3dm
2dm
dm
dm
3dm
2dm
3
dm
dm
3dm
2dm
要用整块的这种长方形地砖铺出一个正方形。
铺成的正方形可能有很多种。
分析与解答
分析与解答
边长
是地砖长3 dm的倍数。
边长
是地砖宽2 dm的倍数。
分析正方形边长应满足的条件:
正方形的边长必须既是3的倍数,又是2的倍数。
只要找出2和3的公倍数和最小公倍数,就能知道所铺的正方形的边长以及最小的边长是多少。
2的倍数有:2, 4, 6, 8, 10, 12, 14, 16, 18, …
3的倍数有:3, 6, 9, 12, 15, 18, …
2和3的公倍数有:6, 12, 18, …,最小公倍数是6。
所以,正方形的边长可以是6 dm,12 dm,18 dm, …;边长最小是6 dm。
分析与解答
回顾与反思
在边长6 dm的正方形上画一画,看找得对不对。
可以画图来验证。
6 dm
6 dm
上边:6÷3=2(块)
3 dm
2 dm
左边:6÷2=3(块)
在边长12 dm的正方形上画一画,看找得对不对。
12 dm
12 dm
上边:12÷3=4(块)
左边:12÷2=6(块)
3 dm
2 dm
回顾与反思
怎样解决铺地砖问题?
解决地砖铺正方形问题的关键是把铺砖问题转化为求公倍数的问题。要使用的地砖必须都是整块,则铺成的正方形边长必须是地砖长和宽的公倍数。要求最小的正方形边长就是求地砖长与宽的最小公倍数。
当所求量分别与两个(或几个)已知量的倍数有关时,可以用公倍数或最小公倍数的知识解决。
说一说
选自教材第70页做一做
1
参加跳绳比赛的学生分组进行计数,可以6人一组,也可以9人一组,都正好分完。如果这些学生的总人数在40人以内,可能是多少人?
学生人数是40以内的6和9的公倍数。
9的倍数有9,18,27,36,45,54,…
18<40, 36<40, 54>40, …
答:可能是18人或36人。
有一堆糖,4颗4颗地数,6颗6颗地数,都能刚好数完。这堆糖至少有多少颗?
这堆糖的最少颗数是4和6的最小公倍数。
答:这堆糖至少有12颗。
2
一个长方形的长和宽分别是24cm和9cm,至少多少个这样的长方形才能拼成一个正方形?这个正方形的边长是多少?
24 9
3
8 3
3×8×3=72(cm)
长:72÷24=3 宽:72÷9=8
3×8=24(个)
答:至少用24个长方形,正方形的边长是72cm。
1
暑假期间,汪老师每4天到校一次,张老师每6天到校一次。如果7月10日他俩同时到校,下次两人同一天到校是几月几日?
从这次同一天到校到下一次同一天到校,经过的天数是4和6的最小公倍数。
2
4和6的最小公倍数是12。
所以下次两人同一天到校是7月22日。
小明和爸爸、妈妈绕着环形湖边小道跑步,小明跑一圈要8分钟,爸爸跑一圈要4分钟,妈妈跑一圈要5分钟。他们同时同地出发,同向而行,多少时间后三人同时回到出发点?此时三人各跑了多少圈?
8、4、5的最小公倍数是40。
小明:
40÷8=5(圈)
爸爸:
40÷4=10(圈)
妈妈:
40÷5=8(圈)
答:至少过40分钟三人同时回到出发点,小明跑了5圈,爸爸跑了10圈,妈妈跑了8圈。
这节课有什么收获呢?
利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一天到达问题等等。
公倍数和最小公倍数的应用
公倍数和最小公倍数的应用
6 dm
6 dm
边长
是地砖长3 dm的倍数。
边长
是地砖宽2 dm的倍数。
正方形的边长必须既是3的倍数,又是2的倍数。
