五年级下册数学人教版5.3 练习二十一(课件)(共25张PPT)
文档属性
| 名称 | 五年级下册数学人教版5.3 练习二十一(课件)(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 20:44:01 | ||
图片预览






文档简介
(共25张PPT)
练习二十一
第五单元 图形的运动(三)
还记得描述图形的旋转时,要注意什么吗?
描述物体的旋转时,一定要说清旋转中心、旋转方向和旋转角度。
说一说:下面的指针是怎么旋转的?
指针从“2”绕中心点顺时针旋转30°到了“3”。
指针从“3”绕中心点逆时针旋转360°到了“3”。
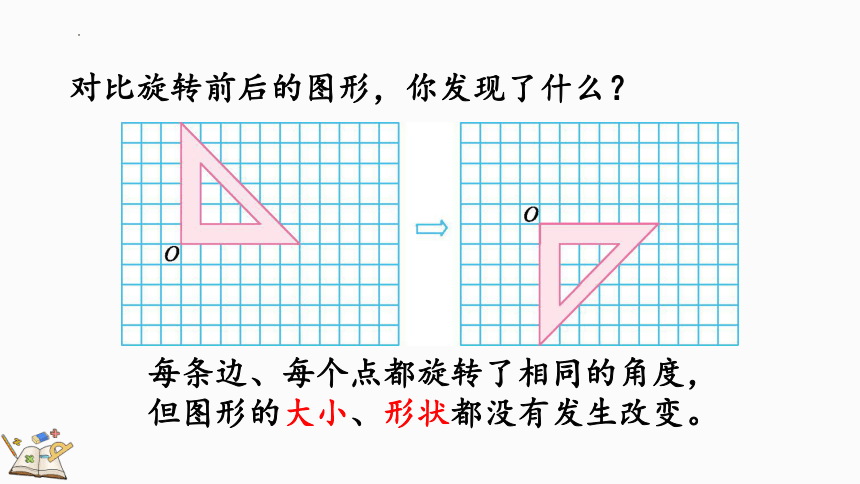
每条边、每个点都旋转了相同的角度,
但图形的大小、形状都没有发生改变。
对比旋转前后的图形,你发现了什么?
想一想:在方格纸上画旋转后的图形的步骤是什么?
确定所给图形的关键点;
确定关键点到旋转点的距离;
确定关键点的对应点;
把描出的对应点按顺序连线。
1
选自教材第85~86页练习二十一
下面的图案分别是由哪个图形旋转而成的?
分别由图中涂色部分顺时针或逆时针旋转而成。
2
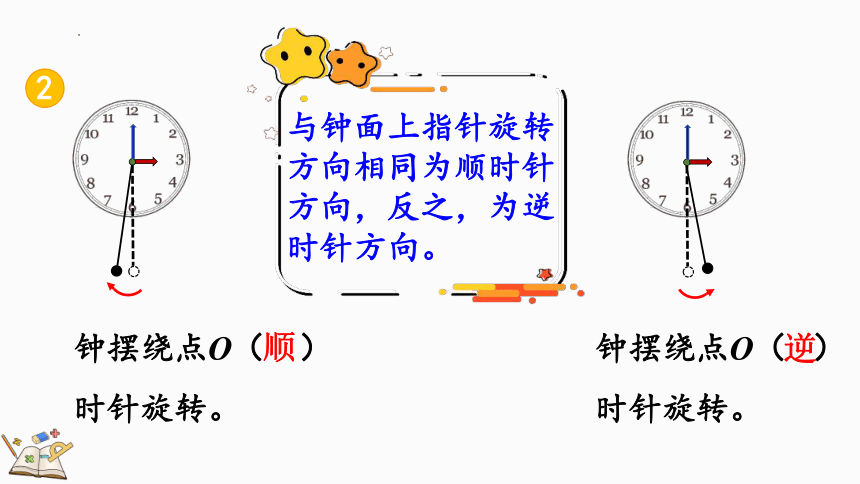
钟摆绕点O( )时针旋转。
顺
钟摆绕点O( )时针旋转。
逆
与钟面上指针旋转方向相同为顺时针方向,反之,为逆时针方向。
3
风车绕点 O
( )时针旋转_____ 。
风车绕点 O
( )时针旋转_____。
逆
90°
逆
90°
4
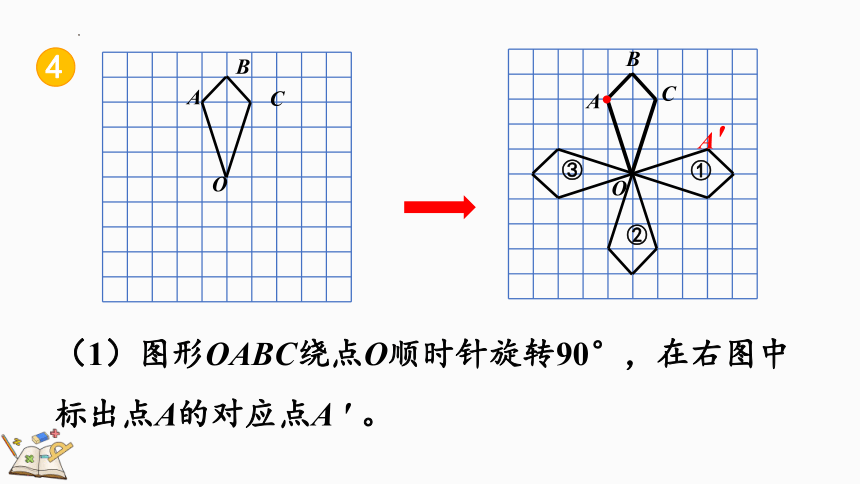
(1)图形OABC绕点O顺时针旋转90°,在右图中标出点A的对应点A ′ 。
A
B
C
O
A
O
③
②
①
A′
B
C
(2)图形OABC绕点O( )时针旋转 ,得到图② 。
A
B
C
O
A
O
③
②
①
顺
180°
图形OABC还可以绕点O逆时针旋转180°,得到图② 。
B
C
4
(3)图形OABC绕点O( )时针旋转 ,得到图③ 。
A
B
C
O
A
O
③
②
①
顺
270°
图形OABC还可以绕点O逆时针旋转90°,得到图③ 。
B
C
4
5
O
①
②
③
④
(1)把图①绕点O 逆时针旋转90°,得到图②。
(2)把图①绕点O 顺时针旋转90°,得到图③。
(3)把图②绕点O 逆时针旋转90°,得到图④。
(4)把图①、图②、图③、图④都涂上红色,这个图形像什么?
这个图形像风车。
按要求画图。
6
如图,长方形的两条对称轴相交于点O。绕点O旋转长方形,你能发现什么?
旋转90°
旋转180°
旋转360°
发现:长方形绕点O旋转180°的整数倍后,与原来的长方形重合。
将下列图形按上面的方法试一试,你能发现什么?
6
旋转30°
旋转60°
旋转120°
O
O
O
O
正六边形绕其对称轴的交点点O旋转60°的整数倍后,与原图重合。
6
O
O
旋转60°
O
旋转120°
O
旋转360°
等边三角形绕其对称轴的交点点O旋转120°的整数倍后,与原图重合。
6
O
O
旋转45°
O
旋转90°
O
旋转180°
圆形绕其对称轴的交点点O旋转任意角度后,与原图重合。
6
旋转45°
旋转90°
旋转180°
正边形绕其对称轴的交点点O旋转90°的整数倍后,与原图重合。
O
6
如果某一图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形。常见的旋转对称图形包括线段、圆、等边三角形、长方形、正方形等。
6
看图填空。
(1)指针从“12”绕点O逆时针旋转( )到“9”。
(2)指针从“9”绕点O顺时针旋转180°到( )。
90°
“3”
1
A
B
图形A绕点C顺时针旋转180°
向下平移
向左平移就得到图形B了
180°
C
.
如下图,图形A怎样变换能得到图形B?
2
先画出三角形ABC关于BC所在直线对称的轴对称图形A′BC ,再画出三角形A′BC绕点C逆时针旋转90°,向右平移3格后的三角形A 〞 B′C′。
A
B
C
3
格
3
格
A′
A 〞
B′
C′
3
你知道吗?
数学与艺术
设计师们利用几何学中的平移、对称和旋转,设计出了许多美丽的图案。
这节课有什么收获呢?
在观察图形的变换时,要多角度思考,图形的变换不只是单纯的一种,有时是多种变换的结合。
练习二十一
图形旋转位置变化,
形状、大小不变。
对应点、线随图转动,
对应角度不变。
练习二十一
第五单元 图形的运动(三)
还记得描述图形的旋转时,要注意什么吗?
描述物体的旋转时,一定要说清旋转中心、旋转方向和旋转角度。
说一说:下面的指针是怎么旋转的?
指针从“2”绕中心点顺时针旋转30°到了“3”。
指针从“3”绕中心点逆时针旋转360°到了“3”。
每条边、每个点都旋转了相同的角度,
但图形的大小、形状都没有发生改变。
对比旋转前后的图形,你发现了什么?
想一想:在方格纸上画旋转后的图形的步骤是什么?
确定所给图形的关键点;
确定关键点到旋转点的距离;
确定关键点的对应点;
把描出的对应点按顺序连线。
1
选自教材第85~86页练习二十一
下面的图案分别是由哪个图形旋转而成的?
分别由图中涂色部分顺时针或逆时针旋转而成。
2
钟摆绕点O( )时针旋转。
顺
钟摆绕点O( )时针旋转。
逆
与钟面上指针旋转方向相同为顺时针方向,反之,为逆时针方向。
3
风车绕点 O
( )时针旋转_____ 。
风车绕点 O
( )时针旋转_____。
逆
90°
逆
90°
4
(1)图形OABC绕点O顺时针旋转90°,在右图中标出点A的对应点A ′ 。
A
B
C
O
A
O
③
②
①
A′
B
C
(2)图形OABC绕点O( )时针旋转 ,得到图② 。
A
B
C
O
A
O
③
②
①
顺
180°
图形OABC还可以绕点O逆时针旋转180°,得到图② 。
B
C
4
(3)图形OABC绕点O( )时针旋转 ,得到图③ 。
A
B
C
O
A
O
③
②
①
顺
270°
图形OABC还可以绕点O逆时针旋转90°,得到图③ 。
B
C
4
5
O
①
②
③
④
(1)把图①绕点O 逆时针旋转90°,得到图②。
(2)把图①绕点O 顺时针旋转90°,得到图③。
(3)把图②绕点O 逆时针旋转90°,得到图④。
(4)把图①、图②、图③、图④都涂上红色,这个图形像什么?
这个图形像风车。
按要求画图。
6
如图,长方形的两条对称轴相交于点O。绕点O旋转长方形,你能发现什么?
旋转90°
旋转180°
旋转360°
发现:长方形绕点O旋转180°的整数倍后,与原来的长方形重合。
将下列图形按上面的方法试一试,你能发现什么?
6
旋转30°
旋转60°
旋转120°
O
O
O
O
正六边形绕其对称轴的交点点O旋转60°的整数倍后,与原图重合。
6
O
O
旋转60°
O
旋转120°
O
旋转360°
等边三角形绕其对称轴的交点点O旋转120°的整数倍后,与原图重合。
6
O
O
旋转45°
O
旋转90°
O
旋转180°
圆形绕其对称轴的交点点O旋转任意角度后,与原图重合。
6
旋转45°
旋转90°
旋转180°
正边形绕其对称轴的交点点O旋转90°的整数倍后,与原图重合。
O
6
如果某一图形围绕某一点旋转一定的角度(小于360°)后能与原图形重合,那么这个图形就叫做旋转对称图形。常见的旋转对称图形包括线段、圆、等边三角形、长方形、正方形等。
6
看图填空。
(1)指针从“12”绕点O逆时针旋转( )到“9”。
(2)指针从“9”绕点O顺时针旋转180°到( )。
90°
“3”
1
A
B
图形A绕点C顺时针旋转180°
向下平移
向左平移就得到图形B了
180°
C
.
如下图,图形A怎样变换能得到图形B?
2
先画出三角形ABC关于BC所在直线对称的轴对称图形A′BC ,再画出三角形A′BC绕点C逆时针旋转90°,向右平移3格后的三角形A 〞 B′C′。
A
B
C
3
格
3
格
A′
A 〞
B′
C′
3
你知道吗?
数学与艺术
设计师们利用几何学中的平移、对称和旋转,设计出了许多美丽的图案。
这节课有什么收获呢?
在观察图形的变换时,要多角度思考,图形的变换不只是单纯的一种,有时是多种变换的结合。
练习二十一
图形旋转位置变化,
形状、大小不变。
对应点、线随图转动,
对应角度不变。
