五年级下册数学人教版9.7 总复习练习二十八 课件(44张ppt)
文档属性
| 名称 | 五年级下册数学人教版9.7 总复习练习二十八 课件(44张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-31 00:00:00 | ||
图片预览











文档简介
(共44张PPT)
练习二十八
第九单元 总复习
通过本学期的学习与复习,你学会了什么?
1.认识了因数和倍数。
2.学会了长方体和正方体表面积以及体积的计算方法,并能够运用知识解决问题。
3.学会了从不同角度观察物体,根据图形判断观察物体方向。
4.知道了分数的意义和性质,根据分数的性质进行约分、通分,能进行分数加减运算。
通过本学期的学习与复习,你学会了什么?
5.进一步加深对轴对称图形、平移以及旋转的认识。
6.认识了折线统计图,对于数据的记录,能够选择恰当的统计图进行统计。
7.学习“找次品”问题,能解决实际困难。
通过本学期的学习与复习,你学会了什么?
1
选自教材第118~121页练习二十八
下面哪些数是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是质数?哪些是合数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56
79
87
195
204
630
22
31
57
65
78
83
个位上是0,2,4,6或8的数都是2的倍数。
2的倍数:56、204、630、22、78;
5的倍数:195、630、65。
3的倍数:87、195、204、630、57、78;
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
个位上是0或5的数都是5的倍数。
56
79
87
195
204
630
22
31
57
65
78
83
一个数,如果只有1和它本身两个因数,这样的数叫作质数。
质数:79、31、83;
奇数:79、87、195、31、57、65、83;
合数:56、87、195、204、630、22、57、65、78;
一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。
整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数。
偶数:56、204、630、22、78。
2
(1)两个合数相乘,积还是合数。
两个合数、1和积本身都是积的因数,所以积还是合数。
判断下面的说法是否正确,并说一说你的理由。
(2)两个不同质数的公因数只有1。
(3)一个数的因数一定比它的倍数小。
正确
正确
一个数的最大因数等于它的最小倍数。
不正确
质数的因数只有1和它本身,所以两个不同质数的公因数只有1。
判断下面的说法是否正确,并说一说你的理由。
(4)两个数的最小公倍数是这两个数最大公因数的倍数。
(5)最小的质数是1。
正确
1既不是质数,也不是合数。
不正确
因为两个数的最小公倍数是其中任何一个数的倍数,两个数的最大公因数是其中任何一个数的因数,所以两个数的最小公倍数是两个数最大公因数的倍数。
2
3
找出下面每组数的最大公因数和最小公倍数,以其中一组为例,说一说你是怎样找到的。
4和5
6和16
15和20
10和8
3和9
4和5的最大公因数是1,最小公倍数是20;
6和16的最大公因数是2,最小公倍数是48;
15和20的最大公因数是5,最小公倍数是60;
10和8的最大公因数是2,最小公倍数是40;
3和9的最大公因数是3,最小公倍数是9。
求两个数的最大公因数和最小公倍数常用的方法有:列举法、筛选法、分解质因数法和短除法。
例如,
15 20
5
3
4
15和20的最大公因数是5,最小公倍数是5×3×4=60。
用公有的质因数连续去除
除到两个数的商是互质数为止
所有除数的积
所有除数和商的积
4
食品店有70多个松花蛋。如果把它们装进4个一排的蛋托中,正好装完;如果把它装进6个一排的蛋托中,也正好装完。一共有多少个松花蛋?
答:一共有72个松花蛋。
4和6的公倍数有:12,24,36,48,60,72,84……
已知食品店有70多个松花蛋,所以应该有72个松花蛋。
5
(1)把 4 m长的绳子平均剪成5段,每段长 m,
每段绳子是全长的 。
(2)1985 年第二次大熊猫调查结果显示,全国共有1114只野生大熊猫。2015 年第四次大熊猫调查结果显示,
5
4
5
1
全国共有1864只野生大熊猫,其中1387只生活在四川。第二次调查到的野生大熊猫数量是第四次调查数量的 ;根据第四次调查,生活在四川的野生大熊猫占所有野生大熊猫数量的 。
932
557
1864
1387
0
1
2
3
4
6
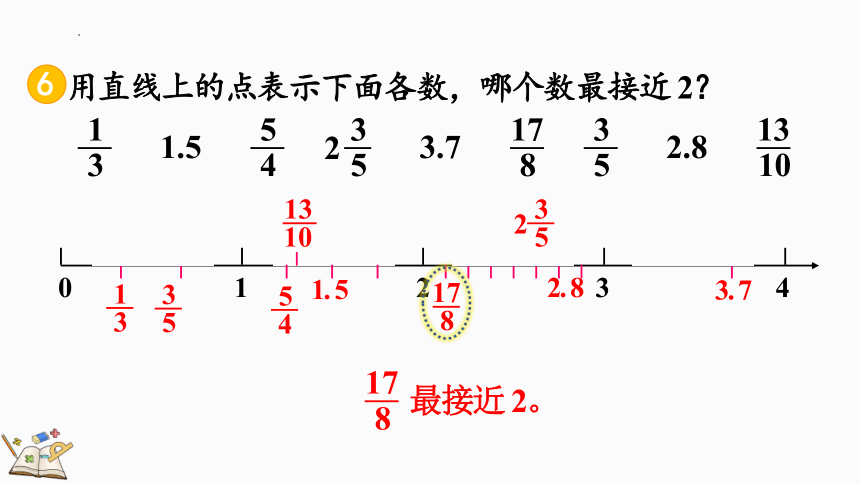
用直线上的点表示下面各数,哪个数最接近 2?
1.5
3
1
4
5
1. 5
3
1
8
17
4
5
5
3
5
3
2
10
13
3.7
2.8
3. 7
8
17
2. 8
5
3
10
13
8
17
最接近 2。
5
3
2
7
先填空,再把各数按从小到大的顺序排列起来。
2
7
=
( )
21
9
12
=
3
( )
5÷3= =1
( )
( )
( )
( )
2=
( )
( )
6
4
5
3
2
3
2
1
2
7
< <5÷3<2
9
12
8
下列分数中哪些是最简分数?把不是最简分数的化成最简分数,并说一说化简的依据。
6
8
36
16
10
21
30
45
12
25
5
7
72
6
最简分数有: 、 、 。其余的都不是最简分数,
根据分数的基本性质化简分数:
10
21
12
25
5
7
6
8
=
3
4
36
16
=
9
4
30
45
=
2
3
72
6
=12
9
计算。
10
3
+
10
7
=
10
10
= 1
6
5
-
6
1
=
6
4
=
3
2
7
4
-
3
1
=
21
12
-
21
7
=
21
5
6
1
5
1
2
1
+
+
=
30
5
+
30
6
+
30
15
=
30
26
=
15
13
计算。
8
7
-
4
3
=
8
7
-
8
6
=
8
1
3
2
+
9
7
=
9
6
+
9
7
=
9
13
7
-
3
5
=
3
21
-
3
5
=
3
16
6
-( - )
4
3
5
2
=
20
120
-( )
20
15
-
20
8
=
20
120
-
20
7
=
20
113
9
10
中国煤炭资源的种类较多,具体构成如右图。
(1)褐煤占煤炭总量的几分之几?
(2)你还能提出其他数学问题并解答吗?
(1)1- - =
3
4
3
25
13
100
答:褐煤占煤炭总量的 。
13
100
10
中国煤炭资源的种类较多,具体构成如右图。
(1)褐煤占煤炭总量的几分之几?
(2)你还能提出其他数学问题并解答吗?
(2)参考答案:
问:烟煤比无烟煤多占煤炭总量的几分之几?
- =
3
4
3
25
63
100
答:烟煤比无烟煤多占煤炭总量的 。
63
100
11
名称 图形及条件 表面积 体积
长方体 S = V =
正方体 S = V =
填写下表。
(ab+ah+bh)×2
abh
6a
a
12
(1)举例说明1 cm 、1 dm 、1 m 各有多大,1 L、1 mL的水大约有多少。
答:1 cm :键盘上的1个按钮或1粒蚕豆;
1 dm :1个粉笔盒;
1 m :棱长1米的正方体箱子。
1 L的水约为两瓶矿泉水或4普通纸杯的水;
1 mL的水约为20滴。
(2)1 m = dm 700 dm = m 81 cm = mL
1 L= dm 2.3 dm = cm 560 mL= L
1000
0.7
81
1
2300
0.56
13
一块长方形铁皮(如右图),从四个角各切掉一个边长为5cm的正方形,然后做成无盖盒子。这个盒子用了多少铁皮?它的容积有多大?
表面积:30×25-5×5×4=650(cm )
容 积:(30-5×2)×(25-5×2)×5
=1500(cm )
=1500(mL)
答:这个盒子用了650cm 铁皮,它的容积有1500mL。
25cm
30cm
14
一个长方体的玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果竖直放入一块棱长为4dm的正方体铁块,缸里的水会溢出多少升?
溢出水的体积=正方体的体积-玻璃缸内没有装水部分的体积。
4×4×4-8×6×(4-2.8)=6.4(dm )=6.4(L)
答:缸里的水会溢出6.4升。
15
用4个 摆一摆。
(1)如果从左面看到的图形是 ,这4个小正方体可能是怎样摆放的?
……
(2)请你再给出从另一个方向看到的图形,让同桌猜一猜4个小正方体是怎样摆放的。
上面是
16
A
(2)这是一道开放题:可以绕底部顶点旋转,也可以绕顶部顶点旋转;可以按顺时针方向旋转,也可以按逆时针方向旋转。只要确定好旋转中心、旋转方向就可以画了。
(1)我是绕着点A按顺时针方向旋转90°的。
(1)画出“风筝”绕点A旋转90°后的图形(只画出轮廓线)。
(2)说一说你是怎样旋转并画出图形的。
17
北京2022年冬奥会和冬残奥会上,国家游泳中心“水立方”完美化身为“冰立方”,成为世界首座完成“水冰转换”的奥运场馆。作为冰壶比赛的场馆,“冰立方”改造出4条达到国际最高标准的冰壶赛道,每条赛道长44.5m,宽4.32m。由于冰壶比赛对冰面的要求非常高,所以必须经过多次细致的洒水,赛道上厚度约为80mm的冰层才能完美地呈现出来。你知道大约需要洒多少升水吗?(0.9L水可以转化为1L的冰。用计算器计算。)
44.5m=445dm 4.32m=43.2dm 80mm=0.8dm
445×43.2×0.8×4=61516.8(dm ) 61516.8×0.9=55365.12(L)
答:大约需要洒55365.12升水。
18
(1)2014—2021年全国新能源汽车销售量是怎样变化的?
2014—2021年全国新能源汽车销售量呈上升趋势。
(2)请你预测下一年全国新能源汽车的销售量。
(合理即可)我预测下一年全国新能源汽车的销售量是400万辆。
18
(3)观察折线统计图,你还能获得哪些信息?
(合理即可)2021年全国新能源汽车销售量最高。
18
19
(1)1900—2020年该地区年人均支出和年人均食品支出是怎样变化的?
年人均支出和年人均食品支出都是呈上升趋势的。
(2)观察复式折线统计图,你还能发现什么?
从1990年到2020年,年人均食品支出占当年年人均支出的比例越来越低。(合理即可)
19
算一算。
= = = =
= == =
0
1
填空。
(1)4.5=( )=( )mL
(2)650 mL =L 。
20
4500
4500
(3) 可以表示1kg的( ),也可以表示
5kg的( )。
13
2
填空。
(4)a、b是两个质数,且a×b=95,那么a+b=( )。
(5)把3kg苹果分成相等的4份,每份用分数表示是( )kg,用小数表示是( )kg,用整数表示是( )g,每份苹果的质量是总质量的,也就是1kg的。
0.75
24
750
1
4
4
3
2
简便方法计算。
3
解方程。
解:
解:
4
求下面图形的表面积和体积。(单位:cm)
10
5
6
表面积:
(5×6+10×6+5×10)×2
=140×2
=280(cm )
体积:
5×6×10
=30×10
=300(cm )
5
求下面图形的表面积和体积。(单位:cm)
表面积:
2.5
4
4
8
8
8
8×8×6
=64×6
=384(cm )
体积:
8×8×8-4×4×2.5
=512-40
=472(cm )
6
实验小学开展植树造林,绿化家园活动。五(1)班男生共植树30棵,女生共植树24棵。你能算出男、女生的植树棵数各占全班的几分之几吗?
30÷(30+24)
=30÷54
24÷(30+24)
=24÷54
=
=
答:男生植树棵数占全班的,女生植树棵数占全班的。
7
街心公园里有一个面积是公顷的圆形花圃,里面种了3种不同的花。其中牡丹占总面积的,百合占总面积的,其余的是玫瑰。你能算出玫瑰占总面积的几分之几吗?
分数不但可以表示部分与整体的关系,还可以表示具体的数量。
1
答:玫瑰占总面积的。
8
一块长方形铁皮,长32cm,在它的四个顶角分别剪去边长4cm的正方形,然后折起来焊成一个无盖的长方体铁皮盒。已知这个铁皮盒的容积是768 ,原来这块铁皮的面积是多少呢?
答:原来这块铁皮的面积是512cm 。
768÷[(32-4-4)×4]
=768÷[24×4]
=768÷96
=8(cm)
(8+4+4)×32
=16×32
=512(cm )
9
去年甲、乙两地每季度降水量如右表。
(1)请你根据表中数据制成折线统计图。
450
400
250
580
650
500
550
甲地降水量
乙地降水量
题目中有两组数据,制成复式折线统计图。
10
去年甲、乙两地每季度降水量如右表。
(2)甲地第四季度的降水量是第二季度的几分之几?
250÷650=
答:甲地第四季度的降水量是第二季度的。
10
这节课有什么收获呢?
1.观察物体
2.因数和倍数
3.长方体和正方体
4.分数的意义和性质
5.图形的运动
6.分数的加减法
7.折线统计图
8.找次品
练习二十八
1.观察物体
2.因数和倍数
3.长方体和正方体
4.分数的意义和性质
5.图形的运动
6.分数的加减法
7.折线统计图
8.找次品
练习二十八
第九单元 总复习
通过本学期的学习与复习,你学会了什么?
1.认识了因数和倍数。
2.学会了长方体和正方体表面积以及体积的计算方法,并能够运用知识解决问题。
3.学会了从不同角度观察物体,根据图形判断观察物体方向。
4.知道了分数的意义和性质,根据分数的性质进行约分、通分,能进行分数加减运算。
通过本学期的学习与复习,你学会了什么?
5.进一步加深对轴对称图形、平移以及旋转的认识。
6.认识了折线统计图,对于数据的记录,能够选择恰当的统计图进行统计。
7.学习“找次品”问题,能解决实际困难。
通过本学期的学习与复习,你学会了什么?
1
选自教材第118~121页练习二十八
下面哪些数是2的倍数?哪些是3的倍数?哪些是5的倍数?哪些是质数?哪些是合数?哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56
79
87
195
204
630
22
31
57
65
78
83
个位上是0,2,4,6或8的数都是2的倍数。
2的倍数:56、204、630、22、78;
5的倍数:195、630、65。
3的倍数:87、195、204、630、57、78;
一个数各位上的数的和是3的倍数,这个数就是3的倍数。
个位上是0或5的数都是5的倍数。
56
79
87
195
204
630
22
31
57
65
78
83
一个数,如果只有1和它本身两个因数,这样的数叫作质数。
质数:79、31、83;
奇数:79、87、195、31、57、65、83;
合数:56、87、195、204、630、22、57、65、78;
一个数,如果除了1和它本身还有别的因数,这样的数叫作合数。
整数中,是2的倍数的数叫作偶数(0也是偶数),不是2的倍数的数叫作奇数。
偶数:56、204、630、22、78。
2
(1)两个合数相乘,积还是合数。
两个合数、1和积本身都是积的因数,所以积还是合数。
判断下面的说法是否正确,并说一说你的理由。
(2)两个不同质数的公因数只有1。
(3)一个数的因数一定比它的倍数小。
正确
正确
一个数的最大因数等于它的最小倍数。
不正确
质数的因数只有1和它本身,所以两个不同质数的公因数只有1。
判断下面的说法是否正确,并说一说你的理由。
(4)两个数的最小公倍数是这两个数最大公因数的倍数。
(5)最小的质数是1。
正确
1既不是质数,也不是合数。
不正确
因为两个数的最小公倍数是其中任何一个数的倍数,两个数的最大公因数是其中任何一个数的因数,所以两个数的最小公倍数是两个数最大公因数的倍数。
2
3
找出下面每组数的最大公因数和最小公倍数,以其中一组为例,说一说你是怎样找到的。
4和5
6和16
15和20
10和8
3和9
4和5的最大公因数是1,最小公倍数是20;
6和16的最大公因数是2,最小公倍数是48;
15和20的最大公因数是5,最小公倍数是60;
10和8的最大公因数是2,最小公倍数是40;
3和9的最大公因数是3,最小公倍数是9。
求两个数的最大公因数和最小公倍数常用的方法有:列举法、筛选法、分解质因数法和短除法。
例如,
15 20
5
3
4
15和20的最大公因数是5,最小公倍数是5×3×4=60。
用公有的质因数连续去除
除到两个数的商是互质数为止
所有除数的积
所有除数和商的积
4
食品店有70多个松花蛋。如果把它们装进4个一排的蛋托中,正好装完;如果把它装进6个一排的蛋托中,也正好装完。一共有多少个松花蛋?
答:一共有72个松花蛋。
4和6的公倍数有:12,24,36,48,60,72,84……
已知食品店有70多个松花蛋,所以应该有72个松花蛋。
5
(1)把 4 m长的绳子平均剪成5段,每段长 m,
每段绳子是全长的 。
(2)1985 年第二次大熊猫调查结果显示,全国共有1114只野生大熊猫。2015 年第四次大熊猫调查结果显示,
5
4
5
1
全国共有1864只野生大熊猫,其中1387只生活在四川。第二次调查到的野生大熊猫数量是第四次调查数量的 ;根据第四次调查,生活在四川的野生大熊猫占所有野生大熊猫数量的 。
932
557
1864
1387
0
1
2
3
4
6
用直线上的点表示下面各数,哪个数最接近 2?
1.5
3
1
4
5
1. 5
3
1
8
17
4
5
5
3
5
3
2
10
13
3.7
2.8
3. 7
8
17
2. 8
5
3
10
13
8
17
最接近 2。
5
3
2
7
先填空,再把各数按从小到大的顺序排列起来。
2
7
=
( )
21
9
12
=
3
( )
5÷3= =1
( )
( )
( )
( )
2=
( )
( )
6
4
5
3
2
3
2
1
2
7
< <5÷3<2
9
12
8
下列分数中哪些是最简分数?把不是最简分数的化成最简分数,并说一说化简的依据。
6
8
36
16
10
21
30
45
12
25
5
7
72
6
最简分数有: 、 、 。其余的都不是最简分数,
根据分数的基本性质化简分数:
10
21
12
25
5
7
6
8
=
3
4
36
16
=
9
4
30
45
=
2
3
72
6
=12
9
计算。
10
3
+
10
7
=
10
10
= 1
6
5
-
6
1
=
6
4
=
3
2
7
4
-
3
1
=
21
12
-
21
7
=
21
5
6
1
5
1
2
1
+
+
=
30
5
+
30
6
+
30
15
=
30
26
=
15
13
计算。
8
7
-
4
3
=
8
7
-
8
6
=
8
1
3
2
+
9
7
=
9
6
+
9
7
=
9
13
7
-
3
5
=
3
21
-
3
5
=
3
16
6
-( - )
4
3
5
2
=
20
120
-( )
20
15
-
20
8
=
20
120
-
20
7
=
20
113
9
10
中国煤炭资源的种类较多,具体构成如右图。
(1)褐煤占煤炭总量的几分之几?
(2)你还能提出其他数学问题并解答吗?
(1)1- - =
3
4
3
25
13
100
答:褐煤占煤炭总量的 。
13
100
10
中国煤炭资源的种类较多,具体构成如右图。
(1)褐煤占煤炭总量的几分之几?
(2)你还能提出其他数学问题并解答吗?
(2)参考答案:
问:烟煤比无烟煤多占煤炭总量的几分之几?
- =
3
4
3
25
63
100
答:烟煤比无烟煤多占煤炭总量的 。
63
100
11
名称 图形及条件 表面积 体积
长方体 S = V =
正方体 S = V =
填写下表。
(ab+ah+bh)×2
abh
6a
a
12
(1)举例说明1 cm 、1 dm 、1 m 各有多大,1 L、1 mL的水大约有多少。
答:1 cm :键盘上的1个按钮或1粒蚕豆;
1 dm :1个粉笔盒;
1 m :棱长1米的正方体箱子。
1 L的水约为两瓶矿泉水或4普通纸杯的水;
1 mL的水约为20滴。
(2)1 m = dm 700 dm = m 81 cm = mL
1 L= dm 2.3 dm = cm 560 mL= L
1000
0.7
81
1
2300
0.56
13
一块长方形铁皮(如右图),从四个角各切掉一个边长为5cm的正方形,然后做成无盖盒子。这个盒子用了多少铁皮?它的容积有多大?
表面积:30×25-5×5×4=650(cm )
容 积:(30-5×2)×(25-5×2)×5
=1500(cm )
=1500(mL)
答:这个盒子用了650cm 铁皮,它的容积有1500mL。
25cm
30cm
14
一个长方体的玻璃缸,长8dm,宽6dm,高4dm,水深2.8dm。如果竖直放入一块棱长为4dm的正方体铁块,缸里的水会溢出多少升?
溢出水的体积=正方体的体积-玻璃缸内没有装水部分的体积。
4×4×4-8×6×(4-2.8)=6.4(dm )=6.4(L)
答:缸里的水会溢出6.4升。
15
用4个 摆一摆。
(1)如果从左面看到的图形是 ,这4个小正方体可能是怎样摆放的?
……
(2)请你再给出从另一个方向看到的图形,让同桌猜一猜4个小正方体是怎样摆放的。
上面是
16
A
(2)这是一道开放题:可以绕底部顶点旋转,也可以绕顶部顶点旋转;可以按顺时针方向旋转,也可以按逆时针方向旋转。只要确定好旋转中心、旋转方向就可以画了。
(1)我是绕着点A按顺时针方向旋转90°的。
(1)画出“风筝”绕点A旋转90°后的图形(只画出轮廓线)。
(2)说一说你是怎样旋转并画出图形的。
17
北京2022年冬奥会和冬残奥会上,国家游泳中心“水立方”完美化身为“冰立方”,成为世界首座完成“水冰转换”的奥运场馆。作为冰壶比赛的场馆,“冰立方”改造出4条达到国际最高标准的冰壶赛道,每条赛道长44.5m,宽4.32m。由于冰壶比赛对冰面的要求非常高,所以必须经过多次细致的洒水,赛道上厚度约为80mm的冰层才能完美地呈现出来。你知道大约需要洒多少升水吗?(0.9L水可以转化为1L的冰。用计算器计算。)
44.5m=445dm 4.32m=43.2dm 80mm=0.8dm
445×43.2×0.8×4=61516.8(dm ) 61516.8×0.9=55365.12(L)
答:大约需要洒55365.12升水。
18
(1)2014—2021年全国新能源汽车销售量是怎样变化的?
2014—2021年全国新能源汽车销售量呈上升趋势。
(2)请你预测下一年全国新能源汽车的销售量。
(合理即可)我预测下一年全国新能源汽车的销售量是400万辆。
18
(3)观察折线统计图,你还能获得哪些信息?
(合理即可)2021年全国新能源汽车销售量最高。
18
19
(1)1900—2020年该地区年人均支出和年人均食品支出是怎样变化的?
年人均支出和年人均食品支出都是呈上升趋势的。
(2)观察复式折线统计图,你还能发现什么?
从1990年到2020年,年人均食品支出占当年年人均支出的比例越来越低。(合理即可)
19
算一算。
= = = =
= == =
0
1
填空。
(1)4.5=( )=( )mL
(2)650 mL =L 。
20
4500
4500
(3) 可以表示1kg的( ),也可以表示
5kg的( )。
13
2
填空。
(4)a、b是两个质数,且a×b=95,那么a+b=( )。
(5)把3kg苹果分成相等的4份,每份用分数表示是( )kg,用小数表示是( )kg,用整数表示是( )g,每份苹果的质量是总质量的,也就是1kg的。
0.75
24
750
1
4
4
3
2
简便方法计算。
3
解方程。
解:
解:
4
求下面图形的表面积和体积。(单位:cm)
10
5
6
表面积:
(5×6+10×6+5×10)×2
=140×2
=280(cm )
体积:
5×6×10
=30×10
=300(cm )
5
求下面图形的表面积和体积。(单位:cm)
表面积:
2.5
4
4
8
8
8
8×8×6
=64×6
=384(cm )
体积:
8×8×8-4×4×2.5
=512-40
=472(cm )
6
实验小学开展植树造林,绿化家园活动。五(1)班男生共植树30棵,女生共植树24棵。你能算出男、女生的植树棵数各占全班的几分之几吗?
30÷(30+24)
=30÷54
24÷(30+24)
=24÷54
=
=
答:男生植树棵数占全班的,女生植树棵数占全班的。
7
街心公园里有一个面积是公顷的圆形花圃,里面种了3种不同的花。其中牡丹占总面积的,百合占总面积的,其余的是玫瑰。你能算出玫瑰占总面积的几分之几吗?
分数不但可以表示部分与整体的关系,还可以表示具体的数量。
1
答:玫瑰占总面积的。
8
一块长方形铁皮,长32cm,在它的四个顶角分别剪去边长4cm的正方形,然后折起来焊成一个无盖的长方体铁皮盒。已知这个铁皮盒的容积是768 ,原来这块铁皮的面积是多少呢?
答:原来这块铁皮的面积是512cm 。
768÷[(32-4-4)×4]
=768÷[24×4]
=768÷96
=8(cm)
(8+4+4)×32
=16×32
=512(cm )
9
去年甲、乙两地每季度降水量如右表。
(1)请你根据表中数据制成折线统计图。
450
400
250
580
650
500
550
甲地降水量
乙地降水量
题目中有两组数据,制成复式折线统计图。
10
去年甲、乙两地每季度降水量如右表。
(2)甲地第四季度的降水量是第二季度的几分之几?
250÷650=
答:甲地第四季度的降水量是第二季度的。
10
这节课有什么收获呢?
1.观察物体
2.因数和倍数
3.长方体和正方体
4.分数的意义和性质
5.图形的运动
6.分数的加减法
7.折线统计图
8.找次品
练习二十八
1.观察物体
2.因数和倍数
3.长方体和正方体
4.分数的意义和性质
5.图形的运动
6.分数的加减法
7.折线统计图
8.找次品
