16.3 分式方程
图片预览





文档简介
课件18张PPT。16.3 分式方程 学习目标:
1、掌握分式方程的概念;
2、理解分式方程的解题思路;
3、初步掌握解分式方程的一般步骤;
4、了解分式方程产生增根的原因及掌握验根的方法。让我们携手共同去探究吧!数学来源于生活 尹老师今年的年龄与9的差除以她年龄与9的和的商等于—,请同学们猜猜尹老师的年龄。解 :设尹老师的年龄为 x 岁, 列方程得12生活中的数学 概括:
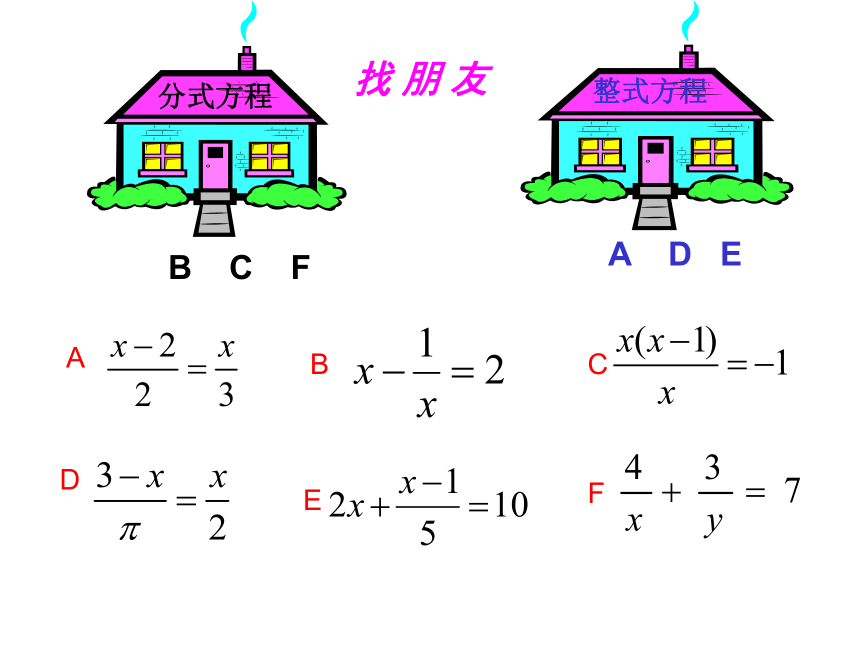
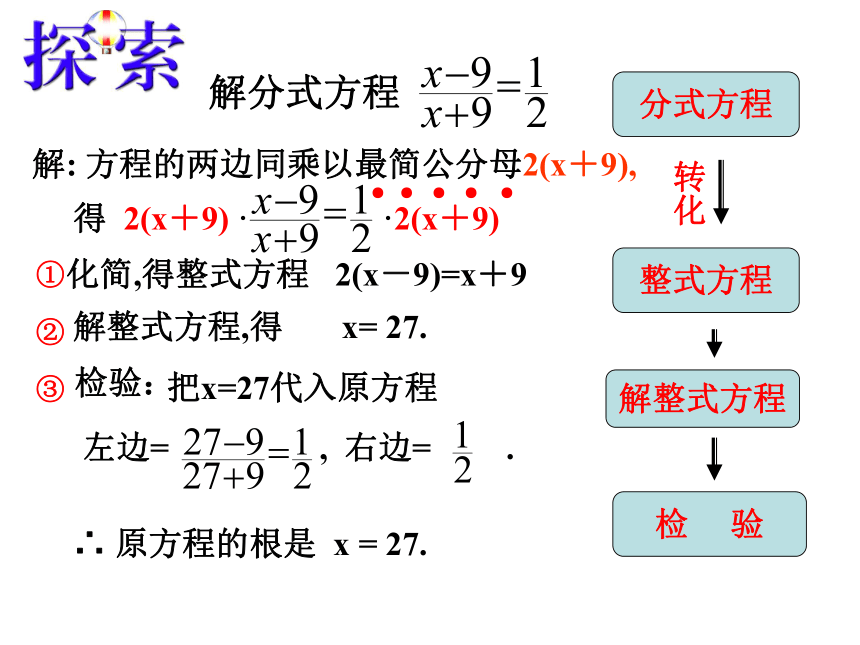
分母中含有未知数的方程,叫做分式方程此方程有何特征?议一议 找 朋 友A BCDEFB C FA D E解分式方程 化简,得整式方程 2(x-9)=x+9解整式方程,得 x= 27. 把x=27代入原方程
左边= , 右边= .∴ 原方程的根是 x = 27.● ● ● ● ●分式方程整式方程解整式方程检 验转化① ② ③检验:得 2(x+9) · ·2(x+9)试一试增根的定义因此解分式方程可能产生增根,解分式方程必须检验 ( 代入最简公分母检验)例1 解方程解:方程两边同乘以最简公分母 x(x-3),
化简,得 2x=3(x-3)
解得 x=9,
检验: 把x=9, 代入最简公分母,
x(x-3)= 54 ≠0
∴原方程的根是x= 9.
例2 解方程解:方程两边同乘以最简公分母 2(x-1)
解得 x= ,
检验: 把x= 代入最简公分母,
2(x-1)= ≠0
∴ 原方程的根是 x =
作 业 1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.一化二解三检验解分式方程的一般步骤智力大比拼争学习力努取步进 1. 认识了分式方程
2. 解分式方程的一般步骤你有哪些收获?作 业:1. 书: 习题16.3
第一题
2. 轻巧夺冠
3. 预习新课谢谢指导!1. 分式方程 的最简公分母是 .X-14.下列方程中,不是分式方程的是( )2.分式方程的特征是什么?对分式方程的根检验的方法有那些?3.如果 增根,那么增根为 .X=2C争取进步X=3X = - 4X=4X= 3 / 4
1、掌握分式方程的概念;
2、理解分式方程的解题思路;
3、初步掌握解分式方程的一般步骤;
4、了解分式方程产生增根的原因及掌握验根的方法。让我们携手共同去探究吧!数学来源于生活 尹老师今年的年龄与9的差除以她年龄与9的和的商等于—,请同学们猜猜尹老师的年龄。解 :设尹老师的年龄为 x 岁, 列方程得12生活中的数学 概括:
分母中含有未知数的方程,叫做分式方程此方程有何特征?议一议 找 朋 友A BCDEFB C FA D E解分式方程 化简,得整式方程 2(x-9)=x+9解整式方程,得 x= 27. 把x=27代入原方程
左边= , 右边= .∴ 原方程的根是 x = 27.● ● ● ● ●分式方程整式方程解整式方程检 验转化① ② ③检验:得 2(x+9) · ·2(x+9)试一试增根的定义因此解分式方程可能产生增根,解分式方程必须检验 ( 代入最简公分母检验)例1 解方程解:方程两边同乘以最简公分母 x(x-3),
化简,得 2x=3(x-3)
解得 x=9,
检验: 把x=9, 代入最简公分母,
x(x-3)= 54 ≠0
∴原方程的根是x= 9.
例2 解方程解:方程两边同乘以最简公分母 2(x-1)
解得 x= ,
检验: 把x= 代入最简公分母,
2(x-1)= ≠0
∴ 原方程的根是 x =
作 业 1.在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2.解这个整式方程.
3.把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解,必须舍去.
4、写出原方程的根.一化二解三检验解分式方程的一般步骤智力大比拼争学习力努取步进 1. 认识了分式方程
2. 解分式方程的一般步骤你有哪些收获?作 业:1. 书: 习题16.3
第一题
2. 轻巧夺冠
3. 预习新课谢谢指导!1. 分式方程 的最简公分母是 .X-14.下列方程中,不是分式方程的是( )2.分式方程的特征是什么?对分式方程的根检验的方法有那些?3.如果 增根,那么增根为 .X=2C争取进步X=3X = - 4X=4X= 3 / 4
